Review of Energy Units

Before going ahead, we need to make sure we all have a clear picture of the various units we use to measure energy.

Joule — the joule (J) is the basic unit of energy, work done, or heat in the SI system of units; it is defined as the amount of energy, or work done, in applying a force of one Newton over a distance of one meter. One way to think of this is as the energy needed to lift a small apple (about 100 g) one meter. An average person gives off about 60 J per second in the form of heat. We are going to be talking about very large amounts of energy, so we need to know about some terms that are used to describe larger sums of energy:

In recent years, we humans have consumed about 518 EJ of energy per year, which is something like 74 GJ per person per year.

British Thermal Unit— the btu is another unit of energy that you might run into. One btu is the amount of energy needed to warm one pound of water one °F. One btu is equal to about 1055 joules of energy. Oddly, some branches of our government still use the btu as a measure of energy.

Watt— the watt (W) is a measure of power and is closely related to the Joule; it is the rate of energy flow, or joules/second. For instance, a 40 W light bulb uses 40 joules of energy per second, and the average sunlight on the surface of Earth delivers 343 W over every square meter of the surface.

Kilowatt hours— when you (or you parents maybe for now) pay the electric bill each month, you get charged according to how much energy you used, and they express this in the form of kilowatt hours — kWh. If you use 1000 Watts for one hour, then you have used one kWh. This is really a unit of energy, not power:

$$\text{1[kWh]=1000[W]}\times \text{1[hr]=1000}\left[\frac{J}{s}\right]\times \text{3600[s]=3,600,000[J]}$$

In other words, one kilowatt hour is 1000 joules per second (kW) summed up over one hour (3600 seconds), which is the same as 3.6 MJ or 3.6 x 10⁶J or 3.6e6 J.

Global Energy Sources

The energy we use to support the whole range of human activities comes from a variety of sources, but as you all know, fossil fuels (coal, oil, and natural gas) currently provide the majority of our energy on a global basis, supplying about 81% of the energy we use:

Figure 1. The current contributions to our global energy from different sources shows that fossil fuels account for 81% of our energy. Data from International Energy Agency (iea.org)

Click for a text description of the Sources of Global Energy chart.

The image is a pie chart titled "Sources of Global Energy," showing the distribution of different energy sources globally. The chart is divided into segments, each representing a different energy source with corresponding percentages:

• Oil: The largest segment, colored in blue, represents 33% of global energy sources.
• Coal: The second largest segment, colored in red, accounts for 27% of global energy.
• Gas: Represented by a green segment, gas makes up 21% of the energy mix.
• Solar, Wind, Other: This segment is yellow and constitutes 11% of the energy sources.
• Hydro: A light blue segment representing 2% of global energy.
• Nuclear: The smallest segment, colored in purple, accounts for 6% of the energy sources.

Each segment is labeled with the energy source and its percentage, providing a clear breakdown of the global energy composition.

Credit: David Bice @ Penn State is licensed under CC-BY-NC-4.0

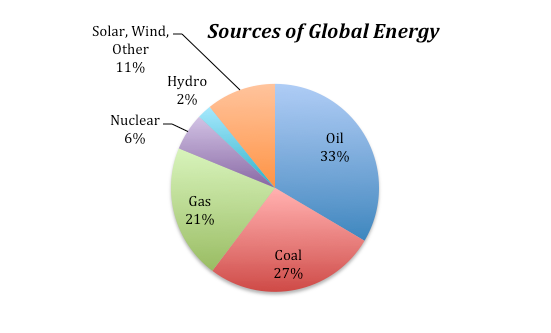
The non-fossil fuel sources include nuclear, hydro (dams with electrical turbines attached to the outflow), solar (both photovoltaic and solar thermal), and a variety of other sources. These non-fossil fuel sources currently supply about 19% of the total energy.

The percentages of our energy provided by these different sources have clearly changed over time and will certainly change in the future as well. The graph below gives us some sense of how dramatically things have changed over the past 210 years:

Figure 2. This plot shows the history of global energy production from different sources. Note that as time goes on, we are getting our energy from more sources. Data from Smil (2010).

Click for a text description of the Global Energy Consumption by Source graph.

The image is a line graph titled "Global Energy Consumption by Source," showing the consumption of various energy sources from the year 1800 to 2000. The y-axis represents energy consumption in exajoules (EJ), ranging from 0 to 160 EJ. The x-axis represents the years, marked at intervals from 1800 to 2000.

The graph includes data for five different energy sources, each represented by a different colored line:

• Biofuels: Represented by a light blue line, biofuel consumption starts at around 10 EJ in 1800 and shows a slight increase over time, peaking around 20 EJ by 2000.
• Coal: Represented by a red line, coal consumption starts near 0 EJ in 1800, begins to rise significantly around 1850, and continues to increase sharply, reaching approximately 120 EJ by 2000.
• Crude Oil: Represented by a green line, crude oil consumption starts near 0 EJ in 1850, increases steadily from around 1900, and rises sharply post-1950, reaching about 140 EJ by 2000.
• Natural Gas: Represented by a purple line, natural gas consumption starts near 0 EJ in 1900, with a notable increase starting around 1950, reaching around 100 EJ by 2000.
• Hydro Electricity: Represented by a dark blue line, hydroelectricity consumption starts near 0 EJ around 1900, with a gradual increase over time, reaching about 30 EJ by 2000.
• Nuclear Electricity: Represented by an orange line, nuclear electricity consumption starts near 0 EJ around 1950, with a sharp increase from that point, reaching around 30 EJ by 2000.

Key observations:

• Coal and crude oil show the most significant increases in consumption over the period.
• Natural gas consumption also rises sharply, particularly after 1950.
• Biofuels show a relatively flat trend, with a minor increase.
• Hydro and nuclear electricity consumption start later, but show steady growth over time.
• By 2000, crude oil has the highest consumption, followed by coal, natural gas, hydroelectricity, nuclear electricity, and biofuels in that order.

A legend in the top-left corner of the graph identifies the colors associated with each energy source.

Credit: David Bice @ Penn State is licensed under CC-BY-NC-4.0

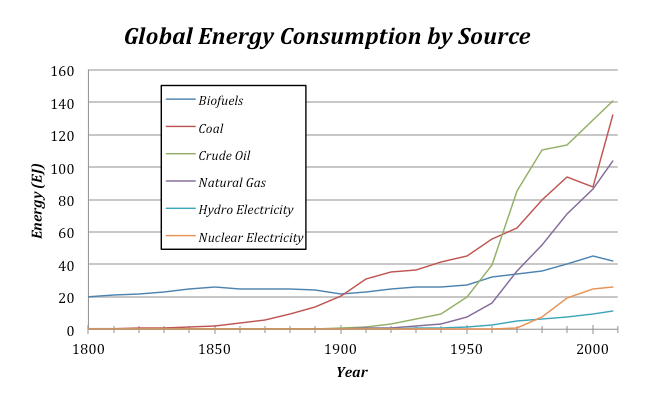
There are a couple of interesting features to point out about this graph. For one, note that the total amount of energy consumed has risen dramatically over time — this is undoubtedly related to both population growth and the industrial revolution. The second point is that shifting from one energy source to another takes a long time. Oil was being pumped out of the ground in 1860, and even though it has a greater energy density and is more versatile than coal, it did not really make its mark as an energy source until about 1920, and it did not surpass coal as an energy source until about 1940. Of course, you might argue that the world changed more slowly back then, but it is probably hard to avoid the conclusion that our energy supply system has a lot of inertia, resulting in sluggish change.

Global Energy Uses

We are all aware of some of the ways we use energy — heating and cooling our homes, transporting ourselves via car, bus, train, or plane — but there are many other uses of energy that we tend not to think about. For instance, growing food and getting it onto your plate uses energy — think of the farming equipment, the food processing plant, the transportation to your local store. Or, think of manufactured items — to make something like a car requires energy to extract the raw materials from the earth and then assembling them requires a great deal of energy. So, when you consider all of the different uses of energy, we see a dominance of industrial uses:

Figure 3. Most of our energy is used in industrial applications, mainly in the form of electricity. We are generally the most aware of our use of energy in transportation because we pay for it on a regular basis. Data from International Energy Agency (iea.org)

Click for a text description of the Global Energy End Use chart.

The image is a pie chart titled "Global Energy End Use," showing the distribution of global energy consumption across different sectors. The chart is divided into four segments, each representing a different sector with corresponding percentages:

• Industry: The largest segment, colored in blue, represents 52% of global energy end use.
• Transport: The second largest segment, colored in red, accounts for 26% of the energy consumption.
• Residential: Represented by a purple segment, this sector uses 14% of the global energy.
• Commercial: The smallest segment, colored in green, constitutes 8% of the energy end use.

Each segment is labeled with the sector name and its percentage, providing a clear breakdown of how global energy is utilized across these sectors.

Credit: David Bice @ Penn State is licensed under CC-BY-NC-4.0

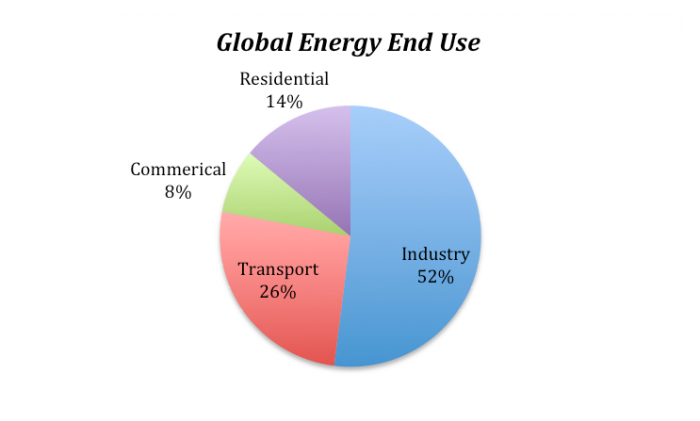
Global Energy Consumption

Since we are going to be modeling the future of global energy consumption, we should first familiarize ourselves with the recent history of energy consumption.

Figure 4. This plot shows the history of global energy production from different sources. Note that as time goes on, we are getting our energy from more sources. Data from Smil (2010).

Click for a text description of the History of Global Energy Consumption graph.

The image is a stacked area chart titled "History of Global Energy Consumption," showing the consumption of various energy sources from 1800 to 2000. The y-axis represents energy consumption in exajoules (EJ), ranging from 0 to 500 EJ. The x-axis represents the years, marked at intervals from 1800 to 2000.

The chart includes data for six different energy sources, each represented by a different colored area:

• Biofuels: Represented by a red area at the bottom of the stack, biofuel consumption starts at around 10 EJ in 1800 and shows a gradual increase, peaking around 50 EJ by 2000.
• Coal: Represented by a green area above biofuels, coal consumption starts near 0 EJ in 1800, begins to rise significantly around 1850, and continues to increase sharply, reaching approximately 150 EJ by 2000.
• Crude Oil: Represented by a yellow area above coal, crude oil consumption starts near 0 EJ around 1880, with a notable increase starting around 1900, reaching about 150 EJ by 2000.
• Natural Gas: Represented by a light blue area above crude oil, natural gas consumption starts near 0 EJ around 1900, with a sharp increase post-1950, reaching around 100 EJ by 2000.
• Hydro Electricity: Represented by an orange area above natural gas, hydro electricity consumption starts near 0 EJ around 1900, with a steady increase over time, reaching about 30 EJ by 2000.
• Nuclear Electricity: Represented by a dark blue area at the top, nuclear electricity consumption starts near 0 EJ around 1950, with a rapid increase from that point, reaching around 30 EJ by 2000.

Key observations:

• The total energy consumption shows a steep rise starting around the mid-20th century.
• Coal and crude oil have the largest contributions to the total energy consumption, especially from the late 19th century onwards.
• Natural gas becomes significant post-1950.
• Hydro and nuclear electricity start later but show steady growth.
• Biofuels have a consistent but smaller share throughout the period.

A legend on the right side of the chart identifies the colors associated with each energy source.

Credit: David Bice @ Penn State is licensed under CC-BY-NC-4.0

Question: Why has our energy consumption increased over this time period?

Here, we will explore a few possibilities, the first of which is global population increase — more people on the planet leads to a greater total energy consumption. To evaluate this, we need to plot the global population and the total energy consumption on the same graph to see if the rise in population matches the rise in energy consumption.

Figure 5. Data from Smil (2010), and UN (population).

Click for a text description of the Energy Consumption and Population graph.

The image is a line graph titled "Energy Consumption and Population," showing the relationship between global energy consumption and global population from the year 1800 to 2000.

• Axes:
  • The x-axis represents the years, ranging from 1800 to 2000.
  • The left y-axis represents energy consumption in exajoules (EJ), ranging from 0 to 500 EJ.
  • The right y-axis represents population in billions, ranging from 0.800 to 6.800 billion


• Data Series:
  • Energy Consumption: Represented by blue squares connected by a line, this series shows the trend of global energy consumption over time. It starts at a low level around 10 EJ in 1800 and increases steadily, with a significant rise starting around 1950, reaching approximately 450 EJ by 2000.
  • Population: Represented by red circles connected by a line, this series shows the trend of global population growth. It starts at around 1 billion in 1800 and grows gradually, with a sharp increase post-1950, reaching about 6.8 billion by 2000
• Trends:
  • Both energy consumption and population show a similar trend of gradual increase until around 1950, after which both exhibit exponential growth.
  • The correlation between the two trends is evident, with both lines rising sharply in the latter half of the 20th century, indicating a strong relationship between population growth and energy consumption


• Key Points:
  • Around 1800, energy consumption is very low, and the population is just above 1 billion.
  • By 1900, energy consumption has risen to about 30 EJ, and the population has grown to approximately 1.6 billion.
  • Post-1950, there is a dramatic increase in both metrics, with energy consumption reaching nearly 450 EJ and the population reaching 6.8 billion by 2000

The graph uses two different scales to represent energy consumption and population, with the right y-axis for population being in billions and the left y-axis for energy consumption being in exajoules. The visual representation highlights the parallel growth of these two variables over the 200-year period.

Credit: David Bice @ Penn State is licensed under CC-BY-NC-4.0

The two curves match very closely, suggesting that population increase is certainly one of the main reasons for the rise in energy consumption. But is it as simple as that — more people equals more energy consumption?

If the rise in global energy consumption is due entirely to population increase, then there should be a constant amount of energy consumed per person — this is called the per capita energy consumption. To get the per capita energy consumption, we just need to divide the total energy by the population (in billions) — so we’ll end up with Exajoules of energy per billion people.

Figure 6. The globally averaged per capita energy consumption, broken down by energy source. Data from Smil (2010), and UN (population).

Click for a text description of the History of Per Capita Energy Consumption graph.

The image is a stacked area chart titled "History of Per Capita Energy Consumption," showing the consumption of various energy sources per capita from 1800 to 2000. The y-axis represents energy consumption in exajoules per billion people, ranging from 0 to 80 EJ per billion. The x-axis represents the years, marked at intervals from 1800 to 2000.

The chart includes data for six different energy sources, each represented by a different colored area:

• Biofuels: Represented by a red area at the bottom of the stack, biofuel consumption starts at around 10 EJ per billion in 1800 and shows a gradual increase, peaking around 20 EJ per billion by the mid-20th century before declining slightly towards 2000.
• Coal: Represented by a green area above biofuels, coal consumption starts near 0 EJ per billion in 1800, begins to rise significantly around 1850, and continues to increase, reaching a peak of about 30 EJ per billion around 1950, then declines slightly but remains significant.
• Crude Oil: Represented by a purple area above coal, crude oil consumption starts near 0 EJ per billion around 1880, with a notable increase starting around 1900, reaching about 30 EJ per billion by 1970, then slightly decreases.
• Natural Gas: Represented by a light blue area above crude oil, natural gas consumption starts near 0 EJ per billion around 1900, with a sharp increase post-1950, reaching around 20 EJ per billion by 2000.
• Hydro: Represented by an orange area above natural gas, hydro energy consumption starts near 0 EJ per billion around 1900, with a steady increase over time, reaching about 10 EJ per billion by 2000.
• Nuclear Electricity: Represented by a dark blue area at the top, nuclear electricity consumption starts near 0 EJ per billion around 1950, with a rapid increase from that point, reaching around 10 EJ per billion by 2000.

Key observations:

• The total per capita energy consumption shows a steady increase from 1800, with a significant rise starting around the mid-20th century.
• Coal and crude oil have significant contributions to per capita energy consumption, especially from the late 19th century onwards.
• Natural gas becomes a major contributor post-1950.
• Hydro and nuclear electricity start later but show steady growth, becoming more prominent towards the end of the 20th century.
• Biofuels have a consistent but decreasing share towards the end of the period.

A legend on the right side of the chart identifies the colors associated with each energy source.

Credit: David Bice @ Penn State is licensed under CC-BY-NC-4.0

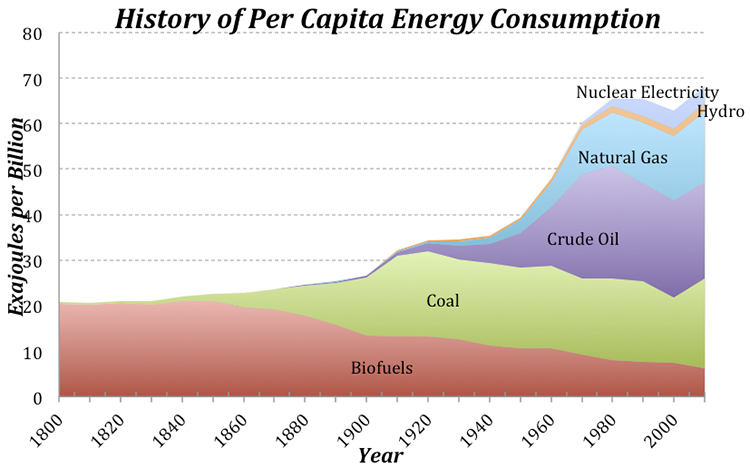
Today, we use about 3 times as much energy per person than in 1900, which is not such a surprise if you consider that we have many more sources of energy available to us now compared to 1900. Note that at the same time that the population really takes off (see Fig. 5), the per capita energy consumption also begins to rise. This means that the total global energy consumption rises due to both the population and the demand per person for more energy.

Let’s try to understand this per capita energy consumption a bit better. We know that the global average is 74 EJ per billion people, but how does this value change from place to place? There are some huge variations across the globe — Afghans use about 4 GJ per person per year, while Icelanders use 709 GJ per person. Why does it vary so much? Is it due to the level of economic development, or the availability of energy, or the culture, or the climate? You can come up with reasons why each of these factors (and others) might be important, but let’s examine one in more detail — the economic development expressed as the GDP (the gross domestic product, which reflects the size of the economy) per capita.

Figure 7. The per capita energy as a function of the per capita GDP. The axes of this plot are not linear, but logarithmic in order to show more clearly what is going on at the lower values. If you plot this with linear axes, the data mostly form a big cloud in the lower left. The red squares show the global averages in 2013 and about 1950. Data World Bank.

Click for a text description of Relationship Between GDP and Energy Consumption.

The image is a scatter plot graph titled "Relationship Between GDP and Energy Consumption." It illustrates the relationship between per capita GDP (in $) on the x-axis and per capita energy consumption (in GJ/person) on the y-axis for various countries over time. The graph uses a logarithmic scale for both axes.

• Axes:
  • The x-axis is labeled "Per Capita GDP $" and ranges from 1,000 to 100,000.
  • The y-axis is labeled "Per Capita Energy Consumption (GJ/person)" and ranges from 1 to 1,000.
• Data Points:
  • Each data point represents a country, with blue circles indicating data from various years.
  • Specific countries are highlighted with labels:
    • Afghanistan is located at the lower left of the graph, indicating low GDP and low energy consumption.
    • Mexico is positioned towards the middle of the graph.
    • USA is located towards the upper right, indicating higher GDP and energy consumption.
    • Qatar and Iceland are at the far right, with very high GDP and energy consumption, with Iceland having the highest energy consumption
  • Global Averages:
    • Two red squares mark the global averages:
      • One labeled "Global Average 1950" is located lower on the graph, indicating lower GDP and energy consumption.
      • Another labeled "Global Average 2013" is positioned higher, showing an increase in both GDP and energy consumption over time.
    • Trends:
      • There is a general upward trend, suggesting that as per capita GDP increases, so does per capita energy consumption.
      • The spread of data points widens as GDP increases, indicating variability in energy consumption among countries with similar GDP levels.
    • Annotations:
      • Arrows point to the labeled countries and global averages, providing a visual guide to their positions on the graph.

      The graph uses a logarithmic scale to accommodate the wide range of values, and the data points are densely packed, showing the distribution and relationship between GDP and energy consumption across different countries.

Credit: David Bice @ Penn State is licensed under CC-BY-NC-4.0

The obvious linear trend to these data suggests that per capita energy consumption is a function of GDP, while the fact that it is not a tight line tells us that GDP is not the whole story in terms of explaining the differences in energy consumption. Not surprisingly, we are near the upper right of this plot, consuming more than 300 GJ per person per year. Iceland’s economy is not as big per person as ours, and yet they consume vast amounts of energy per person, partly because it is cold and they have big heating demands, but also because they have abundant, inexpensive geothermal energy thanks to the fact that they live on a huge volcano. Many European countries with strong economies (e.g., Germany) use far less energy per person than we do (168 GJ compared to our 301 GJ), in part because they are more efficient than us and in part because they are smaller, which cuts down on their transportation. A big part of the reason they are more efficient than us is that energy costs more over there — for instance, a gallon of gas in Italy is about $8. Our neighbor, Mexico, has a per capita energy consumption that is just about the global average.

Pay attention to the two red squares in Fig. 7 — these show the global averages in terms of GDP and energy consumption per person for two points in time. The trend is most definitely towards increasing GDP (meaning increasing economic development) and increasing energy consumption per person. Economic development is definitely a good thing because it is tied to all sorts of indicators of a higher quality of life — better education, better health care, better diet, increased life expectancy, and lower birth rates. But, economic growth has historically come with higher energy consumption, and that means higher carbon emissions.

Now that we’ve seen what some of the patterns and trends are, we are ready to think about the future.

Creating an Emissions Scenario

There are many ways to meet our energy demands for the future, and each way could include different choices about how much of each energy source we will need. We’re going to refer to these “ways” as scenarios — hypothetical descriptions of our energy future. Each scenario could also include assumptions about how the population will change, how the economy will grow, how much effort we put into developing new technologies and conservation strategies. Each scenario can be used to generate a history of emissions of CO₂, and then we can plug that into a climate model to see the consequences of each scenario.

Emissions per unit energy for different sources

The global emission of carbon into the atmosphere due to human activities is dominated by the combustion of fossil fuels in the generation of energy, but the various energy sources — coal, oil, and gas — emit different amounts of CO₂ per unit of energy generated. Coal releases the most CO₂per unit of energy generated during combustion — about 103.7 g CO₂per MJ (10⁶ J) of energy. Oil follows with 65.7 g CO₂/MJ, and gas is the “cleanest” or most efficient of these, releasing about 62.2 g CO₂/MJ.

At first, you might think that renewable or non-fossil fuel sources of energy will not generate any carbon emissions, but in reality, there are some emissions related to obtaining our energy from these means. For example, a nuclear power plant requires huge quantities of cement, the production of which releases CO₂ into the atmosphere. The manufacture of solar panels requires energy as well, and so there are emissions related to that process because our current industrial world gets most of its energy from fossil fuels. For these energy sources, the emissions per unit of energy are generally estimated using a lifetime approach — if you emitted 1000 g of CO₂ to make a solar panel and over its lifetime, it generated 500 MJ, then its emission rate is 2 g CO₂/MJ. If we average these non-fossil fuel sources together, they release about 5 g CO₂/MJ — far cleaner than the other energy sources, but not perfectly clean.

So, to sum it up, here is a ranking of the emissions related to different energy sources:

*Hydro, Nuclear, Wind, Solar

**This will decrease as the non-fossil fuel fraction increases

Calculating global emissions of carbon

Our recent energy consumption is about 518 EJ (10¹⁸ J). Let’s calculate the emissions of CO₂ caused by this energy consumption, given the values for CO₂/MJ given above and the current proportions of energy sources — 33% oil, 27% coal, 21% gas, and 19% other non-fossil fuel sources. The way to do this is to first figure out how many grams of CO₂ are emitted per MJ given this mix of fuel sources, and then scale up from 1 MJ to 518 EJ. Let’s look at an example of how to do the math here — let r_1-4 in the equation below be the rates of CO₂ emission per MJ given above, and let f_1-4 be the fractions of different fuels given above. So r₁ could be the rate for oil (65.7) and f₁ would be the fraction of oil (.33). You can get the composite rate from:

$$r_c=r_1{f}_1+r_2{f}_2+r_3{f}_3+r_4{f}_4$$

Plugging in the numbers, we get:

$$65.7\times .33+62.2\times .27+103.7\times .21+6.2\times .19=61.4\left[\frac{{\mathrm{gCo}}_2}{\mathrm{MJ}}\right]$$

What is the total amount of CO₂ emitted? We want the answer to be in Gigatons — that’s a billion tons, and in the metric system, one ton is 1000 kg (1e6 g or 10⁶ g), which means that 1Gt = 10¹⁵ g (1e15 g).

$$1[\mathrm{EJ}]=1\mathrm{e}12[\mathrm{MJ}],\text{so},518[\mathrm{EJ}]=518\mathrm{e}12[\mathrm{MJ}]$$

$$518\mathrm{e}12[\mathrm{MJ}]\times 61.4\left[\frac{{\mathrm{gCO}}_2}{\mathrm{MJ}}\right]=31.7\mathrm{e}15\left[{\mathrm{gCO}}_2\right]=31.8$$

So, the result is 31.8 Gt of CO₂, which is very close to recent estimates for global emissions.

It is more common to see the emissions expressed as Gt of just C, not CO₂, and we can easily convert the above by multiplying it by the atomic weight of carbon divided by the molecular weight of CO₂, as follows:

$$31.8\left[{\mathrm{GtCO}}_2\right]\times \frac{12[\mathrm{gC}]}{44\left[{\mathrm{gCO}}_2\right]}=8.7[\mathrm{GtC}]$$

And remember that this is the annual rate of emission.

Let’s quickly review what went into this calculation. We started with the annual global energy consumption at the present, which we can think of as being the product of the global population times the per capita energy consumption. Then we calculated the amount of CO₂ emitted per MJ of energy, based on different fractions of coal, oil, gas, and non-fossil energy sources — this is the emissions rate. Multiplying the emissions rate times the total energy consumed then gives us the global emissions of either CO₂ or just C.

We now see what is required to create an emissions scenario:

1. A projection of global population
2. A projection of the per capita energy demand
3. A projection of the fractions of our energy provided by different sources
4. Emissions rates for the various energy sources

In this list, the first three are variables — the 4^th is just a matter of chemistry. So, the first three constitute the three principal controls on carbon emissions.

Here is a diagram of a simple model that will allow us to set up emissions scenarios for the future:

Figure 8. Stella model of the emissions' calculation part of the model. This looks more complex than it really is due to the addition of 10 converters that enable the user to change the fraction of energy coming from different sources. The key result from this model is Total Emissions, in Gt C per year, which then controls the flow of carbon into the atmosphere of the global carbon cycle part of the model (see Figure 9).

Click for a text description of Figure 8.

The image is a complex systems diagram titled "System Dynamics Model of Energy Consumption and Emissions," which illustrates the relationships and feedback loops between various factors related to energy consumption, population, and emissions. Here's a detailed breakdown:

Components:

1. Population: Represented by a rectangular box labeled "Population," which has arrows indicating influence from and to other components.
2. Pop Limit: A cloud-shaped symbol labeled "Pop Limit" with an arrow pointing to the "Population" box, indicating a limit or constraint on population growth.
3. net change: An arrow labeled "net change" connects from "Population" to a circular node, indicating the net change in population affecting other variables.
4. r: A circular node labeled "r" connected to "Population," representing the growth rate of the population.
5. per capita energy: Connected to "Population" with an arrow, indicating per capita energy consumption.
6. global energy consumption: A circular node connected to "per capita energy," representing the total global energy consumption.
7. Total Emissions: A rectangular box connected to "global energy consumption," representing the total emissions resulting from energy consumption.
8. RC: A central circular node labeled "RC," which seems to be a key regulatory or control factor influencing various energy sources.

Energy Sources and Emissions:

• f_gas: Connected to "RC," representing emissions from gas.
• f_oil: Connected to "RC," representing emissions from oil.
• f_coal: Connected to "RC," representing emissions from coal.
• er_gas: Connected to "f_gas," representing the energy ratio or efficiency for gas.
• er_oil: Connected to "f_oil," representing the energy ratio or efficiency for oil.
• er_coal: Connected to "f_coal," representing the energy ratio or efficiency for coal.
• er_renew: Connected to "RC," representing the energy ratio or efficiency for renewable energy.
• f_renew: Connected to "er_renew," representing emissions from renewable energy sources.

Switches and Reductions:

• Gas Switch: A diamond-shaped decision node connected to "f_gas," "f_change 3," and "gas red time," indicating a decision point for switching to or from gas.
• Oil Switch: Similar to Gas Switch, connected to "f_oil," "f_change 2," and "oil red time," for oil.
• Coal Switch: Connected to "f_coal," "f_change 1," and "coal red time," for coal.
• gas red time: Connected to "Gas Switch," indicating the time frame for gas reduction.
• f_gas reduction: An arrow from "Gas Switch" indicating the reduction in gas emissions.
• oil red time: Connected to "Oil Switch," indicating the time frame for oil reduction.
• f_oil reduction: An arrow from "Oil Switch" indicating the reduction in oil emissions.
• coal red time: Connected to "Coal Switch," indicating the time frame for coal reduction.
• f_coal reduction: An arrow from "Coal Switch" indicating the reduction in coal emissions.

Feeddack Loops:

• f_change 1, f_change 2, f_change 3: These nodes are connected to the respective switches (Coal, Oil, Gas) and "star," indicating changes or feedback loops affecting the energy mix over time.
• star: A central node labeled "star" with a value of 0.1, connected to "f_change 1," "f_change 2," and "f_change 3," possibly representing a rate of change or a multiplier effect in the system.

Connections:

• Arrows with labels like "er_gas," "er_oil," "er_coal," "er_renew" indicate the flow of influence from energy efficiency ratios to emissions.
• The diagram shows a network of interconnections where changes in one part of the system can influence others, particularly through the "RC" node, which seems to be a regulatory center affecting all energy sources and their emissions.

This diagram visualizes how population growth, energy consumption per capita, and the choice of energy sources (gas, oil, coal, renewable) interact to influence total emissions, with various feedback loops and decision points affecting the dynamics over time.

Credit: David Bice @ Penn State is licensed under CC-BY-NC-4.0

In this model, the per capita energy (a graph that you can change) is multiplied by the Population to give the global energy consumption, which is then multiplied by RC (the composite emissions rate) to give Total Emissions. Just as we saw in the sample calculation above, RC is a function of the fractions and emissions rates for the various sources. Note that the non-fossil fuel energy sources (nuclear, solar, wind, hydro, geothermal, etc.) are all lumped into a category called renew, because they are mostly renewable. The model includes a set of additional converters (circles) that allow you to change the proportional contributions from the different energy sources during the model run.

This emissions model is actually part of a much larger model that includes a global carbon cycle model and a climate model. Here is how it works — the Total Emissions transfers carbon from a reservoir called Fossil Fuels that represents all the Gigatons of carbon stored in oil, gas, and coal (they add up to 5000 Gt) into the atmosphere. Some of the carbon stays in the atmosphere, but the majority of it goes into plants, soil, and the oceans, cycling around between the reservoirs indicated below. The amount of carbon that stays in the atmosphere then determines the greenhouse forcing that affects the global temperature — you’ve already seen the climate model part of this. The carbon cycle part of the model is complicated, but it is a good one in the sense that if we plug in the known historical record of carbon emissions, it gives us the known historical CO₂ concentrations of the atmosphere. Here is a highly schematic version of the model:

Figure 9. Highly simplified sketch of the global carbon cycle part of the model. The global carbon cycle is essentially a set of interconnected reservoirs. Humans are affecting this cycle (red arrows), preventing it from finding a steady state. The fossil fuel burning flow (on right side above) is controlled by the part of the model that calculates the emissions.

Click for a text description of Figure 9.

The image is a flowchart diagram illustrating the global carbon cycle, showing the movement and storage of carbon in various parts of the Earth's system. Units are provided in gigatons of carbon (GT), where one gigaton equals one billion metric tons or 101510^{15}1015 grams. The diagram uses different colors to represent various carbon reservoirs and arrows to indicate the flow of carbon between these reservoirs. Red arrows indicate flows that are sensitive to human activities, while green arrows represent flows that are sensitive to temperature.

Carbon Reservoirs:

• Atmosphere: Contains 750 GT of carbon. It is connected to other parts of the cycle via various processes.
• Land Biota: Contains 610 GT of carbon, involved in processes like photosynthesis and respiration.
• Soil: Contains 1580 GT of carbon, connected to land biota through litter fall.
• Surface Oceans: Contains 970 GT of carbon, involved in ocean-atmosphere diffusion and upwelling & downwelling.
• Deep Oceans: Contains 38,000 GT of carbon, connected to surface oceans through upwelling & downwelling.
• Ocean Biota: Contains 3 GT of carbon, connected to surface oceans.
• Sedimentary Rocks: Contains 1,000,000 GT of carbon, connected to the deep oceans through sedimentation.
• Fossil Fuels: Contains 5000 GT of carbon, influencing the atmosphere through fossil fuel burning.
• Mantle: Connected to sedimentary rocks through subduction.

Carbon Flows (in GT/year):

• Atmosphere to Land Biota:
  • Photosynthesis: 110 GT/year (green arrow, temperature sensitive)
  • Burning: 50 GT/year (red arrow, human activity sensitive)
• Land Biota to Atmosphere:
  • Respiration: 59.4 GT/year (green arrow, temperature sensitive)
  • Burning/Farming: 50 GT/year (red arrow, human activity sensitive)
• Land Biota to Soil: Litter fall: 60 GT/year
• Soil to Atmosphere: Respiration: 60 GT/year (green arrow, temperature sensitive)
• Atmosphere to Surface Oceans: Ocean-atmosphere diffusion: 90 GT/year (green arrow, temperature sensitive)
• Surface Oceans to Atmosphere: Ocean-atmosphere diffusion: 90 GT/year (green arrow, temperature sensitive)
• Surface Oceans to Deep Oceans: Upwelling & downwelling: 105.6 GT/year
• Deep Oceans to Surface Oceans: Upwelling & downwelling: 96.2 GT/year
• Surface Oceans to Ocean Biota: 105 GT/year
• Ocean Biota to Surface Oceans: 105 GT/year
• Deep Oceans to Sedimentary Rocks: Sedimentation: 0.6 GT/year
• Sedimentary Rocks to Mantle: Subduction: 0.6 GT/year
• Fossil Fuels to Atmosphere: Fossil Fuel Burning: 9 GT/year (red arrow, human activity sensitive)
• Volcanic Eruptions: 0.6 GT/year from the mantle to the atmosphere (green arrow, temperature sensitive)

Notes:

• Numbers next to the arrows represent approximate annual flows in gigatons per year (GT/year).
• The diagram highlights the interaction between natural processes and human-induced changes in the carbon cycle, emphasizing the impact of activities like burning fossil fuels and land use changes (farming, burning).

Credit: David Bice @ Penn State is licensed under CC-BY-NC-4.0

Experiments with the Model

Important Instructions

1. In this exercise, we will work with a model of a system that has many parts — carbon cycle, climate model, population model, and energy model. We'll explore how making changes to one part of this system alter the behavior of other parts of the system. This illustrates an important part of what we call Systems Thinking, which is that in complex, connected systems, a change in one part may have consequences that spread throughout the system.
2. After watching the movie above, run the model [26]without making any changes to establish what we will call the “control” case for these experiments. You can return to this control case by hitting the Restore All Devices button.
3. Write down the Total Emissions at the year 2100 — this will be our comparison point in time for later experiments.Look at page 2 of the graph pad, which shows human emissions, which is essentially the same as Total Emissions except that it is limited by the total amount of fossil fuel carbon we have; if we burn through all that carbon, human emissions will drop to 0, and in fact, you’ll see that it drops off to zero about the year 2165 — this is when we run out of fossil fuels. So if we haven’t solved our energy problems by then, we’re in deep trouble!

The table above gives you a set of instructions related to the practice and graded versions of the summative assessment, including which switch to turn on, the fractional reduction, and the time over which this reduction takes place. As one of the fossil fuel sources is reduced, the model increases the renewable fraction so that the total of all the fractions stays at 1.0.

1. How much does switching from one of the fossil fuel sources to renewables decrease the emissions in the year 2100? First, run the model as is when you open it (all switches are in the off position) and take note of the total emissions for the year 2100 on graph #1 (this is our control case), then make the changes prescribed in the table above and find the new emissions in the year 2100 and then calculate the difference from the control case.

Difference = (±2 Gt)

Practice Answer = 11.3

2. Does this change lead to a leveling off of emissions, or do they continue to climb?

1. Levels off
2. Continues to climb [correct answer for practice version]

3. Which has a bigger impact in reducing emissions — limiting population growth to 10 billion, or reducing your fossil fuel fractions as prescribed? Here, make sure all the switches are turned off, and then set the Pop Limit to 10.

1. Population limitation
2. Fossil fuel reduction [correct answer for practice version]

Reset the Pop Limit to 12 when you are done with this one.

4. How much does reducing all of the fossil fuel sources to a fraction of 0.05 decrease the emissions in the year 2100 compared to the control case (set all switches to the off position for the control)? Set the start time to 2020, then turn on all the switches, and set the f reductions so that each fossil fuel source ends up at 0.05 after 30 years. You can check to make sure you’ve done this correctly by looking at the fractions on page 4 of the graph pad.

Set all of the reduction times to 20 years. For the graded version, lower the fossil fuel sources to a fraction of 0.1; leave everything else the same as the practice version.

Difference = (±2 Gt)

Practice Answer = 23.8

Follow these steps:

1. Run the control case (don’t make any changes to the model)
2. Turn on all the switches
3. Set all the reduction times to 20
4. Set f coal reduction to 0.22; f oil reduction to 0.28; f gas reduction to 0.16
5. Run the model again — you should now see a blue curve from the control run and a pink curve from the modified run (looking at graph #1)
6. Run the cursor along the control case curve until you get to the year 2100 and write down the total emissions at that point — it should be 29.57 (the units are Gt C/yr).
7. Run the cursor along the modified case curve (pink one) until you get to the year 2100 and write down the total emissions at that point — it should be 5.74.
8. The question is asking for the difference in emissions, so subtract 5.74 from 29.57 and you get 23.83 Gt C/yr — this is the reduction in emissions we would achieve if we lowered all of the fossil fuels to just 5% of our total energy consumption.

5. Which has the bigger impact in reducing emissions — halting the rise in per capita energy use, or reducing our fossil fuel fractions? For this one, you’ll use your answer to the above question (#4) and compare to one in which you turn off all the switches, and then change the per capita energy graph so that it is more or less a straight line all the way across. You can check to see how well you’ve done this by looking at page 8 of the graph pad after you run the model. So, which has a bigger impact in reducing emissions?

This table refers to the question below — it provides a set of model settings that lead to stabilization of emissions.

Refer to the worksheet to see what your per capita energy graphs should look like for the practice and graded versions.

6. One of the main goals people mention in the context of future global warming is halting the growth of our emissions of CO₂. As you have seen so far, there are a variety of ways to reduce that growth. Now, let’s see what happens when we stabilize emissions. Modify the original model to create the emissions scenario defined by the parameters supplied in the table above — this should result in an emissions history that more or less stabilizes. Then find the emissions in the year 2100.

Total Emissions in 2100 = ±2.0 Gt C/yr

Practice version — 11.3 Gt C/yr

7. Now that you have an emissions scenario that stabilizes (the human emissions of carbon remain more or less constant over most of the time), let’s look at temperature (page 9 of the graph pad). Remember that global temperature change in this model is the warming relative to the pre-industrial world, which is already about 1°C in 2010, the starting time for our model. What is the global temperature change in the year 2100?

Global temperature change = ±0.5 °C

Practice version — 2.6°C

8. Now study the temperature change (graph#9) and the pCO2 atm (the atmospheric concentration of CO₂ in ppm or parts per million — page 10 of the graph pad) for the time period following the stabilization of emissions. Does the stabilization of emissions lead to a stabilization of temperature or atmospheric CO₂ concentration?

1. Fossil fuel reduction [correct answer for practice version]
2. Per capita energy change (i.e., conservation + efficiency)

Reset the model before going to the next question.

9. Now, let’s say we want to keep the warming to less than 2°C, which the IPCC recently decided was a good target — warming more than that will result in damages that would be difficult to manage (we would survive, but it might not be pretty). We have seen by now that it is simply not enough to stabilize emissions at a level similar to or greater than today’s — that leads to continued warming. So we need to reduce emissions relative to our present level, which will be hard with a growing population and economy (and thus a growing per capita energy demand).

So, let’s see what is necessary to stay under that 2° limit, given some constraints. In all cases, we’ll assume that we can get our oil and gas fractions down to 0.1 (i.e., 10% each) over a time period of 30 years with a start time of 2020. We’ll leave population out of it (keep the limit at 12 billion), and for the practice version, we’ll make the assumption that per capita energy demand remains constant at a level of 75 for the whole time period (modify the graph so that it is a horizontal line at a level of 75 on the y-axis). This leaves f coal reduction as our main variable. The time period for reducing coal will be 30 years. You can change four scenarios for coal reduction as follows:

A: Keep the coal fraction unchanged (switch off)

B: Reduce the coal fraction to 10% (so f coal reduction would be .17)

C: Reduce the coal fraction to 5% (set f coal reduction to .22)

D: Reduce the coal fraction to 0% (set f coal reduction to .27)

For the graded version, we will change the per capita energy demand graph so that it drops to 50 by the year 2086 (see worksheet for a picture of what the graph should look like).

Find the coal fraction that keeps the temperature closest to 2°C by the year 2200.

Coal reduction scenario (A,B,C, or D):

Practice version: D is the correct answer

We’re done with this model for now, but you will be coming back to something similar to this later on when you do your capstone projects. You’ll use the model to design an emissions and energy consumption scenario for the future for which you’ll also explore the environmental and economic consequences.

The following questions encourage you to step back and think about what you’ve learned here. Short answers will suffice here.

10. What are the three principal variables that determine how much carbon is emitted from our production of energy? (Hint: look at page 11 of this worksheet)

11. What is the relationship between economic development (growth) and per capita energy consumption? (Hint: look at figure 7 of this worksheet)

12. Among the various sources of our energy, which has the highest rate of CO₂ emitted per unit of energy? (Hint: look at table on page 10 of this worksheet)

13. What happens to the atmospheric concentration of CO₂, and thus the global temperature, if we stabilize (hold constant) the emissions rate? (refer to question #8 above)

14. Can we stay under the 2°C warming limit in the year 2200 by completely eliminating our reliance on fossil fuel energy sources alone (reducing coal, oil, and gas to 0% of our energy supply), or do we also need to reduce our energy consumption per capita? (make appropriate changes and then run the model to figure this out)

1. both stabilize
2. neither stabilizes — both increase [correct answer for practice]
3. neither stabilizes — both decrease
4. CO2 goes up; temperature goes down
5. CO2 goes down; temperature goes up