Lesson 5: Hypothesis testing and randomization
Overview
Overview
This lesson covers "hypothesis testing", a set of methods that provide a rational framework for evaluating how different a sample is from a specific value or how different two samples are from each other. While confidence intervals address the question "How much could my sample statistic vary?", hypothesis testing answers the question "Given the potential variation in my sample statistic, is the statistic I measured significantly different than X ?", where X is some specific value. This lesson will teach you hypothesis testing using "randomization distributions", which is a methodology very similar to the bootstrapping you learned for confidence intervals. The data manipulation and visualization coding tools you've learned in previous lessons will be important here for preparing datasets for hypothesis testing and presenting the results.
This lesson starts with a general overview of hypothesis testing and how to form hypotheses, followed by an introduction to randomization distributions. Data from the 2021 Texas Power Crisis provide an example of how to prepare your data for a number of different hypothesis tests. As the lesson goes through these different kinds of hypothesis tests, pay attention to the similarities in the Python code for constructing the randomization distributions; this same structure can be adopted to test many other different statistics not covered in this lesson.
Learning Outcomes
By the end of this lesson, you should be able to:
- write statistical hypotheses;
- perform a hypothesis test using randomization;
- interpret a p-value;
- construct a hypothesis test for single proportion;
- compare two samples with hypothesis testing;
- explain significance level and Type I error;
- experiment with sample size to see impact on p-value;
- identify when data have paired observations;
- devise a randomization strategy for paired data
Lesson Roadmap
| Type | Assignment | Location |
|---|---|---|
| To Read | Lock, et. al. 4.1-4.5 | Textbook |
| To Do |
Complete Homework:
Take Quiz |
Canvas Canvas |
Questions?
If you prefer to use email:
If you have any questions, please send a message through Canvas. We will check daily to respond. If your question is one that is relevant to the entire class, we may respond to the entire class rather than individually.
If you prefer to use the discussion forums:
If you have questions, please feel free to post them to the General Questions and Discussion forum in Canvas. While you are there, feel free to post your own responses if you, too, are able to help a classmate.
Introduction to Hypothesis Testing
Introduction to Hypothesis Testing
In many instances, it is not clear whether a data sample supports a claim about the population from which it came. Some examples include:
- One might want to see if particulate matter (PM2.5) pollution exceeds healthy concentration levels in economically disadvantaged areas. The population is the air in all economically disadvantaged areas over a long period of time. It is infeasible to collect data for the whole population, so one collects air quality samples from several areas at several different times throughout the year. Hypothesis testing then answers the question: do the sampled data indicate that the average PM2.5 concentration is statistically significantly greater than the limit to be deemed healthy?
- A popular electric car company has heard reports that some of the individual cars it has made do not meet the mileage range, on a single charge, reported by the company. If the proportion of such defective cars is greater than a certain amount, the company needs to recall that particular vehicle model and pay to repair all the cars. The population is all the individual cars of that model. Since it is impossible to test the entire population to see if the range is met or not, the company randomly samples 100 of the cars and tests them. Hypothesis testing then answers the question: is the proportion of defective cars less than the limit for issuing a recall?
- A natural gas company has come up with a new well design that they think will boost production. Here there are two populations: the population of wells with the new design and the population of wells with the old design. The population parameter of interest is the difference in natural gas production between the two populations. Since it is financially risky to drill a whole bunch of wells with the new design (enough to constitute a population), they drill a few new wells with this design. The company then samples the amount of production from the new wells and compares the average to the average production from the old wells. Hypothesis testing then answers the question: is average production from the new wells statistically significantly greater than the average production from the old wells?
In order to perform hypothesis testing, one needs a unbiased sample from a population that has variability in the measure of interest. If, for example, the PM2.5 concentration was constant across all areas and all times, then one single measurement would equal the population average, and one could make a definitive statement about this population average without hypothesis testing. There would be no uncertainty in this population parameter. Using a biased sample in a hypothesis test may lead to a false conclusion. If, for example, the electric car company only tested the next 100 cars produced from only one of its factories, it may miss that the defect is originating from another factory.
As we go through this lesson, you will see that all hypothesis testing follows a similar process:
- Formulate your null and alternative hypotheses
- Calculate the relevant sample statistic
- Conduct the hypothesis test: compute the randomization distribution
- (Optional) Visualize the randomization distribution and sample statistic
- Calculate the p-value
- State the conclusion of your hypothesis test
Even before these steps, an incredibly useful, if not necessary, preliminary step is to explore your data. Visualizations and five-number summaries will help you formulate appropriate hypotheses, which is important for interpreting the results of the subsequent steps.
Throughout this lesson, the hypothesis testing will be conducted via randomization distributions. Besides allowing you to practice your Python coding, this simulation-based approach provides a more intuitive understanding of what a p-value means and how it is determined, as compared to the method traditionally presented in a statistics class. Furthermore, this randomization distribution approach is flexible and widely-adaptable to other statistics besides the means and proportions we'll cover in this lesson.
This lesson will start by going over the guidelines for formulating your hypotheses, and then will go into the concept of randomization distributions. Data from the Texas Power Crisis of 2021 will be used to exemplify several different common varieties of hypothesis tests, and the lesson will conclude with some important considerations to sample size, significance, and multiple testing.
Formulating and Writing Hypotheses
Formulating and Writing Hypotheses
After exploring and visualizing your data, the first step to hypothesis testing is writing your hypotheses to test. Data visualization and summarizing your data (e.g., with the ) help in formulating these hypotheses, in particular with defining the appropriate inequality (whether to use < or > or ≠) in the alternative hypothesis. We can break down the formulation of hypotheses into the following steps below.
Three Steps to Writing a Hypothesis
-
Write your question in plain language. Based upon the data at hand, and the prior exploratory data analysis (e.g., visualization, summarizing), what question are you seeking to answer? An example might be: “Are PM2.5 concentrations unsafe in certain areas?” It is important to frame the question such that it can answered by the data you have. For instance, you wouldn’t want to ask a question about all pollution when you only have data on particulate matter concentration.
-
Write your hypothesis in plain language. The goal in this step is to take a stance on the answer to the question posed in Step 1. Following the example given above, a viable hypothesis is: “Yes, PM2.5 concentrations are at unsafe levels.” This statement doesn’t need to be correct, since the rest of the hypothesis testing procedure will test this statement. In particular, it will tell you whether or not the data support this statement.
-
Write your statistical hypotheses. The task here is really to convert your plain-language hypothesis from Step 2 into statistical notation. Specifically, it needs to be written in terms of the appropriate population parameter for your question. For example, in order to say that PM2.5 concentrations are safe or unsafe, we can look at the mean (), since this would capture the general, average PM2.5 conditions. Furthermore, it needs to be written in terms of two different hypotheses:
-
The null hypothesis (or just “null” for short). Here you are stating that the population parameter for your variable of interest is equal to a specific value (single-sample tests) or another population parameter (two-sample tests). Again, this is a hypothesis so it does not need to be correct; this is what will be tested. The null hypothesis should capture the contradiction to your hypothesis from Step 2. So, for example, with the EPA defining the threshold between safe and unsafe PM2.5 levels as 12 micrograms per cubic meter (40 C.F.R. § 50.18 (2013) [1]), our null hypothesis would be . (You might be wondering why ≤ is not used instead of =, since safe levels would be anything at or below . Indeed, many statistics texts introduce the null hypothesis this way, and really either way is allowable. However, when using ≤ (or ≥ in other situations), you end up only testing the = portion of this statement anyway.)
-
The alternative hypothesis (“alternative” for short). Here you are replacing the equality in the null hypothesis with an inequality (>, <, or ≠). The correct choice is that which aligns with your hypothesis in Step 2. So, following the example above, our alternative hypothesis is , because any average PM2.5 exceeding is unsafe.
-
The subsequent hypothesis testing procedure will give us a quantitative metric (the p-value) for saying whether or not the data support the alternative hypothesis. This is framed as either:
-
We reject the null hypothesis in favor of the alternative hypothesis, or
-
We fail to reject the null hypothesis.
Note that the focus here is on rejecting or not rejecting the null hypothesis. This is because the null contains the equality statement, and thus something definitive to test. However, as we will see later, this null is tested against the alternative, which is why in the first option we can say “in favor of the alternative”.
Parameters
Because our statistical hypotheses need to written in terms of the population parameters, let's review some common parameters in the table below:
| Population Parameter | Sample Statistic | |
|---|---|---|
| Mean | ||
| Proportion | ||
| Standard Deviation | ||
| Correlation | ||
| Slope (linear regression) | ||
| Difference of Means | ||
| Difference of Proportions |
This lesson will only cover tests for some of these parameters, and correlation and slope will be covered in Linear Regression.
 Assess It: Check Your Knowledge
Assess It: Check Your Knowledge
Knowledge Check
Hypothesis Testing: Randomization Distributions
Hypothesis Testing: Randomization Distributions
Like bootstrap distributions, randomization distributions tell us about the spread of possible sample statistics. However, while bootstrap distributions originate from the raw sample data, randomization distributions simulate what sort of sample statistics values we should see if the null hypothesis is true. This is key to using randomization distributions for hypothesis testing, where we can then compare our actual sample statistic (from the raw data) to the range of what we'd expect if the null hypothesis were to be true (i.e., the randomization distribution).
Randomization Procedure
The procedure for generating a randomization distribution, and subsequently comparing to the actual sample statistic for hypothesis testing, is depicted in the figure below.
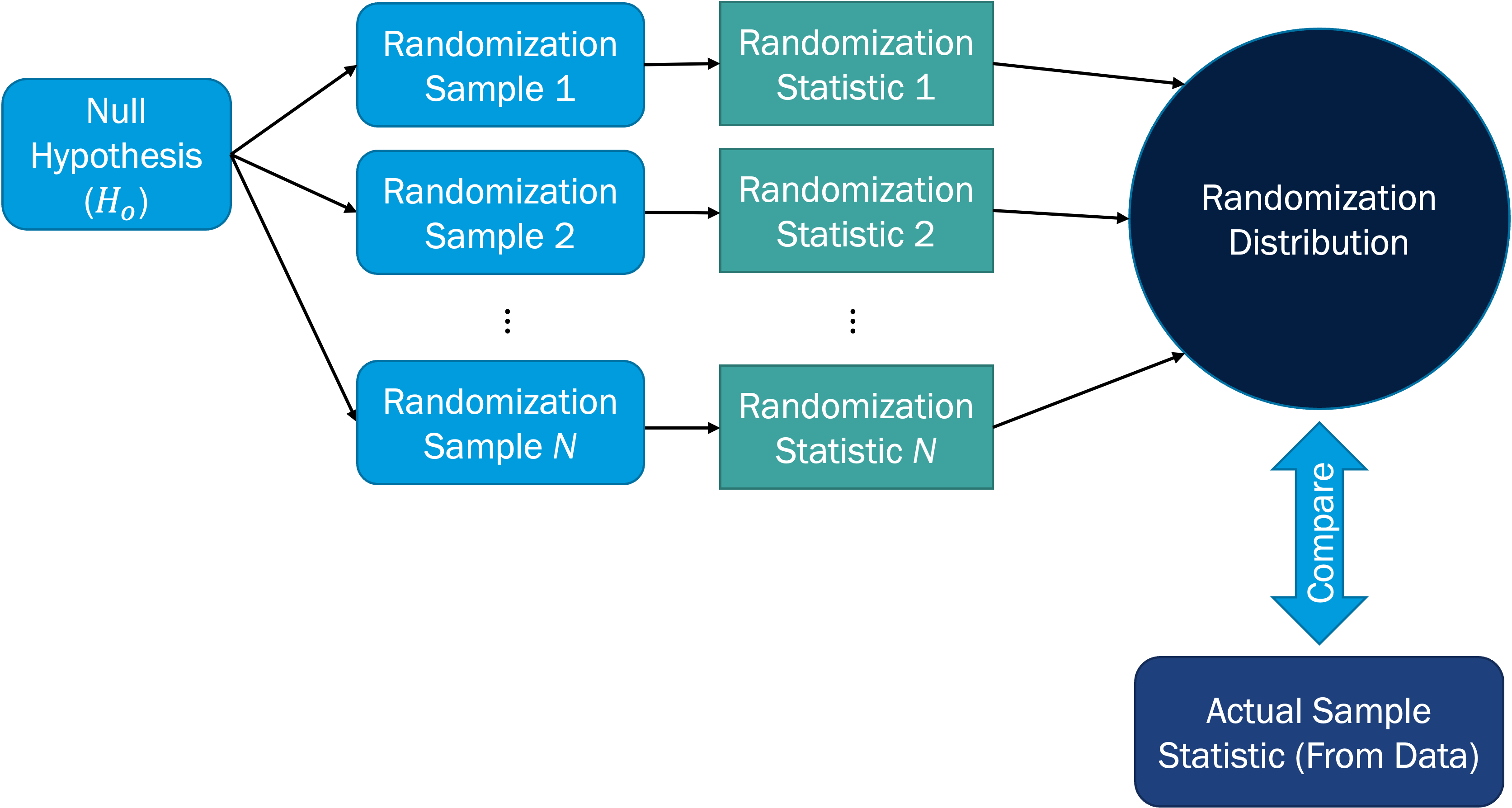
The pseudo-code (general coding steps, not written in a specific coding language) for generating a randomization distribution is:
-
Obtain a sample of size n
-
For i in 1, 2, ..., N
-
Manipulate and randomize sample so that the null hypothesis condition is met. It is important that this new sample has the same size as the original sample (n).
-
Calculate the statistic of interest for the ith randomized sample
-
Store this value as the ith randomized statistic
-
-
Combine all N randomized statistics into the randomization distribution
Here, we've set the number of randomization samples to N = 1000, which is safe to use and which you can use as the default for this course. The validity of the randomization distribution depends on having a large enough number of samples, so it is not recommended to go below N = 1000. In the end, we have a vector or array of sample statistic values; that is our randomization distribution.
As we'll see in the subsequent pages, we'll use different strategies for simulating conditions under the assumption of the null hypothesis being true (Step 2.1 above). The choice of strategy will depend on the type of testing we're doing (e.g., single mean vs. single proportion vs. ...). Generally speaking, the goal of each strategy is to have the collection of sample statistics agree with the null hypothesis value on average, while maintaining the level of variability contained in the original sample data. This is really important, because our goal with hypothesis testing is to see what could occur just by random chance alone, given the null conditions are true, and then compare our data (representing what is actually happening in reality) to that range of possibilities.
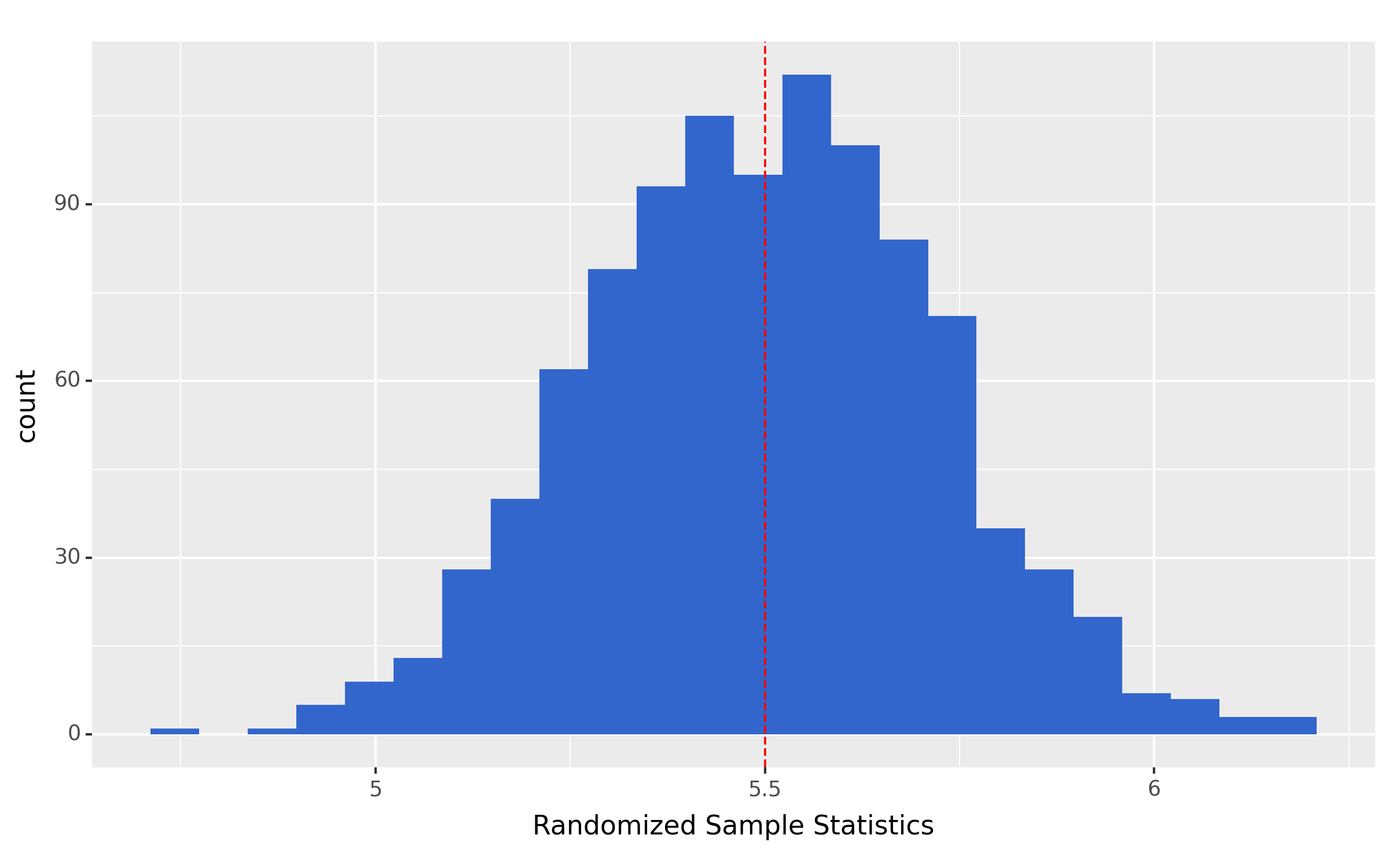
- The randomization distribution is centered on the value in the null hypothesis (the null value).
- The spread of the randomization distribution describes what sample statistic values would occur with random chance and given the null hypothesis is true.
The figure below exemplifies these key features, where the histogram represents the randomization distribution and the vertical red dashed line is on the null value.
The p-value
Our goal with the randomization distribution is to see how likely our actual sample statistic is to occur, given that the null hypothesis is true. This measure of likelihood is quantified by the p-value:
Let's elaborate on some important aspects of this definition and provide guidance on how to determine the p-value:
- The p-value is a probability, so it has a value between 0 and 1.
- This probability is measured as the proportion of samples in the randomization distribution that are at least as extreme as the observed sample (from the original data)
- "at least as extreme" refers to the inequality in the alternative hypothesis, and so:
- If the alternative is < (a.k.a. "left-tailed test"), the p-value = the proportion of samples the sample statistic.
- If the alternative is > (a.k.a. "right-tailed test"), the p-value = the proportion of samples the sample statistic.
- If the alternative is (a.k.a. "two-tailed test"), the p-value = twice the smaller of: the proportion of samples the sample statistic or the proportion of samples the sample statistic
The default threshold for rejecting or not rejecting the null hypothesis is 0.05, refer to as the "significance level" (more on this later). Thus,
- If the p-value < 0.05, we can reject the null hypothesis (in favor of the alternative hypothesis)
- If the p-value > 0.05, we fail to reject the null hypothesis
Although it should be noted that some researchers are moving away from the classical paradigm and starting to think of the p-value on more of a continuous scale, where smaller values are more indicative of rejecting the null.
 Assess It: Check Your Knowledge
Assess It: Check Your Knowledge
Motivating Example: 2021 Texas Power Crisis
Motivating Example: 2021 Texas Power Crisis
Before we progress into some of the common types of hypothesis tests, let's introduce the data and problem that will be used to exemplify these tests. As an example of hypothesis testing, we'll examine wind and natural gas power generation during the Texas Power Crisis of Feb. 14-15, 2021. An excellent article about the event is in Gold, R. (2022) The Texas Electric Grid Failure Was a Warm-up. Texas Monthly, Feb. 2022 [3]. Data are from ERCOT and available in L11_IntGenbyFuel2021.csv [4], accessed from ERCOT on Sep. 19, 2021. This contains power generation from all fuel types for all of Feb. 2021, reported in 15-minute intervals.
In addition to these power generation data, ERCOT forecasted the peak capacity from wind as 6.1 GW and from natural gas as 48.4 GW. These are their predictions of how much each energy source would need to generate in order to meet demand during the unusually cold winter storms associated with this event.
Some important terminology that is used in this example includes:
-
Capacity - the maximum amount of power that a generator can produce at a particular time
-
Forecasted peak capacity - the anticipated amount of power needed to meet peak demand
-
Generation - the power produced from a source (generator)
Also, bear in mind that for units of power we'll use:
1,000,000,000 W (watts) = 1,000,000 kW (kilowatts) = 1,000 MW (megawatts) = 1 GW (gigawatt)
and for energy:
 Watch It: Video - 2021 Texas Power Crisis (29:05 minutes)
Watch It: Video - 2021 Texas Power Crisis (29:05 minutes)
The Google Colab Notebook use in the above video is available here [5], and the data are here [6]. For the Colab file, remember to click "File" then "Save a copy in Drive". For the data, it is recommended to save to your Google Drive.
The general question we will ask with this dataset is:
We will answer this question in different ways, using different forms of hypothesis testing, in the subsequent pages.
Hypothesis Test for Single Mean
Hypothesis Test for Single Mean
If you have a single sample, and are concerned with showing that its mean is significantly larger or smaller than some value (which will be the null value), then you want to perform a "single mean test".
 Read It: Hypothesis Test for Single Mean
Read It: Hypothesis Test for Single Mean
In a single mean test, your statistical hypotheses will take the following form, and your statistic, computed on both the original sample and the randomized samples, is :
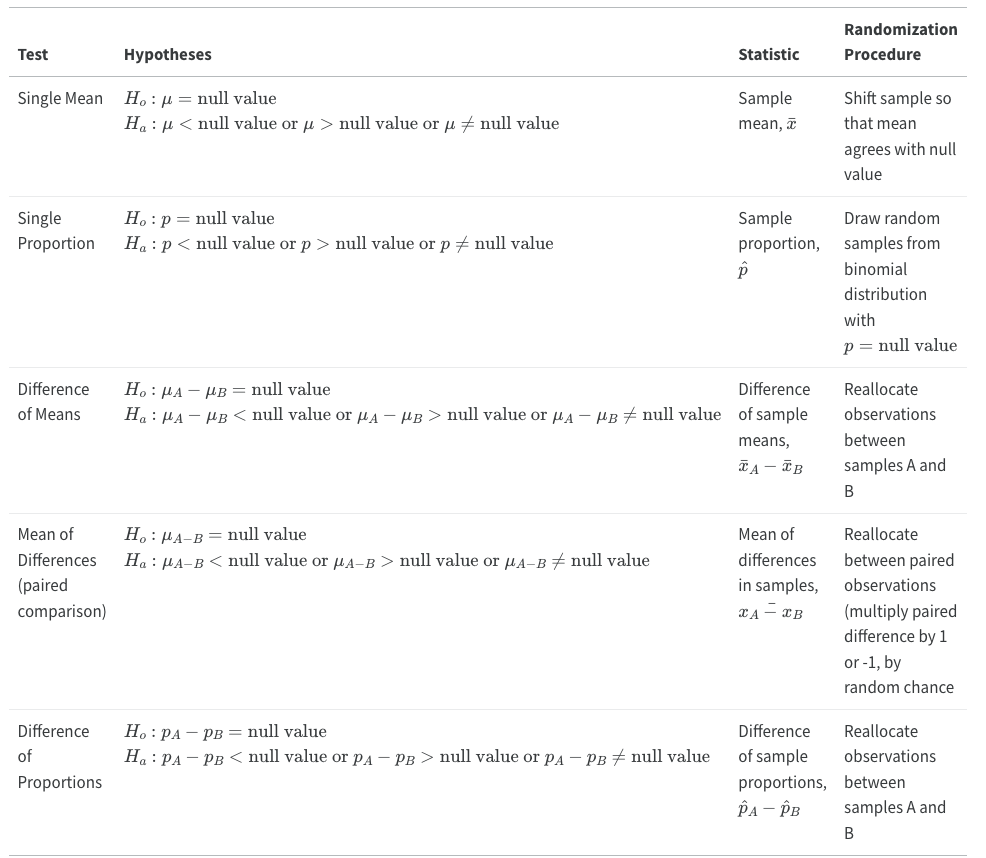
| Test | Hypotheses | Statistic | Randomization Procedure |
|---|---|---|---|
| Single Mean | or |
Sample mean, | Shift sample so that mean agrees with null value |
The null value will typically be some threshold or standard that you are comparing your sample mean against. Going back to the PM2.5 example earlier in this lesson, the null value for that single mean test is 12.5 micrograms per cubic meter.
Randomization Procedure
The randomization procedure that we will use for a test of a single mean involves shifting all the values in the original sample by a uniform amount, such that the resulting sample mean equals the null value, . The amount to shift all values by is the difference between and the original sample mean, . The pseudo-code for this procedure is:
-
Obtain a sample of size n
-
Calculate:
-
For i in 1, 2, ..., N
-
Randomly draw a new sample, of size n, with replacement from the shifted sample, .
-
Calculate the sample mean for this new randomized sample
-
Store this value as the ith randomized statistic
-
-
Combine all N randomized statistics into the randomization distribution
Random drawing of values with replacement allows for the possibility of values being drawn more than once, and with equal probability each time.
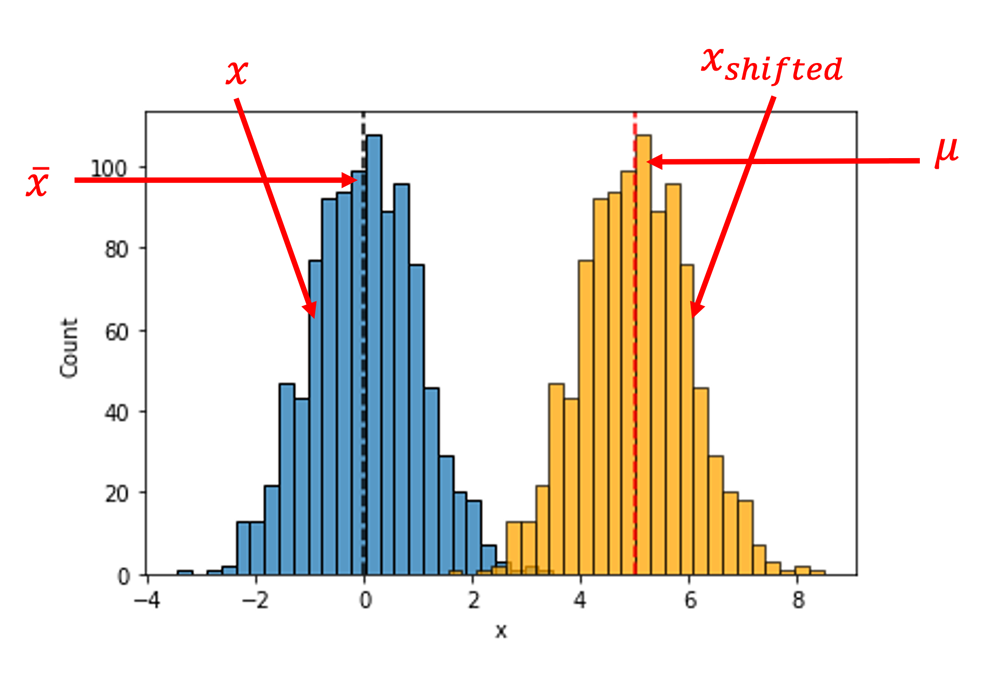
The figure below provides an example of this randomization procedure. The blue histogram represents the original sample data, centered at , and the yellow histogram depicts the shifted sample which is now centered at the null value, . Note that the two histograms share the exact same shape, and thus the same spread.
The following video demonstrates how to implement this procedure in Python, using the 2021 Texas Power Crisis as an example.
 Watch It: Video - Hypothesis Test for Single Mean (15:34 minutes)
Watch It: Video - Hypothesis Test for Single Mean (15:34 minutes)
The Google Colab Notebook use in the above video is available here [5], and the data are here [6]. For the Colab file, remember to click "File" then "Save a copy in Drive". For the data, it is recommended to save to your Google Drive.
 Try It: Tesla Range Scandal
Try It: Tesla Range Scandal
A class-action lawsuit [7], filed August 2nd, 2023, essentially alleges that Tesla, the electric vehicle company, grossly exaggerated the ranges on some of its vehicles. Plaintiffs claim that the rated ranges on their Tesla cars are much larger than actual ranges they get under normal driving conditions. The lawsuit includes several Tesla models, one of which being the Model S. Plug In America collects self-reported survey data on EV performance, including the Model S [8]. In this example, we'll look at the 70 kWh, dual motor ("70D") version of the Model S, with a rated range of 240 miles. We will exclude any cars with more than 10,000 miles on the odometer. As of this writing, the dataset includes a sample of 5 of these cars.
Our question here is "Do the actual ranges of the Model S 70D fall significantly below the rated range of 240 miles?" Our hypothesis could be: "Yes, they do fall below." Thus, our statistical hypotheses are:
Develop Python code below to test these hypotheses, and calculate a p-value. The knowledge check will then ask about the conclusion of this test.
 Assess It: Check Your Knowledge
Assess It: Check Your Knowledge
Knowledge Check
Hypothesis Test for Single Proportion
Hypothesis Test for Single Proportion
A test for a single proportion is for when you have one sample and are interested in a proportion from it.
 Read It: Hypothesis Test for Single Proportion
Read It: Hypothesis Test for Single Proportion
In a single proportion test, your statistical hypotheses will take the following form, and your statistic, computed on both the original sample and the randomized samples, is :
| Test | Hypotheses | Statistic | Randomization Procedure |
|---|---|---|---|
| Single Proportion | or or |
Sample proportion, | Draw random samples from binomial distribution with |
As with the test for a single mean, the null value will typically be some threshold or standard that you are comparing your sample proportion against. For proportions, a common null value is 0.5, since this denotes fair odds between two options (e.g., a coin flip). Often, one wants to see whether or not something is diverging from this pure random chance behavior.
Randomization Procedure
The randomization procedure that we will use for a test of a single proportion involves simulating random samples from a binomial distribution, such that the values in each random sample are drawn according to the null value, . The binomial distribution only applies to a binary system, where there are only two categories in a categorical variable. Take, for example, a series of coin flips where we are interest in the proportion of heads:
We can simulate a series of coin flips (or similar process) using the binomial distribution. In Python, we can use:
x = np.random.binomial(n, p, N)
where n is the sample size (e.g., number of flips), p is the null value (e.g., 0.5 because the default is that the coin is fair), and N is the number samples (e.g., 1000 or some similarly large positive integer). The output, x, is a vector of length N that contains the numerator of the proportion of interest for each sample (e.g., the number of heads in each series of coin flips).
The pseudo-code for this procedure is:
-
Obtain a sample of size n
-
Simulate N numerators of the proportion of interest from the binomial distribution, each with sample size n and probability p = null value.
-
Calculate the sample proportions for these new randomized sample numerators by dividing each by the sample size, n.
-
Combine all N randomized statistics into the randomization distribution
Note that this procedure does not explicity require a "for" loop, as Step 2 is performing the simulation from the binomial distribution for all intended samples, N.
The following video demonstrates how to implement this procedure in Python, using the 2021 Texas Power Crisis as an example.
 Watch It: Video - Hypothesis Test for Single Proportion (10:46 minutes)
Watch It: Video - Hypothesis Test for Single Proportion (10:46 minutes)
The Google Colab Notebook use in the above video is available here [5], and the data are here [6]. For the Colab file, remember to click "File" then "Save a copy in Drive". For the data, it is recommended to save to your Google Drive.
 Try It: Is the rate of acute lymphoblastic leukemia (ALL) in PA significantly different than the national rate?
Try It: Is the rate of acute lymphoblastic leukemia (ALL) in PA significantly different than the national rate?
In a recent study (Clark et al., 2022 [9]), researchers at Yale University find that proximity to hydraulic fracturing (a.k.a. "fracking") sites almost doubles the odds of a child getting acute lymphoblastic leukemia (ALL). Their study examines 405 Pennsylvania children with this form of leukemia between 2009-2017, when oil and gas development activity (including fracking) was at a high in PA. For a comparison, they also examine a "control group" of 2,080 randomly-selected children of similar age as those with leukemia (randomly-selected from a pool of 2,019,054 children, by Dr. Morgan's count).
The following two-way table is taken from Table 2 in the paper:
| Fracking Exposure | Children w/ ALL | Children w/o ALL |
|---|---|---|
| Exposed | 6 | 16 |
| Unexposed | 399 | 2064 |
This table shows the number of children who had ALL that had oil and gas development activity within 2km uphill from their residence ("Exposed"; 6 children) and those who were "Unexposed" to oil and gas development activity (didn't have oil and gas operations within 2km uphill from them). The third column shows the same counts for children without ALL.
In order to answer the question in the section title and look at the rate of ALL, you need to know that the total number of children in PA, corresponding to the years of the study above, is 2,019,054 (PA Department of Health, Birth Statistics [10]). You also need to know that the national rate during the time period of the study is about 32 cases per 1 million, or 0.000032 (Ward et al., 2014 [11]). Let's define "rate" as:
In the DataCamp code window below, design and conduct a test for single proportion:
- Write your null and alternative hypotheses.
- Perform the hypothesis test using a randomization distribution.
- Report the p-value.
- What is the conclusion of your test? State this in terms of the hypotheses, and also in terms of the original question above. Make sure to indicate the significance level you are using.
 Assess It: Check Your Knowledge
Assess It: Check Your Knowledge
Knowledge Check
Two Sample Comparison: Wind vs. Natural Gas
Two Sample Comparison: Wind vs. Natural Gas
 Read It: Two Sample Comparison
Read It: Two Sample Comparison
The next few hypothesis tests we'll introduce are for when one wants to compare one sample to another, and in particular infer a relationship between their respective population parameters.
Continuing with motivating example from the 2021 Texas Power Crisis, we will now look at comparing samples of wind versus natural gas power generation. The following video shows the additional data processing steps in Python for enabling this two sample comparison. In particular, since these two sources have very different levels of power generation, we need to calculate a different variable in order to compare these samples fairly. This variable is the "percent deficit", which captures the percent of the forecasted peak capacity that each source has met.
 Watch It: Video - Two Sample Comparison: Wind vs. Natural Gas (6:00 minutes)
Watch It: Video - Two Sample Comparison: Wind vs. Natural Gas (6:00 minutes)
Hypothesis Test for Difference of Means
Hypothesis Test for Difference of Means
If you want to compare the mean of one population to the mean of another population, and you have samples from each population, then you want to perform a difference of means test.
 Read It: Hypothesis Test for Difference of Means
Read It: Hypothesis Test for Difference of Means
In a difference of means test, your statistical hypotheses will take the following form, and your statistic, computed on both the original sample and the randomized samples, is , where A and B just refer to two separate samples, belonging to two separate populations:
| Test | Hypotheses | Statistic | Randomization Procedure |
|---|---|---|---|
| Difference of Means | or or |
Difference of sample means, | Reallocate observations between samples A and B |
Typically, the nuill value here is 0, since the null hypothesis is usually that the two population means are equal, and thus their difference is zero.
Randomization Procedure
The randomization procedure that we will use for a difference of means test is called "reallocation". Reallocation involves randomly swapping values between the two samples, where each value has the same probability of moving to the other sample or staying in its original sample. The reasoning behind this strategy is that, if the null hypothesis is true and there is no difference between the two populations, then it shouldn't matter from which population the sample data originate. If we have our sample data organized into a DataFrame similar to the table depicted in the figure below, then reallocation can efficiently be accomplished by randomly drawing values (in the "Value" column) without replacement. In other words, simply re-ordering the values in that column.
The pseudo-code for this procedure is:
-
Obtain two samples of size n and m, respectively.
-
Organize the values of both samples into a DataFrame, with the sample ID in one column and their respective values in another.
-
For i in 1, 2, ... N
-
Randomly sample the value column without replacement.
-
Calculate the sample means for each sample (e.g., by grouping by the sample ID).
-
Find the difference of the sample means. Make sure to do this in the same order as stated in the hypotheses!
-
-
Combine all N randomized statistics into the randomization distribution
Note that the two sample sizes, n and m, do not need to be equal. However, you may run into problems if one sample is very small and one is large.
The following video demonstrates how to implement this procedure in Python, using the 2021 Texas Power Crisis as an example.
 Watch It: Video - Hypothesis Test for Difference of Means (12:21 minutes)
Watch It: Video - Hypothesis Test for Difference of Means (12:21 minutes)
The Google Colab Notebook use in the above video is available here [5], and the data are here [6]. For the Colab file, remember to click "File" then "Save a copy in Drive". For the data, it is recommended to save to your Google Drive.
 Try It: Comparing Tesla Ranges Across Different Mileages
Try It: Comparing Tesla Ranges Across Different Mileages
The following example somewhat continues from the example in Hypothesis Test for a Single Mean, but it doesn't depend on that example or its results. Plug In America collects self-reported survey data on EV performance, including the Model S [8]. In this example, we'll look at the 70 kWh, dual motor ("70D") version of the Model S, with a rated range of 240 miles. Let's further break these cars down into two categories: "Low" mileage when the odometer read less than or equal to 10,000 miles, and "High" mileage when the odometer is greater than 10,000 miles. 10,000 miles is an arbitrary threshold here, and feel free to repeat this analysis with your own definition of low versus high mileage.
Our question here is "Do the actual ranges of the Model S 70D differ from low to high mileage?" Our hypothesis could be: "Yes, the range decreases at high mileage." Thus, our statistical hypotheses are:
Develop Python code below to test these hypotheses and calculate a p-value. The knowledge check will then ask about the conclusion of this test.
 Assess It: Check Your Knowledge
Assess It: Check Your Knowledge
Knowledge Check
Hypothesis Test for Mean of Differences (Paired Comparison)
Hypothesis Test for Mean of Differences (Paired Comparison)
 Read It: Hypothesis Test for Mean of Differences (Paired Comparison)
Read It: Hypothesis Test for Mean of Differences (Paired Comparison)
In the situation where you want to compare the mean of one population to the mean of another population, and you have samples from each population whose values you can pair on some rational basis, then it is better to do a paired comparison than to perform the difference of means test in the previous page. The key here is that you have a good reason to pair the values from one sample to the other sample. For example:
- You want to see whether temperature affects the range (miles it can drive on a single charge) of Tesla Model S cars. So you take 5 cars and measure their range on a summer day, and then again on winter day, with the same 5 cars. Your two samples are then "warm range" and "cold range". It is then advisable to pair warm range and cold range for each individual car.
In a mean of differences test, your statistical hypotheses will take the following form, and your statistic, computed on both the original sample and the randomized samples, is , the mean of the paired differences between sample A and sample B:
| Test | Hypotheses | Statistic | Randomization Procedure |
|---|---|---|---|
| Mean of Differences (paired comparison) |
or or |
Mean of differences in samples, | Reallocate between paired observations (multiply paired difference by 1 or -1, by random chance) |
As before, the nuill value here is 0, since the null hypothesis is usually that the two population means are equal, and thus their difference is zero.
Randomization Procedure
As with the difference of means randomization procedure, we will also use reallocation for the mean of differences. However, instead of reallocating across the entire samples, we will restrict our reallocation to the pairs of value. In other words, we will enforce the pairing the observations across the two samples, and each pair of values has the same change of randomly swapping between samples. Thus, the reasoning that we had for reallocation before still holds true: if the null hypothesis is true and there is no difference between the two populations, then it shouldn't matter from which population the sample data originate.
The figure below illustrates how we can organize our DataFrame to maintain pairing across samples. Here, we have a variable generically called "pairing" to denote that it serves as the basis for pairing values across Sample A and Sample B.
It turns out, that instead of physically reallocating paired values across Sample A and Sample B and then taking their differences again, it is computationally easier to simply find the difference of the pairs once, and then randomly multiply these difference by 1 or -1 (which effectively re-orders the terms in the difference equation). The pseudo-code for this procedure is:
-
Obtain two samples, each of size n, with paired observations.
-
Find the differences of the paired observations.
-
For i in 1, 2, ... N
-
Randomly multiply each difference by 1 or -1.
-
Calculate the mean of the adjusted differences.
-
-
Combine all N randomized statistics into the randomization distribution
The following video demonstrates how to implement this procedure in Python, using the 2021 Texas Power Crisis as an example.
 Watch It: Video - Hypothesis Test for Mean of Differences (10:37 minutes)
Watch It: Video - Hypothesis Test for Mean of Differences (10:37 minutes)
The Google Colab Notebook use in the above video is available here [5], and the data are here [6]. For the Colab file, remember to click "File" then "Save a copy in Drive". For the data, it is recommended to save to your Google Drive.
 Assess It: Check Your Knowledge
Assess It: Check Your Knowledge
Knowledge Check
Hypothesis Test for Difference of Proportions
Hypothesis Test for Difference of Proportions
If you want to compare the proportion of one population to the proportion of another population, and you have samples from each population, then you want to perform a difference of proportions test.
 Read It: Hypothesis Test for Difference of Proportions
Read It: Hypothesis Test for Difference of Proportions
In a difference of proportions test, your statistical hypotheses will take the following form, and your statistic, computed on both the original sample and the randomized samples, is , where A and B just refer to two separate samples, belonging to two separate populations:
| Test | Hypotheses | Statistic | Randomization Procedure |
|---|---|---|---|
| Difference of Proportions | or or |
Difference of sample proportions, | Reallocate observations between samples A and B |
Typically, the nuill value here is 0, since the null hypothesis is usually that the two population proportions are equal, and thus their difference is zero.
Randomization Procedure
The randomization procedure for a difference of proportions test follows the same reallocation strategy as with the difference of means. Specifically, the pseudo-code for this procedure is:
-
Obtain two samples of size n and m, respectively.
-
Organize the values of both samples into a DataFrame, with the sample ID in one column and their respective values in another.
-
For i in 1, 2, ... N
-
Randomly sample the value column without replacement.
-
Calculate the sample proportions for each sample (e.g., by grouping by the sample ID).
-
Find the difference of the sample proportions. Make sure to do this in the same order as stated in the hypotheses!
-
-
Combine all N randomized statistics into the randomization distribution
Again, the two sample sizes, n and m, do not need to be equal, but you may run into problems if one sample is very small and one is large.
The following video demonstrates how to implement this procedure in Python, using the 2021 Texas Power Crisis as an example.
 Watch It: Video - Hypothesis Test for Difference of Proportions (11:41 minutes)
Watch It: Video - Hypothesis Test for Difference of Proportions (11:41 minutes)
The Google Colab Notebook use in the above video is available here [5], and the data are here [6]. For the Colab file, remember to click "File" then "Save a copy in Drive". For the data, it is recommended to save to your Google Drive.
 Try It: In PA, is the rate of acute lymphoblastic leukemia (ALL) among those exposed to fracking significantly different than the rate of ALL among those not exposed to fracking?
Try It: In PA, is the rate of acute lymphoblastic leukemia (ALL) among those exposed to fracking significantly different than the rate of ALL among those not exposed to fracking?
The following exercise builds off of the Try It exercise from "Hypothesis Test for Single Proportion [12]". Recall from that page that:
In a recent study (Clark et al., 2022 [9]), researchers at Yale University find that proximity to hydraulic fracturing (a.k.a. "fracking") sites almost doubles the odds of a child getting acute lymphoblastic leukemia (ALL). Their study examines 405 Pennsylvania children with this form of leukemia between 2009-2017, when oil and gas development activity (including fracking) was at a high in PA. For a comparison, they also examine a "control group" of 2,080 randomly-selected children of similar age as those with leukemia (randomly-selected from a pool of 2,019,054 children, by Dr. Morgan's count).
The following two-way table is taken from Table 2 in the paper:
| Fracking Exposure | Children w/ ALL | Children w/o ALL |
|---|---|---|
| Exposed | 6 | 16 |
| Unexposed | 399 | 2064 |
This table shows the number of children who had ALL that had oil and gas development activity within 2km uphill from their residence ("Exposed"; 6 children) and those who were "Unexposed" to oil and gas development activity (didn't have oil and gas operations within 2km uphill from them). The third column shows the same counts for children without ALL.
Again, let's define "rate" as:
and we can further call for the exposed group , and for the unexposed group .
In the DataCamp code window below, design and conduct a test ro compare these proportions:
- Write your null and alternative hypotheses.
- Perform the hypothesis test using a randomization distribution.
- Report the p-value.
- What is the conclusion of your test? State this in terms of the hypotheses, and also in terms of the original question above. Make sure to indicate the significance level you are using.
Effect of Sample Size
Effect of Sample Size
 Read It: The Effect of Sample Size in Hypothesis Testing
Read It: The Effect of Sample Size in Hypothesis Testing
-
A larger sample size will lead to a narrower randomization distribution. Usually, this will lower the p-value. In other words, if you have a large sample, you can more definitively reject the null hypothesis when the sample statistic is close to the null value.
-
A smaller sample size will lead to a wider randomization distribution. Usually, this will increase the p-value. In other words, if you have a small sample, it is less likely you can reject the null hypothesis when the sample statistic is close to the null value.
MORE DATA IS ALWAYS BETTER!!!
The following video presents a numerical experiment where we can see the effect of sample size on the randomization distribution and the p-value.
 Watch It: Video Effect of Sample Size - (12:06 minutes)
Watch It: Video Effect of Sample Size - (12:06 minutes)
The Google Colab Notebook use in the above video is available here [5], and the data are here [6]. For the Colab file, remember to click "File" then "Save a copy in Drive". For the data, it is recommended to save to your Google Drive.
 Try It: Coin Flips
Try It: Coin Flips
Imagine you have a coin that you suspect is "unfair", meaning that it is weighted more to one side. You decide to test the coin with a series of flips, where the number of flips is your sample size, n. In this series of flips, you record the proportion of "heads", and it comes out to 0.6 (regardless of the magnitude of n). With your hypotheses being:
- Ho: p = 0.5
- Ha: p > 0.5
write code in the DataCamp cell below to report the p-value and the standard error of the randomization distribution under two conditions: 1) when n = 10 flips, and 2) when n = 100 flips. What happens to the standard error as your sample size increases? What happens to the p-value?
Significance Level & Multiple Testing
Significance Level & Multiple Testing
 Read It: Significance Level
Read It: Significance Level
Why do we use 0.05 as the threshold for deciding if a p-value is low enough to reject the null hypothesis? Well... we don't have to!
"0.05" is the default value of the significance level, noted with α. Other typical values it can take are 0.10 and 0.01. Any p-value that falls below your chosen significance level will indicate statistically-significant evidence against the null hypothesis.
A smaller significance level will require stronger evidence to reject the null hypothesis.
In other words, with all else being equal, the sample statistic will have to be further away from the center of the randomization distribution to reject the null.
 Read It: Multiple Testing
Read It: Multiple Testing
The significance level also represents the probability of committing "Type I" error with a hypothesis test. This refers to falsely rejecting the null hypothesis, when in actuality the null hypothesis is true. For example, take our default of α = 0.05. A randomization distribution shows what sample statistics to expect with the null hypothesis being true. So, data could arise, under the condition of the null being true, that would yield a sample statistic that falls in the lower-most or upper-most 5% of the randomization distribution. The probability of this happening is 0.05, or the significance level in this example.
 Try It: A Numerical Experiment for Multiple Testing
Try It: A Numerical Experiment for Multiple Testing
The DataCamp below has code for running multiple experiments. Each experiment tests whether we have a normal deck of playing cards, insofar as it contains 26 red cards and 26 black cards (in other words, 50% of each color). The population here is the normal deck of playing cards, and each experiment randomly draws a sample of n = 9 cards from the deck, with replacement (so, putting each card back into the deck after it is drawn). Let's say that our proportion of interest, p, stands for the proportion of red cards. Thus, our hypotheses are:
- Ho: p = 0.5
- Ha: p ≠ 0.5
For each experiment, we then test the hypothesis using a randomization distribution, find the p-value for that test, and record it in the object "p-vals". Run the code a few times. In each run, what proportion of p-values are less than the default significance level of 0.05? For those p-values, the conclusion is to reject the null hypothesis; in other words, the experimental data support the deck NOT being normal. Of course, we have the luxury of knowing in this situation that the deck is, in fact, normal. Thus, these low p-values represent cases of Type I error, where the null hypothesis is falsely rejected.
Edit the code to adjust the significance level from 0.05 to 0.01. How many cases of Type I error do you have now?
Note on the Code: "if" Statements
The code above contains an example of an "if" statement in order to find the smallest tail for calculating the p-value of the two-tailed test. The general structure of an "if" statement follows:
1 2 3 4 5 6 7 | if LOGICAL CONDITION: CODE TO RUN IF LOGICAL CONDITION IS METelse: CODE TO RUN IF LOGICAL CONDITION IS NOT MET |
One could have multiple lines of code in the CODE TO RUN spaces. This can be extended to include other logical conditions:
1 2 3 4 5 6 7 8 9 10 11 | if FIRST LOGICAL CONDITION: CODE TO RUN IF FIRST LOGICAL CONDITION IS METelif SECOND LOGICAL CONDITION: CODE TO RUN IF SECOND LOGICAL CONDITION IS METelse: CODE TO RUN IF NEITHER LOGICAL CONDITION IS NOT MET |
Furthermore, the "else" statement at the end is optional; you could choose to run no code if the logical condition(s) is/are not met.
Summary
Summary
By now, you may have observed a theme in developing randomization distributions for hypothesis testing. Without giving specific code, our hypothesis testing procedure generally goes like this:
- Formulate null and alternative hypotheses
- Calculate the sample statistic from original data
- Compute the randomization distribution
- Simulate new sample under the condition of the null hypothesis being true
- Calculate the sample statistic from new, simulated sample
- Repeat many times and save the collection of simulated sample statistics (this collection is your randomization distribution)
- [Optional, but recommended] Visualize the randomization distribution and original sample statistic (histograms or dotplots are great for this)
- Find the p-value as the proportion of simulated sample statistics that are at least as extreme as the original sample statistic
- State the conclusion of your hypothesis test, in the context of the original hypotheses and larger problem
The table below summarizes the various tests that we've covered so far, but bear in mind that as long as you can calculate a statistic (a single-valued summary) from your data and formulate hypotheses, you can adopt the framework above to perform a hypothesis test. This is a valuable feature of the randomization approach!
| Test | Hypotheses | Statistic | Randomization Procedure |
|---|---|---|---|
| Single Mean | or or |
Sample mean, | Shift sample so that mean agrees with null value |
| Single Proportion | or or |
Sample proportion, | Draw random samples from binomial distribution with |
| Difference of Means | or or |
Difference of sample means, | Reallocate observations between samples A and B |
| Mean of Differences (paired comparison) |
or or |
Mean of differences in samples, | Reallocate between paired observations (multiply paired difference by 1 or -1, by random chance |
| Difference of Proportions | or or |
Difference of sample proportions, | Reallocate observations between samples A and B |
A major challenge is figuring out which form of hypothesis test is appropriate for your given problem. The flowchart below can help, and reviewing problems in this course and textbook will help you build a sense of what test to perform.
 Assess It: Check Your Knowledge Quiz
Assess It: Check Your Knowledge Quiz
Reminder - Complete all of the Lesson 5 tasks!
You have reached the end of Lesson 5! Double-check the to-do list on the Lesson 5 Overview page to make sure you have completed all of the activities listed there before you begin Lesson 6.