Lesson 8: Linear regression

Overview

Recall from Lesson 3 that you learned how to create scatter plots with a best fit line. When you created this plot, you were visualizing the result of linear regression! In this lesson, we will delve deeper into linear regression, as well as return to the concept of correlation that we introduced earlier in the course. We will discuss the traditional way of conducting linear regression in addition to several built-in functions in Python. You will learn how to implement linear regression, run hypothesis tests for various parts of the linear regression analysis, and interpret results from the different analyses.

Learning Outcomes

By the end of this lesson, you should be able to:

assess whether two variables are associated based on their correlation coefficient
explain the simple linear model; solve for the slope and intercept of a regression line in Python
test a calculated slope value for significance
interpret R-squared values
contrast confidence intervals vs. prediction intervals for linear regression; produce both in Python

Lesson Roadmap

Table listing assignments
Type	Assignment	Location
To Read	Lock et. al. 9.1-9.3	Textbook
To Do	Complete Homework: H10 Linear Regression Take Quiz 8	Canvas

Questions?

If you prefer to use email:

If you have any questions, please send a message through Canvas. We will check daily to respond. If your question is one that is relevant to the entire class, we may respond to the entire class rather than individually.

If you prefer to use the discussion forums:

If you have questions, please feel free to post them to the General Questions and Discussion forum in Canvas. While you are there, feel free to post your own responses if you, too, are able to help a classmate.

Review of Correlation

Read It: Review of Correlation

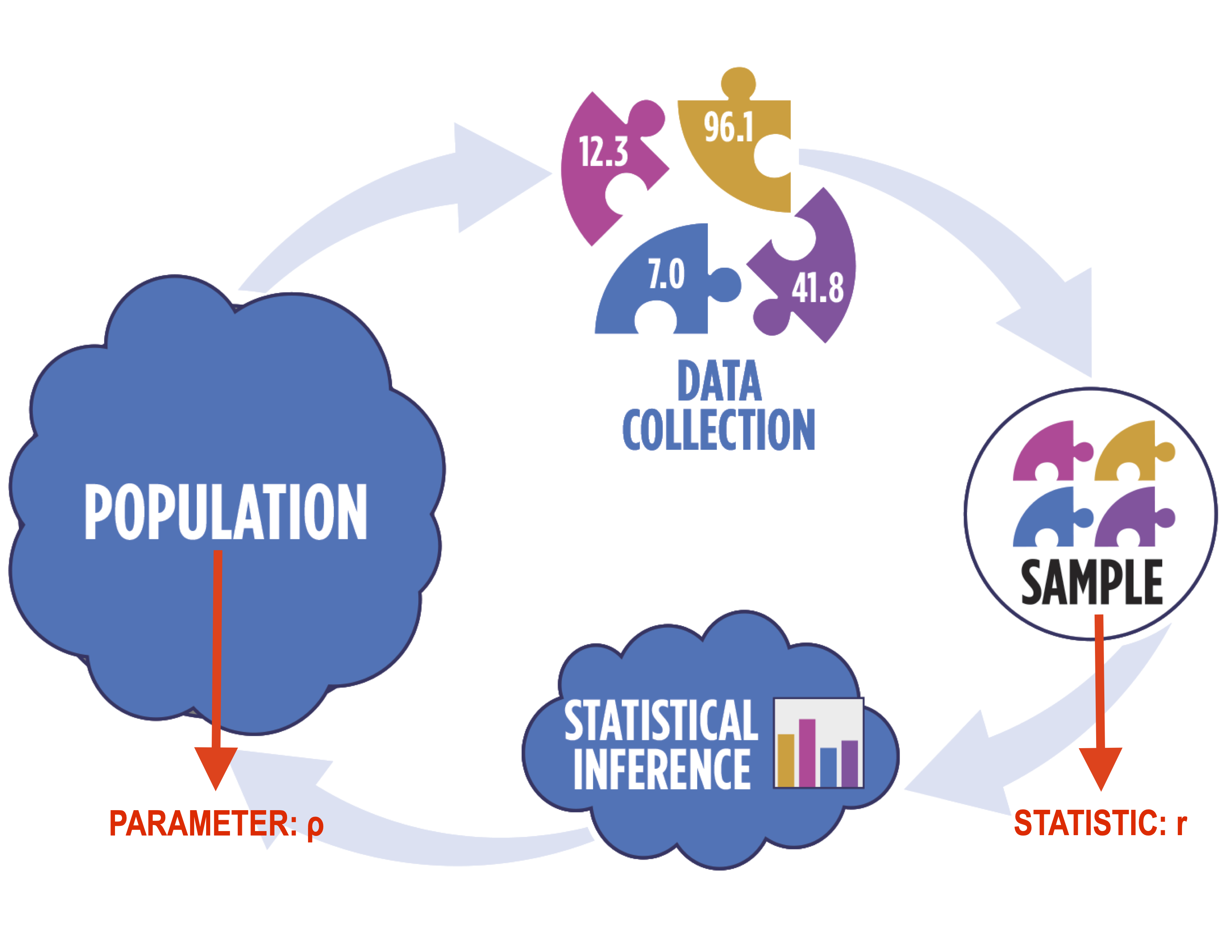
Recall from Lesson 3 when we discussed correlation as a means of describing relationships. In that lesson, we primarily focused on qualitative assessment of the correlation. In particular, when working with correlation, you need to use distinct notation, as shown below. In particular, we use the Greek letter “rho” (ρ) to denote the population correlation and the Latin letter “r” to denote the sample correlation.

Recall the population and sample illustration from before. Here, we show the notation for correlation, with “rho” representing the population correlation and “r” representing the sample correlation.

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [1]

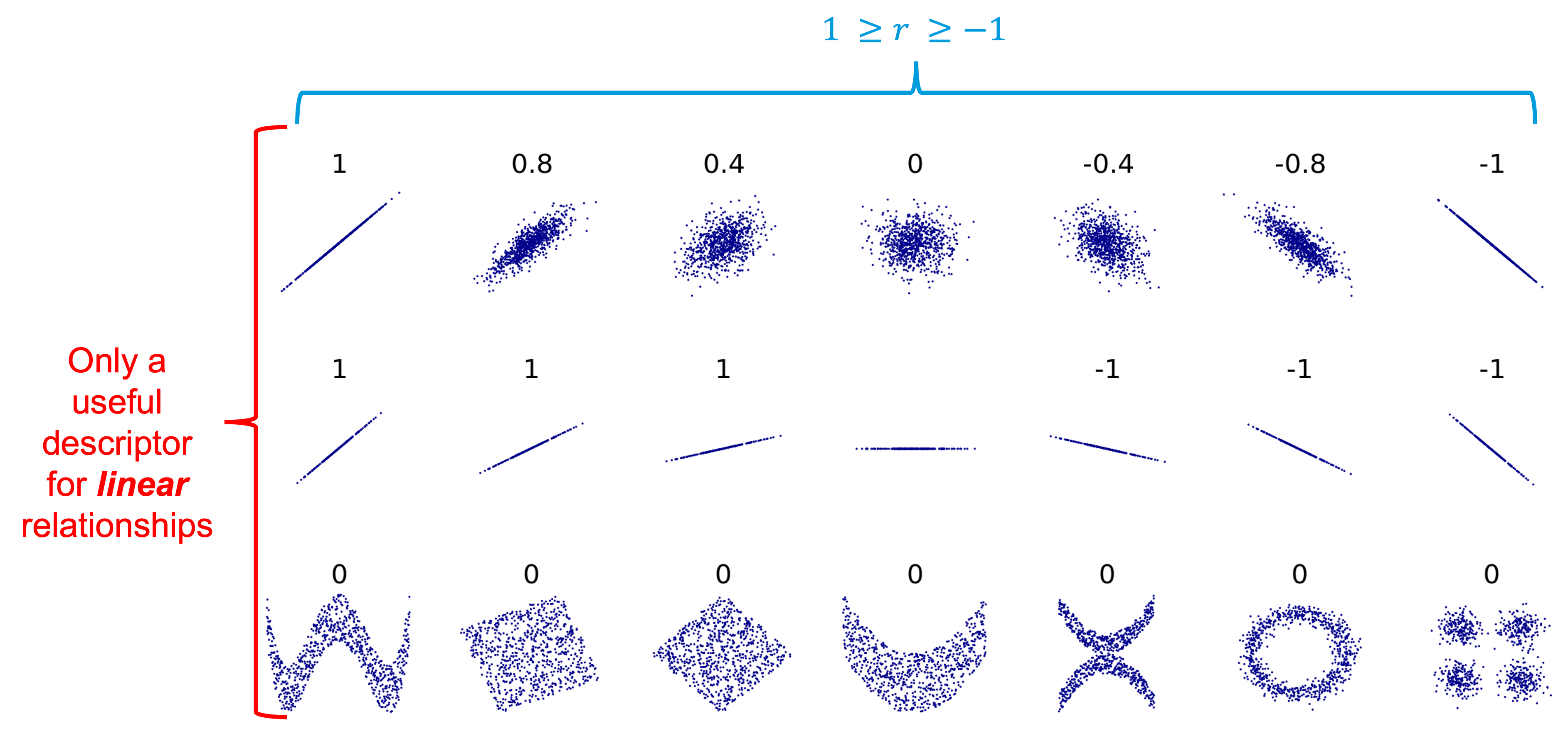
In terms of correlation, the values typically range from -1 to 1, with values at the edge of the range representing strong correlation (positive or negative, depending on the sign) while values closer to 0 represent weak correlation. The figure below shows possible correlation values. It is important to note, however, that correlation is only applicable to linear relationships! Non-linear relationships can have associations, but they will always have a correlation of 0, as shown below.

Enter image and alt text here. No sizes!

Demonstration of different values for correlation coefficients.

Credit: This file is made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication [2].

Below is a video where we demonstrate some key coding principles related to finding the correlation between two variables.

Watch It: Video - Introduction Correlation (11:37 minutes)

Click here for a transcript.

Hello, and welcome to a new lesson on linear regression. So throughout this lesson we're going to walk you through a series of tests and ways in which we can conduct linear regression. In particular, this video is going to focus on correlation and how we can actually conduct eventually a hypothesis test for testing the significance of correlation. So we're going to start with an introduction to the subject, and then later we'll get into the actual hypothesis test.

So, we are here in Google Colab, and we have several libraries that we're going to use that we've all used before in different settings. And in particular, we're going to ask the question, does... we're going to test the significance of correlation, so we're going to ask the question, “Does using more water for fracking yield more natural gas production?” And so, if you're not familiar, there's some context here provided that you can read through on your own time. But essentially, we are going to be using data from the Marcellus Shale formation in Pennsylvania to test, to answer this question. So there's two CSV files that we're going to use. And I have them ready to go and read in. The first one is lecture eight, Marcellus Wells and the second one is lecture twenty, Pennsylvania Wells Frack. And so, both of these have data on fracking wells, but they have a little bit of a different, different columns. And so, we can see here for in the Marcellus data which I've called Marc, we've got all of this information about drilling. And what we're going to be interested in is the data down here, total gas and max gas. These are the values that tell us how much gas was produced from a well. The water data on the other hand, has less columns. So we've got basically what we're interested in is total base water volume. And there's a few other extra things. So before we can actually get into working with this data, we need to merge it together. So we need to do a little bit of pre-processing. And we also need to do some grouping. So the first thing we're going to do is group the water data. So I'm just going to call this water2 so that I don't override my original data frame. I'm going to say water dot group by, and I want to group my API number. So the API number is a way to identify the actual well that we are referring to. And this water data set has multiple values for multiple wells. And so, we need to essentially group them all together. And we want to get the total for that well over the entire study period.

So to give you a look about what this now looks like after I run that, I'm using that dot head command to print the first five rows. And essentially we've sort of condensed our data set down to API number and total base water volume, as opposed to having multiple columns up here. Because I'm not grouping them, I'm not storing them. So, they just sort of drop off, which is fine because we really only need the API number and the total base water volume. So, now we've grouped the data, the next step is to merge our water data in our wells data. However before we can do that, you look up here we've got this API number column but it has a different name than our API number column here. Now these are the same API numbers, they're just called different things for the different data sets. So, in order to merge on them we actually need to rename the column. And so, we don't need to rename every column, we just need to change API N o to API number, so that it matches what the water data set has. And then in that same block of code I'm going to go ahead and merge our data frame using td.merge and say marc water2. We're going to do an inner join so that we only keep data points that are in both columns. and we're going to join on our newly renamed API number and again I will print the first five rows. And so, here we can see we've got this big data set now. If we scroll to the end now we've got our total base water volume at the very end to go with our total gas column.

And so, this is the data set that we're going to use throughout the correlation lectures. But before we get started with correlation, a good habit to be in is to visualize our data so we know what is going on. So we're going to use ggplot with merge_df, and I'm going to do a little bit of a different modeling or visualization technique. And, I'm going to put our AES command within the larger ggplot command. So it's still going to look the same. I'm still going to have an X value and a Y value which is going to be total gas. But the benefit to doing it this way is that these AES statements carry throughout the whole plotting thing, so when I go to do geom_point I don't need to actually type anything. I don't need to provide an AES statement because it carries it down from the main ggplot command. And that makes this go a little easier because then we can add our stat_smooth. Again, we don't need to give it the AES. We do still need to specify a linear model and we can change the color to red.

And so, here we have what the total base water volume in the total gas looks like. And now we could make some qualitative statements about the correlation. Here we can say that it is positively correlated and that maybe if I had to estimate it might be about 0.4, maybe, just based off of the example thoughts that we have to go off of. But again, we haven't added any numerical quantity to that yet, and in order to do that we need to find the sample correlation coefficient, which is r. So, I'm actually going to do this inside a print statement. So, I'm going to say correlation coefficient, and then I'm going to do a round statement so that it's not printing a bunch of different, a bunch of extra numbers. We really only need a few. And then I'm going to give the command for finding the correlation of sample data. So we can say merge_df total base water volume and then the command after the square bracket is dot core open parentheses.

And then we just give the second variable, total gas. And then there's one more thing that we need to do, and that's to finish off our round command. And so it's going to be right here. So you can see how the parentheses are highlighted. So we're still inside that round command, but we're outside of the correlation command. And I'm going to say comma three, which rounds to three decimal places. So we can print it out. And say the correlation coefficient is 49, or 0.494, which is actually,

it's okay. It's not the best correlation coefficient that we have, but it's not terrible. And so, based off of this plot and this correlation coefficient, we can write a conclusion. So, generally when we're thinking about correlation, our core, our conclusion should focus on the direction of the associations of the relationship between the two variables and the evidence for this relationship. And so, I'm just going to paste in some text that I had preloaded and say that to make this conclusion, we can say there is a positive association between total water volume and total gas, which means as total water volume increases, the total gas increases. And the evidence for this is the correlation coefficient, which is positive, and the slope of the line which we can see is also positive. And so, this is sort of a basic way to make do some inference from correlation, but it's still a bit qualitative. It's not, although we do have a quantitative number, it's not necessarily the most statistically sound. And so, what we'll do in the next video is conduct a hypothesis test in order to get at more of that statistical inference instead of just looking solely at one sample.

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [1]

Try It: DataCamp - Apply Your Coding Skills

Using the partial code below, find the correlation coefficient between the variables x and y.

1
2
# libraries
import pandas as pd
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

1/0 0/0

Assess It: Check Your Knowledge

Knowledge Check

Randomization Procedure for Correlation

Read It: Randomization Procedure for Correlation

To conduct the randomization procedure for correlation, we will return to np.random.choice, which we used in Lesson 5 to conduct the hypothesis tests. The first step in the procedure is to define the hypotheses. For correlation tests, the hypotheses follow the same basic formula in which the null hypothesis assumes no correlation (i.e., ρ = 0) and the alternative hypothesis is some inequality of that (e.g., ρ > 0, ρ < 0, or ρ != 0), as indicated below.

$H_{o} : ρ = 0$

$H_{a} : ρ > 0, or ρ < 0, or ρ \neq 0$

Once the hypotheses are defined, we can begin the randomization procedure. The main difference between this procedure and previous iterations is that we only shuffle one of the variables we are interested in. For example, say we have the following data:

ID	x	y
A	1	4
B	2	5
C	3	6

In this case, we want to randomly sample either x or y without replacement (i.e., reallocate the data for only one variable). If we choose to randomly sample y, for example, the data may then look like this:

ID	x	y
A	1	6
B	2	4
C	3	5

Note that all of the original y data is still there, it is simply in a new order, since we sampled without replacement. This procedure effectively breaks the pairs, so we can see if the correlation value was significantly different than 0--if the correlation is close to 0, then it won't matter if we break the pairs, but if the correlation is far from 0, it is more likely to matter and lead to a lower correlation value. Once the random sampling is completed, we recalculate the correlation coefficient with the new pairs, store that value, and repeat for a sufficiently large number of iterations (e.g., N = 1000). Below is a video demonstrating this procedure.

Watch It: Video - Hypothesis Testing Correlation (10:25 minutes)

Click here for a transcript.

Welcome back to the videos on correlation. Today we're going to continue to talk about correlation, but we're going to get into that statistical inference side. And in particular, I'm going to introduce to you how to conduct a hypothesis test for testing the significance of correlation. So, let's jump in.

So, here we are in Google Colab. I've already loaded in the data. We're still working with that Marcellus Well Shale or Marcellus well and water data that we used up here to make this conclusion. But we're going to do a bit more of a quantitative analysis and focus on hypothesis testing today. And so, the first step in any hypothesis test is to state the hypotheses. And so, our null hypothesis is rho, the Greek letter, equals zero. And it's always going to be this correlation because of the significance test for correlation is whether or not the correlation is significantly different from zero. And so we have rho equals zero. And then our alternative here is that rho is greater than zero. Now this could be less than, this could be not equal to, but for this case I'm going to go greater than zero. And so once those are stated then we need to conduct the randomization procedure. And I've outlined these steps here, so that you can have them later when thinking about the randomization procedure. But we start with data. And now in the past we've shuffled data around. We've done reallocation randomization. In this case we're going to do a reallocation of sorts, but we're only going to do it with one variable. So say we start with this data here, X and Y. What we're then going to have to do is choose one variable to shuffle. Here I'm doing Y, and we sample without replacement, so reallocating the data for that one variable, and then we're going to recalculate the correlation coefficient and repeat that n number of times. And really the goal with this reallocation is to break the pairs. So we don't want to keep them paired together, we want to break them and then recalculate the correlation. Because if the correlation is equal to zero, then it shouldn't matter how much we shuffle the data, it should always be equal to zero. And so by shuffling we can sort of get at that significance level. And so we can go ahead and get started with the code. So the first thing we need to do is define our sample correlation coefficient. And I'll call it samp_core. And this is just how we calculated the correlation before, total basewatervolume dot core with total gas.

So this is our sample correlation. And then before we get into our randomization loop, we need to initialize the variables. So I'm going to make a copy because we don't want python to accidentally override our original data frame. So I'm going to call it sim. We need capital N for 1000 iterations. We need lowercase n, which is our sample size, which I'm just going to set to be the number of rows in our simulated, our copied data set. And then we need to create an empty array called simcorr, which we'll use to create our simulated correlation. So I'll go ahead and run that. If we come down here and check out sample core we can see that it's the same value that we got up here, just it hasn't been rounded. So then we need to start the randomization loop. And so, we started like we have all of our randomization loops for I in range N. And then we say sim total gas. So again we're selecting one variable. So this could be water, but I'm going to do total. Guess it doesn't matter which one you select as long as it's the same throughout all of your code. So I'm going to take some total gas and I'm going to shuffle it. So I'm going to say MP dot random choice. And then I'm going to randomly draw from again total gas, so making sure it's the same variable.

Our size is going to be n and then replace equals false. So there are two things that are a little bit different here from what we've done in the past. We're replace... we're sampling without replacement. So you need to make sure that you set replace equals to false. We've done that before, but the main change is that we're just going to simulate, we're just going to randomly sample from one variable, shuffle it, and now we're going to recalculate our correlation.

So this is total base water volume dot corr and total gas, making sure that you're using the simulated code here so that you are taking the correlation with our new re-shuffled data set. So we can run this and if we come down here we can print simcorr and see that we've got a lot of different correlation values, occasionally even some negative values. So one of our reallocations led to a negative relationship between total gas and total base water volume.

So that is the randomization. And like we have done before, a lot of times it's easier to then visualize as the next step. So before we can do that, we need to create data frame for sim corr because right now it is a numpy array and ggplot doesn't like to work with those. So we can say simcorr, the columns I'm just going to write as simcorr, so keep the same columns. And then we can say ggplot simcorr DF, and we can do a histogram.

And so our x value is the only one we need which is simcorr, and then I'm going to add a vertical line where the x intercept equals simcorr, get our sample data set. The color is blue, and we will do line type equals dashed. And I'm going to enter that down so it's a little easier, and wrap this in parentheses so python knows it's all one line. And then we can go ahead and run that. And so, here we can see this is our simulated correlation values. So they're centered around zero, and this is our sample one. And so depending on how we framed our alternative, this value is based, either going to be zero, if it's however much is greater than that, or one, however much is less than that. But we have done a greater than test and so we can say print the p-value, and it is just the length of simcorr where simcorr is greater than or equal to sampcorr divided by n.

So we can run this, and see we get zero, which we expected. There is no data above our sample line, which leads us to reject the null hypothesis. And in particular we can say that the p-value is less than the significance level of 0.05, and give exactly what the p-value is. So we reject the null hypothesis in favor of the alternative that the correlation between these variables is significantly greater than zero. And so, that is how you can do a randomization procedure to test the significance of correlation.

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [1]

Try It: OPTION 2 DataCamp - Apply Your Coding Skills

Using the same data as the previous DataCamp exercise, edit the following code to implement a randomization procedure.

1
2
# libraries
import pandas as pd
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

1/0 0/0

Assess It: Check Your Knowledge

Knowledge Check

Correlation One-Line Test

Read It: Correlation One-Line Test

We can also conduct a one-line test for correlation using the stats.pearsonr command from the scipy.stats library. You can read more about the command in the documentation linked here [3]. Below, we demonstrate the implementation of this command in a video.

Watch It: Video - One Line Test Correlation (2:31 minutes)

Click here for a transcript.

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [1]

Try It: GOOGLE COLAB

Click the Google Colab file used in the video here [4].
Go to the Colab file and click "File" then "Save a copy in Drive", this will create a new Colab file that you can edit in your own Google Drive account.
Once you have it saved in your Drive, try to edit the following code to implement the one-line correlation test.

Note: You must be logged into your PSU Google Workspace in order to access the file.

# create some data
df = pd.DataFrame({'x': np.random.randint(0,100,1000),
                   'y': np.random.randint(0,200,1000)})
 
# run the test with alternative = greater
results = ... 
print('Correlation Coefficient: ', ...)
print('p-value: ', ...)

Once you have implemented this code on your own, come back to this page to test your knowledge.

Assess It: Check Your Knowledge

Knowledge Check

Introduction to Linear Regression

Read It: Introduction to Linear Regression

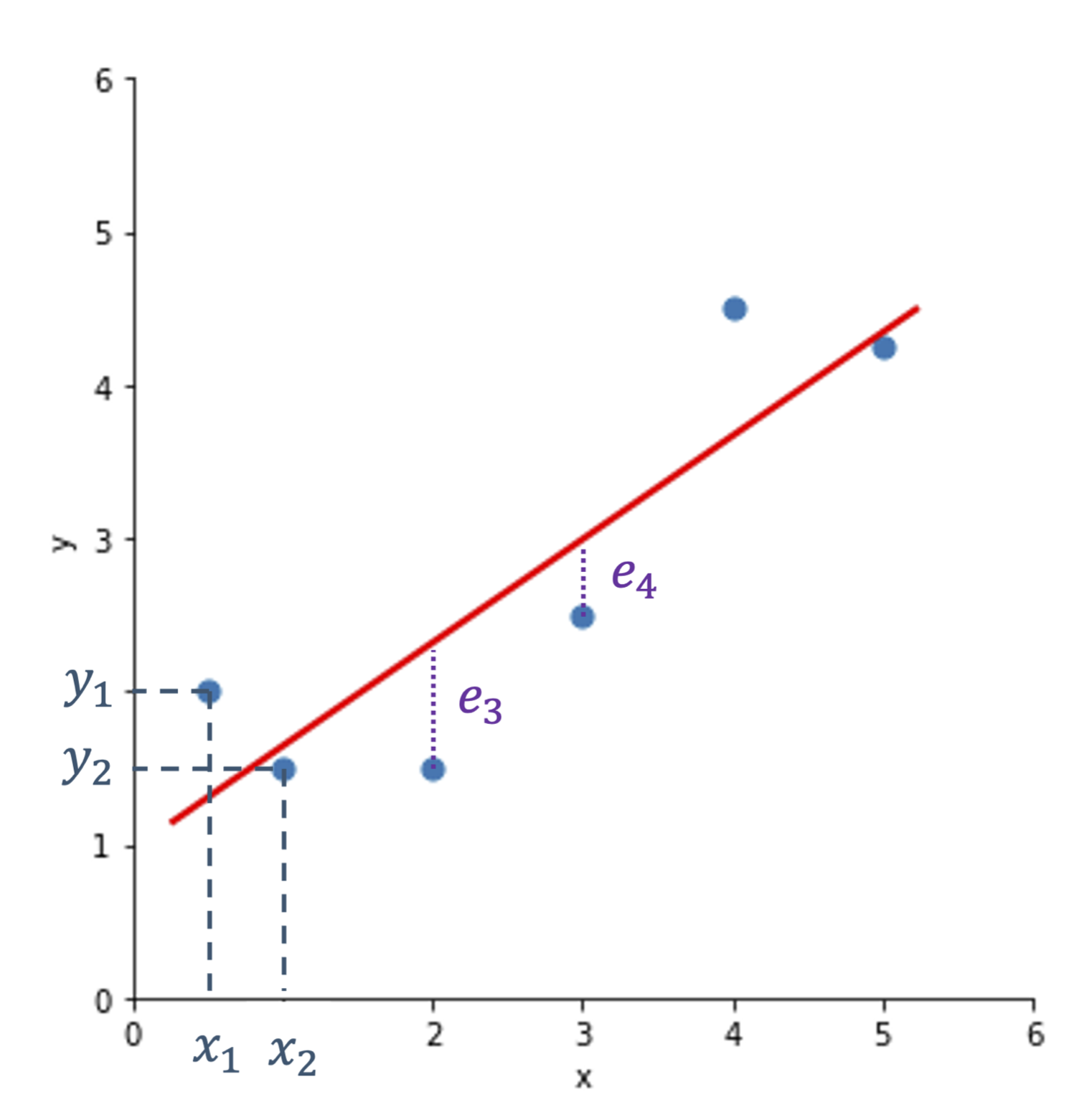
The goal of linear regression is to predict some value y based on the relationship between y and x. In practice, this means we try to find the best fit line to minimize the error. This is shown in the figure below, where we want to find the best line that minimizes the total difference between the data points and the line. The differences are denoted with the letter e. We then define the line based on the slope and intercept, ultimately following the classic equation: $y = m x + b$ , where $m$ is the slope and $b$ is the intercept.

Best Fit Line

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [1]

When working with a sample of data, we usually denote the line as: $y_i = b_1 x_i + b_0 + e_i$ . For a population, we change the equation to include uppercase letters: $Y = beta 1 X + beta 0 + epsilon$

A key aspect of this latter equation is that epsilon is normally distributed (e.g., $N (0, sigma_e)$ ). In fact, the normally distributed error is a critical assumption in linear regression models. Additional assumptions include: (a) a linear relationship between x and y, (b) constant variability in the data, and (c) no outliers present. Examples of how each of these conditions might be broken are provided below.

Figure A:

Click for a text description.

$A = (\begin{array}{ccc} a_{11} & \dots & a_{1 n} \\ ⋮ & ⋱ & ⋮ \\ a_{m 1} & \dots & a_{m n} \end{array})$

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [1]

Figure B:

Click for a text description.

$B = (\begin{array}{ccc} b_{11} & \dots & b_{1 p} \\ ⋮ & ⋱ & ⋮ \\ b_{n 1} & \dots & b_{n p} \end{array})$

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [1]

Figure C:

Click for a text description.

$C = (\begin{array}{ccc} c_{11} & \dots & c_{1 p} \\ ⋮ & ⋱ & ⋮ \\ c_{m 1} & \dots & c_{m p} \end{array})$

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [1]

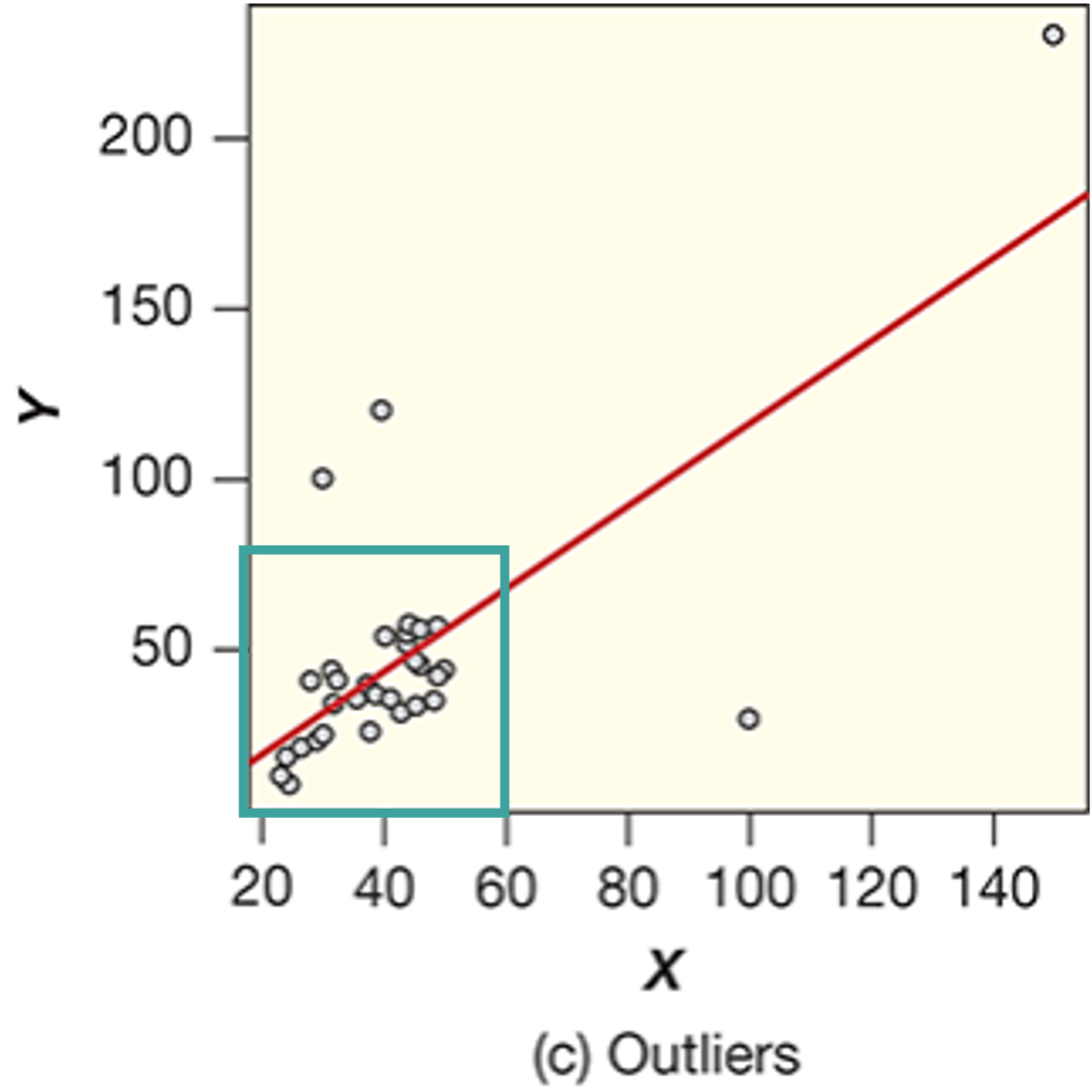
In particular, Figure (a) shows how the first condition (linearity) might be broken. Notice how the pattern is distinctly curved, rather than straight. In Figure (b), the second condition (constant variability) is broken. Here, we see a fan or wedge shape, which indicates that the variance between the y data at x = 20 is much larger than that at x = 10. This means that the variance is not constant, thus breaks one of the conditions for linear regression. Finally, Figure (c) shows the third condition (no outliers) being broken. In particular, there are four likely outliers, which leads to the broken condition. Below, is an example of an ideal example for meeting all three conditions. Notice that the pattern is relatively straight, without increasing variance, and there are no outliers. When conducting linear regression, this is how we want our data to look in an ideal world. Unfortunately, real-world data is rarely this perfect, so we often have to conduct transformations to ensure the model is statistically valid. We will go over these transformations later in the course.

$c_{i j} = a_{i 1} b_{1 j} + a_{i 2} b_{2 j} + \dots + a_{i n} b_{n j} = \sum_{k = 1}^{n} a_{i k} b_{k j}$

Assess It: Check Your Knowledge

Knowledge Check

Linear Algebra Solution of Linear Regression

Introduction to Linear Regression

Read It: Linear Algebra Solution of Linear Regression

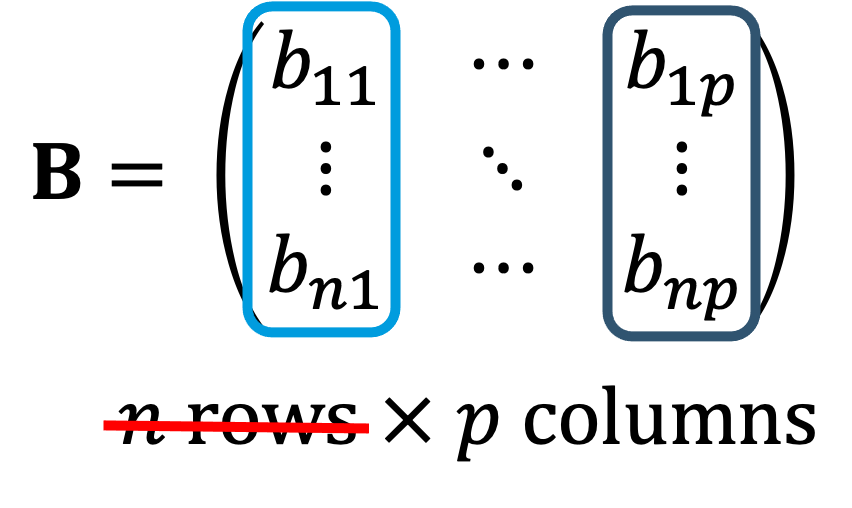
Recall from earlier that linear regression involves finding the best fit line for a given dataset. Traditionally, this best fit line is found through linear algebra. If you have taken a linear algebra course, then you may recall that to multiply two matrices, you sum the products of each row and column together, as demonstrated below.

We will use this concept to find the slope and intercept through linear regression. Below we outline the steps.

Start with a simple linear model for each point in the dataset. $\begin{matrix} y_{1} = b_{1} x_{1} + b_{0} 1 \\ y_{2} = b_{1} x_{2} + b_{0} 1 \\ ⋮ \\ y_{n} = b_{1} x_{n} + b_{0} 1 \end{matrix}$
Convert the series of equations to matrix form. $[\begin{matrix} y_{1} \\ y_{2} \\ ⋮ \\ y_{n} \end{matrix}] = [\begin{array}{cc} x_{1} & 1 \\ x_{2} & 1 \\ ⋮ & ⋮ \\ x_{n} & 1 \end{array}] [\begin{array}{l} b_{1} \\ b_{0} \end{array}]$
Rewrite in matrix notation. $\vec{y} = X \vec{b}$
Multiply both sides of the equation with the transpose of X. $X^{T} \vec{y} = X^{T} X \vec{b}$
Divde both sides by the inverse of X^TX. ${(X^{T} X)}^{- 1} X^{T} \vec{y} = \vec{b}$
Plug the values for b into the equation for the line: $y = b_{1} x + b_{0}$

In the video below, we demonstrate how to implement these steps in Python.

Watch It: Video - Linear Algebra Solution (12:29 minutes)

Click here for a transcript.

All right, welcome back to the video series on linear regression. So in the previous set of videos we talked about correlation and how we can use the hypothesis test for correlation to the term, and the significance of an association. Today we're going to get start getting into actually conducting linear regression. So the correlation can sort of tell us an idea about that association, but the linear regression is what really provides that best fit line and allows us to make predictions based off of that linear model. And so, in this particular video we're going to talk about the manual linear algebra style of doing linear regression. And this is an important base for the next couple videos that will focus on linear regression in Python, because whatever your computer is doing to conduct linear regression it follows the exact same framework that we're about to show in this video. And so, while it may seem a little mathematical and a little abstract, just know that this is the basis for all linear regression that is conducted on any computer program. So with that, let's go ahead and dive right in.

So we are here in Google Colab. And we've got a few additional libraries that we will get to at a later time, but for most of this lecture series I'm actually going to focus on using a data frame that we have talked about when we discuss what spurious correlation is and that is the drowning in nuclear data frame, or data set, that has been published right here. And essentially, this data set has just correlated the amount, the number of drowning deaths in the US with the amount of power generated by nuclear energy. And as we've discussed before, this actually has a very positive, high correlation value. So to demonstrate that as, demonstrate that correlation, I'm going to start with ggplot. So I've called it the data frame df, and I'm also going to add in the AES statement here in the ggplot command like I did in the correlation video. And this just really helps to streamline the plotting process because I no longer need to add an AES statement into each individual plotting command. I can focus on adding in the command specific values, so method, color, and for now, I'm actually going to say se equals false, which says, don't put that confidence interval bands that we often see around the data. So we can see here, we've got nuclear and drowning, and it's a very high, very strongly positive association. But we know from just you know logic, that there is no causal relationship between drowning and nuclear power, just that they seem to have increased at the same rate over time. And so, nonetheless, we're going to use this data set to conduct manual linear regression. And these are going to follow those same steps that we talked about in the lesson itself, but here I'm going to demonstrate how you can do that linear algebra in Python. So, the first step is to create a column of ones, and I'm just going to call it ones, and I'm going to say take a scalar of one and multiply it by the number of rows in df. So, if we print that, we can see that we now have this column of ones alongside our drowning in our nuclear power data.

So then the next step is to extract the x data, and the ones, and form a separate matrix. So when we're doing matrix multiplication and matrix math, we need that y matrix, that x matrix, and then we're going to be solving eventually for that beta matrix. And so, to get this x theta, I'm going to create a new sort of list structure where I put my column names, so drowning, and ones, and then I'm going to say x is pd dot data frame, the f calls dot two numpy. So first I'm converting it into a data frame, and then I'm converting it into a numpy array. So then we can print x and so now we can see that this is the same data that we had up here in drowning, but now it's in matrix array form. So then we need to separate out the y data. And that's going to look very similar. This time we don't need to create a column matrix because it's just one value, so we can say pd data frame df nuclear dot to_numpy. And then we can print y.

And so, now we've just got a matrix of our nuclear data. And now that we've got our y matrix and our x matrix, now we can start to solve that equation. So the first thing we need to do is transpose the x matrix. And so I'm using this transpose command from numpy. And I'm just going to create a new variable, XT np dot matrix dot transpose(X) and this is just where we flip our rows into columns, and our columns into rows. So we can see that now instead of being a long data frame, it's now a wide data frame, with the first row being drowning, and the second row being once. And so, then continuing on with this linear regression, we, the fifth step is to multiply X by XT. And so, if you have taken a linear algebra class then you know that you would do this manually by adding and multiplying rows by columns. But in Python, we have this nice command called matmul from matrix multiplication, and we just give it the two values and I called that (XT, X) for X times XT times X. And so, now we can see we end up with a two by two matrix that is the X multiplied by X transpose. And now the next step, step six, is to do that same process but on the Y. So you can sort of imagine the equation in your head. You've got Y equals X times B. And so, if we do something to the X, we need to also do something to the Y, in order to make sure that we're not unbalancing our equation, essentially. So here I'm going to call it x t y and it is np.metmul, x t comma lowercase y, and then we can run that. And so, we've got a two by one matrix on the Y side. And so, now we've got, if you're following the equation, we've got XTY equals XTX times B. So we need to get that XTX to the other side of the equation, and the way that we do that is through the inverse. So when you divide by a matrix you end up getting this inverse. And so, in order to do that, we're still using this numpy, but we're using linalg, for linear algebra, dot in for inverse. So it's XTX.inv and this is just mp.lin.if and then we just give it the variable XTX then we can print that.

And so, then we can see we've still got this two by two matrix, but this is now the inverse. And so, now that we have the inverse, we're ready to move XTX
in from the right side of the equation to the left. And this is how we essentially get our beta values. So now we're dividing X on both sides. So we've done it from the X side, and now we do it from the Y side, which essentially just means multiplying XTX inverse with XTY.

And the result is our beta values, beta naught and beta one. And so, we can see here that we've got this two by one matrix that contains our slope in the first row and our intercept in the second row. And so, through this linear algebra we can come to this conclusion, the results are the beta values. And so, if we take our regression line Y equals MX plus b we can change that to y equals zero point three one three x plus six one four. And this is now our equation of the line that we could use to make predictions for new Y values given X values. And like I said, this linear algebra solution might be a little abstract, but it's a really important base. Because this is what, for the rest of this lesson, will be happening behind the scenes. This is exactly what python is doing every single time we ask it to do linear regression. So in the next several videos, we'll actually get in to some more python commands for making this process a little easier on us.

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [1]

Linear Regression: One-Line Test

Read It: Linear Regression: One-Line Test

Previously, we demonstrated how to implement a linear algebra based solution for linear regression. This solution is actually the basis for most computer-based solutions, including the one-line test that you will encounter more often. This test uses the stats.linregress function from the scipy.stats library. Below, we demonstrate how to implement this command in the video.

Watch It: Video - One Line Linear Regression (4:31 minutes)

Click here for a transcript.

In this video, I'm going to go over the one-line linear regression command that essentially does everything that that linear regression solution just did, but in a single line. And so, I'm going to call this variable, output. And the command here is stats. Then regress with the scipy stats linked here. And so, we just say stats.line regress. We give it our first variable we give it our second variable and then we can just print the output.

And so, the output includes several parts. So we've got slope intercept r value p-value standard error on the slope, standard error on the intercept, and so there's lots of variables here. So we rarely want all of them in particular. We're interested here in the slope, which is just output dot slope and the intercept which is just output dot intercept, so we can run this. And so we can see here our slope and our intercept values. And if we look up here, they are exactly the same. So if I hide some cells and delete, so we can sort of just barely there we can see that there, so here is our manual output, here is our automatic one-line output. And we can see that they're the exact same number. So this is something that you know uses that linear algebra solution comes the exact same answer, but is a lot quicker to implement for us. And then we can also use those outputs. Since they've been stored very nicely in this output function we can use those to make a basic prediction. So let's say we want to predict the nuclear power for a summer in which we had 475 drowning deaths. So we call that xnew.

Our prediction we always call yhat, so this is not the observed data y, but is the predicted version of that data yhat. We can say output.slope times xnew plus output dot intercept. So this is just our equation of a line y equals mx plus b. And then we can print the predicted nuclear power generation. Officially, it is in megawatts. We can run that, and we can see that the predicted megawatt generation is 762 megawatts. If there were 475 drowning deaths, and this is something we could have done with the manual linear regression as well, just change out this output slope to one of to this first beta value and intercept to the second beta value. But for the remainder of this lesson we'll be focusing on these one-line implementations of linear regressions, which as I said are a little bit faster to run.

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [1]

OPTION 2 : DATACAMP

Try It: DataCamp - Apply Your Coding Skills

Edit the code below to implement the linear regression one-line test between the variables x and y. Print the slope and intercept to the screen

1
2
# libraries
import pandas as pd
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

1/0 0/0

Assess It: Check Your Knowledge

Knowledge Check

Hypothesis Test for Slope

Read It: Hypothesis Test for Slope

So far in this lesson, you have learned about a hypothesis test for correlation and have been introduced to simple linear regression. Here, we will go one step further in our analysis to evaluate the significance of the slope of a line. For this analysis, we will return to our one-line linear regression command: stats.linregress. However, before we can start the analysis, we need to define the hypotheses. For a hypothesis test of slope, the parameter of interest is $β_1$ . Additionally, the null hypothesis will always state $β_1 = 0$ , while the alternative will be some inequality (e.g., $β_1 > 0$ , $β_1 < 0$ , or $β_1 not equal to 0$ ). Below is an example of a set of hypotheses for slope, which we will test in the video demonstration.

$H_0: β_1 = 0$

$H_a: β_1 > 0$

Watch It: Video - Hypothesis Test Slope (4:40 minutes)

Click here for a transcript.

Hello, and welcome back to another video in our linear regression lesson. In this video, I'm going to talk about how we can conduct a hypothesis test to test for the significance of our slope value. And so, this is another great way to add sort of a statistical inference aspect to your linear regression analysis. So you can do correlation, you can look at slope, and later we'll get into additional tests that you can do.

So the first thing that we do with our hypothesis test is state our hypotheses. And I have them stated here. So our h naught is beta 1 equals zero. Likely always it's got an equal sign. And in this case, we're always assuming that it's zero. And then we have our alternative where beta naught is not equal to zero. Now alternatively, you could have beta naught less than zero, or beta 1 greater than zero. But here I'm going to do that two-sided alternative where we say that beta 1 is simply not equal to zero. And now, unlike some of the previous hypothesis testing that we have done, there's no randomization procedure for the slope. In fact, we're going to use this linregress function that we did to do our one-line linear regression in a previous video. And so, this we say stats dot linregress and we just give one value or one variable, then the next variable. And we state our alternative. And this time we're doing two-sided. Alternatively, we could do greater or less as long as we follow our alternative hypothesis. Then we can print the output. And this output is what we have seen before, slope, intercept, r-value, p-value, etc. And so, when we're trying to figure out how to respond, what conclusion to draw from our hypothesis test, we need the p-value. That's just what's given here. And so, we can print that in particular, and say output dot key value. We can do it in a print statement like we have before, so print 'p-value' just output pvalue and run that. And so, we get this p-value of 0.001519, which is below the standard significance level 0.05. And so, we can make this conclusion that the p-value is 0.000152, which is below the significance level. Therefore, we reject the null hypothesis in favor of the alternative that the slope is statistically significantly different from zero. And this is interesting, because if you look up here, our slope is barely above zero, zero point three one three. But that is enough for it to be statistically significantly different from zero, because of really how correlated these values are that even a small slope is significantly different than no slope. And so, this is an example of when you might see that small value and think that it can't be that different from zero. But in reality, because of units and because of the correlation between these two variables, it is much statistically significantly different from zero.

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [1]

Try It: DataCamp - Apply Your Coding Skills

Edit the following code to conduct a hypothesis test for the slope between x and y. Print the slope and p-value.

1
2
# libraries
import pandas as pd
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

1/0 0/0

Assess It: Check Your Knowledge

Knowledge Check

R-squared: Goodness-of-Fit

F-Statistic

Let's start by comparing the hypotheses for a one-way ANOVA test (from Lesson 7) to the hypothese for a simple linear regression model:

One-Way ANOVA vs. Simple Linear Model
Hypotheses for a One-Way ANOVA Test are:	Hypotheses for a Simple Linear Model are:
H_o: All population means, μ i are equal for all k categories	H_o: The model is ineffective (at explaining variability)
H_a: At least one μ i is not equal to the others	H_a: The model is effective (at explaining variability)

The concept that links these two sets of hypotheses is that the grouping of data into k categories in the ANOVA is a model. ANOVA looks at the change in mean (of the response variable) over a categorical variable, whereas a simple linear model looks at the change in mean over a quantitative variable. As such, the simple linear model can also use the F-statistic for its hypothesis test:

$F = \frac{MSM}{MSE}$

where the “Mean Square for the Model” (MSM) replaces “Mean Square for Groups” (MSG) in the numerator and has the equation:

$MSM = \frac{SSM}{1}$

This is essentially the same as MSG, with the main difference being that the denominator has degrees-of-freedom equal to 1 because there is only one explanatory variable in the simple linear model ( $X$ ). Similarly, the equation for MSE is modified with different degrees-of-freedon in the denominator to indicate that there are two “unknowns” in the simple linear model: the slope and intercept (the $\beta$ ’s):

$MSE = \frac{SSE}{n-2}$

Thus, the F-statistic is conceptually the same as what we saw for ANOVA in Lesson 7:

$F = \frac{MSM}{MSE}$

The p-value is determined from the F-distribution in the same way as introduced in Lesson 7 as well.

Coefficient of Determination: $R^2$

While the F-statistic above represents the ratio of the variability in the response data that is explained by the model over the unexplained variability (variability outside the model), the coefficient of determination ( $R^2$ ) is the ratio of the variability in the response data that is explained by the model over the TOTAL variability:

$R^2 = \frac{SSM}{SST}$

In other words, $R^2$ gives the proportion of the total variability in the response data that is explained by the model. Thus, it will always be a value between 0 and 1, with larger values indicating a better “goodness-of-fit” of the linear model.

For a simple linear model, $R^2$ can also be calculated by squaring the correlation coefficient found between the explanatory and response variables:

$R^2 = r^2$

Since $r$ is between -1 and 1, $R^2$ is, again, between 0 and 1, with larger values of $R^2$ corresponding to a stronger correlation. Note that this stronger correlation could be either positive or negative, and $R^2$ cannot distinguish between the two.

It is important to emphasize that $R^2$ is only meaningful for LINEAR models, and won’t capture the variability that could be explained by models that are non-linear (e.g., curved, sinusoidal, clustered, etc.).

Tabular Presentation of Simple Linear Model Test Results

Similar to how ANOVA test results can be presented in a table, simple linear regression results can also be presented in a way that compares the sources of variation:

Source of Variation	Degrees of Freedom	Sum of Squares	Mean Squares	F	p-value
BETWEEN	$1$	$SSM$	$MSM$	$\frac{MSM}{MSE}$	Area under F-distribution and greater than F-statistic
WITHIN	$n-2$	$SSE$	$MSE$
TOTAL	$n-1$	$SST$

Watch It: Video - Hypothesis Test Slope (4:40 minutes)

Hypothesis Test Slope

Click here for a transcript.

Hi, in this video, I'm going to show you three different ways to calculate R², the coefficient of determination, using Python. So let's get down to it. The dataset that we're going to use is what we've been using in previous videos: the nuclear power versus drowning dataset. The first option uses the correlation coefficient, or 'corr' here. So we'll calculate it as we've done previously. We'll put in one variable, and the order doesn't matter here. So, we go with drowning, and we'll say 'corr', the function that we have here, and the other variable, in this case, is Nuclear. We'll print this out. We'll say, "Okay, here's our Coefficient, our correlation coefficient, which is going to be equal to this reported value." We'll round it off just so it's not a whole bunch of decimal places, and we see that it's 0.91, so a pretty high correlation. We can find r2 as just the square of that. So we'll say r2 is equal to r squared here, and then we will print that value, so it will be our coefficient of determination, or I could just put r2. We'll go ahead and run that, and we see that it's the square of 0.9081, so, you know, a moderately good r squared value.

Okay, the second option uses the linear regression function, which we've seen previously as well. In this case, we have to import our scipy stats package. We import this as 'stats', and we'll say 'output equals stats.linregress', as we've done before, and we'll have our X variable and our Y, or our explanatory variable and our response variable, here. We'll see what our output looks like. You've seen this before. We've got all these values. The one we want to focus on is our R value here. We'll note that this is equal to our correlation coefficient we have above, and so we can pull that out and square it again. We'll say, print R-squared is equal to output.r value, and we will square this in place. Let's also round this just so we don't get this huge string of numbers. So I'll round that also to three decimal places and go ahead and run that. There we go. We get the same thing, 0.812.

Alright, and then the third and final way is using a new method, which you haven't seen before. This is from the stats models package. So we'll import that here, and we have to say 'import statsmodels.api'. We'll import this as 'SM' for shorthand, so we don't have to write 'statsmodels.api' every time. The way this works is a bit more complicated than what we have in the linregress. First, we'll define our X variable. We could call this anything we want, but it's handy to just call it X, and that is drowning, as we've seen before, and our Y variable, and in this case, it's nuclear. So we have our X and our Y, and then we will define a model using this function. 'OLS' stands for ordinary least squares. This is our simple linear model, and so we're calling this function. What we're going to do here is define the simple linear model. We'll have to give it the Y first and then the X, so different than what we had before. We should get in the habit of saying hasconst=True. There might be some reason for saying this is False, but throughout this course, we should always put in hasconst=True. Okay, and then once we define our model, we'll fit it. We'll say mod, as we've defined above, our model, dot fit, we'll do our fit function, and we'll say print res. I'm saying res for shorthand, being the results. So, results of the fit, dot summary. So we're going to print a summary of this model. So we go ahead and run that, and there we go.

You'll note, wait a minute, we've got a negative R-squared. That's not possible. What's going on here? You scroll down a little bit more. We'll see we just have one line here. This line is the slope for drowning, and what we should see, what we'd want to see, is a second line giving us the intercept. So we need to go back, and we need to define an intercept. The way we do that is by overwriting X. So we say, X = sm.add_constant. 'Constant' is another name for the intercept here, so add a constant to X. Okay, so all we're doing with this function here is adding an intercept term from the linear algebra solutions, essentially adding a column of ones in our matrix. And there we go. We see that our R-squared is 0.812, exactly as what we had before. Furthermore, if we scroll down for our constant, we get the intercept value that we saw before with linregress, 613 and some change. We can go up and check that intercept, 6113, some change. And, similarly, the slope for our explanatory variable, in this case, drowning. Additionally, we get the P-value associated with that slope right here, and the confidence interval. I should say the 95% confidence interval, so the limits being 0.25 and 0.975. So we get a lot of stuff in this output here. We also get the F-statistic associated with, or related to, the R-squared, as defined in the lesson here, and our degrees of freedom. So, a lot of nice diagnostic output to look at here. And then we also get the P-value associated with the F-statistic as well. So basically, the area under that F distribution above this F-statistic value.

Okay, so we'll look at similar input, or I should say, similar output in subsequent videos. But we'll end here for now with our three methods for getting our R-squared. Okay.

Credit: © Penn State is licensed under CC BY-NC-SA 4.0 [1]

The Colab file used in the video is available here [5]. Make sure to sign in with your PSU credentials.

Assess It: Check Your Knowledge

Knowledge Check

Confidence and Prediction Intervals

We've previously seen confidence intervals for the mean and proportion in Lesson 4. We can also construct a confidence interval around our line of best fit; that is, a lower and upper bound within which we have a certain level of confidence (e.g., 95%) that the population mean is contained. Similarly, a prediction interval gives a range that we are confident (to a certain level) contains the prediction at that specific value of x.

95% Confidence Interval for a Linear Model: there's a 95% chance that the MEAN response at a specific x lies within this interval.

95% Prediction Interval for a Linear Model: there's a 95% chance that the response VALUE at a specific x lies within this interval.

The video below shows how to calculate both confidence intervals and prediction intervals in Python.

Watch It: Video - Prediction Intervals (11:59 minutes)

Prediction Intervals

Click here for a transcript.

Hi, in this video, I'm going to show you how to get confidence and prediction intervals for a linear regression model in Python. So, let's get to it. In order to make this work, the key function we're going to use is get_prediction, and this is coming from the stats models package that we imported in the last video when we wanted to get R-squared. So, the command to do that is, import statsmodels.api as sm. Recall that in the previous video, on the previous page, we ran this code to get this output and stored the fitted model in 'res'. We defined an ordinary least squares, or simple linear regression model, using this line here, and then fit the model to the data here. This is the summary of the output. So, this sort of code needs to be run first in order to make the confidence and prediction intervals using the method I'm going to show you here.

So, let's start off with a simple example. If we want to make some predictions, we can then call our object 'res', shorthand for results. 'res', you know, could be anything; this is user-defined. We again define it up in this line in the previous chunk. The key function here is 'res.get_prediction', or just 'prediction', sorry, and the arguments that you give it are the values at which you want to make the prediction. Now, I have to give it two values, let's say one and 625. Now, where I'm getting these values from: one is corresponding to the intercept. So if in this model I am adding a constant here, and thus have this constant line here, I need to give it a one first. This is basically a placeholder for the intercept, and it has to be one. Now, the second value is the value that's going to be substituted for the explanatory variable, in this case, drowning. So, I'm picking 625 arbitrarily because, if you go back up to the data, 625 is, you know, a bit higher than anything else that we've seen in the data. So, I'm saying, okay, let's predict outside of the data here, but really, this could be any value I want.

So then, in our object 'predictions', I'm going to say 'summary_frame', and I'll give it an alpha value. This is my significance level. We'll use our default significance level of 0.05, which would correspond to a 95% confidence interval and a 95% prediction interval. So, let's go ahead and run that. This is the output I get: 'mean'. This value is the prediction of my linear model. So, this is the value that falls on the line of best fit at the drowning value of 625. 'mean_se': this is the standard error about that estimate. Here are my lower and upper bounds of my confidence interval for that mean, for that prediction. And here are my lower and upper bounds for the prediction interval. Note that it doesn't indicate prediction; it says 'observed confidence interval' and 'obs_ci_lower' and 'obs_ci_upper' here. So, it doesn't align very well with the language used in the lesson, but you just have to bear in mind that these last two values are the prediction interval.

Okay, so that's how we can, at a very basic level, get the confidence and prediction interval for one point, one X value. But oftentimes, it's useful to get it for many values at once and to plot that graphically. So, let me show you how to do that for many instances of X, and then we can plot that.

So, let's make a new code cell. First, let's make a new data frame from scratch here, using Pandas' data frame command. Here, I'm going to just make a new set of X values using the range command. Here, I want to span the range of drowning data that we have. So, I'm just going to generally say 400 to 625, and the third optional command I can give to range is a step size. So, this is going to be the values 400 to 625 in steps of one, so 400, 401, 402, etc., all the way to 625, and that'll be stored in this object 'new_df'. The other thing I need to then create is a column of ones that are the same size as what I currently have here. So, I can say make a new column, call it 'constant' or 'const', for example. I could call it whatever I wanted, and this will be a bunch of ones. So, I'm going to have one in the square brackets and then a multiplication. It means replicate the value one, not multiply that value one this many times. So 'new_df.shape[0]', so I'm going to replicate the value of one as many times as I have rows in this new 'df'.

Okay, so let's take a look at what that looks like, just to show that this works as expected. We can look at the first five rows. There we go. So, I have my X values and just ones. Again, these ones are placeholders for the intercept.

So, now that I have those, I can then use 'get_prediction', this function. I can exercise it over all of these values. So, now I give it my column of ones, not just a single one value, and my column of X's, not just the single X value, and I will store the summary of these into a data frame. So, 'summary_frame' again, I need to specify an alpha. We'll use our default alpha of 0.05, and let's see what we have now.

So, there we go. So now we've got the prediction at X values 400, 401, 402, etc. It's not showing those values here, but it's giving us the predictions, confidence intervals, and the prediction intervals. Okay, let's merge this then with 'new_df'. So, we're going to override 'new_df', which has the X values in it, using our 'pd.concat' command. And so, I'm going to take our existing 'new_df', and I'm going to just append on these predictions. I need to say axis equals one so it does this over the columns, and we'll see what this looks like.

Here, there we go. So now I have the X values in there as well. Okay, let's visualize. We'll import good old Plotnine. Cut this backwards, sorry. This should be 'from plotnine', where we'll import all the commands. And then we can start with our initial data frame that has the data in it, and we'll just start by plotting those points. So, our X was the drowning, and our Y is the nuclear, and let's see what that looks like. Okay, so there's our scatter plot, just the data points. We can use 'geom_smooth' to conveniently make not only our line of best fit but also our confidence interval. We can give it the aesthetic, and then we'll give it a line color. And we can say our method will be 'lm', or linear model. We'll use, we'll say 'se = True', use the standard error method, level 0.95, 95% confidence interval, and we'll fill it with red as well. See what this looks like. There we go. So, there's our 95% confidence interval and our line of best fit. So, the red line is our line of best fit, and we have a 95% confidence interval. And then, this thing is, this doesn't give us our prediction interval. So, we had to calculate that manually. We don't have a convenient built-in function in ggplot to make that prediction interval. But what we can do is we can reference our 'new_df', which has the prediction interval information in it, and so we just have to plug in this new data frame here. So, we're not borrowing from this data frame that we put in ggplot; we have to give it this new data frame. And we'll specify our aesthetic now is a little bit different. Our X is the X column in that data frame, and our Y would be the 'obs_ci_lower' or the lower limit of the prediction interval. And let's give this some colors to differentiate it from red. We'll give it a blue, and let's say, linetype = 'dashed', just to differentiate a little bit more. And we also have to, of course, give it the upper bound too. So, we'll just copy and paste this line and change 'lower' to 'upper'. And there we go. There's our 95% prediction interval in blue. You'll note that it extends a bit beyond what we have in red here. That is because of this line here, this range I said 400 to 625. Let's see, it's going from 400 to 625 here. When I use the 'geom_smooth' command, it automatically limits itself to the limits of the data. But if I wanted to extend the line of best fit and/or the 95% confidence interval to the same limit as the prediction interval, instead of using 'geom_smooth', I can just use 'geom_line' with the 'new_df', because all that information is contained in here too. I just need to give it the right Ys, change the colors how I want, and so on so forth.

Okay, so that is how to do prediction and confidence intervals in Python. Thank you.

The Colab file used in the video is available here [5]. Make sure to sign in with your PSU credentials.

Assess It: Check Your Knowledge

Knowledge Check

Use the table below to answer the following question:

mean	mean_se	mean_ci_lower	mean_ci_upper	obs_ci_lower	obs_ci_upper
8466.215372	5258.166436	-2411.130644	19343.561387	-38519.240164	55451.670907

Transforming Non-Linear Data

Read It: Transformations

Recall from earlier in this lesson when we discussed the conditions that need to be met for linear regression to be a statistically valid technique. Those conditions are: (a) linear shape, (b) constant variance, and (c) no outliers. If any of these conditions are broken, the linear regression model will not be considered statistically valid. In these cases, it is often possible to transform the data so that we avoid breaking the conditions. For example, in the figure below, we should a plot that breaks the third condition (no outliers). If we want to conduct linear regression on this data, it may be helpful to filter the data so that we only focus on the data in the teal box. Be aware, however, that once you make this transformation, any conclusions are only valid for the data inside the teal box! You cannot extrapolate beyond the box, as at that point, the linear regression will no longer be statistically valid.

Subset Transformations

Another common transformation is the log-transform. Here, we calculate the logarithm of the data and use that transformed variable in our linear regression analysis. This can be particularly helpful when the data breaks the first condition (linear shape) or the second condition (constant variance). However, similar to the filtering transformation, you need to be cautious that any conclusions drawn from the updated linear regression are only valid for the transformed data! Below, we demonstrate how to use transformations to improve modeling with linear regression.

Watch It: Video - Transformations (12:17 minutes)

Click here for a transcript.

In this video, we're going to talk about some transformations and demonstrate how you can use these transformations to avoid breaking some of those linear conditions that we talked about earlier. So with that, let's go ahead and jump in.

So in this lesson we're going to use the RGGI data that we used during the Anova lesson. So, I've already got the data loaded and ready to go. So we can jump right in to linear regression. And so, as we start off most things, I want to start off with a plot. So I'm going to do df_merged, which is what I call that data frame, and then just do a point plot, so, x. We're going to do NOx_Base and compare it to NOx_RGGI. I forgot my y equals. And so, this is what the NOx_base in NOx_RGGI data set looks like. So it sort of follows this linear, but then there's all of these over here. And maybe we can classify those as outliers, but I think more likely that this is breaking our constant variance rule because this is a very obvious fan shape. Even though there's nothing really here, this is sort of the outline of a fan. And so, it probably is not the best linear model. We can go ahead and find out. We can say smf.ols, and we can do NOx_AGGI tilde NOx_base. Our data is the F merged. We need to specify has const equals true and I'm going to tack on the fit right onto the end. So then we can print results dot summary and see how the model is actually doing. So it's not terrible, r squared 0.748, that's surprisingly good given all of this out here. But nonetheless, this banding shape clearly breaks our constant variance rule.

And so, even though the linear regression is good, and in terms of the r squared technically it's not statistically valid. So, it would be better if we did a transformation, perhaps, in order to ensure that this that this linear model can be considered statistically valid. And so, what we are going to do is we're going to do a log transform in the hopes of remedying that increasing variability. And so, we can say merged log 10 NOx_base it's just NP dot log 10 BF merged NOx_base. And then I'm going to just repeat that but changing base to RGGI. And so, here we have this. We do get a warning that we encountered a divide by zero, but it didn't stop it from running. And so, we can just sort of move on. See if anything else causes an error, because it could have just created nan's that won't necessarily be bothersome. And so, if we go back and do our geom point plot, this time plotting log 10 and NOx_base and log 10 NOx_RGGI.

We can look at this, and we can say that the variance is no longer increasing, like there's no obvious fan shape. In fact, most of them are now clustered around an even stronger center line. These points out here, maybe now they can be considered outliers. We can't be sure though until we test it. But so far, it looks like our transformation did successfully reduce our variance. Now we just need to make sure we're not breaking another one of those rules, which is no outliers. So, in order to do that, we could do our IQR method and quickly calculate that. But I'm just going to do the visual method. So technically, the geombox plot that we use, it calculates outliers for us. And so, we can just say x equals zero. So this is the one where we need to sort of provide that weird x value, just needs to be any constant. So, x equals zero is common. And then y is log 10 NOx_base.

And so, in the base value there's no outliers. If there were, we would see these little stars up here, right? But we don't have any, so this is a good indication that there's at least no outliers in the base data. I'm going to come down here and paste that same code, change the suffix to RGGI. And there doesn't appear to be any outliers here as well, so in that case our newly transformed data is no longer breaking the increasing variability law, and it's not breaking the no outliers rule. So we are good to go, to do a regression. And so, I'm going to call this regression results 2. But we're still using the linear regression command OLS, but now we are regressing the RGGI log theta with the log theta of base. And again, data is merged df as const is equal to true. And then we can do the fit at the end. Then we can print results to dot summary, and run this... had the wrong order, df underscore merged.

And so, now we get this read, this error, and all it's telling us is that SVD did not converge. So we're having a lack of convergence, and the reason we keep this error in our demonstration is because it's a very strange error but it's very common with log transforms. You wouldn't know it from this SVD did not converge, but what is really being caused by this is the same thing that we got a warning about up here. We ended up with a zero in the log 10 data, which actually creates negative infinities for our data frame. It doesn't matter for the plotting, the plotting will just ignore those values. But it does matter for the actual regression.

So I'm going to leave this in here so that when you see this code you can recognize this error, and just be aware that if you do run into this that this is to go back up, make sure you check to see if you got that warning saying that you divided by zero. And then all you need to do is remove the negative infinities. And so, in order to do that, I'm just going to override the df_merged. And I'm going to say I want to keep df_merged, and just do two conditions, the first is where df_merged dot log 10 NOx underscore RGGI is not equal to negative np dot inf. So this is how we define infinity in Python, is np.inf, and specifically, we want to get rid of the negative versions and we want to get rid of those same values in our base code. So this is saying keep everything except where log 10 NOx_RGGI is, keep everything where this is not equal to negative infinity. And we're log 10 NOx_base is not equal to negative infinity, so we run that. I'm going to come up here, and grab the same regression line to avoid overwriting our previous results. I'm just going to change that to results three. And now we can see that it's running. And in fact, we've got these really high r squared values. So even though our linear regression, if we go up here, 0.748, not terrible. But now with this log transform we're up to close to 0.9, which is an incredible r squared. Our val, our model is now explaining 90 of the variance in the data. It's just important to remember that if we use any of these coefficients that they're on the log transform of the data and not on the original. So if we wanted to make a prediction, for example, we could do that. But if we wanted to apply it back to the original data we'd need to undo the log transform and just figure out what that real value is at that point.

Try It: DataCamp - Apply Your Coding Skills

Edit the following code to first do a log transform of x and y. Then, run linear regression using the statsmodels.formula.api library,

1
2
# libraries
import pandas as pd
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

1/0 0/0

Assess It: Check Your Knowledge

Knowledge Check

Logistic Regression

Read It: Logistic Regression

Occasionally, you may encounter a response variable that is categorical, rather than quantitative. In this case, you can conduct logistic regression instead of linear regression. Through logistic regression, you can conduct a form of regression on a binary variable (e.g., 0/1 or yes/no). Below is a figure that shows a dataset that could be used in logistic regression. In particular, the aim of logistic regression in this case would be to find the curve that separates the "yes" points from the "no" points, based on the input data (e.g. TotalGas and TotalBaseWaterVolume).

Logistic Regression

Mathematically, logistic regression works be defining a response variable with two options: Y = 1 for "yes" and Y = 0 for "no". Then the model tries to predict p, the probability that Y = 1, given the input data. The equation looks like:

$logit (p) = \ln (\frac{p}{1 - p}) = β_{1} X + β_{o} + ϵ$

This results in a sigmoid curve, as shown below, that indicates the probability of success (Y = 1) as a certain value changes. Here, we show how the probability of success increases as the TotalBaseWaterVolume increases, with the actual data in black at Y = 0 and Y = 1.

Logistic Regressions, Part 2

Below, we include two videos demonstrating logistic regression. The first sets the data up, including getting our "yes" and "no" values. The second video is where we implement the logistic regression.

Watch It: Video - Logic Regression Set Up (12:21 minutes)

Click here for a transcript.

In this video we're going to talk about logistic regression, which is a form of regression that allows us to come up with an equation of a line when we only have two options. So, think about a situation where you can either succeed or you can fail. And you still want to know the probability of success or the probability of failure. This is what logistic regression can do, and what we're going to demonstrate today.

So we're here in Google Colab. I've got my libraries loaded, and we're going to be working with the Marcellus Wells and the PA Wells Frac data set that we used during the correlation lesson earlier in this lesson. So, I've already got the data loaded, and I've already gone through our grouping and merging. if you want more details on this process, go back and check out the correlation video where it's explained in detail. Let's move on to the logistic regression. So, logistic regression only works with a binary data set - zero/one, yes/no, success/fail. So, we need to come up with a way to form one of those variables with our data set. And, in order to do that, we need some constraints. So, we're essentially going to compare the cost and profit of drilling a new well in the Marcellus Shale based off of the total water needed to extract the most gas. And so, we have some constraints. The first is that water costs one cent per gallon. The next is that renting a truck to carry that water costs $200, that the truck can hold 6257 gallons, that drilling a well costs $850,000 per 1000 feet, and that there's this base of two million dollars for renting land, paying employees, etc. Now these numbers are not for anything specific, they're just estimates that we pulled out specifically for this demonstration. And so, essentially, the cost of our well is the cost of water, plus the cost of a truck, plus the cost of drilling, plus the cost of just that base load. And then our profit is based off of a price from a couple years ago where gas was selling for five dollars and twenty cents per 1000 cubic feet. And so, that will be our profit. And then we define success as whenever cost is less than profit. So that's what we want. And throughout this, we'll be using a new function called numpy.where, which will allow us to assign a variable based off of a condition. So the first thing we need to do is set up our new variables cost and profit.

So, I'm just going to create a variable cost, and it's just going to follow this function right here. So 0.01 times our total base water volume, which is already in gallon so we don't need to do any unit conversions. And then, we have 200 per truck and we need to figure out how many trucks we need, which is the total base water volume divided by 625. And then we do a plus, and I'm going to put a slash mark here, and that slash allows me to enter down while maintaining the same function line of code. So, if you're doing this on your own and you're just in a single line you don't need to put that slash in, but for me that helps so that you can keep seeing everything that I'm doing. So then the next part of the code is the cost of drilling. So that's $850,000 times merge_df, total depth divided by 1000, and then finally the 2 million base pay. So, that is our cost. And then we can define our profit, which is just 5.2 times our total gas. So, now we've got our our cost and profit, so we need to calculate our successes. So I'm going to create one variable called success, and this is where our numpy.where comes in.

So the command is numpy dot where, and inside this command there's going to be three parts. First, you're going to give the condition comma what to do if true, comma, what to do if false. And so, our condition here is when merge_df of cost is less than merge_df profit. And so, if this is true, we want to write the word yes into that particular row. Otherwise, we want to write the word no. And then I'm going to create a second column which I call successnum, which is just the same statement I'm just going to copy, but instead of words I'm going to change it to the number one and the number zero. And this will become important later on when we need to have numbers to represent our success. And so, if we look at the first five rows we can see that now we've got our cost, our profit successes, and the number of success. Now, this where statement is essentially performing a mixture of an if statement and a for loop all in one. So alternatively, you could do this and essentially that process ends up being a bit longer, but I'm going to go ahead and give a demonstration just for the sake of providing contrast. So we would have for i in the range of merge_df. So, for i, every row in merge_df. Then we need to test that row to see if cost is less than profit. So, we say if merge_df dot iloc, so the i throw dot loc in the cost column is less than merge_df dot iloc. Again, the ith column. But in the profit column, so if that is true we need to say merge_df dot iloc I set the ith column in the success, or the i throw in the success column, equal to yes, and then repeat that for the successnum.

So that's if our cost is less than profit. Then we need to do the other statement. So we can say I if, so else if, but combined. I'm going to copy the same basis here because we want to make sure it follows the same process. But instead we're saying if cost is greater than profit, then our success is no, and our success num is zero, and then two backward spaces to end up outside of both the if statement and the loop. And so, we can run this and we can see that it's taking a little bit longer to run. It has to go through every single row, test every single condition. It's telling me that it doesn't like how I've sliced the data. We can come down here and see the same results as we had before, but instead of having two lines of code we've got seven lines to do virtually the same thing. So, either way is appropriate but in this case the where statement does work a little better. And so, then the last thing that we are going to do in this video is to visualize the variables colored by success.

So, I'm going to use ggplot with merge_df. I'm just going to do a point plot, and so our X variable is total base water volume, our y variable is total gas, and then inside the AES statement I'm going to specify a color as being success. And then outside of the AES statement, but inside the point I'm going to say alpha is 0.25, so that our plot points are partially opaque. And so, here we can see our success data where we have some noes down here, and some yeses up here. There's a few outliers, but by and large they do seem to follow this line. So there might be a good model to use this logistic regression, which we will get into in the next video.

Watch It: Video - Logic Regression Modeling (10:45 minutes)

Click here for a transcript.

In this video we're going to actually conduct the logistic regression. So much of what we did earlier was prepping the data that we needed. We got this nice plot, and now we're going to use the statsmodels.formula.api library in order to fit a logistic regression to our data. And there's some information here that you can use to read up on what the logistic regression is doing. And so, I'm going to create a variable called logregmod logistic regression model. The library is nicknamed SMF, and this is, up here you can see that I've nicknamed this library, SMF. And the command is smf.logit for logistic regression. And this is the formula. So we do the successnum tilde numpy.logit total base water volume. And so, this particular model requires that numeric excess value, which is why we had to create both the yes/no version and the zero/ one version. And then our data is merge_df, and I'm going to pack the fit right onto the end of that. And so, then we can print the results. We can say printlogregmod.summary.

And we can run that. And the summary is much like what we got earlier when we did linear regression. We can see a lot of information. It even gives us this pseudo r squared value. So now, technically logistic regression isn't linear, and so a correlation coefficient would equal zero, r squared would equal zero because we can't apply those variables that measure to non-linear functions. However, what
this command does in logit is, it calculates a pseudo r squared which is a way to assess goodness of fit for non-linear functions. And so, this can tell us that you know technically only about 11 of our data is being explained by this logistic regression model. So not ideal, but still a good exercise to do.

So now that we have the model ready we can use that fitted model to make predictions. And so, I'm going to create a new variable called log10x, which is just going to use our linspace command. Start from four, end at eight, and add as many data points as there are in merge_df. And then I'm going to create a predictions variable which is just our logregmod dot predict, so slightly different function. And there's this variable called exog, which is just another way to say y variable. And so, then it is a little bit funny, it needs to be in a dictionary and it needs to have some connection to the original data set. So, I'm calling it TotalBaseWaterVolume, which is what our original data is. And that's also why up here I said log10x total base water volume, instead of our... instead of creating a new column for the log total waste base water volume, just so that these two values can be the same. But then we can print predictions. And so, we can see here that now we have these predictions for our optimized variable log10x.

And so, then we can actually go in and visualize that data. And so, we're going to start with visualizing the actual prediction. And so, we're going, our actual data... sorry, we're going to say ggplot merge_df geom_point log10water, which is a variable that was created. That is just the log transform of the water variable. And then our Y is again going to be our successnum. So we want it to be in our successnum.

So, this is not how the plot is supposed to look. And I believe that it is because I forgot to do my AES statement, so it didn't know what to do with X and Y because that's not a normal inclusion outside of the AES statement. So, let's run that again and there we have what we actually would expect. So we've got success rate, and we've got log10water here. And so, we can see that there was some successes over here, but not as many. And a lot of successes over here, but there's still a lot of failures at this higher range too.

So this is the original sort of data and now we want to add in our logistic regression curve, which is going to give us the probability between these values. So, in order to do that, we need to first create new variables that are in our data frame because ggplot doesn't like to work with non-data frame values. So we can create an equate or a variable log10x, which just includes our log10x values up here, as well as a predictions column that just contains our predictions. And then I'm going to come up here, grab the same plot, and we're just going to add to it. And so, we can add geome line AES.

And so here our x value is going to be log10x. Our y value is going to be predictions, and then I'm going to add a color blue. I'm going to make it a little bit bigger, so do a size two. And then I'm going to add on to that and add a y label. So this is not something we have done too much, but technically what the y value, y-axis is showing is the probability of success. So technically, although we're plotting successnum and later predictions on the y-axis. What it's actually telling us is probability. So this is a little bit more descriptive, and so here we can see this idealized curve as it goes up. So this is our actual data, but it's even. Though, there's some data points over here. What the logistic regression is doing, is saying that this has to fit some sort of S curve. And so it's more likely to be a failure on the low end with these being some outliers, then it's more likely to be a success on the high end with some of these being. And so, this is ultimately the result of a logistic regression so that then we could come in and say that, you know, at log106, so that's of water, you know. Sometimes there were failures and sometimes there were successes, but if we come up to this curve and start just estimating over here it's about just over 0.25. So maybe 0.3. So there's still a 30 chance of success. So it's on the low end, whereas once we get up to sort of this inflection point, we start to see higher chances of success for the higher amounts of water.

Try It: DataCamp - Apply Your Coding Skills

Edit the code to run a logistic regression model. Your response variable should be the pre-programmed "success" variable and the explanatory variable should be the pre-programmed "x" variable.

1
2
# libraries
import pandas as pd
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

1/0 0/0

Assess It: Check Your Knowledge

Knowledge Check

Summary and Final Tasks

Summary

In Lesson 8, you have learned about applying linear regression to a dataset. Linear regression allows one to quantitatively asses the relationship between two quantitative variables. One can use such an identified relationship to make predictions of the response variable, given a value of the explanatory variable. Lesson 8 is generally ordered by the tasks that one would want to perform in doing linear regression:

Measure and Test for Correlation and Slope: if there is little to no linear relationship between the two variables, there is no point in proceeding further.
Measure Goodness-of-Fit: Does a linear model fit well? Does it explain the majority of variability in the response? If so, what do you learn about the problem by examination of the slope and intercept?
Make Predictions: Just the prediction alone is not very useful, so make sure to also examine the prediction interval to understand the range of possible values that may arise.

We also covered some transformations that you may need to perform to apply linear regression to your dataset.

Assess it: Check Your Knowledge Quiz

Reminder - Complete all of the Lesson 8 tasks!

You have reached the end of Lesson 8! Double-check the to-do list on the Lesson 8 Overview page [6] to make sure you have completed all of the activities listed there before you begin Lesson 9.

Lesson 8: Linear regression