Overview

This is the second of three very dense lessons on the fundamentals of solar energy. Keep it up! The lessons will lighten up a bit as we transition past these core materials.

The Sun provides us with shortwave band light at the Earth's surface, and the Earth emits longwave band light up toward the sky; but what is the role of the Sky/Atmosphere in the energy balance on Earth, and how does the atmosphere affect the bands of light that we collect and find useful at the Earth's surface? In solar energy conversion systems, engineers and design specialists apply meteorological information, particularly shortwave band irradiation (from the Sun) to inform project development and design, and also to inform daily performance of installed systems. To a lesser extent (for some radiative thermal estimations), longwave band irradiation from the Earth and atmosphere is used, but the main driver for our SECSs is the shortwave band.

Applied solar energy workers need to use the same science as those working in the field of Meteorology. The shortwave band of light can be collected via ground detectors (pyranometers/pyrheliometers [1]) or from satellites (GOES East [2], GOES West [3]) to probe and diagnose the behavior of light interacting with the atmosphere and the surfaces of Earth over time. Satellites in orbit have instruments called radiometers [4] to detect and measure the intensity (brightness) of the light scattered back to the satellite. Satellite images of visible light display the shading from clouds, the cloudiness of the Earth's surface, and features such as smoke emerging from large forest fires or volcanoes spewing ash. The signal is a measurement of electromagnetic radiation, both the intensity of the light from the Sun, and the ability of the particles or surfaces to reflect that light back up to the radiometer. Think about what determines the brightness of the light that reflects (is "back-scattered") up to the satellite.

We will start with the concept of electromagnetic radiation, including some important bands of electromagnetic radiation invisible to the human eye. We will also point out ways that a meteorologist and climatologist collect and interpret satellite or radar imagery derived from electromagnetic radiation.

As a preview to Lesson 3, please review the learning objectives on the next page to get an initial sense of the overarching goals that encompass this stage in your forecasting apprenticeship.

At the end of this lesson, you should be able to:

• identify the seven key properties of sunlight;
• differentiate between technical air mass for lab/field-testing and meteorological air masses;
• explain the concept of climate regimes;
• apply clear sky models (REST2 or Bird Clear Sky) to a location and compare the result to real measured data;
• identify the contributions that relate to the solar resource other than the sun (clouds and ground albedo);
• explain Taylor's hypothesis and how it relates to solar intermittency (moving clouds).

What is due for Lesson 3?

This lesson has two learning activities and will take us two weeks to complete. Please refer to the Course Calendar in Canvas for specific timeframes and due dates - those can vary from semester to semester. Specific directions for the assignments below can be found further within this lesson.

Lesson 3 Assignments

Required Reading:	J.R. Brownson, Solar Energy Conversion Systems (SECS), Chapter 3 - Laws of Light (review) J.R. Brownson, Solar Energy Conversion Systems (SECS), Chapter 5 - Meteorology: the Many Facets of the Sky J.R. Brownson, Solar Energy Conversion Systems (SECS), Chapter 6 - Sun-Earth Geometry (Moments, Hours & Days section) C. A. Gueymard (2012) Clear-sky irradiance predictions for solar resource mapping and large-scale applications: Improved validation methodology and detailed performance analysis of 18 broadband radiative models [5] Solar Energy 86, 2145-2169. J. Rayl, G. S. Young, and J. R. S. Brownson (2013): Irradiance co-spectrum analysis: Tools for decision support and technological planning [6] Solar Energy 95, 364-375.
Optional Reading:	Bird and Hulstrom (1981): Simplified Clear Sky Model for Direct and Diffuse Insolation on Horizontal Surfaces, Technical Report No. SERI/TR-642-761, Golden, CO: Solar Energy Research Institute Meteorology for Scientists and Engineers, 2nd ed. by Roland B. Stull (Chapter 7). J.R. Brownson, Solar Energy Conversion Systems (SECS), Chapter 8 - Measure and Estimation of the Solar Resource
HOMEWORK:	Learning Activities Four Laws of Light - due by the end of the first week Clear Sky Model - due by the end of the second week
YELLOWDIG:	Discussion Topic 1: Climate Regimes Discussion Topic 2: Atmospheric interactions - clouds, aerosols, molecules
QUIZ:	Quiz Assignment: Laws of Light and Climate Regimes (see Canvas) - due by the end of the first week

Questions?

If you have any questions, please post them to the Lesson 3 General Questions thread in Yellowdig. I will check these forums regularly to respond. Feel free to go through the comments and post your own responses if you are able to help out a classmate.

Radiometry

For solar resource assessment, radiometry (the measure of electromagnetic or radiant energy) is more valuable than thermometry (the measure of temperature). Solar energy is comprised of the shortwave band of light found between 250-2500 nanometer wavelengths of light ($1 nm={10}^{-9}m$ , or one billionth of a meter). Within the solar field, we measure the shortwave band in terms of irradiance, as W/m² (Watts per square meter, a flux of light per receiving area). If we group irradiance over a block of time, say an hour, we call the measure irradiation, in units of Wh/m² (Watt-hours per area, similar units to electrical energy measure).

Traditional silicon photovoltaics collect energy for electricity production from wavelengths <1100 nm. Other systems like solar hot water panels will collect almost all of the spectrum from the Sun. In fact, almost all of the opaque surfaces about our environment (buildings, roads, water) tend to absorb strongly over the entire shortwave range (leading to an increase in temperature!).

And yet, our wonderfully adaptive human eyes only capture the tiny visible band from 380-780 nm. Thanks to the complex feedback systems from our irises, lenses, and eyelids, eyes can adapt well to extreme conditions of bright or dim lighting but cannot be used to quantitatively gauge irradiance conditions that energetically drive our buildings and photovoltaic systems. Our eyes impart important information, but because they are highly sensitive and adaptive systems, our eyes cannot be used to reliably distinguish and evaluate the solar resource (bare skin may actually be a better receptor for the shortwave band on days that are not windy).

Notice that the "visibility" of a photon is really limited only by the type of detector being used. Let's review the distribution of photons across the electromagnetic spectrum, and then we will discuss types of photon detectors beyond the rods and cones in our eyes. As a reminder, 1 micrometer wavelengths (also called 1 micron wavelengths) are equivalent to 1000 nanometer wavelengths (by unit conversion). It is often easier to use units of nanometers (nm) for the shortwave band, while using units of micrometers (um) for the longwave band. Either will work, but it is helpful to be aware of the relationship.

Now, let's zoom in to the shortwave and longwave bands important to SECSs. Wavelengths are expressed either in nanometers (nm) or micrometers ($\mu m$, also called microns). For wavelengths greater than 380 nm, electromagnetic radiation transitions from the ultraviolet (UV) to the violet visible range for the human eye. As we will observe in the Granqvist figure below, the red visible range ends for wavelengths greater than 780 nm (to the human eye). Notice how the "infrared" crosses over both the shortwave and longwave bands of light.

• SECS have a different operational "grouping" of bands than traditional spectroscopy or remote sensing. Get used to shortwave and longwave bands, as we describe below.

Video: Temperature and Wavelengths (0:57)

All objects glow with energy in proportion to temperature. As temperatures increase, the wavelength oscillations become shorter and the density of photons measured is effectively increased. So, the light becomes more intense (more photons), and each photon is packed with more energy.

Most photons are emitted from a thermal surface, where the constituent atoms are vibrating in the material (this means: temperature). Every material has a thermal property, and hence "everything glows." This concept works well for something called "blackbody emission" (zero emittance) or "greybody emission" (non-zero emittance) but not so well to describe your standard laser pointer or microwave oven. So, just to clarify all cases, there are also photons emitted from the Sun and from solid state devices that are "stimulated emission" (lasers), which can allow for photon emission from surfaces that are high in energy, but not high in thermal temperature.

First rule of Solar Energy: Light is Directional.

This is our first principle of seven for the behavior of light. So, let's begin with the simple yet important statement: Light is directional. Light, as a photon, is born (emitted) from a surface in many directions and then impinges upon other surfaces, where it is either absorbed, reflected, or transmitted (and refracted). We use that directionality to describe the resource. In the text chapter, we have defined a visual shorthand for light that is emitted, transmitted, reflected (scattered), and/or absorbed by various surfaces.

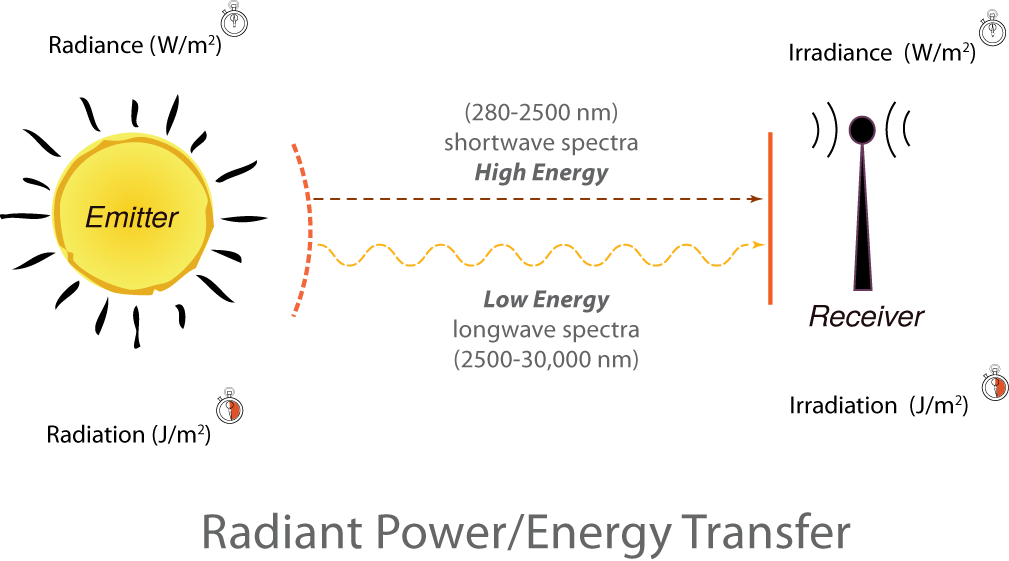
• Irradiance (W/m²): light that impinges upon a receiver surface, interpreted as the instantaneous rate of change in energy (called power, or Watts) per unit area. Remember that one Watt is equivalent to one Joule per second (a rate of energy exchange).
• Irradiation ($J/m^2$ or Wh/m²): light that impinges upon a receiver surface over a period of time, interpreted as the energy (in Joules or Watt-hours) per unit area.
• Radiance (W/m²/sr): light emitted from a surface, interpreted as the instantaneous rate of change in energy (call power, or Watts) per unit area per steradian (a unit of solid angle). If we were to generalize radiance over all exiting directions or angles ($W/m^2$), we term the energy emittance as radiant exitance.
• Radiation (J/m² or Wh/m²): here, using the convention of the field, radiation means light emitted from a surface over a period of time, interpreted as the energy (in Joules or Watt-hours) per unit area. This is a loose operational definition, as "radiation" can mean many different things to different fields of study.

Notice that the "Ir-" instructs us that the light is incident upon a surface. For example, we measure "irradiance" on a pyranometer, because light is absorbed by the device. Also, notice that my choice of "-iance" or "-iation" determines if the light is a measure of rate (as in power: energy per time) or energy (rate integrated over a span of time).

Second Rule of Solar Energy: Light is Spectral.

All objects glow (even the gases in the sky); it is just the intensity and peak wavelength that shifts with respect to their thermal temperature. This brings us to the second of the seven principles of light behavior. Light (e.g., derived from the sun) has a broad spectrum of energies, which are discussed as wavelengths. We tend to group similar wavelengths in the spectrum according to the properties of their emitting surface or receiving surface.

Short Wave Band (250-2500 or 3000 nm)

This is a "group" of high-energy wavelengths of light that are emitted from the Sun (See Light is Directional), comprising the majority of the total energy collected by the Earth's surface or our designed SECS, given the decrease in the light power density with distance to Earth (93 million miles, 150 million km). This bundle of wavelengths of light emitted from the sun includes the ultraviolet (UV), the visible, and the near infrared (IR) sub-bands.

• Shortwave band: The shortwave band of wavelengths is confined from approximately 250 nm to 2500 nm at Earth's surface, because of the Inverse Square Law [9] for light and the nature of our atmosphere as an absorber/reflector of longwave irradiation. Our measurement devices are also limited to measuring this range by the transparency of low-Fe glass covers.

The Sun is effectively the only surface from our surrounding environment that regularly and naturally emits shortwave radiance. We can deliver shortwave band energy to a new surface using a reflector, though, as is the purpose of light concentration onto a central receiver.

Long Wave Band (2500 or 3000 nm - 50,0000 nm)

Long wave band consists of low energy light. The wavelengths of light that are emitted from our skin, from pavement, the sky, ice cubes, and even hot ovens are coming from surfaces that are quite cool relative to the surface of the Sun, right? We are comparing 250-500K surfaces to a 6000K surface. Planck's Law (discussed in the next page) suggests that the distribution of wavelengths will be very different from cool bodies than from extraterrestrial bodies with internal fusion reactors.

The group of wavelengths from cool bodies on Earth is termed the longwave band. This is >2500nm at Earth's surface, but also can be >3000nm if we were to group the wavelengths from space. The longwave band photons are of lower energy, but there is a very wide band of wavelengths included in the group. The longwave band contributes to the greenhouse effect, and keeps our atmosphere comfortably warm. With the addition of CO₂ and water vapor to the atmosphere, we make the sky into a better reflector for keeping longwave energy instead of allowing it to escape into space.

• Longwave band: The longwave wavelengths are found in the range of 2500 nm to wavelengths greater than 50,000 nm, and again our measurement devices are limited to the range of about 30 or 50,000 nm. This second "group" of wavelengths of light is emitted by surfaces significantly cooler than the Sun! This includes the surface of our human bodies, the surface of Earth, and the effective surfaces of Earth's atmosphere (if we were to simplify the atmosphere to two surfaces in a slice of gas and particles).

---

Now, we're going to take a moment to explore the following multiple figure graphic from Smith and Granqvist. There is a lot of information in here, so take your time and revisit it as the class progresses.

• The top graphic, Figure (a), shows the longwave spectrum of radiance (remember, that means "emitted power") from any surface at "ambient" Earth temperatures (-50C to +150C). You see a series of four humped curves that get more intense (bigger), while the peak shifts toward the left (higher energy) as hypothetical surface temperatures increase from -50C to +100C. These temperatures include the Earth's atmosphere, your body, the interior walls of your homes, even a glacier. Remember, all surfaces "glow." This spectral region is the Near-, Mid-, and Far-Infrared, and you may have seen false color images of these emitted surfaces from IR cameras before. The irradiance scales are from 0 to 0.1 W/m²/nm.
• Next, Figure (b) shows the spectrum of Solar light measured just above the atmosphere. The intensity of solar irradiance (remember, that means "received power") at the atmosphere is reduced in proportion to the inverse square of the distance from Sun to Earth. There is effectively only one temperature for the surface of the Sun, and so only one curve, which is far to the left relative to the curves in Figure (a). Also, notice that the intensity of the curve is significantly greater, with a scale from 0 to 2 W/m²/nm.
• Figure (c) shows spectral regions where shortwave and longwave radiation passes through the atmosphere. This is an absorptance spectrum; so, areas where the curve is near one (e.g., 4-8 micrometers) completely absorb the outgoing longwave from Earth and the surrounding atmosphere. Areas where the curve is near zero (e.g., 8-13 micrometers) will allow longwave light to transmit into outer space. The gap between 8-13 micrometers (8,000-13,000 nm) is called the atmospheric window, or the sky window, where the molecules CO₂ and H₂O do not absorb or reflect, and through which a portion of the longwave band can escape. Soon, we will design terrestrial emitters to selectively send energy out the window. This is where longwave radiation from the Earth and Atmosphere leaks radiant energy out into space. Compare Figure (c) with Figure (a) and notice how much they overlap each other.
• Finally, Figure (d) shows a solid line with a peak near 550 nm, demonstrating the relatively tiny region of sensitivity of the eye for detecting photons under daylight conditions (called the photopic state). This is a pretty small energy band, and does not include the behavior of the iris, the eyelids, and the direction your eyes are pointing with respect to your eye lenses. The double peaked dashed line (around 420 nm and 700 nm) is the efficiency of light absorption for green algae, again confined to a tiny region of the whole spectrum. Both curves are normalized fractional scales from 0-1.

---

Third Rule of Solar Energy: Inverse Square Law

Light intensity decreases in proportion to the square of the distance between emitter and receiver. This is called the Inverse Square Law, which applies to solar energy as well as to any other light source. In case of the Sun, the emitted energy flux is 6.33x10⁷ W/m² at the surface of the Sun drops down to 9126 W/m² at the surface of Mercury (d=58 million km), and down to 1361 W/m² at the exterior of Earth's atmosphere (d=150 million km).

As shown in the next figure, the reason for the inverse square law is geometric in nature. As light is emitted from a point, like the Sun at a very large distance, the same quantity of photons is spread out over an increasingly larger area with distance. Area is a spatial term in units of distance squared. This same principle works for ordinary surfaces, as photographers well know.

Mathematically, this process of light “dilution” can be represented by the following equation (which is another form of Equation 3.2 in the SECS textbook)

\[G_2^{} = {G_1}\left( {\frac{{d_1^2}}{{d_2^2}}} \right)\]

where G₁ is the light intensity (or flux) at distance d₁, and G₂ is the light intensity at distance d₂.
If we take G₁ as the radiative energy flux at the surface of the Sun, we can then estimate the radiative energy flux at the Earth’s orbit (G₂) using this equation simply based on the planetary distances. Try to make this calculation with d₁ being the Sun’s radius, and d₂ being the distance from the Sun to the Earth and see what you get. You will have a chance to share your result in the Lesson 3 Activity further in this lesson.

Kirchoff's Law

This radiative transfer law is very important when considering energy balance. It states that at thermal equilibrium, the emissivity ($ϵ$) of a body or surface equals its absorptivity ($\alpha$).

Mathematically, we can conceptualize Kirchoff's law as

$$\frac{E}{E_b}=ϵ=\alpha$$

The radiant energy emitted from a real surface is represented as E (W/m²), while that of a blackbody (a theoretical condition) is given by E_B (W/m²).

Simply put, a surface at steady state temperature will absorb light equally, as well as it emits light. Though light is directional, surfaces exchange photons in both directions.

Planck's Law

This law is generalized to mean that all objects have some internal temperature, and given that temperature, they all glow. Max Planck was able to establish the dependence of the spectral emissive energy of a blackbody for all wavelengths of light ($E_{\lambda ,b}$), given a known equilibrium temperature of the blackbody.

$$E_{\lambda ,b}=\frac{2\pi h{c}^2}{{\lambda }^5[e^{\frac{hc}{\lambda KT}}-1]}$$

Wien's Displacement Law

The Wien's displacement law provides us with expected values for the most probable wavelengths in the Bose-Einstein distribution of blackbody radiation. The law implies that the distribution of photons emitted from a surface at any temperature will have the same form or shape as a distribution of photons emitted from a surface at any other temperature. Mathematically,

$${\lambda }_{max}=\frac{2.8978\times {10}^{6}nmK}{T(K)}$$

Stefan-Boltzmann Law

The Stefan-Boltzmann Law states that the radiative energy emitted by a surface is proportional to the fourth power of the surface's absolute temperature. The Stefan-Boltzmann Law shows that if you were to integrate all the energies from the wavelengths in Planck's Law, you have an analytical solution of the form below:

$$E_b=\underset{0}{\overset{\text{∞}}{{\displaystyle \int }}}{E}_{\lambda ,b}\text{d}\lambda =\sigma T^4$$

where $\sigma$ = Stefan-Boltzmann constant $5.67\times {10}^{-}8W/m^2{K}^4$

Keep in mind that this is for the surface of the emitter. A surface like the Sun will have a very high value for the energy density on the surface, which then decreases in proportion with the Inverse Square Law from the last page (over the 93 million miles distance to Earth's surface).

Wolfram Alpha website [13] is the Google of math and physics. If you want to do calculations on Wien's Law, you type "wien's law" and you will get a calculator for Wien's Law with all sorts of other information. The purpose of this activity is to practice some basic calculations of physical properties of sunlight.

This video below (6 min) presents a short demo on how to use the Wolfram Alpha site. The Stefan-Boltzmann Law is used as an example here, so it provides you with a tip for solving the second problem. 

Submitting Your Work

Prepare a written report with your solutions and upload it to Canvas (Lesson 3 Learning Activity Dropbox) in PDF or docx format. You can use Wolfram Alpha screen shots to present your results for the first two problems (insert the screenshots into your report - don't submit them as separate files). Make sure to present the equations you are using and provide comments to the steps in your solutions.

Grading Criteria

View the Rubric in Canvas by which this assignment will be graded.

Deadline

See the Calendar tab in Canvas for specific due dates.

The action of "reflection" is more appropriately described as "back-scattering" by atmospheric physics, which is why you see that term in the figure of possible paths of light. We also have seen a shorthand diagramming technique from the textbook to describe the life events of ensembles (really big groups) of shortwave and longwave photons.

I would like to pull the concept of photon lifetimes in the following video.

Video: Diagramming Light Intro (2:03)

Each of these phenomena is happening simultaneously, and the next video opens up that discussion.

Video: Light Interactions Descriptive (4:31)

Emission ($\epsilon$), absorption ($\alpha$), reflection ($\rho$), and transmission ($\tau$) can all occur at the same time (in fact it always does). We also know that there is a relationship between light energy balances and temperature. When a receiving surface or material absorbs more energy than it emits, the internal temperature of the material will increase (effectively pumping up the system's energy density). Consider a bright summer day, where your rooftop absorbs much more solar radiation than it emits (or conducts away). The roof surface temperature will rise from just after sunrise to the late afternoon.

Video: Light Diagramming Example (5:49)

The Earth is a vast solar energy conversion system! The atmosphere encasing Earth's land and water mass is a collection of gases and particles that vary in pressure, temperature, and chemistry continuously. If we collectively imagine for just a moment that the atmosphere is a simple cover on top of our main absorber (the Earth), we can begin forming a concept of the atmosphere interacting with electromagnetic radiation across broad bands of wavelengths.

Now, let us consider the optical properties of a single material that reflects light for some bands and transmits or absorbs light for alternate bands, just like the atmosphere represented above. We call the surface of such a material a selective surface, because the light interaction occurs at the surface. A selective surface is non-reflective to some bands of light, while being reflective to other bands of light. The atmosphere is a case study for a selective covering surface between shortwave and longwave bands.

For opaque materials, there is a relation between reflectivity and emissivity (the glow of an object) and between reflectivity and absorptivity.

• A surface that is highly reflective for a certain band of wavelengths is also a surface with a low emissivity.
  • Meaning: reflective materials don't 'glow' effectively.
• In contrast, a surface that has low reflectivity for certain wavelengths of light will have a high emissivity.
  • Meaning: non-reflective materials tend to 'glow' effectively.

We now know the relation for surfaces in optics called Kirchoff's Law of Radiation. When a surface is in thermal equilibrium with the surroundings, the emissivity is equal to its absorptivity at each wavelength ($\epsilon = \alpha$). This allows us to make the same relations among reflectivities and absorptivities.

• A surface that is highly reflective for a certain band of wavelengths is also a surface with a low absorptivity.
  • Meaning: reflective materials don't absorb light effectively either.
• In contrast, a surface that has low reflectivity for certain wavelengths of light will have a high absorptivity.
  • Meaning: non-reflective materials really do absorb light effectively.

We can show the ways in which the Earth-Atmosphere is selective in the relative properties of each to absorb, reflect, and transmit different bands of light.

Video: Solar Case Study (6:47)

We have already described shortwave (280-2500 nm at ground level) and longwave (>2500 nm) bands of irradiation incident upon a surface. The study of optics is that of light-matter interactions, regardless of wavelength. We know that materials like glass are semi-transparent in most of the shortwave band, and materials like pure aluminum are reflective in the shortwave band. We are not so familiar with the way that materials behave in the longwave band, and we often have trouble with materials that are opaque vs. semi-transparent.

Let's review the transmittance graphic that I introduced earlier. This plot has a logarithmic x-axis, so, we can count from 0.2 micrometers (200 nm) up to 1 micrometer wavelengths in increments of 0.1 micrometer. Then, we count from 1 micrometer to 10 micrometers in increments of 1 micrometer, and so on...

We see that from about 0.3 micrometers to about 2.5 micrometers, there is a significant amount of white showing on the plot of the Total Absorption and Scattering, meaning that the absorption and reflection of visible light by the atmosphere is relatively small. In other words, the atmosphere transmits 70-75% of the sun's shortwave light from the top down to the Earth's surface. Along the way, clouds can back-scatter [15] (reflect) some of the visible light into space. In times and places where transmitted sunlight reaches the Earth's surface, then the land, oceans, deserts, grasses, and trees, etc., reflect some of the surface-incident shortwave light back into space (again, with limited absorption along the way).

We also see that from 8-13 micrometers, there is an atmospheric window where the longwave band light is not absorbed or scattered. This is the way that the Earth and the Atmosphere can "leak" energy back into space. If you like, go back to take a look at a similar figure from Granqvist. From which side of the sky window is water vapor absorbing the longwave light, and from which side is CO₂?

Using this example, when incident light (irradiance) is not absorbed or transmitted through the surface and bulk of a material, it is reflected by the surface (the fraction of reflection is called the albedo).

For the good of the engineering community, air masses were "fixed" in 1976 as the U.S. Standard Atmosphere [16] for the ideal clear sky atmosphere in the mid-latitudes of the USA. Yep, and nothing has changed since 1976, right? (cough)

Actually, the American Society for Testing and Materials (ASTM) developed the "Terrestrial Reference Spectra for Photovoltaic Performance Evaluation" so that we could compare and evaluate the performance of our solar technologies, like PV cells and modules. The full documentation of the reference standard is held by the National Renewable Energy Laboratory (NREL AM Standard [17]).

The specified atmospheric conditions are:

1. "1976 U.S. Standard Atmosphere" with temperature, pressure, aerosol density (rural aerosol loading), air density, molecular species density specified in 33 layers;
2. Absolute air mass of 1.5 (solar zenith angle 48.19°s);
3. Angstrom turbidity (base e) at 500 nm of 0.084 c;
4. Total column water vapor equivalent of 1.42 cm;
5. Total column ozone equivalent of 0.34 cm;
6. Surface spectral albedo (reflectivity) of Light Soil as documented in the Jet Propulsion Laboratory ASTER Spectral Reflectance Database [18].

Actually, we are speaking of an air mass coefficient: a relative measure of the optical path length passing through the Earth's atmosphere [19], as described for a fixed moment in time and space. We express the air mass coefficient as a ratio of the direct path of the global shortwave irradiance incident upon a specially tilted surface, relative to the path length for a horizontal surface (optical path oriented vertically upwards as the normal).

AM0

The first thing we need to estimate is what the intensity of the global horizontal irradiance would be just "outside" of our thin covering atmosphere. So, how do we determine the solar energy incident upon the extraterrestrial surface for the Earth-Atmosphere system?

First, we begin with the annual average solar constant, in units of irradiance (recently updated as of 2012! No longer 1366 or 1367 W/m² if you knew that value). The average annual Solar intensity will actually vary according to an oscillation linked to 11-year cycles of sunspots. Given a large number of sunspots, the solar constant will be higher (~ 1362 W/m²) while the value will drop to ~ 1360 W/m² when there are not many sunspots (changes about 0.01%). You can see NASA's Solar Radiation Climate Research Area [20] (accessed Feb 13, 2013).
$$G_{sc}=1361W/m^2$$

Here, G is for Global irradiance, and "sc" stands for solar constant.

Second, we estimate the irradiance of the Sun for the intensity collected on a plane perpendicular to the beam shooting out from the Sun that is also perpendicular to the surface of the Sun (the normal radiant exitance). We would term that "normal global irradiance at AM0" (G_0,n). This would be the equivalent of an estimate at zero cosine projection error, or the angle of incidence is zero. The cosine function in the following Equation delivers the change from zero to one, reflecting the cyclic orbit of the Earth relative to the Sun. The parameter n in this equation is the day number in the year.
$$G_{0,n}=G_{sc}\left[1+0.033\cos \left(\frac{360n}{365}\right)\right]$$

Here, G is for Global, subscript "0" is for Air Mass Zero, and subscript "n" stands for radiant exitance normal to the surface of the Sun (don't confuse it with the day number).

Third and finally, we need to estimate the AM0 irradiance for any given horizontal surface on Earth's surface (G₀). Think about it, a horizontal surface on Earth (or just outside the atmosphere) will be tangent to the curvature of that locale on Earth. We should notice in the following equation that the Earth-Sun relations of declination ($\delta$ ), latitude ($\alpha$), and hour angle ($\omega$) are all included in this irradiance equation for AMO.
$$G_0=G_{sc}\left[1+0.033\cos \left(\frac{360n}{365}\right)\right]\cdot \left[\sin \varphi \sin \delta +\cos \varphi \cos \delta \cos \omega \right]$$

By comparison with our work from Lesson 2, I can point out that the equation is actually multiplying the Equation for G_0,n with the Equation for the solar altitude angle: ${\alpha }_s$ Another way to write this would be $G_0=G_{sc}\cdot \sin {\alpha }_s$ Wow! Lesson 2 really comes in handy!

As a reminder, the relation to find ${\alpha }_s$ is:
$$\sin {\alpha }_s=\left[\sin \varphi \sin \delta +\cos \varphi \cos \delta \cos \omega \right]$$

Consider that the sine of the altitude angle ($\sin {\alpha }_s$ ) is the same as the cosine of the zenith angle ($cos{\theta }_z=sin{\alpha }_s$ ).

• Hourly Irradiation for AM0:

$$I_0=\frac{12\cdot 3600}{\pi }\cdot G_{0,n}\cdot \left[\frac{\pi }{180}({\omega }_2-{\omega }_1)\sin \varphi \sin \delta +\cos \varphi \cos \delta \left(\sin {\omega }_2-\sin {\omega }_1\right)\right]$$

• Daily irradiation for AM0:

$$H_0=\frac{12\cdot 3600}{\pi }\cdot G_{0,n}\cdot 2\left[\frac{\pi }{180}({\omega }_{ss})\sin \varphi \sin \delta +\cos \varphi \cos \delta (\sin {\omega }_{ss})\right]$$

where the hour angle for sunset has been defined in Lesson 2 as:
$${\omega }_{ss}={\cos }^{-1}(-\tan \varphi \tan \delta )$$

AM1.5

The "standard" for testing. The air mass coefficient is defined in proportion to the cosine of the zenith angle (${\theta }_z$): the angle between the beam from the Sun and the normal vector pointing directly up to the zenith of the sky (normal to the horizontal surface).

$$AM=\frac{1}{\cos ({\theta }_z)}\text{[simple, parallel plate]}$$

One needs

• the day number (N),
• the declination ($\delta$),
• the hour angle ($\omega$), and
• the local latitude ($\varphi$) to calculate the zenith angle.

By equivalence, the cosine of the zenith angle is the sine of the altitude angle ${\alpha }_s$ , as we just demonstrated above.

Figure 3.9 illustrates the concept of airmass with respect to a zenith angle of $\mathrm{\theta }={\mathrm{48.2º}}^{}$(AM1.5), or an altitude angle of ${\alpha }_s={\mathrm{41.7º. }}^{}$The hypothetical receiving surface would be tilted at ß = 37º for global irradiance G_t and an angle of incidence of  $$ θ = 11.2º. 

Gueymard has since developed a modified air mass model that will also apply for zenith angles >80°, as the former model tends toward infinity at ${\theta }_z=90°$ .

$$AM=\frac{1}{\cos ({\theta }_z)+0.00176759\cdot {\theta }_z\cdot {(94.37515-{\theta }_z)}^{-1.21563}}$$

Source: Matthew J. Reno, Clifford W. Hansen, and Joshua S. Stein. Global horizontal irradiance clear sky models: Implementation and analysis. Technical Report SAND2012-2389, Sandia National Laboratories, Albuquerque, New Mexico 87185 and Livermore, California 94550, March 2012.

---

Meteorological Air Masses

The Air Masses used in engineering standardization for SECS technologies are not nearly as useful as the real, dynamic air masses that we will use for solar resource assessment.

The sky can be divided up into large volumes with common properties. Air masses are large pancakes of gases and particles (we call them parcels) with common properties of temperature, chemistry, and pressure. Aside from the strong role of clouds, those common physical properties each affect the way in which solar energy intensity will be decreased along the particular path length through the sky. Air mass will affect the way that light is absorbed and scattered, and hence will affect the characteristic behavior of light incident upon an aperture. The changes between air masses are weather fronts, and the study of the regional dynamic dance of air masses and accompanying fronts on a sub-annual basis is called meteorology. When we expand our studies of air mass behaviors to multiregional scales (larger spatial scales) and time scales in the range of decades to millennia, this is called climatology.

I want you to think of an air mass from meteorology as a turbulent pancake that interacts with both shortwave and longwave light, resulting in highly variable irradiance conditions at the ground level, and also for satellite remote sensing in orbit. Irradiance conditions are constantly shifting over a given locale, and we will be in need of effective forecasts of irradiation (over different time intervals) for many SECS technologies.

Seasons: the Sky-Locale Relationship

It is always important to solar energy conversion that we figure time and scale into our understanding. We observe that each location under study is influenced by multiple air masses during different times of the year. In the midlatitudes of North America, we call this periodicity seasons (deep thought, yes). Hence, our solar energy conversion systems are effectively in different locales for each period of air mass dominance.

One locale for your client will be divided up into seasons. For us, each season (a block of time) is like an independent region, different from the next season--and we call these regions climate regimes. In the mid-latitudes we observe four climate regimes, while regions affected by monsoonal swings may have two or three climate regimes.

From the perspective of design in solar energy conversion systems, the skies allowing sunlight through to Philadelphia from December 1 through February 28 exist in a different climate regime from the Philadelphia skies of June 1 through August 31.

Source Regions and the Bergeron Classification System

Recall that the change of irradiation over seasons is due to the tilt of Earth (which leads to our measure of declination). When the Earth is unevenly energized by the Sun, air masses are mobile. Any locale will observe changes in residential air mass behavior over time. Air masses are created in source regions, where the mass acquires its dominant characteristics of temperature and humidity. Then air masses move from the region of origin into new regions. Source regions have been mapped out in Figure 3.11, below, and they will tend to have lighter winds, allowing the air mass to accumulate the temperature and humidity conditions of the accompanying portion of the Earth's surface (the big solar energy conversion device). Hence, areas affected by jet streams will not be regions to create new air masses.

The Bergeron classification system is accepted and used by atmospheric science and indicates the origin locale. This is important information, affecting the quality of the solar resource. Properties of thermal behavior and humidity are conveyed in the Bergeron classification, and the classification has a relatively simple two or three letter coding.

First, air masses are labeled according to their origin above a land mass, continental (c) or above an ocean, maritime (m). Maritime air masses will contain more humidity derived from the underlying body of water. Next, air masses can be grouped into main thermal categories of the site origin: (A, P, T, E). This grouping is largely separated by jet streams and changes in latitude, which of course are each derived by the tilt of Earth relative to the projection of irradiance from the Sun. By coupling the two letters together, we can then map out the source regions for meteorological behaviors across the planet and through the seasonal shifts.

The relation of air mass to monsoon cycles is less used in continental meteorology of North America, but is highly important to solar development in Asia.

Again, air masses are labeled according to the origin of the parcel above a land mass,

• continental (c): low humidity source
• maritime (m), above the ocean: high humidity source regions

Air mass source regions are also grouped according to their thermal characteristics, the thermal generator that is charging up the parcel:

• Arctic/Antarctic (A/AA): A high pressure regime that stabilizes to the far north.
• Polar (P): Very common air mass origin regime for mid- latitude regions of the USA and Europe.
• Tropical (T): Very common air mass origin regime for mid-latitude regions of the USA and Europe.
• Equatorial (E): A high pressure regime that stabilizes near the equator.

The Role of Clouds and Scattering

Clouds have the ability to scatter and even focus light, which means that sometimes a cloud will remove energy from the solar resource on the ground, and other times clouds will collect and focus light that's even more intense than light on the clearest day in your locale. Yet, we know that clouds are ephemeral and dynamic systems in and of themselves.

The albedo is the reflective fraction of light from a given surface, a fractional value from 0-1.

Milk, Albedo and Clouds

Let's consider a jar of clean water (upper left in the photograph), into which one may add a small amount of milk (upper right). Milk is a "colloidal suspension" of solid particles supported/floating in liquid. As such, the solid particles of fat reflect light, scattering the light in many directions like a cloud would do.

In the lower left and lower right corners, the milk concentration has been steadily increased. We can see through the clear glass of water, suggesting that the transmission of visible light from behind the glass to an observer standing behind the camera is high. For the low concentration mixture of milk and water in the upper right, the small amount of added milk has slightly decreased the transmission of light. We can still see the louvers of the window blinds behind the jar, however.

With more milk added to the mixture in the glass on the lower left, the transmission of light was further reduced, and one's ability to perceive the louvers on the other side of the glass was diminished. Finally, adding more milk to the glass in the lower right cut the transmission of visible light to very low levels, and we can't see through the glass.

What is not being transmitted or absorbed is being reflected. Consider this experiment in the context of albedo. The albedo of clean water in the visible sub-band is much lower than the increasing albedos of all three mixtures of water and milk. Of the three mixtures, the glass with the greatest concentration of milk has the highest albedo.

Climate Regimes and Seasonal Fingerprints for Locale

One locale for your client will be divided up into seasons. For us, each season (a block of time) is like an independent region, different from the next season--regions that we will call climate regimes. In the mid-latitudes, we observe four climate regimes, while regions affected by monsoonal swings may have two or three climate regimes.

I want you to think about the way that seasonal (or synoptic) variations in a locale will generate multiple fingerprints. While each fingerprint is different from another in a given locale (translated: winter solar is not like summer solar), additionally, each set of fingerprints is different from another regional set (translated Mumbai monsoons are not like humid summers in Missouri). Every one of our locales for solar design is going to have "cloudy conditions" at some time, and everyone will have "sunny days" at other times. How can we better understand the variety of intermittencies and trends for our locale and synoptic climate regime (our fingerprint)?

Missouri::Maui::Mumbai

This is just a play on words to emphasize something that you probably can guess: these three locations are not like each other!

• St. Louis, MO [25] is representative of the midlatitude climate regime of the intracontinent. Notably, there are four meteorological fingerprints (seasons).
• Maui (Honolulu, HI [26]) is representative of a Pacific island climate regime, affected by monsoons but without a large landmass.
• Mumbai (Mumbai, Marharashtra, India [27]) is strongly affected by monsoonal swings but is located in the low latitudes of the tropics (two fingerprints).

Lesson 3 Discussion in Yellowdig!

We just introduced a totally foreign (yet intuitive) concept of climate regime to our lexicon in solar design. This is a new concept, but an essential one for advanced project development. You can start the discussion by posting what you perceive the meaning of climate regime to be from your personal reading and thought process. You can also comment on any uncertainty you initially found regarding the meaning, the intent, or application of climate regime to a project design, or to long-term project management. Creative interpretations of potential implications are welcome!

Tagging

When you create a post in the Yellowdig discussion space, you are required to choose a topic tag. For Lesson 3 discussions, feel free to use any of the following:

You can tag your post with one or several topics at the same time. All posts and contributions you create are added up to one score at the end of the week.

Importance of interaction

Yellowdig tip: check in the Yellowdig site at least once per day. Commit to making at least one contribution daily – read new posts, ask questions, give your peers reactions and accolades. If reading generates some thoughts, share them, don’t postpone until later. This is a team learning space, so you are also helping others learn by being more active.

Grading

Yellowdig points you earn over the weekly point earning period (from Saturday to next Friday) will count towards 1000 pts. weekly target. But you can go above it (to 1350 pts. max). Yellowdig discussions will account for 15% of the total grade in the course. Check back the Orientation Yellowdig page in Canvas for more details on the points earning rules.

Deadline

There is no hard deadline for participating in these discussions, but I encourage you to create your posts in the middle of the study week (Sunday) to allow others to engage and respond while we are learning specific topics in the lesson. Also, remember that each weekly point earning cycle ends Friday night, so all points accumulated by then will represent your weekly grade, and then you start all over again (it’s like playing a set in tennis..)

In the section discussing components of light, we reviewed the effects of the atmosphere on irradiance. Now, we discuss how to model the transparency of a hypothetical sky that is "clear" of the effects of clouds. Clouds are a major contributor to the reduction of terrestrial irradiance; however, particles in the atmosphere also play a significant role. There are physical properties of the sky that we cannot see with our eyes, but which strongly affect the solar resource on a clear day. As we will see in the reading, aerosols and water vapor present in the atmosphere play an important role in scattering light, and they may be present on "clear sky" days when visible clouds are absent.

Daily or monthly irradiance data is required for proper design of any solar energy collection system. However, this data is not always available. This requires the use of well-designed models to estimate irradiance. Hence, the need for clear sky models.

Clear sky models are used to estimate what is called a clearness index. For a location, a clear-sky model must be properly calibrated to provide an accurate measure for the clearness index. We will be looking at two modeling approaches, the Bird Clear Sky Model (which we can download and use as a spreadsheet) and the REST2 model by Gueymard (which can also be downloaded and run as an executable file--we will not do so here).

Bird Clear Sky Model

The Bird Clear Sky Model was developed by Richard Bird and a number of other scientists at what is now the Department of Energy National Renewable Energy Laboratory. The model requires the following input data

• Solar constant (G_o, W/m²)
• Zenith angle (${\theta }_z$)
• Surface pressure (P, (mbar))
• Ground albedo (${\rho }_g$)
• Precipitable water vapor ([H₂O](cm))
• Total ozone ([O₃] (cm))
• Turbidity at $\lambda =500nm$ and/or at 380nm
• Aerosol forward scattering ratio

Many openly available codes incorporate this model. The output is a "clear sky" estimate for the total or global horizontal irradiance (GHI), direct normal irradiance (DNI) and diffuse horizontal irradiance (DHI, or DIF) across wavelengths from 305nm to 4000nm. The model calculates these conditions for a single point in solar time, given the latitude ($\varphi$), longitude ($\lambda$) and the Time Zone.

REST2 Clear Sky Model

The REST2 model has been found to be most accurate, as we shall observe in our reading. We will only need to explore one method (Bird) for this class, but it is important that a resource professional is also aware of the modern application of clear sky modeling. REST2 accepts atmospheric inputs of:

• Air pressure,
• Precipitable water (also as Temp. and relative humidity),
• Reduced ozone and NO2 path lengths,
• Scattering factors for Ångström’s exponents of scattering [30] (wavelengths above and below 700 nm),
• and Aerosol Optical Depth [31] (AOD).

The REST2 model will then output estimations of diffuse horizontal irradiance (DHI), direct normal irradiance (DNI), and global plane of array (POA) irradiance.

Clouds: the major factor influencing intermittency

Clouds are emergent phenomena within the atmosphere, and strongly perturb the behavior of the solar resource in a given locale. When we do not have a clear sky day in our locale (typical in many locations on Earth), the effects of clouds will strongly draw down the beam component of our solar resource and increase the net fraction of diffuse sky irradiance.

Clouds can develop in environments that are termed active and passive, as well as from updrafts near the Earth’s surface. As we have seen in the reading, clouds have the ability to either scatter and reduce incident light, or to act as a lens at the perimeter, focusing light well above clear sky or even AM0 irradiance conditions.

From the perspective of an observer standing on the Earth's surface, clouds can be classified by their physical appearance. Accordingly, there are essentially three basic cloud types:

• Cirrus, which is synonymous with a "streak cloud" (detached filaments of clouds that literally streak across the blue sky),
• Stratus, which, derived from Latin, translates to a "layered cloud," and
• Cumulus, which means "heap cloud."

Let's review some basic types of clouds. Please do comparative reading between the figure below (with images) and your list of cumuliform, stratocumulus, and stratiform clouds in Ch. 5 of SECS.

Clouds are listed here with images that pop up when you click on the red dots. We see variants of cumuliform clouds, stratocumulus clouds, and stratiform clouds, as noted in our reading.

There are four general classifications of clouds: high, middle, and low clouds as well as clouds of vertical development. The table below summarizes each of these classifications while giving you a sense for the typical altitudes at which their cloud ceilings (the height of their bases) are observed, and the basic chemistry of the clouds (ice and water interact with light in different ways).

General Cloud Classification
Click on images for a larger version

Type of Cloud	Definition	Image
High Clouds	Observed over the middle latitudes. Typically reside at altitudes near and above 20,000 feet. At such rarefied altitudes, high clouds are composed of ice crystals.	[32]
Middle Clouds	Reside at an average altitude of ~10,000 feet over the middle altitudes. Keep in mind that this is an average altitude, so middle clouds can form a couple of thousand feet above or below the 10,000 foot marker. Middle clouds are composed of water droplets and/or ice crystals.	[33]
Low Clouds	Can form anywhere from the ground to an altitude of approximately 6000 feet. For the record, fog is simply a low cloud in contact with the earth's surface.	[34]
Clouds of vertical development	Cannot be classified as high, middle, or low because they typically occupy more than one of the above three altitude markers. For example, the base of a tall cumulonimbus cloud often forms below 6000 feet and then builds upward to an altitude far above 20,000 feet.	[35]

Researchers are now trying to predict cloud behavior with respect to GHI and DNI variation in a given locale. We are still a few years off, but soon we may see solar forecasts that include cloud interference for solar resource assessment.

---

Acknowledgment: Content of this page comes from Meteo 101: Understanding Weather Forecasting; author: Lee Grenci and David Babb.

Clouds (and weather fronts) occur on multiple scales of space and time. These scales contribute to the concept of solar fingerprints or climate regimes. In our reading, we learn about Sir Geoffrey I. Taylor and his work on turbulence theory. Clouds lead to intermittent solar conditions (POA and DNI irradiance) that, in turn,  affect our solar energy conversion technologies, such as PV and building systems.

The intermittent variation of clouds as they affect the solar resource is crucial when solar is deployed as a large-scale farm, or as a large community of decentralized PV arrays on buildings. Variable peaks and valleys of electrical power can be detrimental (costly) to utilities if there are no other ways to store or shave variation on the grid. Now, storage solutions are emerging slowly in research, but right now we need to address the intermittency problem by better understanding the drivers and the basic science underneath those drivers.

Taylor's Hypothesis:

A series of changes in time at a fixed place is due to the passage of an unchanging spatial pattern over that locale. That is, when observing a cloud or thunderstorm passing overhead, the clouds of the thunderstorm floating by are effectively "unchanging spatial patterns" (big blocks of cloud). Put another way, the lateral change in the cloud conditions across regions of the meteorological event (e.g., cloud-sky-cloud-sky-cloud) can be directly connected locally with a variation in irradiance measurement over time (e.g., a periodic measure of dark-bright-dark-bright-dark).

Taylor’s hypothesis states that events that change in time for a fixed place are due to the flow or passage of unchanging spatial patterns over a locale. This is like observing a thunderstorm passing by directly overhead and making the connection to the rate of the clouds advecting with the thunderstorm. Taylor's hypothesis from the 1930s allows us to flip from the Eulerian frame of reference (time sequences) to the Lagrangian frame of reference (spatial changes).

The Eulerian frame of reference: When an observer is stuck in one place, only watching the changing phenomena as it passes by.

The Langrangian frame of reference: When the observer moves with the meteorological phenomena instead of remaining fixed. Imagine a flying carpet floating along with a cumulus cloud moving from one county to the next.

Hence, all scales of time (or frequency) are also spatial scales! Taylor's Hypothesis holds so long as the advective wind speed is much greater than the timescale of the evolving meteorological event being investigated, as is often the case. When you have a lazy cloud day, where the clouds are changing form faster than they move, the time-space connection doesn't hold anymore.

Connecting Scales of Space with Time

By using spatio-temporal scales of cloud features established by Ted Fujita, we can estimate an average translation (advection) speed of 17 m/s for meteorological phenomena. We can then convert the spatial scales of variability into a relevant timescale. Spatial scales associated with power transmission congestion are distances of 25-1000 km. These distances are relevant for meteorological phenomena within time scales on the order of 25 seconds to 16 hours.

Cumulus 2-5 km, which means 10-100 minutes.

Cumulonimbus (including anvil) 10-200 km, which means 1-5 hours.

Cumulonimbus cluster (including merged anvils) 50-1000 km, which means 3-36 hours.

Synoptic (including cyclone waves, short and long Rossby waves) 1000-40000 km, which means 2-15+ days.

If we plot all of these phenomena and draw a line down the middle, we have a really rough estimate of the average advection rate of meteorological phenomena on Earth. Here, we have represented that rate in three different unit scales:

• 17 m/s [easy to remember this one, 17 is a prime number] or
• 1 km/min
• 61 km/hour (or 1470 km/day)
• 38 miles/hour (or 913 miles/day)

As such, we can connect Synoptic, Mesoscale, and Microscale meteorological phenomena between spatial and temporal scales!

Taylor’s Hypothesis “works” when the air in the sky moves significantly faster (advection: wind speeds) than the evolution time of a cloud or a thunderstorm of clouds. So, this approximation breaks down for those days when the cumulus clouds just "hang" in the sky all day.

Clear Sky Model and Measured Irradiance Data

The following readings will be helpful for completing this lesson activity.

Tasks

The goal of this activity is to use the BIRD Clear Sky Model to predict the solar irradiance at a specific time at a specific locale and further compare those predictions to actual irradiance measurements.

These two tasks will be performed for a specific date - July 31, 2007 (in this assignment) for the specific locale - SURFRAD Meteorological Station at Rock Springs, located just outside State College, PA.

In the end, you will need to assess how the modeled (predicted) and measured data fit and provide some discussion on it.

Part 1. Bird Clear Sky Model - Instructions

The Bird model is an old but advanced clear sky model used by solar professionals to estimate clear sky conditions at a locale. The clear sky model for a horizontal surface is the basis for almost all modern comparisons of "ideal skies" to actual skies (with clouds and dynamic light interference effects). You will see what the global, beam horizontal, and diffuse components of solar light should look like when you set the meteorological parameters affecting the sky clearness. The model could also provide DNI (Direct Normal Irradiance), which would show irradiation values higher than the global horizontal values for the mornings and evenings.

• Go to http://rredc.nrel.gov/solar/models/clearsky/ [29] to download the Bird Clear Sky Model. It is a free download, and the tool comes in the form of an Excel spreadsheet. I suggest that you rename the original file for any case study you perform further.
• Study the instructions on the spreadsheet to learn how to use the tool and make a note of the input and output parameters.
• Modify the inputs for the State College, PA, locale. The following parameters can be obtained from the SURFRAD site (see part 2):
  • Latitude 40.72
  • Longitude -77.93
  • Time zone UTC -5
  • Pressure (mbar) - average for the day
  • Aerosol optical depth (AOD)

Note: access the AOD data through this graphical page [36]. Take the daily average as input for the Bird model. In this case, 415nm AOD can be used as a proxy for 380nm AOD input and 500nm AOD data can be used as is.

• You can leave other inputs at their default values
• Expand the spreadsheet (as explained in the instructions) to generate output for the entire year, then extract the data for July 31st (day # 212) and copy values to a separate file.
• Plot global horizontal irradiance (GHI), direct horizontal irradiance (DHI), and diffuse horizontal component (DIF) versus time for the day

The model plot will look similar to the one below. This is what you need to produce.

Part 2. SURFRAD data - Instructions

The SURFRAD site at Penn State collects real-time data for solar irradiance (using local pyranometers) and a number of other atmospheric parameters at 3-minute time intervals. These data are accessible through the Earth System Research Laboratory website [37]. This site provides you with access to data collected at the Penn State location. For each year, you can open the parent directory with .dat files, which are named by the day number. So if you are looking for July 31st, for example, that will be day #212, so check the file psu07212.dat.

Here are the data labels in order that correspond to the numbers in the .dat file (omit 0-value columns):

Year, jday, month, day, hour, min, dt (decimal time), zen (degrees), dw_solar (W/m^2), uw_solar (W/m^2), direct_n (W/m^2), diffuse (W/m^2), dw_ir (W/m^2), dw_casetemp (K), dw_dometemp (K), uw_ir (W/m^2), uw_casetemp (K), uw_dometemp (K), uvb (mW/m^2), par (W/m^2), netsolar (W/m^2), netir (W/m^2), totalnet (W/m^2), temp (degC), rh (%), windspd (m/s), "winddir (degrees, clockwise from north)", pressure (mb)

From this list, you will specifically need: 

dt (decimal time) - your time coordinate for data plotting (Column G in MS Excel) 

dw_solar - Downwelling global solar (W/m^2) = corresponding to Global Hz (GHI) in BIRD model (Column I in MS Excel)

netsolar - Net solar (W/m^2) = corresponding to Direct Hz (DHI) in BIRD model (Column AG in MS Excel)

diffuse - Real downwelling diffuse solar (W/m^2) = corresponding to Dif Hz (DIF) in BIRD model (Column O in MS Excel)

Also, 'pressure (mb)' - the last value in each array of data - daily average should be used for your Bird model input (Column AU in MS Excel).

To treat the data, you can either convert the .dat file to a spreadsheet (see video in Canvas Module 3 how to!) or, if you have programming skills, you can create a script to plot the irradiance data versus time.

Comparison and discussion of the results

• Plot the Bird model data and SURFRAD measured data for GHI, DHI, and DIF types of irradiance on the same diagram. You should get a pretty close match. You may notice by visually comparing the curves, that even on a clear day, the real sky shows dynamic variations in irradiance in the diffuse component.
• Provide a discussion of the results and comment on the possible discrepancies.

Submitting Your Work

Prepare a written report including the following: 

1. Table of input parameters for the Bird model (left side of the Bird spreadsheet)
2. Diagram with irradiance data comparison (Bird model vs. SURFRAD data points)
3. Discussion of results.

Save your report as .docx or PDF and submit to the Lesson 3 Activity - Clear Sky Model dropbox in Canvas.

Grading Criteria

Please see the grading rubric in Canvas

Deadline

See the Calendar tab in Canvas for specific due dates.

Summary

In this lesson, we have learned about the diverse ways in which the atmosphere can interact with shortwave light to affect the solar resource received at the ground by our Solar Energy Conversion Systems. We have observed that the sky has a distinct character derived from air mass source regions, and that the weather has seasonal "fingerprints" that distinguish a single site as multiple unique climate regimes. We further found that a "clear sky" is a fairly complex system of its own, and modeling the clear sky is not trivial. When we finally add clouds to the skies, we see where the real source of solar intermittency stems from. By connecting space and time from Taylor's Hypothesis, we find that we hold additional information on the scales of intermittency to expect in a given locale and for each seasonal climate regime in that same locale.