Lesson 2: Biases and Solutions
The links below provide an outline of the material for this lesson. Be sure to carefully read through the entire lesson before returning to Canvas to submit your assignments.
Lesson 2 Overview
Overview
Biases are fascinating. The frequency standards, the clocks in GPS satellites, run faster than the clocks in GPS receivers, and the clocks in the GPS receivers are much less sophisticated than the clocks in the satellites. During the trip through the ionosphere, the information on the GPS signal appears to slow, and the ionosphere affects L2 more than L1. You might find it interesting that when a GPS signal reflects off a surface before it reaches your receiver, this is called multipath, and, believe it or not, it actually has something in common with a billiard ball (as a billiard ball often bounces off several surfaces before finding its way to the pocket). In this lesson, we will also talk about how GPS surveying is done.
Objectives
At the successful completion of this lesson, students should be able to:
- demonstrate biases and solutions;
- explain the error budget;
- explain the biases in the observation equations;
- describe user equivalent range error;
- identify the satellite clock bias, dt;
- define the ionospheric effect, dion;
- recognize the receiver clock bias, dT;
- describe the orbital bias;
- explain the tropospheric effect, dtrop ;
- identify multipath;
- recognize differencing;
- differentiate between classifications of positioning solutions;
- discuss relative and autonomous positioning; and
- recognize the benefits of single, double, and triple differencing.
Questions?
If you have any questions now or at any point during this week, please feel free to post them to the Lesson 2 Discussion Forum. (To access the forum, return to Canvas and navigate to the Lesson 2 Discussion Forum in the Lesson 2 module.) While you are there, feel free to post your own responses if you, too, are able to help out a classmate.
Checklist
Lesson 2 is one week in length. (See the Calendar in Canvas for specific due dates.) To finish this lesson, you must complete the activities listed below. You may find it useful to print this page out first so that you can follow along with the directions.
| Step | Activity | Access/Directions |
|---|---|---|
| 1 | Read the lesson Overview and Checklist. | You are in the Lesson 2 online content now. The Lesson 2 overview page is previous to this page, and you are on the Checklist page right now. |
| 2 | Read Chapter 2 in GPS for Land Surveyors. | Text |
| 3 | Read the lecture material for this lesson. | You are currently on the Checklist page. Click on the links at the bottom of the page to continue to the next page, to return to the previous page, or to go to the top of the lesson. You can also navigate the lecture material via the links in the Lessons menu. |
| 4 | Participate in the Discussion. | To participate in the discussion, please go to the Lesson 2 Discussion Forum in Canvas. (That forum can be accessed at any time by going to the GEOG 862 course in Canvas and then looking inside the Lesson 2 module.) |
| 5 | Prepare a 2,400 word paper on one topic covered in Lessons 1 and 2. Write on any topic that we have covered and relate it to the work you are doing now or the work you hope to do. | Please submit your paper to the Lesson 2 Basic GPS Paper Drop Box located in the Lesson 2 module in Canvas. View Calendar in Canvas for due date. |
| 6 | Read lesson Summary. | You are in the Lesson 2 online content now. The lesson Summary is the final page of the lesson. |
The Error Budget
The understanding and management of errors is indispensable for finding the true geometric range ρ between a satellite and a receiver from either a pseudorange or carrier phase observation.
Both equations include environmental and physical limitations called range biases.
Atmospheric errors are among the biases; two are the ionospheric effect, dion, and the tropospheric effect, dtrop. Other biases, clock errors symbolized by (dt-dT) and receiver noise, ερ and εφ, multipath, εmρ and εmφ, and orbital errors, dρ, are unique to satellite surveying methods. As you can see, each of these biases comes from a different source. They are each independent of one another, but they combine to obscure the true geometric range. The objective here is to discuss each of them separately.
Here, we see the formula of the pseudorange error budget on the upper portion. As it indicates, p is the pseudorange, measurement equals ρ, rho, the true range between the GPS receiver and satellite. However, as you can see, there are many more elements, errors, or biases that contaminate the pseudorange— the satellite orbital errors, the ephemeris errors, etc.
The time difference (dt-dT) is between the satellite clock offset, and the receiver clock offset from GPS Time, as was mentioned in the previous lesson. There is also the ionospheric delay, the attenuation, of the signal as it passes through the ionosphere. Distinct from these biases are multipath and receiver noise. These two are distinct because, unlike the others, it is difficult to deal with them in a statistical way. Nevertheless, all are part of the error budget.
Directly below the pseudorange formula, you see the carrier phase formula. It also equals true range symbolized by capital phi,Φ. It includes errors that are very similar to those in the pseudorange formula. But one is included that is obviously different. It is symbolized by the capital N followed by the letter lambda, λ. This is the integer ambiguity. It doesn't occur in the pseudorange measurement.
The management of the errors shown in the formulas, the biases, is indispensable for finding the true range from either a pseudorange or a carrier phase observation. In this lesson, we're going to try to understand the source of these errors so that they can be dealt with.
User Equivalent Range Error

The summary of the total error budget affecting a pseudorange from the user's point of view is called the user equivalent range error, UERE. This expression, often used in satellite surveying literature, is the square root of the sum of the squares of the individual biases. See figure above. The UERE is the ranging error between a satellite and the user’s receiver. It can be shown as a distance that includes both the signal in space ranging error called URE (User Range Error) and the user equipment error (UEE).
Some of the biases that make up the UERE such as those attributable to the atmosphere dion , dtrop and satellite orbits dρ increase and decrease with the length of the baselines between receivers. Differential correction techniques can often limit the effect of these errors. Others included in the UERE, such as those due to receiver noise, ερ and εφ, multipath, εmρ and εmφ, do not increase and decrease with the length of the baselines between receivers.
The Satellite Clock
The Satellite Clock Bias, dt
One of the largest errors can be attributed to the satellite clock bias. It can be quite large, especially if the broadcast clock correction is not used by the receiver to bring the time signal acquired from a satellite’s onboard clock in line with GPS time. As time is a critical component in the functioning of GPS, it is important to look closely at the principles behind this bias.
The onboard satellite clocks are independent of one another. While GPS time itself is designed to be kept within one microsecond, 1 µsec or one-millionth of a second, of UTC, excepting leap seconds, the satellite clocks can be allowed to drift up to a millisecond, 1 msec or one-thousandth of a second, from GPS time. They are allowed to drift within this tolerance because the Control Segment doesn't want to constantly tweak the clocks, as this would cause the clocks to deteriorate more rapidly. Although the GPS satellites have been robust, I think it's fair to say that the clocks are one of their more fragile components. Instead, we have the broadcast clock correction in the Navigation Message. This is the correction that the Control Segment provides to the receiver to use to bring the satellite clock in line with GPS time.
Relativistic Effects on the Satellite Clock
Albert Einstein’s special and general theories of relativity apply to the clocks involved here. At 3.874 kilometers per second, the clocks in the GPS satellites are traveling at great speed, and that makes the clocks on the satellites appear to run slower than the clocks on earth by about 7 microseconds a day. However, this apparent slowing of the clocks in orbit is counteracted by the weaker gravity around them. The weakness of gravity makes the clocks in the satellites appear to run faster than the clocks on earth by about 45 microseconds a day. Therefore, on balance, the clocks in the GPS satellites in space appear to run faster by about 38 microseconds a day than the clocks in GPS receivers on earth. So, to ensure the clocks in the satellites will actually produce the correct fundamental frequency of 10.23 MHz in space, their frequencies are set to 10.22999999543 MHz before they are launched into space.
There is yet another consideration, the eccentricity of the orbit of GPS satellites. With an eccentricity of 0.02, this effect on the clocks can be as much as 45.8 nanoseconds. Fortunately, the offset is eliminated by a calculation in the GPS receiver itself; thereby avoiding what could be ranging errors of about 14 meters. The receiver is moving, too, of course, so an account must be made for the motion of the receiver due to the rotation of the earth during the time it takes the satellite's signal to reach it. This is known as the Sagnac effect, and it is 133 nanoseconds at its maximum. Luckily, these relativistic effects can be accurately computed and removed from the system.

The Ionospheric Effect
The Ionospheric Effect, dion
The Earth's Ionosphere is variable

One of the largest errors in GPS positioning is attributable to the atmosphere. The long, relatively unhindered travel of the GPS signal through the virtual vacuum of space changes as it passes through the earth’s atmosphere. Through both refraction and diffraction, the atmosphere alters the apparent speed and, to a lesser extent, the direction of the signal. This causes an apparent delay in the signal's transit from the satellite to the receiver.
Ionized Plasma
The ionosphere is ionized plasma comprised of negatively charged electrons which remain free for long periods before being captured by positive ions. It is the first part of the atmosphere that the signal encounters as it leaves the satellite. The magnitude of these delays is determined by the state of the ionosphere at the moment the signal passes through, so it's important to note that its density and stratification varies. The sun plays a key role in the creation and variation of these aspects. Also, the daytime ionosphere is rather different from the ionosphere at night.

Ionosphere and the Sun
When gas molecules are ionized by the sun’s ultraviolet radiation, free electrons are released. As their number and dispersion varies, so does the electron density in the ionosphere. This density is often described as total electron content or TEC, a measure of the number of free electrons in a column through the ionosphere with a cross-sectional area of 1 square meter: 1016 is one TEC unit. The higher the electron density, the larger the delay of the signal, but the delay is by no means constant.
The ionospheric delay changes slowly through a daily cycle. It is usually least between midnight and early morning, and most around local noon or a little after. During the daylight hours in the midlatitudes, the ionospheric delay may grow to be as much as five times greater than it was at night, but the rate of that growth is seldom more than 8 cm per minute. It is also nearly four times greater in November, when the earth is nearing its perihelion, its closest approach to the sun, than it is in July near the earth’s aphelion, its farthest point from the sun. The effect of the ionosphere on the GPS signal usually reaches its peak in March, about the time of the vernal equinox.

Ionospheric Stratification
For ease of reference, the ionosphere can be said to extend from 50 kilometers to 1,000 kilometers above the earth's surface. It can be divided into the mesosphere and thermosphere, et cetera that are themselves composed of layers: D, E, and F. Neither the boundaries between these regions, nor the upper layer of the ionosphere, can be defined strictly. Here are some general ideas on the subject. The lowest detectable layer, the D region, extends from about 50 km to 90 km. It has almost no effect on GPS signals and virtually disappears at night. The E region, also a daytime phenomenon, is between 90 km and 120 km. Its effect on the signal is slight, but it can cause the signal to scintillate. The layer that affects the propagation of electromagnetic signals the most is the F region. It extends from about 120km to 1000km The F region contains the most concentrated ionization in the atmosphere. In the daytime, the F layer can be further divided into F1 and F2. F2 is the most variable. F1, the lower of the two, is most apparent in the summer. These two layers combine at night. Above, the F layer is fully ionized. It is sometimes known as the photosphere or the H region.
The ionosphere is not homogeneous and unchanging. It is in constant flux. Therefore, it's impossible to have a correction that's static. Also its behavior in one region of the earth is liable to be unlike its behavior in another. For example, ionospheric disturbances can be particularly harsh in the polar regions. But the highest TEC values and the widest variations in the horizontal gradients occur in the band of about 60° of geomagnetic latitude. That band lies 30° north and 30° south of the earth’s magnetic equator.
Satellite Elevation and Ionospheric Effect
The severity of the ionosphere’s effect on a GPS signal depends on the amount of time that signal spends traveling through it. A signal originating from a satellite near the observer’s horizon must pass through a larger amount of the ionosphere to reach the receiver than does a signal from a satellite near the observer’s zenith. In other words, the longer the signal is in the ionosphere, the greater the ionosphere’s effect on it.
Group and Phase Delay
The ionosphere is dispersive, which means that the apparent time delay contributed by the ionosphere depends on the frequency of the signal. During the signal’s trip through the ionosphere, this dispersive property causes the codes, the modulations on the carrier wave, to be affected differently than the carrier wave itself. The P code, the C/A code, the Navigation message, and all the other codes appear to be delayed, or slowed, affected by what is known as the group delay. But the carrier wave, itself, appears to speed up in the ionosphere. It is affected by what is known as the phase delay. It may seem odd to call an increase in speed a delay. It is sometimes called phase advancement. In any case, it is governed by the same properties of electron content as the group delay, phase delay just increases negatively. Please note that the algebraic sign of dion is negative in the carrier phase equation and positive in the pseudorange equation. In other words, a range from a satellite to a receiver determined by a code observation will be a bit too long and a range determined by a carrier observation will be a bit too short.
The Magnitude of the Ionospheric Effect
The error introduced by the ionosphere can be very small, but it may be large when the satellite is near the observer’s horizon, the vernal equinox is near, and/or sunspot activity is severe. For example, the TEC is maximized during the peak of the 11-year solar cycle. It also varies with magnetic activity, location, time of day, and even the direction of observation. In any case it's fair to say that one thing one can depend on is the longer that the GPS signal remains in the atmosphere, the longer its trip through that atmosphere, the greater the effect of attenuation will be. So, one of the things that a GPS receiver ought to do is ignore the signals coming from satellites that are near the observer's horizon. Obviously, as the GPS satellite is low in the sky, the signal is going through a greater atmosphere than it would be when it is directly overhead at zenith. This is one of the reasons why it's a good idea to have a mask angle on the GPS receiver (i.e.15-20 degrees) such that it will ignore the signals that are low, coming in through a great deal of atmosphere. So, no matter what time of year or the time of day, you want to avoid going through the atmosphere and get signals from satellites that are a little bit higher in the sky. It would also be a good idea to try to model the effect of the ionosphere. There's actually an aspect of GPS that allows us to have a pretty good shot at quantifying the effect of the atmosphere on our observations.
Different Frequencies Are Affected Differently
Another consequence of the dispersive nature of the ionosphere is that the attenuation for a higher frequency carrier wave is less than it is for a lower frequency wave. That means that L1, 1575.42 MHz, is not affected as much as L2, 1227.60 MHz, and L2 is not affected as much as L5, 1176.45MHz. This fact provides one of the greatest advantages of a dual-frequency receiver over the single-frequency receivers. The separations between the L1 and L2 frequencies (347.82 MHz), the L1 and L5 frequencies (398.97 MHz) and even the L2 and L5 frequencies (51.15 MHz) are large enough to facilitate estimation of the ionospheric group delay. Therefore, by tracking all the carriers, a multiple-frequency receiver can model and remove, not all, a portion of the ionospheric bias. There are now several possible combinations, L1/L2, L1/L5 and L2/L5. It is even possible to have a triple frequency combination to help ameliorate this bias.
The frequency dependence of the ionospheric effect is described by the following expression (Klobuchar 1983 in Brunner and Welsch, 1993):
Where:
As the formula illustrates, the time delay is inversely proportional to the square of the frequency; in other words, the higher the frequency, the less the delay. For example, the ionospheric delay at 1227.60 (L2) is 65% larger than at 1575.42 MHz (L1), and at 1176.45 MHz (L5) it is 80% larger than 1575.42 (L1).
Broadcast Correction
A predicted total UERE is provided in each satellite's Navigation message as the user range accuracy (URA), but it is minus ionospheric error. To help remove some of the effect of the ionospheric delay on the range derived from a single frequency receiver, there is an ionospheric correction available in another part of the Navigation message, subframe 4. However, this broadcast correction should not be expected to remove more than about three-quarters of the error, which is most pronounced on long baselines. Where the baselines between the receivers are short, the effect of the ionosphere can be small, but as the baseline grows, so does the significance of the ionospheric bias.
The Receiver Clock Bias, dT
The Receiver Clock Bias, dT
The third-largest error, which can be caused by the receiver clock, is its oscillator. Both a receiver’s measurement of phase differences and its generation of replica codes depend on the reliability of this internal frequency standard.
Typical Receiver Clocks
GPS receivers are usually equipped with quartz crystal clocks, which are relatively inexpensive and compact. They have low power requirements and long life spans. For these types of clocks, the frequency is generated by the piezoelectric effect in an oven-controlled quartz crystal disk, a device sometimes symbolized by OCXO. Their reliability ranges from a minimum of about 1 part in 108 to a maximum of about 1 part in 1010, a drift of about 0.1 nanoseconds in 1 second. Even at that, quartz clocks are not as stable as the atomic standards in the GPS satellites and are more sensitive to temperature changes, shock, and vibration. In other words, they're relatively stable, but they certainly aren't as sophisticated as those that are found in the GPS satellite. They're not atomic standards, nor need they be. Obviously, the receivers that we use would be tremendously expensive if the oscillators —if the clocks that were in them— had to be of that great stability. It really isn't necessary for a GPS receiver clock to be wonderful, because we are solving for time. There are four unknowns (x, y, z, and time) and, therefore, four observations to make the solution. Still, we can't get along without an oscillator in the receiver. It is necessary for producing the replica code, for example. The replica code needs to match the incoming signals from the satellites. So, obviously, a receiver clock is necessary, but it doesn't need to be anything like an atomic standard.
The Orbital Bias

Orbital bias has the potential to be the fourth-largest error. It is addressed in the broadcast ephemeris.
The orbital motion of GPS satellites is not only a result of the earth's gravitational attraction, there are several other forces that act on the satellite. The primary disturbing forces are the non-spherical nature of the earth's gravity (the earth is not equally dense in all its portions), tidal forces, the attractions of the sun and the moon, and solar radiation pressure as the satellite moves from darkness to light. All in all, it is a rather bumpy road for the satellite. The best model of these forces is the actual motion of the satellites themselves, and the government facilities distributed around the world, known collectively as the Control Segment or the Operational Control System (OCS), track them for that reason, among others. The modeling of the orbit by the Control Segment is good, but they can upload the ephemerides only so frequently. There is always a certain amount of age in the ephemerides and that means that the position of the satellite expressed in its ephemeris at the moment of observation cannot be perfect. So orbital bias could be thought of as the error in the broadcast ephemeris.
The Control Segment

The Control Segment
There are government tracking and uploading facilities distributed around the world. These facilities not only monitor the L-band signals from the GPS satellites and update their Navigation Messages, but also track the satellite’s health, their maneuvers, and many other things, even battery recharging. Taken together, these facilities are known as the Control Segment.
The Master Control Station (MCS), once located at Vandenberg Air Force Base in California, now resides at the Consolidated Space Operations Center (CSOC) at Schriever (formerly Falcon) Air Force Base near Colorado Springs, Colorado, and has been manned by the 2nd Space Operations Squadron (2SOPS), since 1992. There is an alternate MCS in at Vandenberg Tracking Station in California.
The 2SOPS squadron controls the satellites' orbits. For example, they maneuver the satellites from the highly eccentric orbits into which they are originally launched to the desired mission orbit and spacecraft orientation. They monitor the state of each satellite's onboard battery, solar, and propellant systems. They resolve satellite anomalies, activate spare satellites, and control Selective Availability (SA) and Anti-Spoofing (A/S). They dump the excess momentum from the wheels, the series of gyroscopic devices that stabilize each satellite. With the continuous constellation tracking data available and aided by Kalman filter estimation to manage the noise in the data, they calculate and update the parameters in the Navigation message (ephemeris, almanac, and clock corrections) to keep the information within limits, because the older it gets, the more its veracity deteriorates. This process is made possible by a persistent two-way communication with the constellation that includes both monitoring and uploading, accomplished through a network of ground antennas and monitoring stations.
The data that feeds the MCS comes from monitoring stations. These stations track the entire GPS constellation. In the past, there were limitations. There were only six tracking stations. It was possible for a satellite to go unmonitored for up to two hours each day. It was clear that the calculation of the ephemerides and the precise orbits of the constellation could be improved with more monitoring stations in a wider geographical distribution. It was also clear that if one of the six stations went down, the effectiveness of the Control Segment could be considerably hampered. These ideas, and others, led to a program of improvements known as the Legacy Accuracy Improvement Initiative, L-AII. During this initiative from August 18 to September 7 of 2005, six National Geospatial Intelligence Agency, NGA, stations were added to the Control Segment. This augmented the information forwarded to the MCS with data from Washington, D.C., England, Argentina, Ecuador, Bahrain, and Australia. With this 12-station network in place, every satellite in the GPS constellation was monitored almost continuously from at least three stations when it reached at least 5º above the horizon.
Today, there are 6 Air Force and the 11 National Geospatial-Intelligence Agency (NGA) monitoring stations. The monitoring stations track all the satellites; in fact, every GPS satellite is tracked by at least 3 of these stations all the time. The monitoring stations collect range measurements, atmospheric information, satellite's orbital information, clock errors, velocity, right ascension, and declination and send them to the MCS. They also provide pseudorange and carrier phase data to the MCS. The MCS needs this constant flow of information. It provides the basis for the computation of the almanacs, clock corrections, ephemerides, and other components that make up the Navigation message. The new stations also improve the geographical diversity of the Control Segment, and that helps with the MCS isolation of errors, for example, making the distinction between the effects of the clock error from ephemeris errors. In other words, the diagnosis and solution of problems in the system are more reliable now because the MCS has redundant observations of satellite anomalies with which to work. Testing has shown that the augmented Control Segment and subsequent improved modeling has improved the accuracy of clock corrections and ephemerides in the Navigation Message substantially, and may contribute to an increase in the accuracy of real-time GPS of 15% or more.
However, once the message is calculated, it needs to be sent back up to the satellites. Some of the stations have ground antennas for uploading. Four monitoring stations are collocated with such antennas. The stations at Ascension Island, Cape Canaveral, Diego Garcia, and Kwajalein upload navigation and program information to the satellites via S-band transmissions. The station at Cape Canaveral also has the capability to check satellites before launch.
The modernization of the Control Segment has been underway for some time, and it continues. In 2007, the Launch/Early Orbit, Anomaly Resolution, and Disposal Operations mission (LADO) PC-based ground system replaced the mainframe based Command-and-Control System (CCS). Since then, LADO has been upgraded several times. It uses Air Force Satellite Control Network (AFSCN) remote tracking stations only, not the dedicated GPS ground antennas to support the satellites from spacecraft separation through checkout, anomaly resolution, and all the way to end of life disposal. It also helps in the performance of satellite movements and the presentation of telemetry simulations to GPS payloads and subsystems. Air Force Space Command (AFSPC) accepted the LADO capability to handle the most modern GPS satellites at the time, the Block IIF. Another modernization program is known as the Next Generation Operational Control System or OCX. OCX will facilitate the full control of the new GPS signals like L5, as well as L2C, L1C, M code and the coming GPS III program.
The Tropospheric Effect, dtrop

Troposphere
The troposphere is that part of the atmosphere closest to the earth. It extends from the surface to about 9 km over the poles and about 16 km over the equator, but in this work, it will be combined with the tropopause and the stratosphere, as it is in much of GPS literature. Therefore, the following discussion of the tropospheric effect will include the layers of the earth’s atmosphere up to about 50 km above the surface. While the troposphere is no more cooperative than the ionosphere in terms of being consistent, the troposphere and the ionosphere are by no means alike in their effect on the satellite’s signal. The troposphere is refractive, its refraction of a GPS satellite’s signal is not related to its frequency. The refraction is tantamount to a delay in the arrival of a GPS satellite's signal. It can also be conceptualized as a distance added to the range the receiver measures between itself and the satellite. The troposphere is part of the electrically neutral layer of the earth’s atmosphere, meaning it is not ionized. The troposphere is also nondispersive for frequencies below 30 GHz or so. Therefore, L1, L2, and L5 are equally refracted. This means that the range between a receiver and a satellite will be shown to be a bit longer than it actually is. However, as it is in the ionosphere, density affects the severity of the delay of the GPS signal as it travels through the troposphere. For example, when a satellite is close to the horizon, the delay of the signal caused by the troposphere is maximized. The tropospheric delay of the signal from a satellite at zenith, directly above the receiver, is minimized.
Satellite elevation and tropospheric effect.
The situation is analogous to atmospheric refraction in astronomic observations; the effect increases as the energy passes through more of the atmosphere. The difference in GPS is that it is the delay, not the angular deviation caused by the changing density of the atmosphere, that is of primary interest. The GPS signal that travels the shortest path through the troposphere will be the least delayed by it. In other words, there is less tropospheric delay when the satellite is at the zenith of the receiver.
Modeling. Modeling the troposphere is one technique used to reduce the bias in GPS data processing, and it can be up to 95% effective. However, the residual 5% can be quite difficult to remove. Several a priori models have been developed, for example, the Saastamoinen model and the Hopfield models, which perform well when the satellites are at reasonably high elevation angles. However, it is advisable to limit GPS observations to those signals above 15% or so to ameliorate the effects of atmospheric delay.
The dry and wet components of refraction.
Refraction in the troposphere has a dry component and a wet component. The dry component which contributes most of the delay, perhaps 80% to 90%, is closely correlated to the atmospheric pressure. The dry component can be more easily estimated than the wet component. It is fortunate that the dry component contributes the larger portion of range error in the troposphere, because the size of the delay attributable to the wet component depends on the highly variable water vapor distribution in the atmosphere. Even though the wet component of the troposphere is nearer to the Earth’s surface, measurements of temperature and humidity are not strong indicators of conditions on the path between the receiver and the satellite. While instruments that can provide some idea of the conditions along the line between the satellite and the receiver are somewhat more helpful in modeling the tropospheric effect, the high cost of sending water vapor radiometers and radiosondes aloft generally restricts their use to only the most high-precision GPS work. In most cases, this aspect must remain in the purview of mathematical modeling; such calculations include a hydrostatic model with corrections and a horizontal gradient component. It is important to recognize that the index of tropospheric refraction decreases as height increases.
Atmosphere and Baseline Length

Receiver spacing and the atmospheric biases
There are other practical consequences of the atmospheric biases. As mentioned earlier, the character of the atmosphere is never homogeneous; therefore, the importance of atmospheric modeling increases as the distance between GPS receivers grows. Consider a signal traveling from one satellite to two receivers that are close together. That signal would be subjected to very similar atmospheric effects, and, therefore, atmospheric bias modeling would be less important to the accuracy of the measurement of the relative distance between them. But a signal traveling from the same satellite to two receivers that are far apart may pass through levels of atmosphere quite different from one another. In that case, atmospheric bias modeling would be more important. In other words, the importance of atmospheric correction increases as the differences in the atmosphere through which the GPS satellite signal must pass to reach the receivers increase. Such differences can generally be related to baseline length.
Multipath
Multipath, εmρ and εmφ

Multipath is an uncorrelated error. It is a range delay that has a different symbol in the two equations we talked about at the top. It is symbolized by εmρ in the pseudorange equation and εmφ in the carrier phase equation. As the name implies, it is the reception of the GPS signal via multiple paths rather than from a direct line of sight. It occurs when part of the signal from the satellite reaches the receiver after one or more reflections or scattering from the ground, a building, or another object. These reflected signals can interfere with the signal that reaches the receiver directly from the satellite and cause the correlation peak to become skewed. It is simple in principle. Since we are measuring distances to the satellites, and that is the foundation of the positions in GPS, a signal that bounces from an obstruction before it reaches the antenna of the GPS receiver causes a problem. If there's a bend in the signal, that upsets the distance, the range, that the receiver measures to the satellite. As illustrated here, the obstruction can be buildings, or really any reflective surface. The signal can reflect more than once. It can reflect from the ground. Multipath is one of the main reasons ground planes are used in geodetic work.
Since carrier phase multipath is based on a fraction of the carrier wavelength, and code multipath is relative to the chipping rate, the effect of multipath on pseudorange solutions is orders of magnitude larger than it is in carrier phase solutions. However, multipath in carrier phase is harder to mitigate than multipath in pseudoranges.
The high frequency of the GPS codes tends to limit the field over which multipath can contaminate pseudorange observations. Once a receiver has achieved lock, that is, its replica code is correlated with the incoming signal from the satellite, signals outside the expected chip length can be rejected. Generally speaking, multipath delays of less than one chip, those that are the result of a single reflection, are the most troublesome.
Fortunately, there are factors that distinguish reflected multipath signals from direct, line-of-sight, signals. For example, reflected signals at the frequencies used for L1, L2, and L5 tend to be weaker and more diffuse than the directly received signals. Another difference involves the circular polarization of the GPS signal. The polarization is actually reversed when the signal is reflected. Reflected, multipath signals become Left Hand Circular Polarized, LHCP, whereas the signals received directly from the GPS satellites are Right Hand Circular Polarized, RHCP. RHCP means that it rotates clockwise when observed in the direction of propagation. However, in the face of multiple reflections, the attribute is not determinative. In any case, these characteristics allow some multipath signals to be identified and rejected at the receiver’s antenna.
Antenna Design and Multipath
GPS antenna design can play a role in minimizing the effect of multipath. Ground planes, usually a metal sheet, are used with many antennas to reduce multipath interference by eliminating signals from low elevation angles. Generally, larger ground planes, multiple wavelengths in size, have a more stabilizing influence than smaller ground planes. However, such ground planes do not provide much protection from the propagation of waves along the ground plane itself. When a GPS signal’s wave front arrives at the edge of an antenna’s ground plane from below, it can induce a surface wave on the top of the plane that travels horizontally. Another way to mitigate this problem is the use of a choke ring antenna. Choke ring antennas, based on a design first introduced by the Jet Propulsion Laboratory (JPL), can reduce antenna gain at low elevations. This design contains a series of concentric circular troughs that are a bit more than a quarter of a wavelength deep. A choke ring antenna can prevent the formation of these surface waves. But neither ground planes nor choke rings remove the effect of reflected signals from above the antenna very effectively. There are signal processing techniques that can reduce multipath. A widely used strategy is the 15° cutoff or mask angle. This technique calls for tracking satellites only after they are more than 15° above the receiver’s horizon. Careful attention in placing the antenna away from reflective surfaces, such as nearby buildings, water, or vehicles, is another way to minimize the occurrence of multipath. The ground plane, seen on the right in the illustration, helps eliminate the bounce from the ground underneath the antenna. However, waves can almost crawl across the top of that ground plane and so there is the choke ring antenna, shown on the left in the illustration, can prevent these surface waves from propagating across the ground plane. I've mentioned the mask angle more than once. It is effective in ameliorating multipath. However, there really is no way to eliminate multipath entirely. It can be minimized by good location, away from reflective surfaces, and by uses of these sorts of antennas and also from software and the receiver itself. But, as far as I know, there is no way to absolutely eliminate the effect of multipath in all cases.
Receiver Noise
Receiver Noise, ερ and εφ
Receiver noise is directly related to thermal noise, dynamic stress, and so on in the GPS receiver itself. Receiver noise is also an uncorrelated error source, meaning the effects of both multipath and the receiver noise are not related to the length of the baseline between GPS receivers. They are uncorrelated in that regard. The effects of receiver noise on carrier phase measurements symbolized by εφ, like multipath, are small when compared to their effects on pseudorange measurements, ερ. Generally speaking, the receiver noise error is about 1% of the wavelength of the signal involved. In code solutions, the size of the error is related to chip width. For example, the receiver noise error in a C/A code solution might be about an order of magnitude more than it might be in a P(Y) code solution, and it would be even less in carrier phase solutions. Receiver noise is inevitable, and it must be considered, but it is a relatively small contributor to the GPS error budget, in most cases.
Differencing: Classification of GPS Positioning
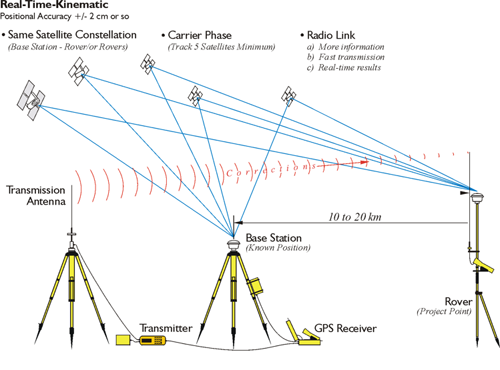
GPS work is sometimes divided into three categories; positioning, navigation, and timing (PNT). Most often, GPS surveying is concerned with the first of these, positioning. In general, there are two techniques used in surveying. They are kinematic and static. In static GPS surveying sessions, the receivers are motionless on the Earth during the observation. Because static work most often provides higher accuracy and more redundancy than kinematic work, it is usually done to establish control. The results of static GPS surveying are processed after the session is completed. In other words, the data is typically post-processed. The majority of GPS surveying control and geodetic work still relies on static applications.
In kinematic GPS surveying, the receivers are either in periodic or continuous motion. Kinematic GPS is done when real-time, or near real-time, results are needed. When the singular objective of kinematic work is positioning, the receivers move periodically using the start and stop methodology originated by Dr. Benjamin Remondi in the 1980s. When the receivers are in continuous motion, the objective may be acquisition of the location, attitude, and velocity of a moving platform (i.e., navigation), or positioning. The distinction between navigation and positioning is lessening.
Kinematic applications imply movement, one or more GPS receivers actually in motion during their observations. A moving GPS receiver on land, sea, or air is characteristic of kinematic GPS. Other characteristics of the application include results in real time and little redundancy. Hydrography, aerial mapping, gravimetric, and more and more land surveying projects are done using kinematic GPS.
Relative positioning is different than autonomous positioning. An independent receiver, an autonomous receiver, must rely on the information in the Navigation Message. In that sort of configuration, it has no way to improve on the corrections. In relative (aka differential) positioning, there are two receivers; one on a known point whose coordinates are well-established, and a second receiver on an unknown point. With this arrangement, the new unknown position can be established relative to the known point. Relative (differential) positioning creates solutions that are positionally superior to autonomous positioning, in large part because it is possible to improve on the corrections available in the Navigation Message.

The term differential GPS, or DGPS, has come into common usage as well. Use of this acronym usually indicates a method of relative positioning where usually coded pseudorange measurements are used rather than carrier phase, though it is sometimes used in context of carrier phase solutions.
The Navigation Solution

Another type of point positioning is known as absolute positioning, single-point positioning, or the Navigation solution. It is characterized by a single receiver measuring its range to a minimum of four satellites simultaneously. An autonomous GPS positioning is not post-processed, and there is really no communication with a station that's on a known point. In other words, autonomous positioning is not differential (relative); the receiver is operating independently. As always, four satellites are required, as indicated here. The receiver is on an unknown position and must solve for its own receiver clock error. It needs to solve for x, y, z, and time. The Navigation solution is, in one sense, the fulfillment of the original idea behind GPS. It relies on a coded pseudorange measurement and can be used for virtually instantaneous positioning. In this method, the positions of the satellites are available from the data in their broadcast ephemerides. The satellite clock offset, and the ionospheric correction are also available from the Navigation messages of all four satellites. As you know, these corrections from that message are not ideal. Even if all the data in the navigation message contained no errors, and they surely do, four unknowns remain: the position of the receiver in three Cartesian coordinates, ux , uy , and uz , and the receiver’s clock error dTu . Three pseudoranges provide enough data to solve for ux , uy , and uz . And the fourth pseudorange provides the information for the solution of the receiver’s clock offset. The ability to measure dT, the receiver’s clock error, is one reason the moderate stability of quartz crystal clock technology is entirely adequate as a receiver oscillator. A unique solution is found here because the number of unknowns is not greater than the number of observations. The receiver tracks a minimum of 4 satellites simultaneously; therefore, these four equations can be solved simultaneously for every epoch of the observation. An epoch in GPS is a very short period of observation time (i.e. 1 second or perhaps less), and is generally just a small part of a longer measurement. However, theoretically, there is enough information in any single epoch to solve these equations. This is the reason the trajectory of a receiver in a moving vehicle can be determined by this method. With 4 satellites available, resolution of a receiver’s position and velocity are both available through the simultaneous solution of these four equations.
Relative Positioning
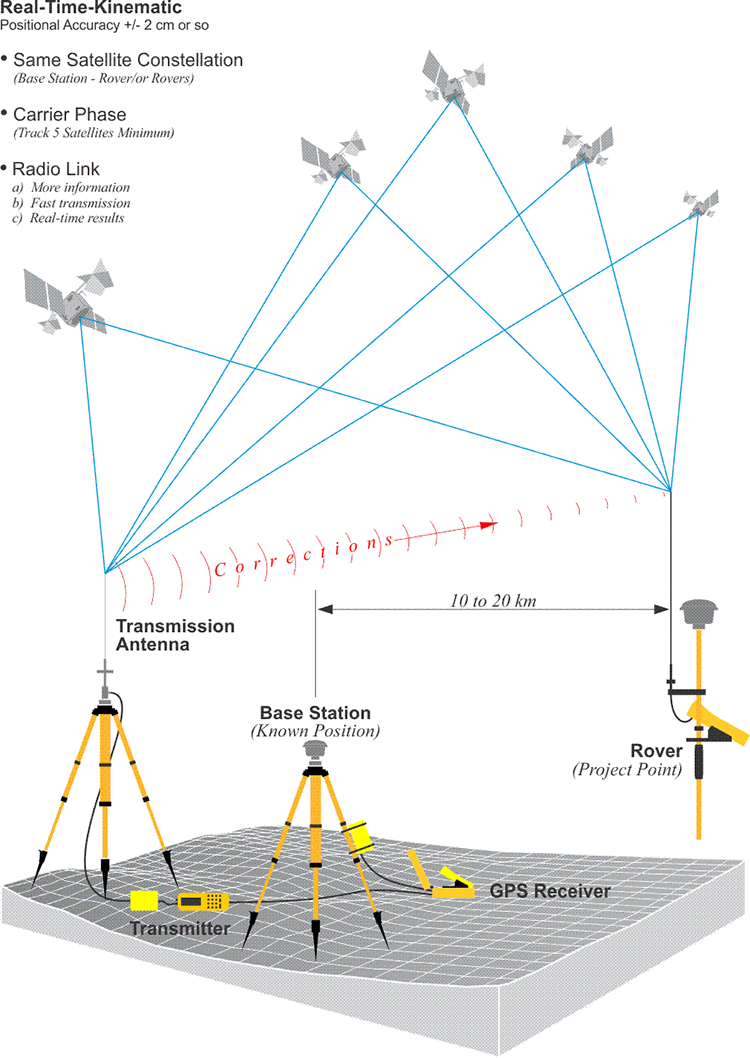
One receiver is employed in single point positioning. A minimum of two receivers are involved in relative or differential positioning. The term differential GPS, or DGPS, sometimes indicates the application of this technique with coded pseudorange measurements, whereas relative GPS usually indicates the application of this technique with carrier phase measurements. However, these definitions are by no means universal, and the use of the terms relative and differential GPS have become virtually interchangeable.
In relative positioning, one of the two receivers involved occupies a known position during the session. It is the base. The objective of the work is the determination of the position of the other, the rover, relative to the base. Both receivers observe the same constellation of satellites at the same time, and because, in typical applications, the vector between the base and the rover, known as a baseline, is so short compared with the 20,000-km altitude of the GPS satellites, there is extensive correlation between observations at the base and the rover. In other words, the two receivers record very similar errors (biases), and since the base’s position is known, corrections can be generated there that can be used to improve the solution at the rover.
If the carrier phase observable is used in relative positioning, baseline measurement accuracies of ± (1 cm + 2 ppm) are achievable. It is possible for GPS measurements of baselines to be as accurate as 1 ppm or even 0.1 ppm. If realized, that would mean that the measurement of a nine-mile baseline would approach its actual length within ±0.05 ft. (1 ppm) or ±0.005 ft. (0.1 ppm).

The autonomous solution can be contrasted with relative positioning or differencing. In this image, you see a GPS receiver working at the same time as a continuously operating reference station that is on a known point. Both are collecting the same constellation of six satellites. And the CORS station (Continuously Operating Reference Station), downloads its observations to an archive. This is a base station archive that, in fact, can be made available on the Internet, as the National Geodetic Survey does. The GPS receiver can download its data at an unknown point to its memory. Post-mission, the two data sets can be brought together and post-processed on a computer. The corrections can be derived from the fact that the Continuously Operating Reference Station knows where it is. This allows the solution at the GPS receiver at the unknown point to be corrected to its actual position relative to the CORS. This is relative positioning. The vector between such a pair of receivers is known as a baseline. It's the simultaneity —in other words, the fact that they're observing the same constellation at the same time— that makes it possible to do accurate GPS in this way.
Networks

Network and multireceiver positioning are obvious extensions of relative positioning. Both the creation of a closed network of points by combining individually observed baselines and the operation of three or more receivers simultaneously have advantages. For example, the baselines have redundant measurements and similar, if not identical, range errors (biases). The processing methods in such an arrangement can nearly eliminate many of the biases introduced by imperfect clocks and the atmosphere. These processing strategies are based on computing the differences between simultaneous GPS carrier phase observations.
Differencing

Please recall that the biases in both the pseudorange and the carrier phase equations discussed at the top obscure the true geometric ranges between the receivers to the satellites, which then contaminate the measurement of the baseline between the receivers. In other words, to reveal the actual vectors between two or more receivers used in relative positioning, those errors must be diminished to the degree that is possible. Fortunately, some of those embedded biases can be virtually eliminated by combining the simultaneous observables from the receivers in processes known as differencing. Even though the noise is increased by a factor of two with each differencing operation, it is typically used in commercial data processing software for both pseudorange and carrier phase measurements. There are three types of differencing, the single difference, double difference, and triple difference. Within the single difference category, there are the between-receivers single difference and the between-satellites single difference. Both require that all the receivers observed the same satellites at the same time. In GPS, the word differencing has come to represent several types of simultaneous baseline solutions of combined measurements. One of the foundations of differencing is the idea of the baseline as it is used in GPS. For example, a single difference, also known as a between-receivers difference, can refer to the difference in the simultaneous carrier phase measurements from one GPS satellite as measured by two different receivers. In the illustration, there are two receivers —q and r— observing the same satellite.
Between-Receivers Single Difference
A between-receivers single difference reduces the effect of biases, even though it doesn’t eliminate them. Since the two receivers are both observing the same satellite at the same time, the difference between the satellite clock bias, dt, at the first receiver and dt at the second receiver, Δdt, is obviously zero. Also, since the baseline is typically short compared with the 20,000-km altitude of the GPS satellites, the atmospheric biases and the orbital errors, i.e., ephemeris errors, recorded by the two receivers at each end are similar. This correlation obviously decreases as the length of the baseline increases. Generally speaking, this correlation allows centimeter level carrier phase positioning with baselines up to 10 km or so, and meter level positioning with baselines of a few hundreds of kilometers using pseudorange observations.
The between-receivers single difference provides better position estimates for the receivers by subtracting, differencing, each receiver’s observation equation from the other. For example, if one of the receivers is a base standing at a control station whose position is known, it follows that the size of the positional error of the receiver there is knowable. Therefore, the positional error at the other end of the baseline can be estimated by finding the difference between the biases at the base and the biases at the rover. Corrections can then be generated which can reduce the three-dimensional positional error at the unknown point by reducing the level of the biases there. It is primarily this correlation and the subsequent ability to reduce the level of error that distinguishes differenced relative positioning from single point positioning.

The between-satellites single difference involves a single receiver observing two GPS satellites simultaneously and the code and/or phase measurement of one satellite are differenced, subtracted, from the other. The data available from the between-satellites difference allows the elimination of the receiver clock error because there is only one involved. And the atmospheric effects on the two satellite signals are again nearly identical as they come into the lone receiver, so the effects of the ionospheric and tropospheric delays are reduced. However, unlike the between-receivers single difference, the between-satellites single difference does not provide a better position estimate for the receiver involved. In fact, the resulting position of the receiver is not better than would be derived from single point positioning.

When the two types of single differences are combined, the result is known as a double difference. A double difference can be said to be a between-satellite single difference of a between-receiver single difference. The improved positions from the between-receiver single difference step are not further enhanced by the combination with the between-satellite single difference. Still, including the between-satellite single difference is useful because the combination virtually eliminates clock errors, both the satellite and receiver clock errors. The removal of the receiver clock bias in the double difference makes it possible to segregate the errors attributable to the receiver clock biases from those from other sources. This segregation improves the efficiency of the estimation of the integer cycle ambiguity in a carrier phase observation, N. In other words, the reduction of all the non-integer biases makes the computation of the final accurate positions more efficient.
The double difference, for all practical purposes, has eliminated the receiver clock errors and the satellite clock errors. This is used in most GPS post-processing and software. The integer ambiguity, N, still remains with the carrier phase observation.

A triple difference is the difference of two double differences over two different epochs. The triple difference has other names. It is also known as the receiver satellite-time triple difference and the between-epochs difference. Triple differencing serves as a good pre-processing step, because it can be used to detect and repair cycle slips.
Cycle Slip

Here's a graphic to give the idea of a cycle slip. As you see here, the cycle slip is indicated in a double difference, here, as a jump from one place to another. And in a triple difference, it's a spike.
A cycle slip is a discontinuity in a receiver’s phase lock on a satellite’s signal. A power loss, a very low signal-to-noise ratio, a failure of the receiver software, a malfunctioning satellite oscillator can cause a cycle slip. It can also be caused by severe ionospheric conditions. Most common, however, are obstructions such as buildings, trees, etc., that are so solid they prevent the satellite signal from being tracked by the receiver. Under such circumstances, when the satellite reappears, the tracking resumes.
Coded pseudorange measurements are not as affected by cycle slips as are carrier phase measurements. On the other hand, carrier phase positioning accuracy suffers if cycle slips are not detected and repaired. A cycle slip causes the critical component for successful carrier phase positioning, a resolved integer cycle ambiguity, N, to become instantly unknown again. In other words, lock is lost. When that happens, correct positioning requires that N be reestablished.
There are several methods of handling cycle slips. They are often controlled in post-processing rather than real-time.
Repairing Cycle Slips
In post-processing, the location and their size of cycle slips must be determined; then the data set can be repaired with the application of a fixed quantity to all the subsequent phase observations. One approach is to hold the initial positions of the stations occupied by the receivers as fixed, and edit the data manually. This has proven to work, but would does try patience. Another approach is to model the data on a satellite-dependent basis with continuous polynomials to find the breaks and then manually edit the data set a few cycles at a time. In fact, several methods are available to find the lost integer phase value, but they all involve testing quantities.
One of the most convenient of these methods is based on the triple difference. It can provide an automated cycle slip detection system that is not confused by clock drift and, once least-squares convergence has been achieved, it can provide initial station positions even using the unrepaired phase combinations. They may still contain cycle slips, but the data can nevertheless be used to process approximate baseline vectors. Then the residuals of these solutions are tested, sometimes through several iterations. Proceeding from its own station solutions, the triple difference can predict how many cycles will occur over a particular time interval. Therefore, by evaluating triple difference residuals over that particular interval, it is not only possible to determine which satellites have integer jumps, but also the number of cycles that have actually been lost. In a sound triple difference solution without cycle slips, the residuals are usually limited to fractions of a cycle. Only those containing cycle slips have residuals close to one cycle or larger. Once cycle slips are discovered, their correction can be systematic.
For example, suppose the residuals of one component double difference of a triple-difference solution revealed that the residual of satellite PRN 16 minus the residual of satellite PRN 17 was 8.96 cycles. Further, suppose that the residuals from the second component double difference showed that the residual of satellite PRN 17 minus the residual of satellite PRN 20 was 14.04 cycles. Then, one might remove 9 cycles from PRN 16 and 14 cycles from PRN 20 for all the subsequent epochs of the observation. However, the process might result in a common integer error for PRNS 16, 17, and 20. Still, small jumps of a couple of cycles can be detected and fixed in the double-difference solutions. In other words, before attempting double difference solutions, the observations should be corrected for cycle slips identified from the triple difference solution. And even though small jumps undiscovered in the triple difference solution might remain in the data sets, the double difference residuals will reveal them at the epoch where they occurred. However, some conditions may prevent the resolution of cycle slips down to the one-cycle level. Inaccurate satellite ephemerides, noisy data, errors in the receiver’s initial positions, or severe ionospheric effects all can limit the effectiveness of cycle-slip fixing. In difficult cases, a detailed inspection of the residuals might be the best way to locate the problem.
Components of the Carrier Phase Observable

Components of the carrier phase observable
From the moment a receiver locks onto a satellite to the end of the observation, the carrier phase observable can be divided into three parts. Two of them do not change during the session, and one of them does change. The fractional initial phase is established at the first instant of the lock-on. When the receiver starts tracking the satellite, it is highly unlikely to acquire the satellite’s signal precisely at the beginning of a wavelength's phase cycle. It will grab on at some fractional part of a phase, and this fractional phase will remain unchanged for the duration of the observation. It is called the fractional initial phase or the phase measurement and is symbolized in the equation above by . The integer cycle ambiguity N represents the number of full phase cycles between the receiver and the satellite at the first instant of the receiver’s lock-on. It can also be labeled the carrier phase ambiguity or the cycle count at lock-on. It does not change from the moment of the lock to the end of the observation, unless that lock is lost. But when there is a cycle slip, lock is lost, and by the time the receiver reacquires the signal, the normally constant integer ambiguity has changed. In that case, the receiver loses its place in its count of the integer number of cycles is lost. The value ß is the count of the number of full phase cycles coming in throughout the observation. Of course, the count grows from the moment of lock on until the end of the observation. In other words, ß is the receiver’s record of the consecutive change in full phase cycles, 1, 2, 3, 4 . . ., between the receiver and the satellite as the satellite flies over. If the observation proceeds without cycle slips, the observed cycle count is the only one of three numbers that changes.
You may remember from the first lesson that when a GPS receiver locks onto a signal from a satellite, it can acquire the fractional initial phase, α. It can interpret that fractional initial phase by comparing what's coming in from the satellite with the replica frequency that it has on-board in its circuits. That comparison can take place pretty quickly, and it doesn't need to change through the observation of that satellite by that receiver. You may also remember that in an EDM measurement, since it is two-way, the EDM can send out frequencies of different lengths to resolve the cycle ambiguity. GPS doesn't have that advantage. It's a one-way system with set carrier wavelengths, so N is somewhat elusive. As the satellite moves along its orbit, the GPS receiver does observed cycle count. In other words, it can count the number of full wavelengths, ß, since its lock-on, and how much they have changed as the satellite moves from one place to another in its orbit. Armed with an initial pseudorange solution, the receiver can estimate the integer ambiguity (carrier phase ambiguity), N. The initial pseudorange observation gives the receiver an idea how many full cycles there are in that N value. From that starting place, it can use a double difference to nail down that carrier phased ambiguity. Perhaps you have heard the fixed solution terminology in post-processing software in GPS. It is often mentioned as opposed to a float solution. A fixed solution means that the integers are fixed. The N has been solved. A fixed solution is superior to a float solution.
Just to reiterate this— the first fractional initial phase occurs at the first instant of lock-on. The receiver starts tracking the incoming phase from the satellite. It can't yet know how to achieve the perfect synchronization. Lacking this knowledge, the receiver grabs on to the satellite's incoming signal at some fractional part. This fractional part does not change for the duration of the observation. The integer number of cycles (the carrier phase ambiguity) is the integer number of cycles of phase that are present at the moment of lock-on. The observed cycle count is the receiver's consecutive counting of the change in full phase cycles between the receiver and the satellite as the satellite flies over. Of these three terms, ß is the only number that changes. That is, if the observation proceeds correctly. In other words, without any cycle slips. In the carrier phase observation, there are two values that do not change: the fractional initial phase and the integer cycle ambiguity, N. Only the cycle count changes, unless, of course, there's a cycle slip. When lock is lost, a cycle slip occurs. It can be a power loss, an obstruction, low signal to noise ratio (SNR), anything that breaks the signal from the satellite to the receiver. When there is a cycle slip, the receiver loses its place and its count of the number of cycles, the integer lock is also lost, and re-initialization is necessary.
Fixing Cycle Slips

In carrier phase post-processing, the first solution is typically a simple pseudorange single point position at each end of the baseline. These code solutions provide the approximate position of each of the two receiver’s antennas. Each position establishes a search area, a three-dimensional volume of uncertainty, the size of which is defined by the accuracy of the code solution. The correct position of the receiver is contained within it somewhere. The computational time required to find it depends on the size of the search area. Next, cycle slips are addressed because the subsequent instantaneous phase jumps will defeat the upcoming double differencing. Triple differencing is not as affected by cycle slips and is insensitive to integer ambiguities, so it typically precedes double differencing and is used to clean the data by detecting and repairing cycle slips. In fact, pre-processing using the triple difference to weed out and fix cycle slips is one of its primary appeals. As to detection, when a large residual appears in one of the triple difference’s component double differences, it is likely caused by a cycle slip, so the satellite pairs can be sorted until the offending signal is singled-out and repaired. Triple differencing can also provide first positions for the receivers. While the receiver coordinates that result are usually more accurate than pseudorange solutions, their geometric strength is weak and not sufficiently accurate for determining short baselines. Nevertheless, they provide a starting point for the more accurate double-difference solutions that follow.
Discussion
Discussion Instructions
To continue the discussion begun by this lesson, I would like to pose this question:
Consider the effect of biases in the GPS error budget on the measurement of the length of a baseline between two GPS receivers. What differences can you think of between their effect on the measurement of a long baseline as opposed to a short one?
To participate in the discussion, please go to the Lesson 2 Discussion Forum in Canvas. (That forum can be accessed at any time by going to the GEOG 862 course in Canvas and then looking inside the Lesson 2 module.)
Summary
Differencing is an ingenious approach to minimizing the effect of biases in both pseudorange and carrier phase measurements. It is a technique that largely overcomes the impossibility of perfect time synchronization. Double differencing is the most widely used formulation. Double differencing still contains the initial integer ambiguities, of course. And the estimates of the ambiguities generated by the initial processing are usually not integers; in other words, some orbital errors and atmospheric errors remain. But with the knowledge that the ambiguities ought to be integers, during subsequent processing, it is possible to force estimates for the ambiguities that are, in fact, integers. When the integers are so fixed, the results are known as a fixed solution, rather than a float solution. It is the double differenced carrier phase based fixed solution that makes the very high accuracy possible with GPS.
However, it is important to remember that multipath, cycle slips, incorrect instrument heights, and a score of other errors whose effects can be minimized or eliminated by good practice are simply not within the purview of differencing at all. The unavoidable biases that can be managed by differencing— including clock, atmospheric, and orbital errors—can have their effects drastically reduced by the proper selection of baselines, the optimal length of the observation sessions, and several other considerations included in the design of a GPS survey. But such decisions require an understanding of the sources of these biases and the conditions that govern their magnitudes. The adage of, “garbage in, garbage out,” is as true of GPS as any other surveying procedure. The management of errors cannot be relegated to mathematics alone.
Before you go on to Lesson 3, double-check the Lesson 2 Checklist to make sure you have completed all of the activities listed there.



