MATLAB is essentially vector-based, so much data that will be manipulated is commonly structured in the form of arrays of values (vectors and matrices). If you don't commonly use other programming languages, then think of arrays as the grid of values in a spreadsheet program. Mathematical operations are designed to be carried out on arrays. In this lesson we'll go through a variety of methods to create and interact with arrays.

Learning Outcomes

By the end of this lesson, you should be able to:

• Use a variety of methods to construct arrays
• Query the attributes of an array
• Perform simple mathematical calculations with arrays
• Make a simple plot on two-dimensional axes

Lesson Roadmap

To Read	Lesson 2 (this web site)	here
To Do	Lesson 2 Quiz Problem Set 1	Canvas Canvas

Questions?

If you have questions, please feel free to post them to the Questions? Discussion forum in Canvas. I will check that forum daily. While you are there, feel free to post your own responses if you, too, are able to help a classmate.

Make a 1D vector and query its attributes

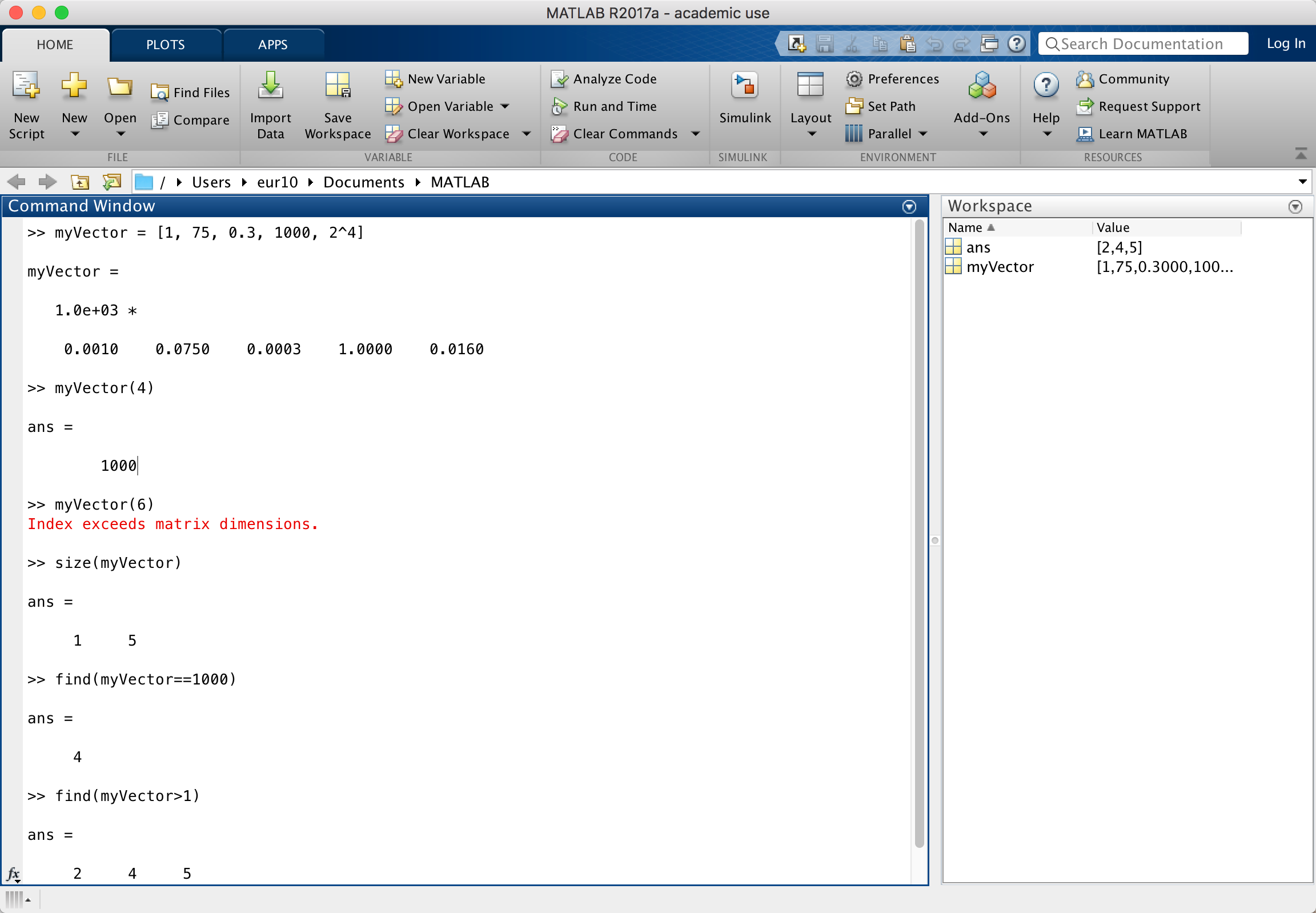
You can create a row vector by naming each of its elements explicitly. Put them inside square brackets with commas or spaces separating elements. For example, I'm going to create a row vector and name it myVector. It's going to have 5 numbers in it.

>> myVector = [1, 75, 0.3, 1000, 2^4]

myVector =

   1.0e+03 * 
    0.0010    0.0750    0.0003    1.0000    0.0160

Okay, that's fine. Let's say I already forgot what the fourth number in myVector is. Find out by asking MATLAB. Use parentheses to specify that you want to know the value of the 4th entry:

>> myVector(4)

ans =

        1000

MATLAB will give you an error message if you try to ask it for a value that doesn't exist:

>> myVector(6)
	Index exceeds matrix dimensions.

In the example above, myVector only has 5 numbers in it, so asking for the value of the sixth number doesn't make sense. The command size is useful for reminding yourself about the dimensions of a vector or matrix. When you ask MATLAB for the size of a vector or matrix it returns a vector with two entries: the number of rows and the number of columns.

>> size(myVector)

ans =

     1     5

Logical operators

The command find is good if you want to search for specific entries:

>> find(myVector==1000)

ans =

     4
>> find(myVector>1)

ans =

     2     4     5

In the above examples using find, MATLAB returns the indices (positions) of the values of the vector that match what you were looking for, not the values themselves. When I wrote find(myVector==1000) I was asking MATLAB which number in myVector is equal to 1000. MATLAB answered that it was the 4th entry. When I wrote find(myVector>1) I was asking MATLAB which numbers in myVector have values greater than 1. MATLAB answered that the 2nd, 4th, and 5th entries are greater than 1.

Arithmetic with vectors

Any arithmetic you perform on a vector with a scalar is by default performed piecewise on each vector element. For the following examples, I'm going to create a vector x and use it to demonstrate what I mean. You should open up MATLAB and follow along to verify my examples for yourself. First let's create x and then multiply it by 2.

>> x=[1 3 5 9 15];
>> x*2

ans =

     2     6    10    18    30

>> x

x =

     1     3     5     9    15

What is the most important thing to notice about this sequence of commands? The actual value of x didn't change even though we multiplied it by 2. Huh! Is that counterintuitive? Maybe. Think of it this way. You asked MATLAB what the answer would be if you multiplied x by 2 and it told you. If you actually want to set x equal to a new value you have to use = for assignment, like so:

>> x=[1 3 5 9 15];

>> x=x*2

x =

     2     6    10    18    30

Now you have overwritten the original value of x. Maybe you want to keep the old value of x. That's fine. Just assign a new variable to the product of x and 2, like so:

>> x=[1 3 5 9 15];

>> doubleX=x*2

doubleX =

     2     6    10    18    30

>> x

x =

     1     3     5     9    15

Addition, subtraction and division all work the same way as multiplication. I'm going to repeat what I said before because it will be important later: These element-by-element operations work like they do because in our examples, we have a one-dimensional vector, x,  and a scalar. Arrays and array operations (when x has more dimensions or there isn't a scalar) will be discussed later.

Standard simple statistical calculations such as mean, median, mode, and sum are all performed over the entire vector x unless you tell MATLAB to use a subset of the vector. Use the : to specify a range within a vector.

>> x=[1 3 5 9 15];

>> x(1:3)

ans =

     1     3     5

>> mean(x(3:5))

ans =

    9.6667

In the snippet above I asked MATLAB for the first three elements of x. Then I asked MATLAB to take the mean of the 3rd through 5th elements in x.

Check yourself!

Make a column vector

A column vector is created inside square brackets with semicolons or returns separating elements. You can turn a row vector into a column vector (or the other way around) with the transpose operator, which is a single quote mark '.

>> x=[2 4 6 8 10];
>> y=[1;3;5;7;9];
>> x

x =

     2     4     6     8    10

>> y

y =

     1
     3
     5
     7
     9

Vector arithmetic

Who cares whether a vector is a row vector or a column vector, you say? Well, if all of your vectors are of the same type and the same length then adding one to the other and subtracting one from the other of them works piece by piece:

>> x+x

ans =

     4     8    12    16    20

>> y+y

ans =

     2
     6
    10
    14
    18

But adding and subtracting when one vector is a row vector and the other one is a column vector doesn't work piece by piece:

>> M=x+y

M =

     3     5     7     9    11
     5     7     9    11    13
     7     9    11    13    15
     9    11    13    15    17
    11    13    15    17    19

What did MATLAB do here? It constructed a 5x5 matrix M in the following way. The first row of M is x(1)+y(1), x(2)+y(1), x(3)+y(1), x(4)+y(1), x(5)+y(1). The second row of M is x(1)+y(2), x(2)+y(2), x(3)+y(2), x(4)+y(2), x(5)+y(2). And so forth. The number of columns of one vector have to equal the number of rows of the other vector for this to work.

Dot products and cross products

You can also multiply and divide two vectors piece by piece, but you have to tell MATLAB you want to do it that way by using the dot product .*:

>> x.*x

ans =

     4    16    36    64   100

>> y.*y

ans =

     1
     9
    25
    49
    81

You'll get an error message if you try to multiply x by x by merely writing x*x. However, you can multiply x by y by just typing x*y since one of them is a column vector and the other is a row vector and the number of columns of x equals the number of rows in y. Try it! You get

>> x*y

ans =

   190

Why? Because you are basically asking MATLAB to take the cross product of two orthogonal vectors, so the answer is a scalar. The actual calculation is equivalent to:

>> x(1)*y(1)+x(2)*y(2)+x(3)*y(3)+x(4)*y(4)+x(5)*y(5)

ans =

   190

Check yourself!

Doing it by hand is okay . . . once

Up until now we created vectors by entering each element of the vector by hand. This was okay at the time because all of our vectors were small. Most Earth science datasets and model runs, on the other hand, are large and have a lot of datapoints, and there's no way you want to be typing in values by hand. Commonly, you want a regularly spaced array in which you specify the increment or else you specify the number of data points you want and let MATLAB set the increment.

Create a vector with constant spacing

Way 1:  specify the spacing

To create a vector with spacing specified you can use the : operator and type beginningNumber : increment : endNumber. The default if you don’t specify an increment is to increment by 1. You can also use fractional numbers and negative numbers with this technique.

Way 2: specify the number of elements

Another way to create a vector with constant spacing is to use linspace and set the vector with linspace(beginningNumber , endNumber, numberOfElements). If you don’t specify the number of elements, the default is 100. MATLAB will figure out the spacing for you.

You can also create vectors with regular logarithmic spacing instead of linear spacing. In this case you use logspace and type logspace(beginningExponent, endExponent, numberOfElements). The default here is 100 elements as well.

Let's say I want to make a vector that goes from 10 to 20 by ones. We know several ways to do this by now. Here are a few:

>> x=10:1:20 
  x =     10    11    12    13    14    15    16    17    18    19    20
 
>> x=10:20 
  x =     10    11    12    13    14    15    16    17    18    19    20
 
>> x=linspace(10,20,11) 
  x =     10    11    12    13    14    15    16    17    18    19    20
 
>> x=(0:10)+10 
  x =     10    11    12    13    14    15    16    17    18    19    20
 
>> a=10:15; 
>> b=16:20; 
>> x=[a b] 
  x =     10    11    12    13    14    15    16    17    18    19    20

There's lots of ways to skin this cat.

2-D matrix creation

A 2-D matrix is created inside of square brackets with spaces or commas between elements in a row and semicolons or returns separating rows. Rows have to have the same number of elements. You can use multiple linspace or : inside the square brackets, too.

Special matrices

Special matrices include zeros(numberOfRows, numberOfColumns), ones(numberOfRows, numberOfColumns), and eye(number). The identity matrix eye, in which ones appear along the diagonal but all other elements equal zero, is always square so you just specify one number for the dimension.

>> zeros(2,3)
ans =
     0     0     0
     0     0     0
>> ones(5,2)
ans =
     1     1
     1     1
     1     1
     1     1
     1     1
>> eye(6)
ans =
     1     0     0     0     0     0
     0     1     0     0     0     0
     0     0     1     0     0     0
     0     0     0     1     0     0
     0     0     0     0     1     0
     0     0     0     0     0     1

We've already practiced using parentheses to address a certain element of a vector. You can also use that technique to address a specific spot in a matrix. For example, v(1) addresses the first element in a vector v. M(1,1) addresses the element in the top left corner of the matrix M. In the example below I make a 3x3 matrix M. Then I ask it for the element in the second row and third column. It's just like playing Battleship except both the columns and rows are designated by numbers.

>> M=[1 2 3; 4 5 6; 7 8 9];
M =
     1     2     3

     4     5     6

     7     8     9

>> M(2,3) 
ans = 
     6

Use the colon operator to address a range of elements in a vector or matrix. For example, v(:) addresses all the elements of a vector, v(a:b) addresses elements a through b in vector v. M(:,a) addresses column a, M(a,:) addresses row a, M(:,a:b) addresses columns a through b, M(a:b,:) addresses rows a through b, M(a:b,c:d) addresses the intersection of rows a through b and columns c through d.

>> M(:,2)
ans =
     2

     5

     8
>> M(3,:) 
ans = 
     7     8     9 
>> M(1:2,2:3) 
ans = 
     2     3

     5     6

Use a square bracket to address nonconsecutive elements in a vector or matrix. For example v([a,b,c:d]) addresses elements a, b, and c through d. M([a,b],[c:d,e]) addresses the intersection of rows a and b and columns c through d and e.

>> M([1,3],1:3)
ans =
     1     2     3

     7     8     9

Other games you can play

To append an element to a vector just specify a value at the desired position. If it is not the next consecutive position, MATLAB pads the elements in between with zeros. You can append existing vectors to each other if they are all row vectors or all column vectors.

>> v=1:20;
>> v(25)=7.6
v =
  Columns 1 through 9
    1.0000    2.0000    3.0000    4.0000    5.0000    6.0000    7.0000    8.0000    9.0000
  Columns 10 through 18
   10.0000   11.0000   12.0000   13.0000   14.0000   15.0000   16.0000   17.0000   18.0000
  Columns 19 through 25
   19.0000   20.0000         0         0         0         0    7.6000

To append vectors to a matrix you need to make sure the dimensions work out so that all rows have the same number of elements.

Use empty brackets to delete an element from a vector or a row/column from a matrix. Deleting is not the same as assigning zero to the value of that element. Using empty brackets to delete elements from a matrix works if you are going to delete a whole row or a whole column, but not just one element. See in the snippet below a successful deletion of the fourth element of a vector, and what happens when I try to delete just one element from a 4x3 matrix.

>> v=[1:5];
>> v(4)=[]
v =
     1     2     3     5
>> M=ones(4,3);
>> M(1,1)=[]
A null assignment can have only one non-colon index.

diag on a vector creates a matrix whose diagonal is the initial vector and whose other elements are zero. With a matrix, diag pulls out the diagonal elements and makes a vector out of them.

>> v=1:5
v =
     1     2     3     4     5
>> diag(v)
ans =
     1     0     0     0     0
     0     2     0     0     0
     0     0     3     0     0
     0     0     0     4     0
     0     0     0     0     5
>> diag(ans)
ans =
     1
     2
     3
     4
     5

reshape has syntax reshape(M,a,b). It takes a matrix M that used to have x rows and y columns and turns it into a matrix with a rows and b columns. a*b must equal x*y for this to work.

plot(x,y) creates a figure window and plots the values of vector x on the x axis versus the values of vector y on the y axis. MATLAB defaults to a blue solid line connecting all the data points, but you can specify a range of linestyles, colors, and symbols. The vectors x and y need to be the same length.

If you want more than one dataset on the same axes, there are a few ways to do it. You can specify several pairs of vectors in the same plot command, you can type hold on in between plot commands, or you can use the line command for all subsequent plots after the first plot command. Note that line only takes two arguments (x and y values), so you can't use it if you want to plot discrete data points.

MATLAB defaults to adapting the axes ranges to the range of values in the vectors being plotted. To set specific axes ranges instead, use axis([xMin,xMax,yMin,yMax])

>> x=linspace(1,10);
>> y=randn(size(x));
>> z=y*.5;
>> plot(x,y,'r-','linewidth',2);
>> hold on;
>> plot(x,y,'ko','markerfacecolor','c');
>> line(x,z);

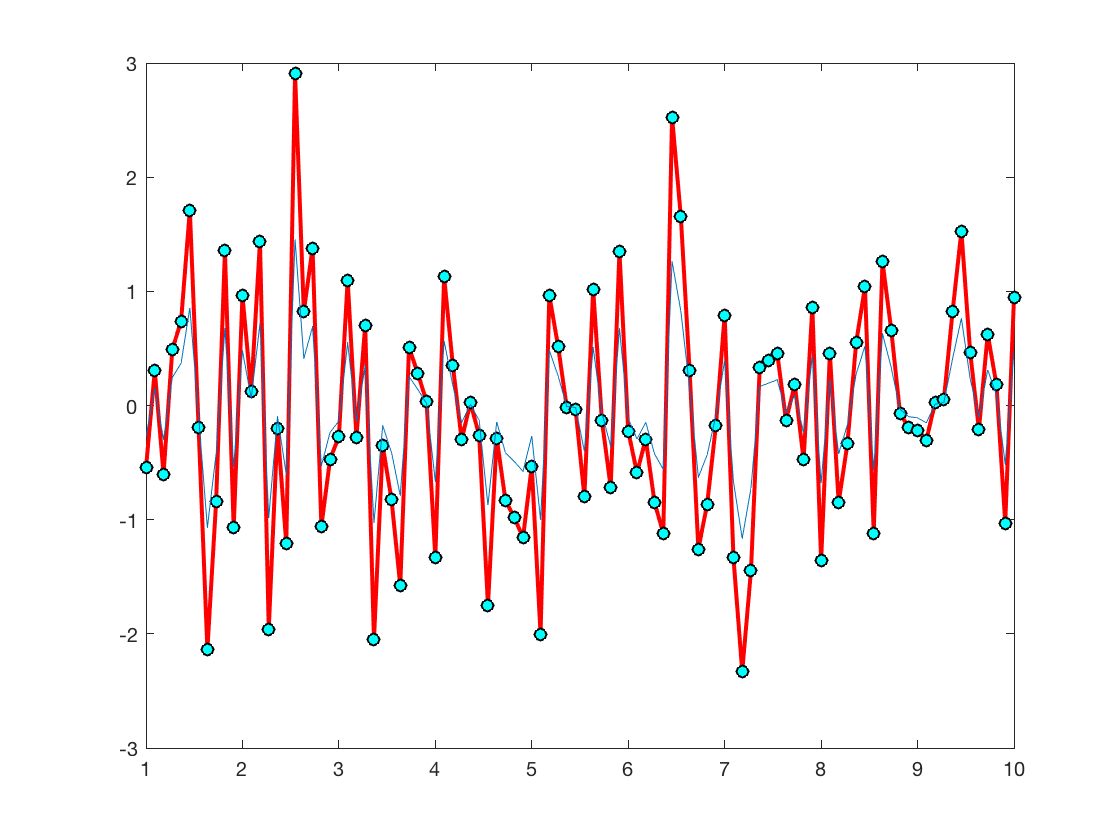
In the code snippet that produces the plot above, here is an explanation in English. First I created a 100-point equally-spaced vector that went from 1 to 10. Then I used randn to make another vector with random entries that is the same length as the first vector. Then I made another vector the same length as the first two whose entries are all half the value of what they were in the second vector. The rest of the snippet is plotting. The line plot(x,y,'r-','linewidth',2); plots x vs. y with a red line two points wide. I use hold on so that the next plot command plots over the first one without clearing the plotting axes. The next plot command plots the same data as before, using a black circle that is filled with cyan. Then the line command plots x vs. z using a blue solid line that is the default. To look up the various colors, symbols, and linestyles do help plot inside the MATLAB command window.

Check yourself!

Summary

add summary here

Reminder - Complete all of the Lesson 2 tasks!

You have reached the end of Lesson 2! Double-check the to-do list on the Lesson 2 Overview page [1] to make sure you have completed all of the activities listed there before you begin Lesson 3.