Prioritize...
Upon completion of this page, you should be able to define vertical wind shear, and discuss its role in convective forecasting. You should also be able to define "bulk shear," and the threshold at which 0-6 kilometer bulk shear is considered strong, increasing the chances of sustained thunderstorm updrafts (including supercells).
Read...
Of all the concepts you'll learn in this course, none has more forecasting utility than the following principle: Vertical wind shear governs the mode (type) of thunderstorms. Thus, vertical wind shear is of huge interest to mesoscale forecasters. After assessing the background synoptic-scale pattern and evaluating CAPE (and CIN) in order to identify regions where thunderstorms will likely be initiated, forecasters routinely turn their attention to vertical wind shear to help them assess what potential types of thunderstorms will develop, and how long-lived they might be. We haven't covered any details yet, but you've already heard me mention that long-lived, rotating updrafts usually form in environments with relatively strong vertical wind shear.
To get an understanding of the importance of vertical wind shear, we need to first learn how to determine vertical wind shear over a fixed point. Then I'll introduce and discuss Rapid Refresh analyses of vertical wind shear between the ground and an altitude of six kilometers, which, as you will also learn in this section, is a crucial layer that forecasters consider whenever supercells are possible.
For starters, as I've mentioned, vertical wind shear is a change in wind speed and/or wind direction with altitude. To get your quantitative bearings, check out this vertical profile of winds, showing an environment with relatively strong vertical wind shear between the ground and six kilometers. Note that wind direction doesn't change very much in the layer, but the dramatic increase in wind speed with height should be obvious. Now, compare the example with strong vertical shear to a vertical profile of winds with weak shear.
So, how do we formally calculate vertical wind shear? Given that the wind is a vector (it has both direction and magnitude), we can calculate vertical wind shear in any given layer of air by taking the wind vector at the top of the layer minus the wind vector at the bottom of the layer (vector subtraction).
Right off the bat, you should see that vertical wind shear is also a vector (the difference between two vectors is a vector). As a vector, vertical wind shear has both magnitude and direction. I realize that many of you aren't accustomed to working with vectors, but we can simplify the vector subtraction by plotting the wind vectors as shown below.

On the graph above (called a "polar coordinate" graph), the circles represent wind speed expressed in knots and the interval between successive circles is 10 knots. The horizontal and vertical axes serve as references for a wind compass so that we can also take wind direction into account.
To start, let's assume that we want to calculate the vertical wind shear vector in a layer of air where the wind at the top of the layer blows from the west-northwest (300 degrees) at 40 knots, while the wind at the bottom of the layer blows from the west-southwest (250 degrees) at 10 knots. To plot the wind vector at the top of the layer, I estimated 300 degrees on the wind compass and judiciously placed a small dot (not shown) on the fourth concentric circle from the origin. Then I drew the vector corresponding to the wind at the top of the layer (bluish) from the origin to the dot. Now for the wind at the bottom of the layer. I estimated 250 degrees on the wind compass and placed a dot (not shown) on the innermost circle and drew the vector (in green).
To subtract the lower wind vector from the upper wind vector, simply draw a vector from the arrowhead of the lower wind vector to the arrowhead of the upper wind vector. Yes, the black vector represents the vertical wind shear vector in the layer. It has magnitude (35 knots) and direction (314 degrees). I'll spare you the trigonometry of how I arrived at that specific numerical answer, but you can at least see how the process works graphically. I also recommend checking out this interactive tool that automatically calculates the vertical wind shear vector for any given layer of air. Exploring this tool will allow you get comfortable with treating vertical wind shear as a vector.
Now that you have an idea of how vertical wind shear is calculated, the big question becomes, "What layer (or layers) of the troposphere is (are) important for predicting whether there will be long-lived, rotating updrafts?"
Cloud-Layer Shear
The answer to the question I just posed is vertical wind shear in the "cloud layer" (the layer encompassing the convective clouds that comprise thunderstorms). For the record, cloud-layer shear is simply the magnitude of the vector difference between the wind at cloud base and the wind at the top of the storm. A couple of aspects of shear within the cloud layer are critically important for thunderstorm forecasting. First, updrafts can be persistent (last longer) when deep-layer wind shear is sufficiently strong. Second, updrafts can begin to rotate (supercells can form) when low-level wind shear is sufficiently strong.
However, the altitudes of cloud bases and cloud tops (particularly the latter) vary from place to place and time to time. For example, the photograph below shows a high-based thunderstorm, which gets its name from a relatively high LCL. Not surprisingly, the depths of storms also vary with location (higher tops in southern Florida compared to southern Canada, for example) and with season (higher tops in summer, for example). Storm depths vary with the synoptic-scale environment as well (no surprise there, either). So, performing an exact cloud-layer shear calculation is quite challenging.
Given the challenges that exist in calculating cloud-layer shear exactly, how do forecasters approach the issue of vertical wind shear when it comes to forecasting deep, moist convection? In order to compare cases from one day to another, or from location to location, forecasters rely on the vertical wind shear between the ground and six kilometers (usually abbreviated 0-6 km shear or sfc-6 km shear) as a standard tool. Of course, 0-6km shear isn't really the same thing as cloud-layer shear, but forecasters often use it as a proxy when thunderstorm updrafts will be surface based (you'll learn later in the lesson that some thunderstorm updrafts don't actually originate at the surface).
Why 0-6 kilometers? Good question! As it turns out, model simulations conducted by the Weisman and Klemp in the 1980s helped to identify the layer between the ground and an altitude near six kilometers as pivotal for predicting thunderstorm type. If you're interested, here's Weisman and Klemp's classic 1982 paper. Although much of this paper is beyond what we've covered so far, by the end of the course, you'll actually be able to comprehend much of Weisman and Klemp's findings! Weisman and Klemp's simulations indicated that thunderstorms tended to be short-lived whenever model environments lacked deep vertical wind shear (strong shear didn't extend to altitudes near six kilometers). Later empirical research confirmed that vertical shear needs to be relatively strong through the lowest five or six kilometers of the troposphere in order for supercells to form.
With that background out of the way, let's take a quick look at an example. On June 5, 2009, the VORTEX2 team intercepted a supercell tornado in Goshen County in southeast Wyoming (YouTube video). At 22Z, the magnitude of the roughly westerly vertical wind shear between the ground and six kilometers was approximately 50 knots (see 22Z analysis below from the national archive at the Storm Prediction Center -- images of sfc-6 km Shear are listed as "shr6"). In real time, you can access regional fields of 0-6 km shear on SPC's Mesoanalysis page (in the "Wind Shear" menu).
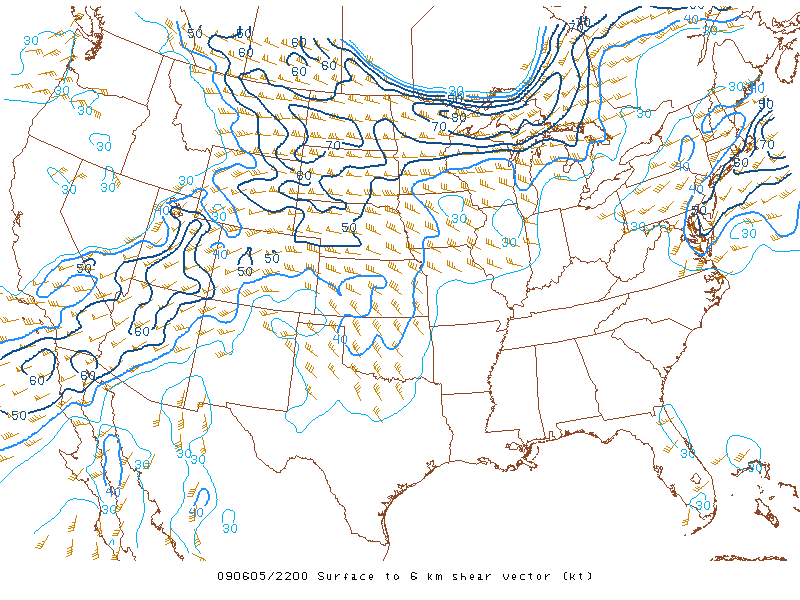
The 50-knot shear magnitude between the surface and six kilometers over Wyoming is a "bulk" shear value, meaning that it's the overall shear between the top and bottom of the layer. Such "bulk" shear calculations do not account for "internal" changes in wind speed and / or direction that occur at intermediate altitudes between the ground and six kilometers. According to the Storm Prediction Center, the threshold of sfc-6 km shear that favors sustained, persistent updrafts (and possibly supercells) is roughly 35-40 knots, so the shear over southeast Wyoming at this time was plenty strong.
However, you shouldn't think of this 35-40 knot threshold for sustained updrafts and supercells as a "hard" threshold. Indeed, persistent updrafts and supercells can sometimes happen with lower magnitudes of 0-6 km shear. Given the right environmental conditions, some experienced forecasters start to consider the possibility of supercells when 0-6 km shear reaches about 20 knots, especially when there was a fairly dramatic change in wind direction between the ground and six kilometers (from the southeast near the surface to westerly or even northwesterly at six kilometers, for example). You will learn later that a dramatic turning of winds (change in wind direction) in the lower troposphere is an important ingredient that favors rotating updrafts.
There's no doubt that a magnitude of 20 knots for 0-6 km shear is way, way below the thresholds you'll see quoted by most sources, but at least thinking about the possibility of supercells in such environments helps to reduce the element of surprise from rare, "unexpected" supercells. The bottom line is that the probability of sustained, rotating updrafts increases markedly near the 35-40 knots quoted by SPC. Therefore, I strongly recommend that you use this more-accepted threshold (35-40 knots) as we move through the rest of the course.
The upshot of this discussion is a basic rule you can take with you: All other factors being equal, the greater the 0-6 km shear, the greater the probability for sustained, rotating storms, especially when there's a dramatic change in wind direction from the ground to six kilometers.
Of course, 0-6 km wind shear doesn't stay "static" in time. It's constantly evolving depending on the synoptic-scale pattern, and those changes are a big forecasting consideration. Now that we've established the importance of variables like CAPE/CIN, environmental lapse rates, and 0-6 km shear, we'll shift gears to look at how the synoptic-scale pattern impacts these fields. Before we move on, however, keep in mind that vertical wind shear isn't just an issue in thunderstorm forecasting. Indeed, interested students may want to check out the Explore Further section below to see how vertical wind shear played a role in a national tragedy.
Explore Further...
Vertical wind shear is critical in thunderstorm forecasting, but it has many other important forecasting applications, as well. In an extreme example of the importance of vertical wind shear, we could say that strong vertical wind shear contributed to a national tragedy. On January 28, 1986, the Space Shuttle Challenger launched from Kennedy Space Center. Below is the 12Z sounding from nearby Cape Canaveral, Florida from the morning of the launch. Note the very cold surface conditions (temperatures below 0 degrees Celsius, or 32 degrees Fahrenheit), as well as the significant vertical wind shear present (particularly changes in wind speed).
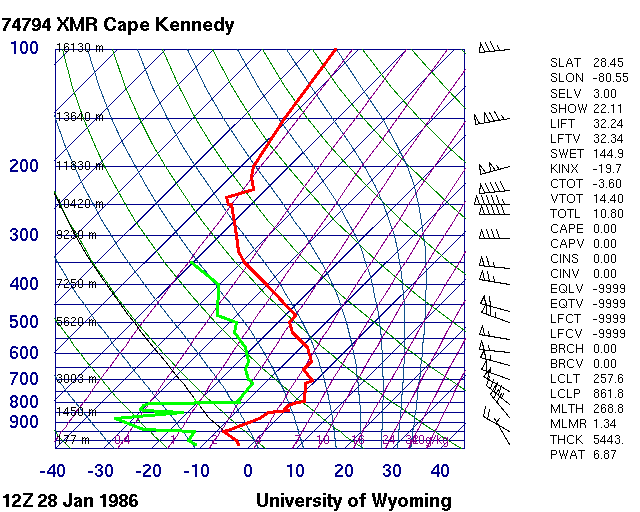
The cold conditions and strong vertical wind shear both conspired with structural deficiencies to cause the shuttle to disintegrate 73 seconds after launch. All seven crew members were killed as millions watched on television. In 2021, Dr. Jon Nese produced the feature for the Penn State Meteorology Department's Weather World program, which described weather's impact on the disaster (below) (3:28 minutes).
[Dr. Jon Nese] Weather has played a pivotal role in many significant events in history, some of them disastrous.
One such incident, 35 years ago tomorrow, vividly sticks with me. I remember exactly where I was when it happened—an event that shattered the stability of the manned U.S. space shuttle program.
The first orbital flight of the shuttle was in April 1981, when Columbia spent a little more than two days in orbit. By mid-January of 1986, another 23 missions had flown using Columbia and three other shuttles: Atlantis, Challenger, and Discovery. Weather had delayed many launches and landings in those years, but there were no catastrophic weather-related problems.
One pesky design issue had dogged many of those early launches. To provide thrust, the shuttle used two solid rocket boosters connected to a large external fuel tank. Each booster had six sections, and some of the joints between sections were sealed by pairs of synthetic rubber gaskets called O-rings. These helped contain the hot, high-pressure gases produced when the fuel burned. These O-rings had leaked during 15 shuttle flights prior to January 1986.
Despite redesign efforts to address the problem, in addition, low temperatures made the rubber O-rings less elastic and thus less likely to properly seal the joints. The tenth flight of shuttle Challenger was originally set for January 22, 1986. It was the highly publicized "first teacher in space" mission, but the launch was delayed until the 28th. That morning was unusually cold, with temperatures in the low 20s at Cape Canaveral. Shuttle launches were prohibited at temperatures below 31 °F, so the launch was pushed back to late morning to allow the atmosphere to warm.
But the unusual chill had already compromised the O-rings on one of the rocket boosters. Analysis of images after the accident showed gray smoke leaking from the booster in the seconds after ignition. At first, the damaged joint was temporarily sealed by residue from some of the burned fuel. But about 30 seconds after launch, the shuttle entered a zone of large wind shear, with speeds increasing from about 70 miles per hour at 20,000 feet to more than 140 miles per hour at 45,000 feet.
In response, the automated steering system made more adjustments than on any previous flight to counter the changing aerodynamic forces on the vehicle. Were it not for this extra maneuvering, the temporary seal on the booster joint might have held. But instead, hot gas began to leak again and eventually flames burned through the strut connecting the booster to the external fuel tank. This started a series of catastrophic events that led to the breakup of the orbiter 73 seconds into flight and the loss of the crew of seven.
The Challenger disaster resulted in a 32-month hiatus in the space shuttle program. Once it resumed in September 1988, 110 more missions flew, including one other non-weather-related catastrophic failure—Columbia in 2003. The final space shuttle mission was nearly 10 years ago, in July 2011.
Stay tuned—our extended forecast is next.