The Nature of Geographic Information
Chapter 1: Data and Information
1. Overview
When I started writing this text in 1997, my office was across the street (and, fortunately, upwind) from Penn State's power plant. The energy used to heat and cool my office is still produced there by burning natural gas extracted from wells in nearby counties. Combustion transforms the potential energy stored in the gas into electricity, which solves the problem of an office that would otherwise be too cold or too warm. Unfortunately, the solution itself causes another problem, namely emissions of carbon dioxide and other more noxious substances into the atmosphere. Cleaner means of generating electricity exist, of course, but they, too, involve transforming energy from one form to another. And cleaner methods cost more than most of us are willing or able to pay.
It seems to me that a coal-fired power plant is a pretty good analogy for a geographic information system. For that matter, GIS is comparable to any factory or machine that transforms a raw material into something more valuable. Data is grist for the GIS mill. GIS is like the machinery that transforms the data into the commodity--information--that is needed to solve problems or create opportunities. And the problems that the manufacturing process itself creates include uncertainties resulting from imperfections in the data, intentional or unintentional misuse of the machinery, and ethical issues related to what the information is used for, and who has access to it.
This text explores the nature of geographic information. To study the nature of something is to investigate its essential characteristics and qualities. To understand the nature of the energy produced in a coal-fired power plant, one should study the properties, morphology, and geographic distribution of coal. By the same reasoning, I believe that a good approach to understanding the information produced by GIS is to investigate the properties of geographic data and the technologies and institutions that produce it.
Objectives
The goal of Chapter 1 is to situate GIS in a larger enterprise known as Geographic Information Science and Technology (GIS&T), and in what the U.S. Department of Labor calls the "geospatial industry." In particular, students who successfully complete Chapter 1 should be able to:
- define a geographic information system;
- recognize and name basic database operations from verbal descriptions;
- recognize and name basic approaches to geographic representation from verbal descriptions;
- identify and explain at least three distinguishing properties of geographic data; and
- outline the kinds of questions that GIS can help answer.
"Try This!" Activities
Take a minute to complete any of the Try This activities that you encounter throughout the chapter. These are fun, thought-provoking exercises to help you better understand the ideas presented in the chapter.

2. Data
"After more than 30 years, we're still confronted by the same major challenge that GIS professionals have always faced: You must have good data. And good data are expensive and difficult to create." (Wilson, 2001, p. 54)
Data consist of symbols that represent measurements of phenomena. People create and study data as a means to help understand how natural and social systems work. Such systems can be hard to study because they're made up of many interacting phenomena that are often difficult to observe directly and because they tend to change over time. We attempt to make systems and phenomena easier to study by measuring their characteristics at certain times. Because it's not practical to measure everything, everywhere, at all times, we measure selectively. How accurately data reflect the phenomena they represent depends on how, when, where, and what aspects of the phenomena were measured. All measurements, however, contain a certain amount of error.
Measurements of the locations and characteristics of phenomena can be represented with several different kinds of symbols. For example, pictures of the land surface, including photographs and maps, are made up of graphic symbols. Verbal descriptions of property boundaries are recorded on deeds using alphanumeric symbols. Locations determined by satellite positioning systems are reported as pairs of numbers called coordinates. As you probably know, all of these different types of data--pictures, words, and numbers--can be represented in computers in digital form. Obviously, digital data can be stored, transmitted, and processed much more efficiently than their physical counterparts that are printed on paper. These advantages set the stage for the development and widespread adoption of GIS.
3. Information
Information is data that has been selected or created in response to a question. For example, the location of a building or a route is data, until it is needed to dispatch an ambulance in response to an emergency. When used to inform those who need to know, "Where is the emergency, and what's the fastest route between here and there?" the data are transformed into information. The transformation involves the ability to ask the right kind of question, and the ability to retrieve existing data--or to generate new data from the old--that help people answer the question. The more complex the question and the more locations involved, the harder it becomes to produce timely information with paper maps alone.
Interestingly, the potential value of data is not necessarily lost when they are used. Data can be transformed into information again and again, provided that the data are kept up to date. Given the rapidly increasing accessibility of computers and communications networks in the U.S. and abroad, it's not surprising that information has become a commodity, and that the ability to produce it has become a major growth industry.
4. Information Systems
Information systems are computer-based tools that help people transform data into information.
As you know, many of the problems and opportunities faced by government agencies, businesses, and other organizations are so complex, and involve so many locations, that the organizations need assistance in creating useful and timely information. That's what information systems are for.
Allow me a fanciful example. Suppose that you've launched a new business that manufactures solar-powered lawn mowers. You're planning a direct mail campaign to bring this revolutionary new product to the attention of prospective buyers. But, since it's a small business, you can't afford to sponsor coast-to-coast television commercials or to send brochures by mail to more than 100 million U.S. households. Instead, you plan to target the most likely customers - those who are environmentally conscious, have higher than average family incomes, and who live in areas where there is enough water and sunshine to support lawns and solar power.
Fortunately, lots of data are available to help you define your mailing list. Household incomes are routinely reported to banks and other financial institutions when families apply for mortgages, loans, and credit cards. Personal tastes related to issues like the environment are reflected in behaviors such as magazine subscriptions and credit card purchases. Firms like Claritas amass such data and transform it into information by creating "lifestyle segments" - categories of households that have similar incomes and tastes. Your solar lawnmower company can purchase lifestyle segment information by 5-digit ZIP code, or even by ZIP+4 codes, which designate individual households.
It's astonishing how companies like Claritas, Experian, and Esri can create valuable information from the millions upon millions of transactions that are recorded every day. Their "lifestyle segmentation" data products are made possible by the fact that the original data exist in digital form, and because the companies have developed information systems that enable them to transform the data into information that marketers value. The fact that lifestyle information products are often delivered by geographic areas, such as ZIP codes, speaks to the appeal of geographic information systems.
Try This!
How does your ZIP code look to marketers?
Lifestyle segmentation data cluster similar households into lifestyle categories - “segments” - that marketers can use to target advertising. Lifestyle segments have evocative names like “Gen X Urban,” “Senior Styles,” and “Rustic Outposts." For example, according to Esri’s Tapestry Segmentation, the predominant lifestyle groups in my ZIP code are Down the Road, Soccer Moms, and Exurbanites.
You can use Esri’s ZIP Lookup to see how your ZIP code is segmented. Do the lifestyle segments seem accurate for your community? If you don't live in the United States, try Penn State's Zip code, 16802.

5. Databases, Mapping, and GIS
One of our objectives in this first chapter is to be able to define a geographic information system. Here's a tentative definition: A GIS is a computer-based tool used to help people transform geographic data into geographic information.
The definition implies that a GIS is somehow different from other information systems, and that geographic data are different from non-geographic data. Let's consider the differences next.
6. Database Management Systems
Claritas and similar companies use database management systems (DBMS) to create the "lifestyle segments" that I referred to in the previous section. Basic database concepts are important since GIS incorporates much of the functionality of DBMS.
Digital data are stored in computers as files. Often, data are arrayed in tabular form. For this reason, data files are often called tables. A database is a collection of tables. Businesses and government agencies that serve large clienteles, such as telecommunications companies, airlines, credit card firms, and banks, rely on extensive databases for their billing, payroll, inventory, and marketing operations. Database management systems are information systems that people use to store, update, and analyze non-geographic databases.
Often, data files are tabular in form, composed of rows and columns. Rows, also known as records, correspond with individual entities, such as customer accounts. Columns correspond with the various attributes associated with each entity. The attributes stored in the accounts database of a telecommunications company, for example, might include customer names, telephone numbers, addresses, current charges for local calls, long distance calls, taxes, etc.
Geographic data are a special case: records correspond with places, not people or accounts. Columns represent the attributes of places. The data in the following table, for example, consist of records for Pennsylvania counties. Columns contain selected attributes of each county, including the county's ID code, name, and 1980 population.
| FIPS Code | County | 1980 Pop |
|---|---|---|
| 42001 | Adams County | 78274 |
| 42003 | Allegheny County | 1336449 |
| 42005 | Armstrong County | 73478 |
| 42007 | Beaver County | 186093 |
| 42009 | Bedford County | 47919 |
| 42011 | Berks County | 336523 |
| 42013 | Blair County | 130542 |
| 42015 | Bradford County | 60967 |
| 42017 | Bucks County | 541174 |
| 42019 | Butler County | 152013 |
| 42021 | Cambria County | 163062 |
| 42023 | Cameron County | 5913 |
| 42025 | Carbon County | 56846 |
| 42027 | Centre County | 124812 |
Table 1.1: The contents of one file in a database.
The example is a very simple file, but many geographic attribute databases are in fact very large (the U.S. is made up of over 3,000 counties, almost 50,000 census tracts, about 43,000 five-digit ZIP code areas and many tens of thousands more ZIP+4 code areas). Large databases consist not only of lots of data, but also lots of files. Unlike a spreadsheet, which performs calculations only on data that are present in a single document, database management systems allow users to store data in, and retrieve data from, many separate files. For example, suppose an analyst wished to calculate population change for Pennsylvania counties between the 1980 and 1990 censuses. More than likely, 1990 population data would exist in a separate file, like so:
| FIPS Code | 1990 Pop |
|---|---|
| 42001 | 84921 |
| 42003 | 1296037 |
| 42005 | 73872 |
| 42007 | 187009 |
| 42009 | 49322 |
| 42011 | 352353 |
| 42013 | 131450 |
| 42015 | 62352 |
| 42017 | 578715 |
| 42019 | 167732 |
| 42021 | 158500 |
| 42023 | 5745 |
| 42025 | 58783 |
| 42027 | 131489 |
Table 1.2: Another file in a database. A database management system (DBMS) can relate this file to the prior one illustrated above because they share the list of attributes called "FIPS Code."
If two data files have at least one common attribute, a DBMS can combine them in a single new file. The common attribute is called a key. In this example, the key was the county FIPS code (FIPS stands for Federal Information Processing Standard). The DBMS allows users to produce new data as well as to retrieve existing data, as suggested by the new "% Change" attribute in the table below.
| FIPS | County | 1980 | 1990 | % Change |
|---|---|---|---|---|
| 42001 | Adams | 78274 | 84921 | 8.5 |
| 42003 | Allegheny | 1336449 | 1296037 | -3 |
| 42005 | Armstrong | 73478 | 73872 | 0.5 |
| 42007 | Beaver | 186093 | 187009 | 0.5 |
| 42009 | Bedford | 47919 | 49322 | 2.9 |
| 42011 | Berks | 336523 | 352353 | 4.7 |
| 42013 | Blair | 130542 | 131450 | 0.7 |
| 42015 | Bradford | 60967 | 62352 | 2.3 |
| 42017 | Bucks | 541174 | 578715 | 6.9 |
| 42019 | Butler | 152013 | 167732 | 10.3 |
| 42021 | Cambria | 163062 | 158500 | -2.8 |
| 42023 | Cameron | 5913 | 5745 | -2.8 |
| 42025 | Carbon | 56846 | 58783 | 3.4 |
| 42027 | Centre | 124812 | 131489 | 5.3 |
Table 1.3: A new file produced from the prior two files as a result of two database operations. One operation merged the contents of the two files without redundancy. A second operation produced a new attribute--"% Change"--dividing the difference between "1990 Pop" and "1980 Pop" by "1980 Pop" and expressing the result as a percentage.
Database management systems are valuable because they provide secure means of storing and updating data. Database administrators can protect files so that only authorized users can make changes. DBMS provide transaction management functions that allow multiple users to edit the database simultaneously. In addition, DBMS also provide sophisticated means to retrieve data that meet user specified criteria. In other words, they enable users to select data in response to particular questions. A question that is addressed to a database through a DBMS is called a query.
Database queries include basic set operations, including union, intersection, and difference. The product of a union of two or more data files is a single file that includes all records and attributes, without redundancy. An intersection produces a data file that contains only records present in all files. A difference operation produces a data file that eliminates records that appear in both original files. (Try drawing Venn diagrams--intersecting circles that show relationships between two or more entities--to illustrate the three operations. Then compare your sketch to the venn diagram example. ) All operations that involve multiple data files rely on the fact that all files contain a common key. The key allows the database system to relate the separate files. Databases that contain numerous files that share one or more keys are called relational databases. Database systems that enable users to produce information from relational databases are called relational database management systems.
A common use of database queries is to identify subsets of records that meet criteria established by the user. For example, a credit card company may wish to identify all accounts that are 30 days or more past due. A county tax assessor may need to list all properties not assessed within the past 10 years. Or the U.S. Census Bureau may wish to identify all addresses that need to be visited by census takers, because census questionnaires were not returned by mail. DBMS software vendors have adopted a standardized language called SQL (Structured Query Language) to pose such queries.

7. Mapping Systems
GIS (geographic information systems) arose out of the need to perform spatial queries on geographic data. A spatial query requires knowledge of locations as well as attributes. For example, an environmental analyst might want to know which public drinking water sources are located within one mile of a known toxic chemical spill. Or, a planner might be called upon to identify property parcels located in areas that are subject to flooding. To accommodate geographic data and spatial queries, database management systems need to be integrated with mapping systems. Until about 1990, most maps were printed from handmade drawings or engravings. Geographic data produced by draftspersons consisted of graphic marks inscribed on paper or film. To this day, most of the lines that appear on topographic maps published by the U.S. Geological Survey were originally engraved by hand. The place names shown on the maps were affixed with tweezers, one word at a time. Needless to say, such maps were expensive to create and to keep up to date. Computerization of the mapmaking process had obvious appeal.
Computer-aided design (CAD) CAD systems were originally developed for engineers, architects, and other design professionals who needed more efficient means to create and revise precise drawings of machine parts, construction plans, and the like. In the 1980s, mapmakers began to adopt CAD in place of traditional map drafting. CAD operators encode the locations and extents of roads, streams, boundaries, and other entities by tracing maps mounted on electronic drafting tables, or by key-entering location coordinates, angles, and distances. Instead of graphic features, CAD data consist of digital features, each of which is composed of a set of point locations. Calculations of distances, areas, and volumes can easily be automated once features are digitized. Unfortunately, CAD systems typically do not encode data in forms that support spatial queries. In 1988, a geographer named David Cowen illustrated the benefits and shortcomings of CAD for spatial decision making. He pointed out that a CAD system would be useful for depicting the streets, property parcel boundaries, and building footprints of a residential subdevelopment. A CAD operator could point to a particular parcel, and highlight it with a selected color or pattern. "A typical CAD system," Cowen observed, "could not automatically shade each parcel based on values in an assessor's database containing information regarding ownership, usage, or value, however." A CAD system would be of limited use to someone who had to make decisions about land use policy or tax assessment.
Desktop mapping An evolutionary stage in the development of GIS, desktop mapping systems like Atlas*GIS combined some of the capabilities of CAD systems with rudimentary linkages between location data and attribute data. A desktop mapping system user could produce a map in which property parcels are automatically colored according to various categories of property values, for example. Furthermore, if property value categories were redefined, the map's appearance could be updated automatically. Some desktop mapping systems even supported simple queries that allow users to retrieve records from a single attribute file. Most real-world decisions require more sophisticated queries involving multiple data files. That's where real GIS comes in.
Geographic information systems (GIS) As stated earlier, information systems assist decision makers by enabling them to transform data into useful information. GIS specializes in helping users transform geographic data into geographic information. David Cowen (1988) defined GIS as a decision support tool that combines the attribute data handling capabilities of relational database management systems with the spatial data handling capabilities of CAD and desktop mapping systems. In particular, GIS enables decision makers to identify locations or routes whose attributes match multiple criteria, even though entities and attributes may be encoded in many different data files.
Innovators in many fields, including engineers, computer scientists, geographers, and others, started developing digital mapping and CAD systems in the 1950s and 60s. One of the first challenges they faced was to convert the graphical data stored on paper maps into digital data that could be stored in, and processed by, digital computers. Several different approaches to representing locations and extents in digital form were developed. The two predominant representation strategies are known as "vector" and "raster."
8. Representation Strategies for Mapping
Recall that data consist of symbols that represent measurements. Digital geographic data are encoded as alphanumeric symbols that represent locations and attributes of locations measured at or near Earth's surface. No geographic data set represents every possible location, of course. The Earth is too big, and the number of unique locations is too great. In much the same way that public opinion is measured through polls, geographic data are constructed by measuring representative samples of locations. And just as serious opinion polls are based on sound principles of statistical sampling, so, too, do geographic data represent reality by measuring carefully chosen samples of locations. Vector and raster data are, at essence, two distinct sampling strategies.
The vector approach involves sampling locations at intervals along the length of linear entities (like roads), or around the perimeter of areal entities (like property parcels). When they are connected by lines, the sampled points form line features and polygon features that approximate the shapes of their real-world counterparts.

Try This!
Click the graphic above (Figure 1.9.1) to download and view the animation file (vector.avi, 1.6 Mb) in a separate Microsoft Media Player window.
To download and view the same animation in QuickTime format (vector.mov, 1.6 Mb), click here. Requires QuickTime, which is available free at apple.com.
The aerial photograph above (Figure 1.9.1) shows two entities, a reservoir and a highway. The graphic above right illustrates how the entities might be represented with vector data. The small squares are nodes: point locations specified by latitude and longitude coordinates. Line segments connect nodes to form line features. In this case, the line feature colored red represents the highway. Series of line segments that begin and end at the same node form polygon features. In this case, two polygons (filled with blue) represent the reservoir.
The vector data model is consistent with how surveyors measure locations at intervals as they traverse a property boundary. Computer-aided drafting (CAD) software used by surveyors, engineers, and others, stores data in vector form. CAD operators encode the locations and extents of entities by tracing maps mounted on electronic drafting tables, or by key-entering location coordinates, angles, and distances. Instead of graphic features, CAD data consist of digital features, each of which is composed of a set of point locations.
The vector strategy is well suited to mapping entities with well-defined edges, such as highways or pipelines or property parcels. Many of the features shown on paper maps, including contour lines, transportation routes, and political boundaries, can be represented effectively in digital form using the vector data model.
The raster approach involves sampling attributes at fixed intervals. Each sample represents one cell in a checkerboard-shaped grid.

Try This!
Click the graphic above (Figure 1.9.2) to download and view the animation file (raster.avi, 0.8 Mb) in a separate Microsoft Media Player window.
To download and view the same animation in QuickTime format (raster.mov, 0.6 Mb), click here. Requires QuickTime, which is available free at apple.com.
The graphic above (Figure 1.9.2) illustrates a raster representation of the same reservoir and highway as shown in the vector representation. The area covered by the aerial photograph has been divided into a grid. Every grid cell that overlaps one of the two selected entities is encoded with an attribute that associates it with the entity it represents. Actual raster data would not consist of a picture of red and blue grid cells, of course; they would consist of a list of numbers, one number for each grid cell, each number representing an entity. For example, grid cells that represent the highway might be coded with the number "1" and grid cells representing the reservoir might be coded with the number "2."
The raster strategy is a smart choice for representing phenomena that lack clear-cut boundaries, such as terrain elevation, vegetation, and precipitation. Digital airborne imaging systems, which are replacing photographic cameras as primary sources of detailed geographic data, produce raster data by scanning the Earth's surface pixel by pixel and row by row.
Both the vector and raster approaches accomplish the same thing: they allow us to caricature the Earth's surface with a limited number of locations. What distinguishes the two is the sampling strategies they embody. The vector approach is like creating a picture of a landscape with shards of stained glass cut to various shapes and sizes. The raster approach, by contrast, is more like creating a mosaic with tiles of uniform size. Neither is well suited to all applications, however. Several variations on the vector and raster themes are in use for specialized applications, and the development of new object-oriented approaches is underway.

9. Automated Map Analysis
As I mentioned earlier, the original motivation for developing computer mapping systems was to automate the map making process. Computerization has not only made map making more efficient, it has also removed some of the technological barriers that used to prevent people from making maps themselves. What used to be an arcane craft practiced by a few specialists has become a "cloud" application available to any networked computer user. When I first started writing this text in 1997, my example was the mapping extension included in Microsoft Excel 97, which made creating a simple map as easy as creating a graph. Seventeen years later, who hasn't used Google Maps or MapQuest?
As much as computerization has changed the way maps are made, it has had an even greater impact on how maps can be used. Calculations of distance, direction, and area, for example, are tedious and error-prone operations with paper maps. Given a digital map, such calculations can easily be automated. Those who are familiar with CAD systems know this from first-hand experience. Highway engineers, for example, rely on aerial imagery and digital mapping systems to estimate project costs by calculating the volumes of rock that need to be excavated from hillsides and filled into valleys.
The ability to automate analytical tasks not only relieves tedium and reduces errors; it also allows us to perform tasks that would otherwise seem impractical. Consider, for example, if you were asked to plot on a map a 100-meter-wide buffer zone surrounding a protected stream. If all you had to work with was a paper map, a ruler, and a pencil, you might have a lengthy job on your hands. You might draw lines scaled to represent 100 meters, perpendicular to the river on both sides, at intervals that vary in frequency with the sinuosity of the stream. Then you might plot a perimeter that connects the end points of the perpendicular lines. If your task was to create hundreds of such buffer zones, you might conclude that automation is a necessity, not just a luxury.

Some tasks can be implemented equally well in either vector- or raster- oriented mapping systems. Other tasks are better suited to one representation strategy or another. The calculation of slope, for example, or of gradient--the direction of the maximum slope along a surface--is more efficiently accomplished with raster data. The slope of one raster grid cell may be calculated by comparing its elevation to the elevations of the eight cells that surround it. Raster data are also preferred for a procedure called viewshed analysis that predicts which portions of a landscape will be in view, or hidden from view, from a particular perspective.
Some mapping systems provide ways to analyze attribute data as well as locational data. For example, the Excel mapping extension I mentioned above links the geographic data display capabilities of a mapping system with the data analysis capabilities of a spreadsheet. As you probably know, spreadsheets like Excel let users perform calculations on individual fields, columns, or entire files. A value changed in one field automatically changes values throughout the spreadsheet. Arithmetic, financial, statistical, and even certain database functions are supported. But as useful as spreadsheets are, they were not engineered to provide secure means of managing and analyzing large databases that consist of many related files, each of which is the responsibility of a different part of an organization. A spreadsheet is not a DBMS. And, by the same token, a mapping system is not a GIS.
10. Geographic Information Systems
The preceding discussion leads me to revise my working definition:
As I mentioned earlier, a geographer named David Cowen defined GIS as a decision-support tool that combines the capabilities of a relational database management system with the capabilities of a mapping system (1988). Cowen cited an earlier study by William Carstensen (1986), who sought to establish criteria by which local governments might choose among competing GIS products. Carstensen chose site selection as an example of the kind of complex task that many organizations seek to accomplish with GIS. Given the necessary database, he advised local governments to expect that a fully functional GIS should be able to identify property parcels that are:
- at least five acres in size;
- vacant or for sale;
- zoned commercial;
- not subject to flooding;
- located not more than one mile from a heavy duty road; and
- situated on terrain whose maximum slope is less than ten percent.
The first criterion--identifying parcels five acres or more in size--might require two operations. As described earlier, a mapping system ought to be able to calculate automatically the area of a parcel. Once the area is calculated and added as a new attribute into the database, an ordinary database query could produce a list of parcels that satisfy the size criterion. The parcels on the list might also be highlighted on a map, as in Figure 1.11.1, below.

The ownership status of individual parcels would be an attribute of a property database maintained by a local tax assessor's office. Parcels whose ownership status attribute value matched the criteria "vacant" or "for sale" could be identified through another ordinary database query.

Carstensen's third criterion was to determine which parcels were situated within areas zoned for commercial development. This would be simple if authorized land uses were included as an attribute in the community's property parcel database. This is unlikely to be the case, however, since zoning and taxation are the responsibilities of different agencies. Typically, parcels and land use zones exist as separate paper maps. If the maps were prepared at the same scale, and if they accounted for the shape of the Earth in the same manner, then they could be superimposed one over another on a light table. If the maps let enough light through, parcels located within commercial zones could be identified.
The GIS approach to a task like this begins by digitizing the paper maps, and by producing corresponding attribute data files. Each digital map and attribute data file is stored in the GIS separately, like separate map layers. A fully functional GIS would then be used to perform a spatial intersection that is analogous to the overlay of the paper maps. Spatial intersection, otherwise known as map overlay, is one of the defining capabilities of GIS.

Another of Carstensen's criteria was to identify parcels located within one mile of a heavy-duty highway. Such a task requires a digital map and associated attributes produced in such a way as to allow heavy-duty highways to be differentiated from other geographic entities. Once the necessary database is in place, a buffer operation can be used to create a polygon feature whose perimeter surrounds all "heavy duty highway" features at the specified distance. A spatial intersection is then performed, isolating the parcels within the buffer from those outside the buffer.
To produce a final list of parcels that meet all the site selection criteria, the GIS analyst might perform an intersection operation that creates a new file containing only those records that are present in all the other intermediate results.

I created the maps shown above in 1998 using the Geographic Information Web Server of the City of Ontario, California. Although it is no longer supported, the City of Ontario was one of the first of its kind to provide much of the functionality required to perform a site suitability analysis online. Today, many local governments offer similar Internet map services to current and prospective taxpayers.
Try This!
Find an online site selection utility similar to the one formerly provided by the City of Ontario.

11. Geographic Information Science and Technology
So far in this chapter, I've tried to make sense of GIS in relation to several information technologies, including database management, computer-aided design, and mapping systems. At this point, I'd like to expand the discussion to consider GIS as one element in a much larger field of study called "Geographic Information Science and Technology" (GIS&T). As shown in the following illustration, GIS&T encompasses three subfields including:
- Geographic Information Science, the multidisciplinary research enterprise that addresses the nature of geographic information and the application of geospatial technologies to basic scientific questions;
- Geospatial Technology, the specialized set of information technologies that support acquisition, management, analysis, and visualization of geo-referenced data, including the Global Navigation Satellite System (GPS and others), satellite, airborne, and shipboard remote sensing systems; and GIS and image analysis software tools; and
- Applications of GIS&T, the increasingly diverse uses of geospatial technology in government, industry, and academia.This is the subfield in which most GIS professionals work.
Arrows in the diagram below (Figure 1.12.1) reflect relationships among the three subfields, as well as to numerous other fields, including Geography, Landscape Architecture, Computer Science, Statistics, Engineering, and many others. Each of these fields has influenced, and some have been influenced by, the development of GIS&T. It is important to note that these fields and subfields do not neatly correspond with professions like GIS analyst, photogrammetrist, or land surveyor. Rather, GIS&T is a nexus of overlapping professions that differ in backgrounds, disciplinary allegiances, and regulatory status.

Related Disciplines to Geographic Information Science and Technology:
- Philosophy
- Psychology
- Mathematics
- Statistics
- Computer Science
- Geography
- Information Science & Technology
- Geospatial Technology
- Engineering
- Landscape Architecture
- Various Application Domains
The illustration in Figure 1.12.1, above, first appeared in the Geographic Information Science and Technology Body of Knowledge (DiBiase, DeMers, Johnson, Kemp, Luck, Plewe, and Wentz, 2006), published by the University Consortium for Geographic Information Science (UCGIS) and the Association of American Geographers (AAG) in 2006. The Body of Knowledge is a community-developed inventory of the knowledge and skills that define the GIS&T field. Like the bodies of knowledge developed in Computer Science and other fields, the GIS&T BoK represents the GIS&T knowledge domain as a hierarchical list of knowledge areas, units, topics, and educational objectives. The ten knowledge areas and 73 units that make up the first edition are shown in the table below. Twenty-six “core” units (those in which all graduates of a degree or certificate program should be able to demonstrate some level of mastery) are shown in bold type. Not shown are the 329 topics that make up the units, or the 1,660 education objectives by which topics are defined. These appear in the full text of the GIS&T BoK. The full text of the first edition can be found here: GIST Body of Knowledge PDF. An important related work produced by the U.S. Department of Labor is, however. We'll take a look at that shortly.
Knowledge Areas and Units Comprising the 1st Edition of the GIS&T BoK
- Knowledge Area AM. Analytical Methods
- Unit AM1 Academic and analytical origins
- Unit AM2 Query operations and query languages
- Unit AM3 Geometric measures
- Unit AM4 Basic analytical operations
- Unit AM5 Basic analytical methods
- Unit AM6 Analysis of surfaces
- Unit AM7 Spatial statistics
- Unit AM8 Geostatistics
- Unit AM9 Spatial regression and econometrics
- Unit AM10 Data mining
- Unit AM11 Network analysis
- Unit AM12 Optimization and location
- allocation modeling
- Knowledge Area CF. Conceptual Foundations
- Unit CF1 Philosophical foundations
- Unit CF2 Cognitive and social foundations
- Unit CF3 Domains of geographic information
- Unit CF4 Elements of geographic information
- Unit CF5 Relationships
- Unit CF6 Imperfections in geographic information
- Knowledge Area CV. Cartography and Visualization
- Unit CV1 History and trends
- Unit CV2 Data considerations
- Unit CV3 Principles of map design
- Unit CV4 Graphic representation techniques
- Unit CV5 Map production
- Unit CV6 Map use and evaluation
- Knowledge Area DA. Design Aspects
- Unit DA1 The scope of GI S&T system design
- Unit DA2 Project definition
- Unit DA3 Resource planning
- Unit DA4 Database design
- Unit DA5 Analysis design
- Unit DA6 Application design
- Unit DA7 System implementation
- Knowledge Area DM. Data Modeling
- Unit DM1 Basic storage and retrieval structures
- Unit DM2 Database management systems
- Unit DM3 Tessellation data models
- Unit DM4 Vector and object data models
- Unit DM5 Modeling 3D, temporal, and uncertain phenomena
- Knowledge Area DN. Data Manipulation
- Unit DN1 Representation transformation
- Unit DN2 Generalization and aggregation
- Unit DN3 Transaction management of geospatial data
- Knowledge Area GC. Geocomputation
- Unit GC1 Emergence of geocomputation
- Unit GC2 Computational aspects and neurocomputing
- Unit GC3 Cellular Automata (CA) models
- Unit GC4 Heuristics
- Unit GC5 Genetic algorithms (GA)
- Unit GC6 Agent-based models
- Unit GC7 Simulation modeling
- Unit GC8 Uncertainty
- Unit GC9 Fuzzy sets
- Knowledge Area GD. Geospatial Data
- Unit GD1 Earth geometry
- Unit GD2 Land partitioning systems
- Unit GD3 Georeferencing systems
- Unit GD4 Datums
- Unit GD5 Map projections
- Unit GD6 Data quality
- Unit GD7 Land surveying and GPS
- Unit GD8 Digitizing
- Unit GD9 Field data collection
- Unit GD10 Aerial imaging and photogrammetry
- Unit GD11 Satellite and shipboard remote sensing
- Unit GD12 Metadata, standards, and infrastructures
- Knowledge Area GS. GIS&T and Society
- Unit GS1 Legal aspects
- Unit GS2 Economic aspects
- Unit GS3 Use of geospatial information in the public sector
- Unit GS4 Geospatial information as property
- Unit GS5 Dissemination of geospatial information
- Unit GS6 Ethical aspects of geospatial information and technology
- Unit GS7 Critical GIS
- Knowledge Area OI. Organizational and Institutional Aspects
- Unit OI1 Origins of GI S&T
- Unit O2 Managing the GI system operations and infrastructure
- Unit OI3 Organizational structures and procedures
- Unit OI4 GI S&T workforce themes
- Unit OI5 Institutional and inter-institutional aspects
- Unit OI6 Coordinating organizations (national and international)
Ten knowledge areas and 73 units comprising the 1st edition of the GIS&T BoK. Core units are indicated with bold type. (©2006 Association of American Geographers and University Consortium for Geographic Information Science. Used by permission. All rights reserved.)
Notice that the knowledge area that includes the most core units is GD: Geospatial Data. This text focuses on the sources and distinctive characteristics of geographic data. This is one part of the knowledge base that most successful geospatial professionals possess. The Department of Labor's Geospatial Technology Competency Model (GTCM) highlights this and other essential elements of the geospatial knowledge base. We'll consider it next.
12. Geospatial Competencies and Our Curriculum
A body of knowledge is one way to think about the GIS&T field. Another way is as an industry made up of agencies and firms that produce and consume goods and services, generate sales and (sometimes) profits, and employ people. In 2003, the U.S. Department of Labor (DoL) identified "geospatial technology" as one of 14 "high growth" technology industries, along with biotech, nanotech, and others. However, the DoL also observed that the geospatial technology industry was ill-defined, and poorly understood by the public.
Subsequent efforts by the DoL and other organizations helped to clarify the industry's nature and scope. Following a series of "roundtable" discussions involving industry thought leaders, the Geospatial Information Technology Association (GITA) and the Association of American Geographers (AAG) submitted the following "concensus" definition to DoL in 2006:
The geospatial industry acquires, integrates, manages, analyzes, maps, distributes, and uses geographic, temporal, and spatial information and knowledge. The industry includes basic and applied research, technology development, education, and applications to address the planning, decision making, and operational needs of people and organizations of all types.
In addition to the proposed industry definition, the GITA and AAG report recommended that DoL establish additional occupations in recognition of geospatial industry workforce activities and needs. At the time, the existing geospatial occupations included only Surveyors, Surveying Technicians, Mapping Technicians, and Cartographers and Photogrammetrists. Late in 2009, with input from the GITA, AAG, and other stakeholders, the DoL established six new geospatial occupations: Geospatial Information Scientists and Technologists, Geographic Information Systems Technicians, Remote Sensing Scientists and Technologists, Remote Sensing Technicians, Precision Agriculture Technicians, and Geodetic Surveyors.
Try This!
Investigate the geospatial occupations at the U.S. Department of Labor's "O*Net" database. Enter "geospatial" in the search field named "Occupation Quick Search." Follow links to occupation descriptions. Note the estimates for 2008 employment and employment growth through 2018. Also note that, for some anomalous reason, the keyword "geospatial" is not associated with the occupation "Geodetic Surveyor."

Meanwhile, DoL commenced a "competency modeling" initiative for high-growth industries in 2005. Their goal was to help educational institutions like ours meet the demand for qualified technology workers by identifying what workers need to know and be able to do. At DoL, a competency is "the capability to apply or use a set of related knowledge, skills, and abilities required to successfully perform ‘critical work functions’ or tasks in a defined work setting” (Ennis 2008). A competency model is "a collection of competencies that together define successful performance in a particular work setting."
Workforce analysts at DoL began work on a Geospatial Technology Competency Model (GTCM) in 2005. Building on their research, a panel of accomplished practitioners and educators produced a complete draft of the GTCM, which they subsequently revised in response to public comments. Published in June 2010, the GTCM identifies the competencies that characterize successful workers in the geospatial industry. In contrast to GIS&T Body of Knowledge, an academic project meant to define the nature and scope of the field, the GTCM is an industry specification that defines what individual workers and students should aspire to know and learn.
Try This!
Explore the Geospatial Technology Competency Model (GTCM) at the U.S. Department of Labor's Competency Model Clearinghouse. Under "Industry Competency Models," follow the link "Geospatial Technology." There, the pyramid (shown in Figure 1.13.2, below) is an image map which you can click to reveal the various competencies. The complete GTCM is also available as a Word doc and PDF file.
The GTCM specifies several "tiers" of competencies, progressing from general to occupationally specific. Tiers 1 through 3 (the gray and red layers), called Foundation Competencies, specify general workplace behaviors and knowledge that successful workers in most industries exhibit. Tiers 4 and 5 (yellow) include the distinctive technical competencies that characterize a given industry and its three sectors: Positioning and Data Acquisition, Analysis and Modeling, and Programming and Application Development. Above Tier 5 are additional Tiers corresponding to the occupation-specific competencies and requirements that are specified in the occupation descriptions published at O*NET Online and in a Geospatial Management Competency Model that is in development as of January, 2012.

One way educational institutions and students can use the GTCM is as a guideline for assessing how well curricula align with workforce needs. The Penn State Online GIS program conducted such an assessment in 2011. Results, appear in the spreadsheet linked below.
Try This!
Open the attached Excel spreadsheet to see how our Penn State Online GIS curricula address workforce needs identified in the GTCM.
The sheet will open on a cover page. At the bottom of the sheet are tabs that correspond to Tiers 1-5 of the GTCM. Click the tabs to view the worksheet associated with the Tier you want to see.
In each Tier worksheet, rows correspond to the GTCM competencies. Columns correspond to the Penn State Online courses included in the assessment. Courses that are required for most students are highlighted in light blue. Course authors and instructors were asked to state what students actually do in relation to each of the GTCM competencies. Use the scroll bar at the bottom right edge of the sheet to reveal more courses.
By studying this spreadsheet, you'll gain insight about how individual courses, and how the Penn State Online curriculum as a whole, relate to geospatial workforce needs. If you're interested in comparing ours to curricula at other institutions, ask if they've conducted a similar assessment. If they haven't, ask why not.
Finally, don't forget that you can preview much of our online courseware through our Open Educational Resouces initiative.

13. Distinguishing Properties of Geographic Data
The claim that geographic information science is a distinct field of study implies that spatial data are somehow special data. Goodchild (1992) points out several distinguishing properties of geographic information. I have paraphrased four such properties below. Understanding them, and their implications for the practice of geographic information science, is a key objective of this text.
- Geographic data represent spatial locations and non-spatial attributes measured at certain times.
- Geographic space is continuous.
- Geographic space is nearly spherical.
- Geographic data tend to be spatially dependent.
Let's consider each of these properties next.
14. Locations and Attributes
Geographic data represent spatial locations and non-spatial attributes measured at certain times. Goodchild (1992, p. 33) observes that "a spatial database has dual keys, allowing records to be accessed either by attributes or by locations." Dual keys are not unique to geographic data, but "the spatial key is distinct, as it allows operations to be defined which are not included in standard query languages." In the intervening years, software developers have created variations on SQL that incorporate spatial queries. The dynamic nature of geographic phenomena complicates the issue further, however. The need to pose spatio-temporal queries challenges geographic information scientists (GIScientists) to develop ever more sophisticated ways to represent geographic phenomena, thereby enabling analysts to interrogate their data in ever more sophisticated ways.
15. Continuity
Geographic space is continuous. Although dual keys are not unique to geographic data, one property of the spatial key is. "What distinguishes spatial data is the fact that the spatial key is based on two continuous dimensions" (Goodchild, 1992, p.33). "Continuous" refers to the fact that there are no gaps in the Earth's surface. Canyons, crevasses, and even caverns notwithstanding, there is no position on or near the surface of the Earth that cannot be fixed within some sort of coordinate system grid. Nor is there any theoretical limit to how exactly a position can be specified. Given the precision of modern positioning technologies, the number of unique point positions that could be used to define a geographic entity is practically infinite. Because it's not possible to measure, let alone to store, manage, and process, an infinite amount of data, all geographic data is selective, generalized, approximate. Furthermore, the larger the territory covered by a geographic database, the more generalized the database tends to be.
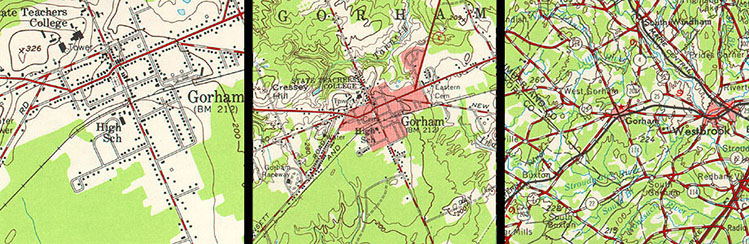
For example, the illustration in Figure 1.16.1, above, shows a town called Gorham depicted on three different topographic maps produced by the United States Geological Survey. Gorham occupies a smaller space on the small-scale (1:250,000) map than it does at 1:62,000 or at 1:24,000. But the relative size of the feature isn't the only thing that changes. Notice that the shape of the feature that represents the town changes also. As does the number of features and the amount of detail shown within the town boundary and in the surrounding area. The name for this characteristically parallel decline in map detail and map scale is generalization.
It is important to realize that generalization occurs not only on printed maps, but in digital databases as well. It is possible to represent phenomena with highly detailed features (whether they be made up of high-resolution raster grid cells or very many point locations) in a single scale-independent database. In practice, however, highly detailed databases are not only extremely expensive to create and maintain, but they also bog down information systems when used in analyses of large areas. For this reason, geographic databases are usually created at several scales, with different levels of detail captured for different intended uses.
16. Nearly Spherical
Geographic space is nearly spherical. The fact that the Earth is nearly, but not quite, a sphere poses some surprisingly complex problems for those who wish to specify locations precisely.

The geographic coordinate system of latitude and longitude coordinates provides a means to define positions on a sphere. Inaccuracies that are unacceptable for some applications creep in, however, when we confront the Earth's "actual" irregular shape, which is called the geoid. Furthermore, the calculations of angles and distance that surveyors and others need to perform routinely are cumbersome with spherical coordinates.
That consideration, along with the need to depict the Earth on flat pieces of paper, compels us to transform the globe into a plane, and to specify locations in plane coordinates instead of spherical coordinates. The set of mathematical transformations by which spherical locations are converted to locations on a plane--called map projections--all lead inevitably to one or another form of inaccuracy.
All this is trouble enough, but we encounter even more difficulties when we seek to define "vertical" positions (elevations) in addition to "horizontal" positions. Perhaps it goes without saying that an elevation is the height of a location above some datum, such as mean sea level. Unfortunately, to be suitable for precise positioning, a datum must correspond closely with the Earth's actual shape. Which brings us back again to the problem of the geoid.
We will consider these issues in greater depth in Chapter 2. For now, suffice it to say that geographic data are unique in having to represent phenomena that are distributed on a continuous and nearly spherical surface.
17. Spatial Dependency
Geographic data tend to be spatially dependent. Spatial dependence is "the propensity for nearby locations to influence each other and to possess similar attributes" (Goodchild, 1992, p.33). In other words, to paraphrase a famous geographer named Waldo Tobler, while everything is related to everything else, things that are close together tend to be more related than things that are far apart. Terrain elevations, soil types, and surface air temperatures, for instance, are more likely to be similar at points two meters apart than at points two kilometers apart. A statistical measure of the similarity of attributes of point locations is called spatial autocorrelation.
Given that geographic data are expensive to create, spatial dependence turns out to be a very useful property. We can sample attributes at a limited number of locations, then estimate the attributes of intermediate locations. The process of estimating unknown values from nearby known values is called interpolation. Interpolated values are reliable only to the extent that the spatial dependence of the phenomenon can be assumed. If we were unable to assume some degree of spatial dependence, it would be impossible to represent continuous geographic phenomena in digital form.
18. Geographic Data and Geographic Questions
The ultimate objective of all geospatial data and technologies, after all, is to produce knowledge. Most of us are interested in data only to the extent that they can be used to help understand the world around us and to make better decisions. Decision-making processes vary a lot from one organization to another. In general, however, the first steps in making a decision are to articulate the questions that need to be answered and to gather and organize the data needed to answer the questions (Nyerges & Golledge, 1997).
Geographic data and information technologies can be very effective in helping to answer certain kinds of questions. The expensive, long-term investments required to build and sustain GIS infrastructures can be justified only if the questions that confront an organization can be stated in terms that GIS is equipped to answer. As a specialist in the field, you may be expected to advise clients and colleagues on the strengths and weaknesses of GIS as a decision support tool. To follow are examples of the kinds of questions that are amenable to GIS analyses, along with questions that GIS is not so well suited to help answer.
Questions concerning individual geographic entities
The simplest geographic questions pertain to individual entities. Such questions include:
Questions about space
- Where is the entity located?
- What is its extent?
Questions about attributes
- What are the attributes of the entity located there?
- Do its attributes match one or more criteria?
Questions about time
- When were the entity's location, extent or attributes measured?
- Has the entity's location, extent, or attributes changed over time?
Simple questions like these can be answered effectively with a good printed map, of course. GIS becomes increasingly attractive as the number of people asking the questions grows, especially if they lack access to the required paper maps.
Questions concerning multiple geographic entities
Harder questions arise when we consider relationships among two or more entities. For instance, we can ask:
Questions about spatial relationships
- Do the entities contain one another?
- Do they overlap?
- Are they connected?
- Are they situated within a certain distance of one another?
- What is the best route from one entity to the others?
- Where are entities with similar attributes located?
Questions about attribute relationships
- Do the entities share attributes that match one or more criteria?
- Are the attributes of one entity influenced by changes in another entity?
Questions about temporal relationships
- Have the entities' locations, extents, or attributes changed over time?
Geographic data and information technologies are very well suited to answering moderately complex questions like these. GIS is most valuable to large organizations that need to answer such questions often.
Questions that GIS is not particularly good at answering
Harder still, however, are explanatory questions--such as why entities are located where they are, why they have the attributes they do, and why they have changed as they have. In addition, organizations are often concerned with predictive questions--such as what will happen at this location if thus-and-so happens at that location? In general, commercial GIS software packages cannot be expected to provide clear-cut answers to explanatory and predictive questions right out of the box. Typically, analysts must turn to specialized statistical packages and simulation routines. Information produced by these analytical tools may then be re-introduced into the GIS database, if necessary. Research and development efforts intended to more tightly couple analytical software with GIS software are underway within the GIScience community. It is important to keep in mind that decision support tools like GIS are no substitutes for human experience, insight, and judgment.
At the outset of the chapter, I suggested that producing information by analyzing data is something like producing energy by burning coal. In both cases, technology is used to realize the potential value of a raw material. Also, in both cases, the production process yields some undesirable by-products. Similarly, in the process of answering certain geographic questions, GIS tends to raise others, such as:
- Given the intrinsic imperfections of the data, how reliable are the results of the GIS analysis?
- Does the information produced through GIS analysis tend to systematically benefit some constituent groups at the expense of others?
- Should the data used to make the decision be made public?
- Does the use of GIS affect the organization's decision-making processes in ways that are beneficial to its management, its employees, and its customers?
As is the case in so many endeavors, the answer to a geographic question usually includes more questions.
Try This!
Can you cite an example of a "hard" question that you and your GIS system have been called upon to address?

19. Summary
It's a truism among specialists in geographic information that the lion's share of the cost of most GIS projects is associated with the development and maintenance of a suitable database. It seems appropriate, therefore, that our first course in geographic information systems should focus upon the properties of geographic data.
I began this first chapter by defining data in a generic sense, as sets of symbols that represent measurements of phenomena. I suggested that data are the raw materials from which information is produced. Information systems, such as database management systems, are technologies that people use to transform data into the information needed to answer questions and to make decisions.
Spatial data are special data. They represent the locations, extents, and attributes of objects and phenomena that make up the Earth's surface at particular times. Geographic data differ from other kinds of data in that they are distributed along a continuous, nearly spherical globe. They also have the unique property that the closer two entities are located, the more likely they are to share similar attributes.
GIS is a special kind of information system that combines the capabilities of database management systems with those of mapping systems. GIS is one object of study of the loosely-knit, multidisciplinary field called Geographic Information Science and Technology. GIS is also a profession--one of several that make up the geospatial industry. As Yogi Berra said, "In theory, there's no difference between theory and practice. In practice there is." In the chapters and projects that follow, we'll investigate the nature of geographic information from both conceptual and practical points of view.

20. Bibliography
Chapter 2: Scales and Transformations
1. Overview
Chapter 1 outlined several of the distinguishing properties of geographic data. One is that geographic data are necessarily generalized, and that generalization tends to vary with scale. A second distinguishing property is that the Earth's complex, nearly-spherical shape complicates efforts to specify exact positions on Earth's surface. This chapter explores implications of these properties by illuminating concepts of scale, Earth geometry, coordinate systems, the "horizontal datums" that define the relationship between coordinate systems and the Earth's shape, and the various methods for transforming coordinate data between 3D and 2D grids, and from one datum to another.
Compared to Chapter 1, Chapter 2 may seem long, technical, and abstract, particularly to those for whom these concepts are new.
Objectives
Students who successfully complete Chapter 2 should be able to:
- demonstrate your ability to specify geospatial locations using geographic coordinates;
- convert geographic coordinates between two different formats;
- explain the concept of a horizontal datum;
- calculate the change in a coordinate location due to a change from one horizontal datum to another;
- estimate the magnitude of "datum shift" associated with the adjustment from NAD 27 to NAD 83;
- recognize the kind of transformation that is appropriate to georegister two or more data sets;
- describe the characteristics of the UTM coordinate system, including its basis in the Transverse Mercator map projection;
- plot UTM coordinates on a map;
- describe the characteristics of the SPC system, including map projection on which it is based;
- convert geographic coordinates to SPC coordinates;
- interpret distortion diagrams to identify geometric properties of the sphere that are preserved by a particular projection; and
- classify projected graticules by projection family.
"Try This!" Activities
Take a minute to complete any of the Try This activities that you encounter throughout the chapter. These are fun, thought-provoking exercises to help you better understand the ideas presented in the chapter.

2. Scale
You hear the word "scale" often when you work around people who produce or use geographic information. If you listen closely, you'll notice that the term has several different meanings, depending on the context in which it is used. You'll hear talk about the scales of geographic phenomena and about the scales at which phenomena are represented on maps and aerial imagery. You may even hear the word used as a verb, as in "scaling a map" or "downscaling." The goal of this section is to help you learn to tell these different meanings apart, and to be able to use concepts of scale to help make sense of geographic data.
Specifically, in this part of Chapter 2 you will learn to:
- calculate map scale using representative fractions;
- describe the general relationship between map scale, detail, and accuracy.
3. Scale as Scope
Often "scale" is used as a synonym for "scope" or "extent." For example, the title of an international research project called The Large Scale Biosphere-Atmosphere Experiment in Amazonia (1999) uses the term "large scale" to describe a comprehensive study of environmental systems operating across a large region. This usage is common not only among environmental scientists and activists, but also among economists, politicians, and the press. Those of us who specialize in geographic information usually use the word "scale" differently, however.
4. Map and Photo Scale
When people who work with maps and aerial images use the word "scale," they usually are talking about the sizes of things that appear on a map or air photo, relative to the actual sizes of those things on the ground.
Map scale is the proportion between a distance on a map and a corresponding distance on the ground:
(Dm / Dg).
By convention, the proportion is expressed as a "representative fraction" in which map distance (Dm) is reduced to 1. The proportion, or ratio, is also typically expressed in the form 1 : Dg rather than 1 / Dg.
The representative fraction 1:100,000, for example, means that a section of road that measures 1 unit in length on a map stands for a section of road on the ground that is 100,000 units long.
If we were to change the scale of the map such that the length of the section of road on the map was reduced to, say, 0.1 units in length, we would have created a smaller-scale map whose representative fraction is 0.1:100,000, or 1:1,000,000. When we talk about large- and small-scale maps and geographic data, then, we are talking about the relative sizes and levels of detail of the features represented in the data. In general, the larger the map scale, the more detail is shown. This tendency is illustrated below in Figure 2.5.1.

One of the defining characteristics of topographic maps is that scale is consistent across each map and within each map series. This isn't true for aerial imagery, however, except for images that have been orthorectified. As discussed in Chapter 6, large scale maps are typically derived from aerial imagery. One of the challenges associated with using air photos as sources of map data is that the scale of an aerial image varies from place to place as a function of the elevation of the terrain shown in the scene. Assuming that the aircraft carrying the camera maintains a constant flying height (which pilots of such aircraft try very hard to do), the distance between the camera and the ground varies along each flight path. This causes air photo scale to be larger where the terrain is higher and smaller where the terrain is lower. An "orthorectified" image is one in which variations in scale caused by variations in terrain elevation (among other effects) have been removed.
You can calculate the average scale of an unrectified air photo by solving the equation Sp = f / (H-havg), where f is the focal length of the camera, H is the flying height of the aircraft above mean sea level, and havg is the average elevation of the terrain. You can also calculate air photo scale at a particular point by solving the equation Sp = f / (H-h), where f is the focal length of the camera, H is the flying height of the aircraft above mean sea level, and h is the elevation of the terrain at a given point.

5. Graphic Map Scales
Another way to express map scale is with a graphic (or "bar") scale. Unlike representative fractions, graphic scales remain true when maps are shrunk or magnified.

If they include a scale at all, most maps include a bar scale like the one shown above left (Figure 2.6.1). Some also express map scale as a representative fraction. Either way, the implication is that scale is uniform across the map. In fact, except for maps that show only very small areas, scale varies across every map. As you probably know, this follows from the fact that positions on the nearly-spherical Earth must be transformed to positions on two-dimensional sheets of paper. Systematic transformations of this kind are called map projections. As we will discuss in greater depth later in this chapter, all map projections are accompanied by deformation of features in some or all areas of the map. This deformation causes map scale to vary across the map. Representative fractions may, therefore, specify map scale along a line at which deformation is minimal (nominal scale). Bar scales denote only the nominal or average map scale. Variable scales, like the one illustrated above right, show how scale varies, in this case by latitude, due to deformation caused by map projection.
6. Map Scale and Accuracy
One of the special characteristics of geographic data is that phenomena shown on maps tend to be represented differently at different scales. Typically, as scale decreases, so too does the number of different features and the detail with which they are represented. Not only printed maps, but also digital geographic data sets that cover extensive areas, tend to be more generalized than datasets that cover limited areas.
Accuracy also tends to vary in proportion with map scale. The United States Geological Survey, for example, guarantees that the mapped positions of 90 percent of well-defined points shown on its topographic map series at scales smaller than 1:20,000 will be within 0.02 inches of their actual positions on the map (see the National Geospatial Program Standards and Specifications). Notice that this "National Map Accuracy Standard" is scale-dependent. The allowable error of well-defined points (such as control points, road intersections, and such) on 1:250,000 scale topographic maps is thus 1 / 250,000 = 0.02 inches / Dg or Dg = 0.02 inches x 250,000 = 5,000 inches or 416.67 feet. Neither small-scale maps nor the digital data derived from them are reliable sources of detailed geographic information.

Sometimes the detail lost on small-scale maps causes serious problems. For example, a contractor hired to use GIS to find a suitable site for a low-level radioactive waste storage facility in Pennsylvania presented a series of 1:1,500,000 scale maps at public hearings around the state in the early 1990s. The scale was chosen so that disqualified areas of the entire state could be printed on a single 11 x 17-inch page. A report accompanying the map included the disclaimer that "it is possible that small areas of sufficient size for the LLRW disposal facility site may exist within regions that appear disqualified on the [map]. The detailed information for these small areas is retained within the GIS even though they are not visually illustrated..." (Chem-Nuclear Systems, Inc. 1993, p. 20). Unfortunately for the contractor, alert citizens recognized the shortcomings of the small-scale map, and newspapers published reports accusing the out-of-state company of providing inaccurate documents. Subsequent maps were produced at a scale large enough to discern 500-acre suitable areas.
7. Scale as a Verb
The term "scale" is sometimes used as a verb. To scale a map is to reproduce it at a different size. For instance, if you photographically reduce a 1:100,000-scale map to 50 percent of its original width and height, the result would be one-quarter the area of the original. Obviously, the map scale of the reduction would be smaller too: 1/2 x 1/100,000 = 1/200,000.
Because of the inaccuracies inherent in all geographic data, particularly in small scale maps, scrupulous geographic information specialists avoid enlarging source maps. To do so is to exaggerate generalizations and errors. The original map used to illustrate areas in Pennsylvania disqualified from consideration for low-level radioactive waste storage shown on an earlier page, for instance, was printed with the statement "Because of map scale and printing considerations, it is not appropriate to enlarge or otherwise enhance the features on this map."

8. Geospatial Measurement Scales
The word "scale" can also be used as a synonym for a ruler--a measurement scale. Because data consist of symbols that represent measurements of phenomena, it's important to understand the reference systems used to take the measurements in the first place. In this section, we'll consider a measurement scale known as the geographic coordinate system that is used to specify positions on the Earth's roughly spherical surface. In other sections, we'll encounter two-dimensional (plane) coordinate systems, as well as the measurement scales used to specify attribute data.
In this section of Chapter 2, you will:
- demonstrate your ability to specify geospatial locations using geographic coordinates;
- convert geographic coordinates between two different formats.
9. Coordinate Systems
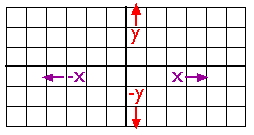
As you probably know, locations on the Earth's surface are measured and represented in terms of coordinates. A coordinate is a set of two or more numbers that specifies the position of a point, line, or other geometric figure in relation to some reference system. The simplest system of this kind is a Cartesian coordinate system (named for the 17th century mathematician and philosopher René Descartes). A Cartesian coordinate system is simply a grid formed by juxtaposing two measurement scales, one horizontal (x) and one vertical (y). The point at which both x and y equal zero is called the origin of the coordinate system. In Figure 2.10.1, above, the origin (0,0) is located at the center of the grid. All other positions are specified relative to the origin. The coordinate of upper right-hand corner of the grid is (6,3). The lower left-hand corner is (-6,-3). If this is not clear, please ask for clarification!
Cartesian and other two-dimensional (plane) coordinate systems are handy due to their simplicity. For obvious reasons, they are not perfectly suited to specifying geospatial positions, however. The geographic coordinate system is designed specifically to define positions on the Earth's roughly-spherical surface. Instead of the two linear measurement scales, x and y, the geographic coordinate systems juxtaposes two curved measurement scales. The east-west scale, called longitude (conventionally designated by the Greek symbol lambda), ranges from +180° to -180°. Because the Earth is round, +180° (or 180° E) and -180° (or 180° W) are the same grid line. That grid line is roughly the International Date Line, which has diversions that pass around some territories and island groups. Opposite the International Date Line is the prime meridian, the line of longitude defined by international treaty as 0°. The north-south scale, called latitude (designated by the Greek symbol phi), ranges from +90° (or 90° N) at the North pole to -90° (or 90° S) at the South pole. We'll take a closer look at the geographic coordinate system next.

10. Geographic Coordinate System

Longitude specifies positions east and west as the angle between the prime meridian and a second meridian that intersects the point of interest. Longitude ranges from +180 (or 180° E) to -180° (or 180° W). 180° East and West longitude together form the International Date Line.
Latitude specifies positions north and south in terms of the angle subtended at the center of the Earth between two imaginary lines, one that intersects the equator and another that intersects the point of interest. Latitude ranges from +90° (or 90° N) at the North pole to -90° (or 90° S) at the South pole. A line of latitude is also known as a parallel.
At higher latitudes, the length of parallels decreases to zero at 90° North and South. Lines of longitude are not parallel but converge toward the poles. Thus, while a degree of longitude at the equator is equal to a distance of about 111 kilometers, that distance decreases to zero at the poles.

11. Geographic Coordinate Formats
Geographic coordinates may be expressed in decimal degrees, or in degrees, minutes, and seconds. Sometimes, you need to convert from one form to another. Steve Kiouttis (personal communication, Spring 2002), manager of the Pennsylvania Urban Search and Rescue Program, described one such situation on the course Bulletin Board: "I happened to be in the state Emergency Operations Center in Harrisburg on Wednesday evening when a call came in from the Air Force Rescue Coordination Center in Dover, DE. They had an emergency locator transmitter (ELT) activation and requested the PA Civil Air Patrol to investigate. The coordinates given to the watch officer were 39 52.5 n and -75 15.5 w. This was plotted incorrectly (treated as if the coordinates were in decimal degrees 39.525n and -75.155 w) and the location appeared to be near Vineland, New Jersey. I realized that it should have been interpreted as 39 degrees 52 minutes and 5 seconds n and -75 degrees and 15 minutes and 5 seconds w) and made the conversion (as we were taught in Chapter 2) and came up with a location on the grounds of Philadelphia International Airport, which is where the locator was found, in a parked airliner."
Here's how it works:
To convert -89.40062 from decimal degrees to degrees, minutes, seconds:
- Subtract the number of whole degrees (89°) from the total (89.40062°). (The minus sign is used in the decimal degree format only to indicate that the value is a west longitude or a south latitude.)
- Multiply the remainder by 60 minutes (.40062 x 60 = 24.0372).
- Subtract the number of whole minutes (24') from the product.
- Multiply the remainder by 60 seconds (.0372 x 60 = 2.232).
- The result, expressed in the correct number of significant figures, is 89° 24' 2.2" W or S.
To convert 43° 4' 31" from degrees, minutes, seconds to decimal degrees:
DD = Degrees + (Minutes/60) + (Seconds/3600)
- Divide the number of seconds by 60 (31 ÷ 60 = 0.5166).
- Add the quotient of step (1) to the whole number of minutes (4 + 0.5166).
- Divide the result of step (2) by 60 (4.5166 ÷ 60 = 0.0753).
- Add the quotient of step (3) to the number of whole number degrees (43 + 0.0753).
- The result, expressed in the correct number of significant figures, is 43.075°

12. Horizontal Datums
Geographic data represent the locations and attributes of things on the Earth's surface. Locations are measured and encoded in terms of geographic coordinates (i.e., latitude and longitude) or plane coordinates (e.g., UTM). To measure and specify coordinates accurately, one first must define the geometry of the surface itself. To see what I mean, imagine a soccer ball. If you or your kids play soccer you can probably conjure up a vision of a round mosaic of 20 hexagonal (six sided) and 12 pentagonal (five sided) panels (soccer balls come in many different designs, but the 32-panel ball is used in most professional matches. Visit Soccer Ball World for more than you ever wanted to know about soccer balls). Now focus on one point at an intersection of three panels. You could use spherical (e.g., geographic) coordinates to specify the position of that point. But if you deflate the ball, the position of the point in space changes, and so must its coordinates. The absolute (though not the relative) position of a point on a surface, then, depends upon the shape of the surface.
Every position is determined in relation to at least one other position. Coordinates, for example, are defined relative to the origin of the coordinate system grid. A land surveyor measures the "corners" of a property boundary relative to a previously-surveyed control point. Surveyors and engineers measure elevations at construction sites and elsewhere. Elevations are expressed in relation to a vertical datum, a reference surface such as mean sea level. As you probably know, there is also such a thing as a horizontal datum, although this is harder to explain and to visualize than the vertical case. Horizontal datums define the geometric relationship between a coordinate system grid and the Earth's surface. Because the Earth's shape is complex, the relationship is too. The goal of this section is to explain the relationship.
Specifically, in this section of Chapter 2 you will learn to:
- explain the concept of a horizontal datum;
- calculate the change in a coordinate location due to a change from one horizontal datum to another;
- estimate the magnitude of "datum shift" associated with the adjustment from NAD 27 to NAD 83.
13. Geoids

The accuracy of coordinates that specify geographic locations depends upon how the coordinate system grid is aligned with the Earth's surface. Unfortunately for those who need accurate geographic data, defining the shape of the Earth's surface is a non-trivial problem. So complex is the problem that an entire profession, called geodesy, has arisen to deal with it.
Geodesists define the Earth's surface as a surface that closely approximates global mean sea level, but across which gravity is everywhere equal. They refer to this shape as the geoid. Geoids are lumpy because gravity varies from place to place in response to local differences in terrain and variations in the density of materials in the Earth's interior. Geoids are also a little squat. Sea level gravity at the poles is greater than sea level gravity at the equator, a consequence of Earth's "oblate" shape as well as the centrifugal force associated with its rotation.
Geodesists at the U.S. National Geodetic Survey describe the geoid as an "equipotential surface" because the potential energy associated with the Earth's gravitational pull is equivalent everywhere on the surface. Like fitting a trend line through a cluster of data points, the geoid is a three-dimensional statistical surface that fits as closely as possible gravity measurements taken at millions of locations around the world. As additional and more accurate gravity measurements become available, geodesists revise the geoid periodically. Some geoid models are solved only for limited areas; GEOID03, for instance, is calculated only for the continental U.S.
Recall that horizontal datums define how coordinate system grids align with the Earth's surface. Long before geodesists calculated geoids, surveyors used much simpler surrogates called ellipsoids to model the shape of the Earth.
14. Ellipsoids

An ellipsoid is a three-dimensional geometric figure that resembles a sphere, but whose equatorial axis (a in Figure 2.15.1, above) is slightly longer than its polar axis (b). The equatorial axis of the World Geodetic System of 1984, for instance, is approximately 22 kilometers longer than the polar axis, a proportion that closely resembles the oblate spheroid that is planet Earth. Ellipsoids are commonly used as surrogates for geoids so as to simplify the mathematics involved in relating a coordinate system grid with a model of the Earth's shape. Ellipsoids are good, but not perfect, approximations of geoids. The map in Figure 2.15.2, below shows differences in elevation between a geoid model called GEOID96 and the WGS84 ellipsoid. The surface of GEOID96 rises up to 75 meters above the WGS84 ellipsoid over New Guinea (where the map is colored red). In the Indian Ocean (where the map is colored purple), the surface of GEOID96 falls about 104 meters below the ellipsoid surface.

Many ellipsoids are in use around the world. (Wikipedia presents a list in its entry on Earth Ellipsoids) Local ellipsoids minimize differences between the geoid and the ellipsoid for individual countries or continents. The Clarke 1866 ellipsoid, for example, minimizes deviations in North America. The North American Datum of 1927 (NAD 27) associates the geographic coordinate grid with the Clarke 1866 ellipsoid. NAD 27 involved an adjustment of the latitude and longitude coordinates of some 25,000 geodetic control point locations across the U.S. The nationwide adjustment commenced from an initial control point at Meades Ranch, Kansas, and was meant to reconcile discrepancies among the many local and regional control surveys that preceded it.
The North American Datum of 1983 (NAD 83) involved another nationwide adjustment, necessitated in part by the adoption of a new ellipsoid, called GRS 80. Unlike Clarke 1866, GRS 80 is a global ellipsoid centered upon the Earth's center of mass. GRS 80 is essentially equivalent to WGS 84, the global ellipsoid upon which the Global Positioning System is based. NAD 27 and NAD 83 both align coordinate system grids with ellipsoids. They differ simply in that they refer to different ellipsoids. Because Clarke 1866 and GRS 80 differ slightly in shape as well as in the positions of their center points, the adjustment from NAD 27 to NAD 83 involved a shift in the geographic coordinate grid. Because a variety of datums remain in use, geospatial professionals need to understand this shift, as well as how to transform data between horizontal datums.
The preceding statement remains true despite the fact that NAD 83 will soon be discontinued as part of the National Geodetic Survey's ongoing modernization of the U.S. National Spatial Reference System. The switch from a "passive" ellipsoid-based reference system to a GPS-based dynamic system was planned for 2022, but it has since been delayed until 2024 or -25. Visit the National Geodetic Survey for the latest information.
15. Control Points and Datum Shifts

Geoids, ellipsoids, and even coordinate systems are all abstractions. The fact that "horizontal datum" refers to a relationship between an ellipsoid and a coordinate system, two abstractions, may explain why the concept is so frequently misunderstood. Datums do have physical manifestations, however.
Shown above (Figure 2.16.1) is one of the approximately two million horizontal and vertical control points that have been established in the U.S. Although control point markers are fixed, the coordinates that specify their locations are liable to change. The U.S. National Geodetic Survey maintains a database of the coordinate specifications of these control points, including historical locations as well as more recent adjustments. One occasion for adjusting control point coordinates is when new horizontal datums are adopted. Since every coordinate system grid is aligned with an ellipsoid that approximates the Earth's shape, coordinate grids necessarily shift when one ellipsoid is replaced by another. When coordinate system grids shift, the coordinates associated with fixed control points need to be adjusted. How we account for the Earth's shape makes a difference in how we specify locations.
Try This!
Here's a chance to calculate how much the coordinates of a control point change in response to an adjustment from North American Datum of 1927 (based on the Clarke 1866 ellipsoid) to the North American Datum of 1983 (based upon the GRS 80 ellipsoid).
- Find the geographic coordinates of a populated place
- Start at the USGS' Geographic Names Information System at the U.S. Board on Geographic Names.
- Follow the links labeled Domestic Names, then Search to search place names included in the Geographic Names Information System.
- At the Query Form, enter the name of your home town (or other named geographic feature) in the Feature Name field, as well as your home State. Choose Populated Place (or other, as appropriate) for the Feature Class.
- If your home is somewhere other than the U.S., enter a place name of interest or fantasy destination (e.g., "Las Vegas" ;-) ).
- Click Send Query.
- The result should include latitude and longitude coordinates of a centroid that represents where the name your town (or other feature) would appear on a map. You'll need those coordinates for the next step.
- Find the geographic coordinates of a nearby horizontal control point
- Visit the U.S. National Geodetic Survey home page.
- Follow the link labeled Survey Mark Datasheets.
- At the NGS Datasheet page, follow the link labeled Datasheets.
- You may wish to begin with the "Info Link" labeled "Tell me more about datasheets."
- At the NGS Datasheet Retrieval page, follow the link labeled Radial Search. (You're welcome to experiment with another retrieval method if you wish.)
- At the NGS Datasheet Point Radius form:
- Enter the latitude and longitude coordinates you looked up in step #1. Pay attention to the input format.
- Specify a Search Radius.
- Select Any Horz. and/or Vert. Control from the Data Type Desired scrolling field.
- Select Any Stability from the Stability Desired scrolling field.
- Click Submit.
- The result should be a Station List Results form that looks like the contents of the window pictured below. These are the results of my search on the centroid coordinates for State College PA. Note that I have highlighted the station that is both nearest to the coordinates I entered and a first-order control point (see the "1" under the column labeled "H"?)
 Figure 2.16.2 Station List ResultsCredit: noaa.gov
Figure 2.16.2 Station List ResultsCredit: noaa.gov - Select the station nearest to the coordinates you specified that is also the highest-order horizontal control point.
- Click Get Datasheets. The system should respond with a station datasheet like this example.
- In the example linked above, the CURRENT SURVEY CONTROL of the station point is listed as NAD 83(1992) 40 48 13.83840(N) 077 51 44.25410(W) ADJUSTED. These are the geographic coordinates of the control point relative to the NAD 83 horizontal datum. In the next step, we'll see how much the control point "moved" as a result of the adjustment of those coordinates from the earlier NAD 27 datum. (The geographic coordinates of the control point are specified to 100,000th of a second precision, or approximately 0.3 mm of longitude. Keep in mind, however, the difference between precision and accuracy; the trailing 0 suggests that the accuracy is an order of magnitude less than the precision.)
- Calculate the datum shift associated with a conversion from one horizontal datum to another
- Return to the U.S. National Geodetic Survey home page.
- Follow the link labeled geodetic tool kit.
- At the NGS Geodetic Tool Kit page, follow the link labeled NADCON (you'll be taken to an explanatory page, where you'll need to click NADCON again to proceed to the utility).
- At the North American Datum Conversion Utility page, read the introductory paragraphs.
- At the NADCON computations form, under the heading compute a datum shift for a specific location:
- Select direction of conversion: NAD 83 to NAD27.
- Enter the NAD 83 latitude and longitude coordinates of your control station. Pay attention to format.
- Click Compute Datum Shift for a Single Location.
- The result should be a NADCON Output report like this example. In the State College example, the adjustment from NAD 83 to NAD 27 (associated with the replacement of the old Clarke 1866 ellipsoid by the Earth-centered GRS 80 ellipsoid) caused the geographic coordinate system grid to shift nearly 7 meters South and over 23 meters West. That grid shift is reflected in the adjustment of the coordinates that specify the control point's location. Note that the point didn't move, rather, the grid shifted. How much shift occurred at your location?

16. Coordinate Transformations
GIS specialists often need to transform data from one coordinate system and/or datum to another. For example, digital data produced by tracing paper maps over a digitizing tablet need to be transformed from the tablet's non-georeferenced plane coordinate system into a georeferenced plane or spherical coordinate system that can be georegistered with other digital data "layers." Raw image data produced by scanning the Earth's surface from space tend to be skewed geometrically as a result of satellite orbits and other factors; to be useful these too need to be transformed into georeferenced coordinate systems. Even the point data produced by GPS receivers, which are measured as latitude and longitude coordinates based upon the WGS84 datum, often need to be transformed to other coordinate systems or datums to match project specifications. This section describes three categories of coordinate transformations: (1) plane coordinate transformations; (2) datum transformations; and (3) map projections.
Students who successfully complete this section of Chapter 2 should be able to:
recognize the kind of transformation that is appropriate to georegister two or more data sets.
17. Plane Coordinate Transformations
Some coordinate transformations are simple. For example, the transformation from non-georeferenced plane coordinates to non-georeferenced polar coordinates shown in Figure 2.18.1, below, involves nothing more than the replacement of one kind of coordinates with another.
Unfortunately, most plane coordinate transformation problems are not so simple. The geometries of non-georeferenced plane coordinate systems and georeferenced plane coordinate systems tend to be quite different, mainly because georeferenced plane coordinate systems are often projected. As you know, the act of projecting a nearly-spherical surface onto a two-dimensional plane necessarily distorts the geometry of the original spherical surface. Specifically, the scale of a projected map (or an unrectified aerial photograph, for that matter) varies from place to place. So long as the geographic area of interest is not too large, however, formulae like the ones described here can be effective in transforming a non-georeferenced plane coordinate system grid to match a georeferenced plane coordinate system grid with reasonable, and measurable, accuracy. We won't go into the math of the transformations here, since the formulae are implemented within GIS software. Instead, this section aims to familiarize you with how some common transformations work and how they may be used.
Similarity Transformation
In the hypothetical illustration below (Figure 2.18.2), the spatial arrangement of six control points digitized from a paper map ("before") are shown to differ from the spatial arrangement of the same points that appear in a georeferenced aerial photograph that is referenced to a different plane coordinate system grid ("after"). If, as shown, the arrangement of the two sets of points differs only in scale, rotation, and offset, a relatively simple four-parameter similarity transformation may do the trick. Your GIS software should derive the parameters for you by comparing the relative positions of the common points. Note that while only six control points are illustrated, ten to twenty control points are recommended (Chrisman 2002).
Affine Transformation
Sometimes a similarity transformation doesn't do the trick. For example, because paper maps expand and contract more along the paper grain than across the grain in response to changes in humidity, the scale of a paper map is likely to be slightly greater along one axis than the other. In such cases, a six-parameter affine transformation may be used to accommodate differences in scale, rotation, and offset along each of the two dimensions of the source and target coordinate systems. This characteristic is particularly useful for transforming image data scanned from polar-orbiting satellites whose orbits trace S-shaped paths over the rotating Earth.
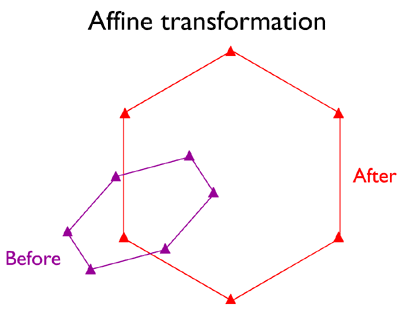
Second-Order Polynomial Transformation
When neither similarity nor affine transformations yield acceptable results, you may have to resort to a twelve-parameter Second-order polynomial transformation. Their advantage is the potential to correct data sets that are distorted in several ways at once. A disadvantage is that the stability of the results depend very much upon the quantity and arrangement of control points and the degree of dissimilarity of the source and target geometries (Iliffe 2000).
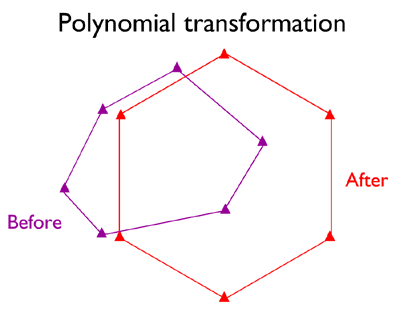
Even more elaborate plane transformation methods, known collectively as rubber sheeting, optimize the fit of a source data set to the geometry of a target data set as if the source data were mapped onto a stretchable sheet.
Root Mean Square Error
GIS software provides a statistical measure of how well a set of transformed control points match the positions of the same points in a target data set. Put simply, Root Mean Square (RMS) Error is the average of the distances (also known as residuals) between each pair of control points. What constitutes an acceptably low RMS Error depends on the nature of the project and the scale of analysis.

18. Datum Transformations
Point locations are specified in terms of (a) their positions relative to some coordinate system grid and (b) their heights above or below some reference surface. Obviously, the elevation of a stationary point depends upon the size and shape of the reference surface (e.g., mean sea level) upon which the elevation measurement is based. In the same way, a point's position in a coordinate system grid depends on the size and shape of the surface upon which the grid is draped. The relationship between a grid and a model of the Earth's surface is called a horizontal datum. GIS specialists who are called upon to merge data sets produced at different times and in different parts of the world need to be knowledgeable about datum transformations.
NAD 27 to NAD 83
In the U.S., the two most frequently encountered horizontal datums are the North American Datum of 1927 (NAD 27) and the North American Datum of 1983 (NAD 83). The advent of the Global Positioning System necessitated an update of NAD 27 that included (a) adoption of a geocentric ellipsoid, GRS 80, in place of the Clarke 1866 ellipsoid; and (b) correction of many distortions that had accrued in the older datum. Bearing in mind that the realization of a datum is a network of fixed control point locations that have been specified in relation to the same reference surface, the 1983 adjustment of the North American Datum caused the coordinate values of every control point managed by the National Geodetic Survey (NGS) to change. Obviously, the points themselves did not shift on account of the datum transformation (although they did move a centimeter or more a year due to plate tectonics). Rather, the coordinate system grids based upon the datum shifted in relation to the new ellipsoid. And because local distortions were adjusted at the same time, the magnitude of grid shift varies from place to place. The illustrations below compare the magnitude of the grid shifts associated with the NAD 83 adjustment at one location and nationwide.


Given the irregularity of the shift, NGS could not suggest a simple transformation algorithm that surveyors and mappers could use to adjust local data based upon the older datum. Instead, NGS created a software program called NADCON (Dewhurst 1990, Mulcare 2004) that calculates adjusted coordinates from user-specified input coordinates by interpolation from a pair of 15° correction grids generated by NGS from hundreds of thousands of previously-adjusted control points.
GPS Data and WGS 84
The U.S. Department of Defense created the Global Positioning System (GPS) over a period of 16 years at a startup cost of about $10 billion. GPS receivers calculate their positions in terms of latitude, longitude, and height above or below the World Geodetic System of 1984 ellipsoid (WGS 84). Developed specifically for the Global Position System, WGS 84 is an Earth-centered ellipsoid which, unlike the many regional, national, and local ellipsoids still in use, minimizes deviations from the geoid worldwide. Depending on where a GIS specialist may be working, or what data he or she may need to work with, the need to transform GPS data from WGS 84 to some other datum is likely to arise. Datum transformation algorithms are implemented within GIS software as well as in the post-processing software provided by GPS vendors for use with their receivers. Some transformation algorithms yield more accurate results than others. The method you choose will depend on what choices are available to you and how much accuracy your application requires.
Unlike the plane transformations described earlier, datum transformations involve ellipsoids and are therefore three-dimensional. The simplest is the three-parameter Molodenski transformation. In addition to knowledge of the size and shape of the source and target ellipsoids (specified in terms of semimajor axis, the distance from the ellipsoid's equator to its center, and flattening ratio, the degree to which the ellipsoid is flattened to approximate the Earth's oblate shape), the offset between the two ellipsoids needs to be specified along X, Y, and Z axes. The window shown below (Figure 2.19.3) illustrates ellipsoidal and offset parameters for several horizontal datums, all expressed in relation to WGS 84.

For larger study areas, more accurate results may be obtained using a seven-parameter transformation that accounts for rotation as well as scaling and offset.
Finally, surface-fitting transformations like the NADCON grid interpolation described above yield the best results over the largest areas.
For routine mapping applications covering relatively small geographic areas (i.e., larger than 1:25,000), the plane transformations described earlier may yield adequate results when datum specifications are unknown and when a sufficient number of appropriately distributed control points can be identified.

19. Map Projections
Latitude and longitude coordinates specify positions in a more-or-less spherical grid called the graticule. Plane coordinates like the eastings and northings in the Universal Transverse Mercator (UTM) and State Plane Coordinates (SPC) systems denote positions in flattened grids. This is why georeferenced plane coordinates are referred to as projected, and geographic coordinates are called unprojected. The mathematical equations used to transform latitude and longitude coordinates to plane coordinates are called map projections. Inverse projection formulae transform plane coordinates to geographic. The simplest kind of projection, illustrated in Figure 2.20.1, below, transforms the graticule into a rectangular grid in which all grid lines are straight, intersect at right angles, and are equally spaced. More complex projections yield grids in which the lengths, shapes, and spacing of the grid lines vary.

If you are a GIS practitioner, you have probably faced the need to superimpose unprojected latitude and longitude data onto projected data, and vice versa. For instance, you might have needed to merge geographic coordinates measured with a GPS receiver with digital data published by the USGS that are encoded as UTM coordinates. Modern GIS software provides sophisticated tools for projecting and unprojecting data. To use such tools most effectively, you need to understand the projection characteristics of the data sets you intend to merge. We'll examine map projections in some detail elsewhere in this chapter. Here, let's simply review the characteristics that are included in the "Spatial Reference Information" section of the metadata documents that (ideally!) accompany the data sets you might wish to incorporate in your GIS. These include:
- Projection Name Most common in the GIS realm is the Transverse Mercator, which serves as the basis of the global UTM plane coordinate system, the U.K. and proposed U.S. National Grids, and many zones in the U.S. State Plane Coordinate system (SPC). Other SPC zones are based upon the Lambert Conic Conformal projection, which like many projections is named for its inventor as well as its projection category (conic) and the geometric properties it preserves (conformal). Much map data, particularly in the form of printed paper maps, are based upon "legacy" projections (like the Polyconic in the U.S.) that are no longer widely used. A much greater variety of projection types tend to be used in small scale thematic mapping than in large scale reference mapping.
- Central Meridian Although no land masses are shown, let's assume that the graticule and projected grid shown above are centered on the intersection of the equator (0 latitude) and prime meridian (0° longitude). Most map projection formulae include a parameter that allows you to center the projected map upon any longitude.
- Latitude of Projection Origin Under certain conditions, most map projection formulae allows you to specify different aspects of the grid. Instead of the equatorial aspect illustrated above, you might specify a polar aspect or oblique aspect by varying the latitude of projection origin such that one of the poles, or any latitude between the pole and the equator, is centered in the projected map. As you might imagine, the appearance of the grid changes a lot when viewed at different aspects.
- Scale Factor at Central Meridian This is the ratio of map scale along the central meridian and the scale at a standard meridian, where scale distortion is zero. The scale factor at the central meridian is .9996 in each of the 60 UTM coordinate system zones since each contains two standard lines 180 kilometers west and east of the central meridian. Scale distortion increases with distance from standard lines in all projected coordinate systems.
- Standard Lines Some projections, including the Lambert Conic Conformal, include parameters by which you can specify one or two standard lines along which there is no scale distortion caused by the act of transforming the spherical grid into a flat grid. By the same reasoning that two standard lines are placed in each UTM zone to minimize distortion throughout the zone to a maximum of one part in 1000, two standard parallels are placed in each SPC zone that is based on a Lambert projection such that scale distortion is no worse than one part in 10,000 anywhere in the zone.

20. UTM Coordinate System
Shown below in Figure 2.21.1 is the southwest corner of a 1:24,000-scale topographic map published by the United States Geological Survey (USGS). Note that the geographic coordinates (40 45' N latitude, 77° 52' 30" W longitude) of the corner are specified. Also shown, however, are ticks and labels representing two plane coordinate systems, the Universal Transverse Mercator (UTM) system and the State Plane Coordinates (SPC) system. The tick labeled "4515" represents a UTM grid line (called a "northing") that runs parallel to and 4,515,000 meters north of, the equator. Ticks labeled "258" and "259" represent grid lines that run perpendicular to the equator and 258,000 meters and 259,000 meters east, respectively, of the origin of the UTM Zone 18 North grid. Unlike longitude lines, UTM "eastings" are straight and do not converge upon the Earth's poles. All of this begs the question, Why are multiple coordinate system grids shown on the map? Why aren't geographic coordinates sufficient?

You can think of a plane coordinate system as the juxtaposition of two measurement scales. In other words, if you were to place two rulers at right angles, such that the "0" marks of the rulers aligned, you'd define a plane coordinate system. The rulers are called "axes." The absolute location of any point in the space in the plane coordinate system is defined in terms of distance measurements along the x (east-west) and y (north-south) axes. A position defined by the coordinates (1,1) is located one unit to the right, and one unit up from the origin (0,0). The UTM grid is a widely-used type of geospatial plane coordinate system in which positions are specified as eastings (distances, in meters, east of an origin) and northings (distances north of the origin).
By contrast, the geographic coordinate system grid of latitudes and longitudes consists of two curved measurement scales to fit the nearly-spherical shape of the Earth. As you know, geographic coordinates are specified in degrees, minutes, and seconds of arc. Curved grids are inconvenient to use for plotting positions on flat maps. Furthermore, calculating distances, directions and areas with spherical coordinates are cumbersome in comparison with plane coordinates. For these reasons, cartographers and military officials in Europe and the U.S. developed the UTM coordinate system. UTM grids are now standard not only on printed topographic maps but also for the geospatial referencing of the digital data that comprise the emerging U.S. "National Map."
In this section of Chapter 2, you will learn to:
- describe the characteristics of the UTM coordinate system, including its basis in the Transverse Mercator map projection; and
- plot UTM coordinates on a map.
21. The UTM Grid and Transverse Mercator Projection
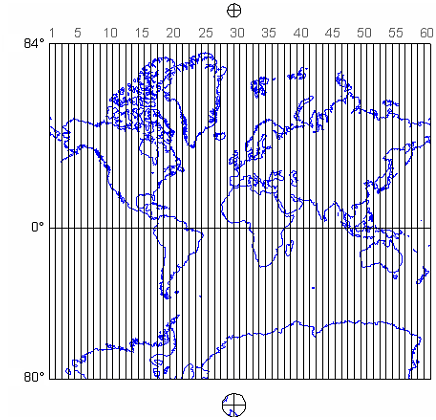
The Universal Transverse Mercator system is not really universal, but it does cover nearly the entire Earth surface. Only polar areas--latitudes higher than 84° North and 80° South--are excluded. (Polar coordinate systems are used to specify positions beyond these latitudes.) The UTM system divides the remainder of the Earth's surface into 60 zones, each spanning 6° of longitude. These are numbered west to east from 1 to 60, starting at 180° West longitude (roughly coincident with the International Date Line).
The illustration above (Figure 2.22.1) depicts UTM zones as if they were uniformly "wide" from the Equator to their northern and southern limits. In fact, since meridians converge toward the poles on the globe, every UTM zone tapers from 666,000 meters in "width" at the Equator (where 1° of longitude is about 111 kilometers in length) to only about 70,000 meters at 84° North and about 116,000 meters at 80° South.
"Transverse Mercator" refers to the manner in which geographic coordinates are transformed into plane coordinates. Such transformations are called map projections. The illustration below (Figure 2.22.2) shows the 60 UTM zones as they appear when projected using a Transverse Mercator map projection formula that is optimized for the UTM zone highlighted in yellow, Zone 30, which spans 6° West to 0° East longitude (the prime meridian).
As you can imagine, you can't flatten a globe without breaking or tearing it somehow. Similarly, the act of mathematically transforming geographic coordinates to plane coordinates necessarily displaces most (but not all) of the transformed coordinates to some extent. Because of this, map scale varies within projected (plane) UTM coordinate system grids.
The distortion ellipses plotted in red help us visualize the pattern of scale distortion associated with a particular projection. Had no distortion occurred in the process of projecting the map shown in Figure 2.22.2, below, all of the ellipses would be the same size, and circular in shape. As you can see, the ellipses centered within the highlighted UTM zone are all the same size and shape. Away from the highlighted zone, the ellipses steadily increase in size, although their shapes remain uniformly circular. This pattern indicates that scale distortion is minimal within Zone 30, and that map scale increases away from that zone. Furthermore, the ellipses reveal that the character of distortion associated with this projection is that shapes of features as they appear on a globe are preserved while their relative sizes are distorted. Map projections that preserve shape by sacrificing the fidelity of sizes are called conformal projections. The plane coordinate systems used most widely in the U.S., UTM and SPC (the State Plane Coordinates system) are both based upon conformal projections.

The Transverse Mercator projection illustrated above (Figure 2.22.2) minimizes distortion within UTM zone 30. Fifty-nine variations on this projection are used to minimize distortion in the other 59 UTM zones. In every case, distortion is no greater than 1 part in 1,000. This means that a 1,000 meter distance measured anywhere within a UTM zone will be no worse than + or - 1 meter off.
The animation linked to the illustration in Figure 2.22.3, below, shows a series of 60 Transverse Mercator projections that form the 60 zones of the UTM system. Each zone is based upon a unique Transverse Mercator map projection that minimizes distortion within that zone. Zones are numbered 1 to 60 eastward from the international date line. The animation begins with Zone 1.

Try This!
Click the graphic above in Figure 2.22.3 to download and view the animation file (utm.mp4) in a new tab.
Map projections are mathematical formulae used to transform geographic coordinates into plane coordinates. (Inverse projection formulae transform plane coordinates back into latitudes and longitudes.) "Transverse Mercator" is one of a hypothetically infinite number of such projection formulae. A visual analog to the Transverse Mercator projection appears below in Figure 2.22.4. Conceptually, the Transverse Mercator projection transfers positions on the globe to corresponding positions on a cylindrical surface, which is subsequently cut from end to end and flattened. In the illustration, the cylinder is tangent to the globe along one line, called the standard line. As shown in the little world map beside the globe and cylinder, scale distortion is minimal along the standard line and increases with distance from it. The animation linked above (Figure 2.22.3) was produced by rotating the cylinder 59 times at an increment of 6°.

In the illustration above in Figure 2.22.4, there is one standard meridian. Some projection formulae, including the Transverse Mercator projection, allow two standard lines. Each of the 60 variations on the Transverse Mercator projection used as the foundations of the 60 UTM zones employ not one, but two, standard lines. These two standard lines are parallel to, and 180,000 meters east and west of, each central meridian. This scheme ensures that the maximum error associated with the projection due to scale distortion will be 1 part in 1,000 (at the outer edge of the zone at the equator). The error due to scale distortion at the central meridian is 1 part in 2,500. Distortion is zero, of course, along the standard lines.
So, what does the term "transverse" mean? This simply refers to the fact that the cylinder shown above in Figure 2.22.4 has been rotated 90° from the equatorial aspect of the standard Mercator projection, in which a single standard line coincides with 0° latitude.

One disadvantage of the UTM system is that multiple coordinate systems must be used to account for large entities. The lower 48 United States, for instance, spread across ten UTM zones. The fact that there are many narrow UTM zones can lead to confusion. For example, the city of Philadelphia, Pennsylvania is east of the city of Pittsburgh. If you compare the Eastings of centroids representing the two cities, however, Philadelphia's Easting (about 486,000 meters) is less than Pittsburgh's (about 586,000 meters). Why? Because although the cities are both located in the U.S. state of Pennsylvania, they are situated in two different UTM zones. As it happens, Philadelphia is closer to the origin of its Zone 18 than Pittsburgh is to the origin of its Zone 17. If you were to plot the points representing the two cities on a map, ignoring the fact that the two zones are two distinct coordinate systems, Philadelphia would appear to the west of Pittsburgh. Inexperienced GIS users make this mistake all the time. Fortunately, GIS software is getting sophisticated enough to recognize and merge different coordinate systems automatically.

22. UTM Zone Characteristics
The illustration in Figure 2.23.1, below, depicts the area covered by a single UTM coordinate system grid zone. Each UTM zone spans 6° of longitude, from 84° North and 80° South. Zones taper from 666,000 meters in "width" at the Equator (where 1° of longitude is about 111 kilometers in length) to only about 70,000 meters at 84° North and about 116,000 meters at 80° South. Polar areas are covered by polar coordinate systems. Each UTM zone is subdivided along the equator into two halves, north and south.

The illustration below in Figure 2.23.2 shows how UTM coordinate grids relate to the area of coverage illustrated above in Figure 2.23.1. The north and south halves are shown side by side for comparison. Each half is assigned its own origin. The north south zone origins are positioned to south and west of the zone. North zone origins are positioned on the Equator, 500,000 meters west of the central meridian. Origins are positioned so that every coordinate value within every zone is a positive number. This minimizes the chance of errors in distance and area calculations. By definition, both origins are located 500,000 meters west of the central meridian of the zone (in other words, the easting of the central meridian is always 500,000 meters E). These are considered "false" origins since they are located outside the zones to which they refer. UTM eastings range from 167,000 meters to 833,000 meters at the equator. These ranges narrow toward the poles. Northings range from 0 meters to nearly 9,400,000 in North zones and from just over 1,000,000 meters to 10,000,000 meters in South zones. Note that positions at latitudes higher than 84° North and 80° South are defined in Polar Stereographic coordinate systems that supplement the UTM system.

See the Bibliography (last page of the chapter) for further readings about the UTM grid system.

23. National Grids
The Transverse Mercator projection provides a basis for existing and proposed national grid systems in the United Kingdom and the United States.
In the U.K., topographic maps published by the Ordnance Survey refer to a national grid of 100 km squares, each of which is identified by a two-letter code. Positions within each grid square are specified in terms of eastings and northings between 0 and 100,000 meters. The U.K. national grid is a plane coordinate system that is based upon a Transverse Mercator projection whose central meridian is 2 West longitude, with standard meridians 180 km west and east of the central meridian. The grid is typically related to the Airy 1830 ellipsoid, a relationship known as the National Grid (OSGB36®) datum. The corresponding UTM zones are 29 (central meridian 9° West) and 30 (central meridian 3° West). One of the advantages of the U.K. national grid over the global UTM coordinate system is that it eliminates the boundary between the two UTM zones.
A similar system has been proposed for the U.S. by the Federal Geographic Data Committee. The proposed "U.S. National Grid" is the same as the Military Grid Reference System (MGRS), a worldwide grid that is very similar to the UTM system. As Phil and Julianna Muehrcke (1998, p.p. 229-230) write in the 4th edition of Map Use, "the military [specifically, the U.S. Department of Defense] aimed to minimize confusion when using long numerical [UTM] coordinates" by specifying UTM zones and sub-zones with letters instead of numbers. Like the UTM system, the MGRS consists of 60 zones, each spanning 6° longitude. Each UTM zone is subdivided into 19 MGRS quadrangles of 8° latitude and one (quadrangle from 72° to 84° North) of 12° latitude. The letters C through X are used to designate the grid cell rows from south to north. I and O are omitted to avoid confusion with numbers. Wikipedia offers a good entry on the MGRS here.
Try This!
Fun Demo of U.K. National Grid
A kids-friendly information sheet about the U.K. National Grid is published by the U.K. Ordnance Survey. You can find it in the National Grid for Schools link on their website.
A less-kids-friendly video can be seen below:

24. State Plane Coordinate System
Shown below in Figure 2.25.1 is the southwest corner of a 1:24,000-scale topographic map published by the United States Geological Survey (USGS). Note that the geographic coordinates (40 45' N latitude, 77° 52' 30" W longitude) of the corner are specified. Also shown, however, are ticks and labels representing two plane coordinate systems, the Universal Transverse Mercator (UTM) system and the State Plane Coordinate (SPC) system. The tick labeled "1 970 000 FEET" represents a SPC grid line that runs perpendicular to the equator and 1,970,000 feet east of the origin of the Pennsylvania North zone. The origin lies far to the west of this map sheet. Other SPC grid lines, called "northings" (not shown in the illustration), run parallel to the equator and perpendicular to SPC eastings at increments of 10,000 feet. Unlike longitude lines, SPC eastings and northings are straight and do not converge upon the Earth's poles.

The SPC grid is a widely-used type of geospatial plane coordinate system in which positions are specified as eastings (distances east of an origin) and northings (distances north of an origin). You can tell that the SPC grid referred to in the map illustrated above is the older 1927 version of the SPC grid system because (a) eastings and northings are specified in feet and (b) grids are based upon the North American Datum of 1927 (NAD27). The 124 zones that make up the State Plane Coordinates system of 1983 are based upon NAD 83, and generally use the metric system to specify eastings and northings.
State Plane Coordinates are frequently used to georeference large scale (small area) surveying and mapping projects because plane coordinates are easier to use than latitudes and longitudes for calculating distances and areas. And because SPC zones extend over relatively smaller areas, less error accrues to positions, distances, and areas calculated with State Plane Coordinates than with UTM coordinates.
In this section you will learn to:
- describe the characteristics of the SPC system, including map projection on which it is based; and
- convert geographic coordinates to SPC coordinates.
25. The SPC Grid and Map Projections
Plane coordinate systems pretend the world is flat. Obviously, if you flatten the entire globe to a plane surface, the sizes and shapes of the land masses will be distorted, as will distances and directions between most points. If your area of interest is small enough, however, and if you flatten it cleverly, you can get away with a minimum of distortion. The basic design problem that confronted the geodesists who designed the State Plane Coordinate System, then, was to establish coordinate system zones that were small enough to minimize distortion to an acceptable level, but large enough to be useful.
The State Plane Coordinate System of 1983 (SPC) is made up of 124 zones that cover the 50 U.S. states. As shown below in Figure 2.26.1, some states are covered with a single zone while others are divided into multiple zones. Each zone is based upon a unique map projection that minimizes distortion in that zone to 1 part in 10,000 or better. In other words, a distance measurement of 10,000 meters will be at worst one meter off (not including instrument error, human error, etc.). The error rate varies across each zone, from zero along the projection's standard lines to the maximum at points farthest from the standard lines. Errors will accrue at a rate much lower than the maximum at most locations within a given SPC zone. SPC zones achieve better accuracy than UTM zones because they cover smaller areas, and so are less susceptible to projection-related distortion.

Most SPC zones are based on either a Transverse Mercator or Lambert Conic Conformal map projection whose parameters (such as standard line(s) and central meridians) are optimized for each particular zone. "Tall" zones like those in New York state, Illinois, and Idaho are based upon unique Transverse Mercator projections that minimize distortion by running two standard lines north-south on either side of the central meridian of each zone. "Wide" zones like those in Pennsylvania, Kansas, and California are based on unique Lambert Conformal Conic projections that run two standard parallels west-east through each zone. (One of Alaska's zones is based upon an "oblique" variant of the Mercator projection. That means that instead of standard lines parallel to a central meridian, as in the transverse case, the Oblique Mercator runs two standard lines that are tilted so as to minimize distortion along the Alaskan panhandle.)
The two types of map projections share the property of conformality, which means that angles plotted in the coordinate system are equal to angles measured on the surface of the Earth. As you can imagine, conformality is a useful property for land surveyors, who make their livings measuring angles. (Surveyors measure distances too, but unfortunately there is no map projection that can preserve true distances everywhere within a plane coordinate system.) Let's consider these two types of map projections briefly.
Like most map projections, the Transverse Mercator projection is actually a mathematical transformation. The illustration below in Figure 2.26.2 may help you understand how the math works. Conceptually, the Transverse Mercator projection transfers positions on the globe to corresponding positions on a cylindrical surface, which is subsequently cut from end to end and flattened. In the illustration, the cylinder is tangent to (touches) the globe along one line, the standard line (specifically, the standard meridian). As shown in the little world map beside the globe and cylinder, scale distortion is minimal along the standard line and increases with distance from it.
The distortion ellipses plotted in red help us visualize the pattern of scale distortion associated with a generic Transverse Mercator projection. Had no distortion occurred in the process of projecting the map shown below, all of the ellipses would be the same size, and circular in shape. As you can see, the ellipses plotted along the central meridian are all the same size and circular shape. Away from the central meridian, the ellipses steadily increase in size, although their shapes remain uniformly circular. This pattern reflects the fact that scale distortion increases with distance from the standard line. Furthermore, the ellipses reveal that the character of distortion associated with this projection is that shapes of features as they appear on a globe are preserved while their relative sizes are distorted. By preserving true angles, conformal projections like the Mercator (including its transverse and oblique variants) also preserve shapes.

SPC zones that trend west to east (including Pennsylvania's) are based on unique Lambert Conformal Conic projections. Instead of the cylindrical projection surface used by projections like the Mercator, the Lambert Conformal Conic and map projections like it employ conical projection surfaces like the one shown below in Figure 2.26.3. Notice the two lines at which the globe and the cone intersect. Both of these are standard lines; specifically, standard parallels. The latitudes of the standard parallels selected for each SPC zones minimize scale distortion throughout that zone.
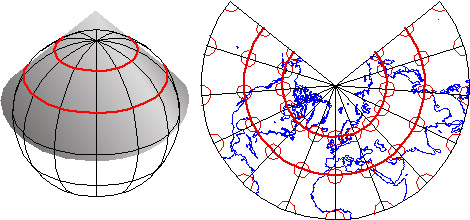
26. SPC Zone Characteristics
In consultation with various state agencies, the National Geodetic Survey (NGS) originally devised the State Plane Coordinate System in the 1930s with several design objectives in mind. Chief among these were:
- plane coordinates for ease of use in calculations of distances and areas;
- all positive values to minimize calculation errors; and
- a maximum error rate of 1 part in 10,000.
Plane coordinates specify positions in flat grids. Map projections are needed to transform latitude and longitude coordinates to plane coordinates. The designers did two things to minimize the inevitable distortion associated with map projections. First, they divided each state into zones small enough to meet the 1 part in 10,000 error threshold. Second, they used slightly different map projection formulae for each zone. The curved, dashed red lines in the illustration below for Figure 2.27.1 represent the two standard parallels that pass through each zone. The latitudes of the standard lines are one of the parameters of the Lambert Conic Conformal projection that can be customized to minimize distortion within the zone.
Positions in any coordinate system are specified relative to an origin. SPC zone origins are defined so as to ensure that every easting and northing in every zone are positive numbers. As shown in the illustration below, SPC origins are positioned south of the counties included in each zone. The origins coincide with the central meridian of the map projection upon which each zone is based. The easting and northing values at the origins are not 0, 0. Instead, eastings are defined as positive values sufficiently large to ensure that every easting in the zone is also a positive number. The false origin of the Pennsylvania North zone, for instance, is defined as 600,000 meters East, 0 meters North. Origin eastings vary from zone to zone from 200,000 to 8,000,000 meters East.

The State Plane Coordinate System will be affected by NGS' National Spatial Reference System modernization that was planned for 2022. in the new system, each state will have several "layered" plane coordinate systems, including a statewide layer for ease of use in GIS analyses, and one or "default" layers made up of zones that minimize distortion for surveying and engineering applications. You can read up on SPCS 2022 at the National Geodetic Survey's web site.

27. Map Projections
Latitude and longitude coordinates specify point locations within a coordinate system grid that is fitted to sphere or ellipsoid that approximates the Earth's shape and size. To display extensive geographic areas on a page or computer screen, as well as to calculate distances, areas, and other quantities most efficiently, it is necessary to flatten the Earth.

Georeferenced plane coordinate systems like the Universal Transverse Mercator and State Plane Coordinates systems (examined elsewhere in this chapter) are created by first flattening the graticule, then superimposing a rectangular grid over the flattened graticule. The first step, transforming the geographic coordinate system grid from a more-or-less spherical shape to a flat surface, involves systems of equations called map projections.
Many different map projection methods exist. Although only a few are widely used in large-scale mapping, the projection parameters used vary greatly. Geographic information systems professionals are expected to be knowledgeable enough to select a map projection that is suitable for a particular mapping objective. Such professionals are expected to be able to recognize the type, amount, and distribution of geometric distortion associated with different map projections. Perhaps most important, they need to know about the parameters of map projections that must be matched in order to merge geographic data from different sources. The pages that follow introduce the key concepts. The topic is far too involved to master in one section of a single chapter, however. Indeed, Penn State offers an entire online course in Map Projections: Spatial Reference Systems in GIS (GEOG 861). If you are or plan to become, a GIS professional, you should own at least one good book on map projections. Several recommendations follow in the bibliography at the end of this chapter.
Students who successfully complete this section should be able to:
- interpret distortion diagrams to identify geometric properties of the sphere that are preserved by a particular projection;
- classify projected graticules by projection family.
28. Geometric Properties Preserved and Distorted
Many types of map projections have been devised to suit particular purposes. No projection allows us to flatten the globe without distorting it, however. Distortion ellipses help us to visualize what type of distortion a map projection has caused, how much distortion has occurred, and where it has occurred. The ellipses show how imaginary circles on the globe are deformed as a result of a particular projection. If no distortion had occurred in the process of projecting the map shown below in Figure 2.29.1, all of the ellipses would be the same size, and circular in shape.
When positions on the graticule are transformed to positions on a projected grid, four types of distortion can occur: distortion of sizes, angles, distances, and directions. Map projections that avoid one or more of these types of distortion are said to preserve certain properties of the globe.
Equivalence

So-called equal-area projections maintain correct proportions in the sizes of areas on the globe and corresponding areas on the projected grid (allowing for differences in scale, of course). Notice that the shapes of the ellipses in the Cylindrical Equal Area projection above (Figure 2.29.1) are distorted, but the areas each one occupies are equivalent. Equal-area projections are preferred for small-scale thematic mapping, especially when map viewers are expected to compare sizes of area features like countries and continents.
Conformality

The distortion ellipses plotted on the conformal projection shown above in Figure 2.29.2 vary substantially in size, but are all the same circular shape. The consistent shapes indicate that conformal projections (like this Mercator projection of the world) preserve the fidelity of angle measurements from the globe to the plane. In other words, an angle measured by a land surveyor anywhere on the Earth's surface can be plotted on at its corresponding location on a conformal projection without distortion. This useful property accounts for the fact that conformal projections are almost always used as the basis for large scale surveying and mapping. Among the most widely used conformal projections are the Transverse Mercator, Lambert Conformal Conic, and Polar Stereographic.
Conformality and equivalence are mutually exclusive properties. Whereas equal-area projections distort shapes while preserving fidelity of sizes, conformal projections distort sizes in the process of preserving shapes.
Equidistance

Equidistant map projections allow distances to be measured accurately along straight lines radiating from one or two points only. Notice that ellipses plotted on the Cylindrical Equidistant (Plate Carrée) projection shown above (Figure 2.29.3) vary in both shape and size. The north-south axis of every ellipse is the same length, however. This shows that distances are true-to-scale along every meridian; in other words, the property of equidistance is preserved from the two poles. See chapters 11 and 12 of the online publication Matching the Map Projection to the Need to see how projections can be customized to facilitate distance measurements and to effectively depict ranges and rings of activity.
Azimuthality

Azimuthal projections preserve directions (azimuths) from one or two points to all other points on the map. See how the ellipses plotted on the gnomonic projection, shown above in Figure 2.29.4, vary in size and shape, but are all oriented toward the center of the projection? In this example, that's the one point at which directions measured on the globe are not distorted on the projected graticule.
Compromise

Some map projections preserve none of the properties described above, but instead seek a compromise that minimizes distortion of all kinds. The example shown above in Figure 2.29.5 is the Polyconic projection, which was used by the U.S. Geological Survey for many years as the basis of its topographic quadrangle map series until it was superceded by the conformal Transverse Mercator. Another example is the Robinson projection, which is often used for small-scale thematic maps of the world.

29. Classifying Projection Methods
The term "projection" implies that the ball-shaped net of parallels and meridians is transformed by casting its shadow upon some flat, or flattenable, surface. In fact, almost all map projection methods are mathematical equations. The analogy of an optical projection onto a flattenable surface is useful, however, as a means to classify the bewildering variety of projection equations devised over the past two thousand years or more.

Imagine a model globe that is translucent, and contains a bright light bulb. Imagine the light literally casting shadows of the graticule, and of the shapes of the continents, onto another surface that touches the globe. As you might imagine, the appearance of the projected grid will change quite a lot depending on the type of surface it is projected onto, and how that surface is aligned with the globe. The three surfaces shown above in Figure 2.30.1--the disk-shaped plane, the cone, and the cylinder--represent categories that account for the majority of projection equations that are encoded in GIS software. All three are shown in their normal aspects. The plane often is centered upon a pole. The cone is typically aligned with the globe such that its line of contact (tangency) coincides with a parallel in the mid-latitudes. And the cylinder is frequently positioned tangent to the equator (unless it is rotated 90°, as it is in the Transverse Mercator projection). The following illustrations in Figure 2.30.2 show some of the projected graticules produced by projection equations in each category.

Cylindric projection equations yield projected graticules with straight meridians and parallels that intersect at right angles. The example shown above at top left in Figure 2.30.2 is a Cylindrical Equidistant (also called Plate Carrée or geographic) in its normal equatorial aspect.
Pseudocylindric projections are variants on cylindrics in which meridians are curved. The result of a Sinusoidal projection is shown above at top right of Figure 2.30.2.
Conic projections yield straight meridians that converge toward a single point at the poles, parallels that form concentric arcs. The example shown above, at bottom left in Figure 2.30.2, is the result of an Albers Conic Equal Area, which is frequently used for thematic mapping of mid latitude regions.
Planar projections also yield meridians that are straight and convergent, but parallels form concentric circles rather than arcs. Planar projections are also called azimuthal because every planar projection preserves the property of azimuthality. The projected graticule shown above at bottom right of Figure 2.30.2 is the result of an Azimuthal Equidistant projection in its normal polar aspect.
Appearances can be deceiving. It's important to remember that the look of a projected graticule depends on several projection parameters, including latitude of projection origin, central meridian, standard line(s), and others. Customized map projections may look entirely different from the archetypes described above.
Try This!
The Interactive Album of Map Projections 2.0 is an application developed by the Penn State Online Geospatial Education Programs and is an update of an earlier site that was inspired by the USGS Professional Paper 1453, An Album of Map Projections, by John P. Snyder and Philip M. Voxland.
Flex Projector is a free, open source software program developed in Java that supports many more projections and variable parameters than the Interactive Album. Bernhard Jenny of the Institute of Cartography at ETH Zurich created the program with assistance from Tom Patterson of the US National Park Service. You can download Flex Projector from flexprojector.com
Those who wish to explore map projections in greater depth than is possible in this text might wish to visit an informative page published by the International Institute for Geo-Information Science and Earth Observation (Netherlands), which is known by the legacy acronym ITC.

30. Summary
In this chapter, we've explored several connotations of the term scale. Scale is synonymous with scope when it is used to describe the extent of a phenomenon. In this sense, "large scale" means "large area." Specialists in geographic information often use the term differently, however. Map scale refers to the relative sizes of features on a map and of corresponding objects on the ground. In this context, "large scale" implies "small area." Large scale also implies greater detail and greater accuracy, an important point to keep in mind when using maps as sources for GIS databases. Map scale is defined mathematically as the proportion of map distance to ground distance. I hope you are now prepared to use scale equations to calculate map scale.
Scale can also be thought of as a reference system for measurement. Locations on the globe are specified with reference to the geographic coordinate system of latitudes and longitudes. Plane coordinates are often preferred over geographic coordinates because they ease calculations of distance, area, and other quantities. Georeferenced plane coordinate systems like UTM and SPC are established by first flattening the graticule, then superimposing a plane coordinate grid. The mathematical equations used to transform geographic coordinates into plane coordinates are called map projections. Both plane and geographic coordinate system grids are related to approximations of the Earth's size and shape called ellipsoids. Relations between grids and ellipsoids are called horizontal datums.
Horizontal datum is an elusive concept for many GIS practitioners. It is relatively easy to visualize a horizontal datum in the context of unprojected geographic coordinates. Simply drape the latitude and longitude grid over an ellipsoid and there's your horizontal datum. It is harder to think about datum in the context of a projected coordinate grid like UTM and SPC, however. Think of it this way: First drape the latitude and longitude grid on an ellipsoid. Then project that grid to a 2-D plane surface. Then, superimpose a rectangular grid of eastings and northings over the projection, using control points to georegister the grids. There you have it--a projected coordinate grid based upon a horizontal datum.
Numerous coordinate systems, datums, and map projections are in use around the world. Because we often need to combine georeferenced data from various sources, GIS professionals need to be able to georegister two or more data sets that are based upon different coordinate systems, datums, and/or projections. Transformations, including coordinate transformations, datum transformations, and map projections, are the mathematical procedures used to bring diverse data into alignment. Characteristics of the coordinate systems, datums, and projections considered in this text are outlined in the following tables.
Coordinate systems referenced in this text
(many other national and local systems are in use)
| Coordinate System | Units | Extent | Projection Basis |
|---|---|---|---|
| Geographic | Angles (expressed as degrees, minutes, seconds or decimal degrees). | Global | None |
| UTM | Distances (meters) | Near-global (8430' N, 80° 30' S) | Unique Transverse Mercator projection for each of 60 zones |
| State Plane Coordinates | Distances (meters in SPCS 83, feet in SPCS 27) | U.S. | Unique Transverse Mercator or Lambert Conformal Conic projection for each of 123 zones (plus Oblique Mercator for Alaska panhandle) |
Datums referenced in this text
(many other national and local systems are in use)
| Datum | Horizontal or vertical | Optimized for | Reference surface |
|---|---|---|---|
| NAD 27 | Horizontal | North America | Clarke 1866 ellipsoid |
| NAD 83 | Horizontal | North America | GRS 80 ellipsoid |
| WGS 84 | Horizontal | World | WGS 84 ellipsoid |
| NAVD 88 | Vertical | North America | Sea level measured at coastal tidal stations |
Map projections referenced in this text
(many other national and local systems are in use)
| Projection name | Properties preserved | Class | Distortion |
|---|---|---|---|
| Mercator | Conformal | Cylindrical | Area distortion increases with distance from standard parallel (typically equator). |
| Transverse Mercator | Conformal | Cylindrical | Area distortion increases with distance from standard meridian. |
| Lambert Conformal Conic | Conformal | Conic | Area distortion increases with distance from one or two standard parallels. |
| Plate Carrée (sometimes called "Geographic" projection) | Equidistant | Cylindrical | Area and shape distortion increases with distance from standard parallel (typically equator). |
| Albers Equal-Area Conic | Equivalent | Conic | Shape distortion increases with distance from one or two standard parallels. |
Compiled from Snyder, 1997

31. Bibliography
(Electronic versions available at http://pubs.er.usgs.gov/djvu/PP/PP_1395.pdf)
Chapter 3: Census Data and Thematic Maps
1. Overview
In Chapter 2, we compared the characteristics of geographic and plane coordinate systems that are used to measure and specify positions on the Earth's surface. Coordinate systems, remember, are formed by juxtaposing two or more spatial measurement scales. I mentioned, but did not explain, that attribute data also are specified with reference to measurement scales. In this chapter, we'll take a closer look at how attributes are measured and represented.
Maps are both the raw material and the product of GIS. All maps, but especially so-called reference maps made to support a variety of uses, can be defined as sets of symbols that represent the locations and attributes of entities measured at certain times. Many maps, however, are subsets of available geographic data that have been selected and organized in response to a particular question. Maps created specifically to highlight the distribution of a particular phenomenon or theme are called thematic maps. Thematic maps are among the most common forms of geographic information produced by GIS.
A flat sheet of paper is an imperfect, but useful, analog for geographic space. Notwithstanding the intricacies of map projections, it is a fairly straightforward matter to plot points that stand for locations on the globe. Representing the attributes of locations on maps is sometimes not so straightforward, however. Abstract graphic symbols must be devised that depict, with minimal ambiguity, the quantities and qualities that give locations their meaning. Over the past 100 years or so, cartographers have adopted and tested conventions concerning symbol color, size, and shape for thematic maps. The effective use of graphic symbols is an important component in the transformation of geographic data into useful information.

Consider the map above (Figure 3.1.1), which shows how the distribution of U.S. population changed, by county, from 1990 to 2000. To gain a sense of how effective this thematic map is in transforming data into information, we need only to compare it to a list of population change rates for the more than 3,000 counties of the U.S. The thematic map reveals spatial patterns that the data themselves conceal.
This chapter explores the characteristics of attribute data used for thematic mapping, especially attribute data produced by U.S. Census Bureau. It also considers how the characteristics of attribute data influence choices about how to present the data on thematic maps.
Objectives
Students who successfully complete Chapter 3 should be able to:
- use metadata and the World Wide Web to assess the content and availability of attribute data produced by the U.S. Census Bureau;
- discriminate between different levels of measurement of attribute data;
- explain the differences between counts, rates, and densities, and identify the types of map symbols that are most appropriate for representing each; and
- use quantile and equal interval classification schemes to divide census attribute data into categories suitable for choroplethic mapping.
"Try This!" Activities
Take a minute to complete any of the Try This activities that you encounter throughout the chapter. These are fun, thought provoking exercises to help you better understand the ideas presented in the chapter.

2. Census Attribute Data
A thematic map is a graphic display that shows the geographic distribution of a particular attribute, or relationships among a few selected attributes. Some of the richest sources of attribute data are national censuses. In the United States, a periodic count of the entire population is required by the U.S. Constitution. Article 1, Section 2, ratified in 1787, states that Representatives and direct taxes shall be apportioned among the several states which may be included within this union, according to their respective numbers ... The actual Enumeration shall be made [every] ten years, in such manner as [the Congress] shall by law direct." The U.S. Census Bureau is the government agency charged with carrying out the decennial census.

The results of the U.S. decennial census determine states' portions of the 435 total seats in the U.S. House of Representatives. The map below shows states that lost and gained seats as a result of the reapportionment that followed the 2000 census. Congressional voting district boundaries must be redrawn within the states that gained and lost seats, a process called redistricting. Constitutional rules and legal precedents require that voting districts contain equal populations (within about 1 percent). In addition, districts must be drawn so as to provide equal opportunities for representation of racial and ethnic groups that have been discriminated against in the past.

Besides reapportionment and redistricting, U.S. census counts also affect the flow of billions of dollars of federal expenditures, including contracts and federal aid, to states and municipalities. In 1995, for example, some $70 billion of Medicaid funds were distributed according to a formula that compared state and national per capita income. $18 billion worth of highway planning and construction funds were allotted to states according to their shares of urban and rural population. And $6 billion of Aid to Families with Dependent Children was distributed to help children of poor families do better in school. The two thematic maps below (Figure 3.3.3) illustrate the strong relationship between population counts and the distribution of federal tax dollars.

The Census Bureau's mandate is to provide the population data needed to support governmental operations including reapportionment, redistricting, and allocation of federal expenditures. Its mission, to be "the preeminent collector and provider of timely, relevant, and quality data about the people and economy of the United States," is broader, however. To fulfill this mission, the Census Bureau needs to count more than just numbers of people, and it does.
Try This!

3. Enumerations versus Samples
Sixteen U.S. Marshals and 650 assistants conducted the first U.S. census in 1791. They counted some 3.9 million individuals, although as then-Secretary of State, Thomas Jefferson, reported to President George Washington, the official number understated the actual population by at least 2.5 percent (Roberts, 1994). By 1960, when the U.S. population had reached 179 million, it was no longer practical to have a census taker visit every household. The Census Bureau then began to distribute questionnaires by mail. Of the 116 million households to which questionnaires were sent in 2000, 72 percent responded by mail. A mostly-temporary staff of over 800,000 was needed to visit the remaining households, and to produce the final count of 281,421,906. Using statistically reliable estimates produced from exhaustive follow-up surveys, the Bureau's permanent staff determined that the final count was accurate to within 1.6 percent of the actual number (although the count was less accurate for young and minority residences than it was for older and white residents). It was the largest and most accurate census to that time. (Interestingly, Congress insists that the original enumeration or "head count" be used as the official population count, even though the estimate calculated from samples by Census Bureau statisticians is demonstrably more accurate.)
The mail-in response rate for the 2010 census was also 72 percent. As with most of the 20th century censuses the official 2010 census count, by state, had to be delivered to the Office of the President by December 31 of the census year. Then within one week of the opening of the next session of the Congress, the President reported to the House of Representatives the apportionment population counts and the number of Representatives to which each state was entitled.
In 1791, census takers asked relatively few questions. They wanted to know the numbers of free persons, slaves, and free males over age 16, as well as the sex and race of each individual. (You can view photos of historical census questionnaires here) As the U.S. population has grown, and as its economy and government have expanded, the amount and variety of data collected has expanded accordingly. In the 2000 census, all 116 million U.S. households were asked six population questions (names, telephone numbers, sex, age and date of birth, Hispanic origin, and race), and one housing question (whether the residence is owned or rented). In addition, a statistical sample of one in six households received a "long form" that asked 46 more questions, including detailed housing characteristics, expenses, citizenship, military service, health problems, employment status, place of work, commuting, and income. From the sampled data, the Census Bureau produced estimated data on all these variables for the entire population.
In the parlance of the Census Bureau, data associated with questions asked of all households are called 100% data and data estimated from samples are called sample data. Both types of data are available aggregated by various enumeration areas, including census block, block group, tract, place, county, and state (see the illustration below). Through 2000, the Census Bureau distributes the 100% data in a package called the "Summary File 1" (SF1) and the sample data as "Summary File 3" (SF3). In 2005, the Bureau launched a new project called American Community Survey that surveys a representative sample of households on an ongoing basis. Every month, one household out of every 480 in each county or equivalent area receives a survey similar to the old "long form." Annual or semi-annual estimates produced from American Community Survey samples replaced the SF3 data product in 2010.
To protect respondents' confidentiality, as well as to make the data most useful to legislators, the Census Bureau aggregates the data it collects from household surveys to several different types of geographic areas. SF1 data, for instance, are reported at the block or tract level. There were about 8.5 million census blocks in 2000. By definition, census blocks are bounded on all sides by streets, streams, or political boundaries. Census tracts are larger areas that have between 2,500 and 8,000 residents. When first delineated, tracts were relatively homogeneous with respect to population characteristics, economic status, and living conditions. A typical census tract consists of about five or six sub-areas called block groups. As the name implies, block groups are composed of several census blocks. American Community Survey estimates, like the SF3 data that preceded them, are reported at the block group level or higher.

- Nation
- Zip Codes
- Zip Code Tabulation Areas
- Urban Areas
- Metropolitan Areas
- American Indian, Alaska Native & Native Hawaiian Areas
- Regions
- Divisions
- States
- School Districts
- Congressional Districts
- Economic Places
- Oregon Urban Growth Areas
- State Legislative Districts
- Alaska Native Regional Corporations
- Places
- Counties
- Voting Districts
- Traffic Analysis Zones
- County Subdivisions
- Subbarrios
- Census Tracts
- Block Groups
- Blocks
- Zip Codes
- Zip Code Tabulation Areas
- Urban Areas
- Metropolitan Areas
- American Indian, Alaska Native & Native Hawaiian Areas
- School Districts
- Congressional Districts
- Economic Places
- Oregon Urban Growth Areas
- State Legislative Districts
- Alaska Native Regional Corporations
- Places
- Voting Districts
- Traffic Analysis Zones
- County Subdivisions
- Subbarrios

4. American Community Survey
Beginning in 2010, the American Community Survey (ACS) replaced the "long form" that was used to collect sample data in past decennial censuses. Instead of sampling one in six households every ten years (about 18 million households in 2000), the ACS samples 2-3 million households every year. The goal of the ACS is to enable Census Bureau statisticians to produce more timely estimates of the demographic, economic, social, housing, and financial characteristics of the U.S. population. You can view a sample ACS questionnaire by entering the keywords "American Community Survey questionnaire" into your favorite Internet search engine.
Try This!
Acquiring and Understanding American Community Survey (ACS) Data
The purpose of this practice activity is to guide your exploration of ACS data and methodology. In the end, you should be able to identify the types of geographical areas for which ACS data are available; to explain why 1-year and 3-year estimates are available for some areas and not for others; and to describe how the statistical reliability of ACS estimates vary among 1-year, 3-year, and 5-year estimates.
- Return to the U.S. Census Bureau site.
- Click the Surveys/Programs tab and follow the link to American Community Survey (ACS). This takes you to the MAIN American Community Survey page.
- Begin by clicking the Guidance for Data Users link and looking through the information available there.
Note the link to Handbooks for Data Users.
Under the More Guidance for Data Users Topics heading, pay particular attention to the When to use… section with its descriptions of the various estimates (1-, 3- and 5-year), and to the section on Comparing ACS Data to other census data. If you are so inclined, there is also a link to a listing of Training Presentations under this same heading. (You might benefit from Understanding Multiyear Estimates... offering.) - Next, hover your mouse cursor over the Data link located in the navigation list on the left side of the ACS page, and note what entries are there:
You can download ACS data to make maps and analyses using your own GIS or statistical software. Find download links and pertinent information in the sections titled Data via FTP and Summary File Data.
There is also a section pertaining to Public Use Microdata Sample (PUMS). PUMS data are edited, however, to protect the confidentiality of individuals and households.
In the remaining steps, you will make a map or two to reinforce the geographies covered by the American Community Survey. You will map data from your home (or adopted) state. - You first need to go to the MAIN American FactFinder site, then follow the Advanced Search / SHOW ME ALL link, click the Topics search box, then expand the Program list and choose American Community Survey. Close the Select Topics overlay window.)
- Click the Geographies search options box (on the left) to reveal the Select Geographies overlay window.
Under Select, a geographic type, click County - 050.
Next, from the Select a state list, choose your state.
Then, from the Select one or more geographic areas... list, choose All Counties within <your state>.
Then, click ADD TO YOUR SELECTIONS. This will add the All Counties… entry to the Your Selections list.
Close the Select Geographies overlay window. - In the Search Results window, note that there are many datasets that have 1-, 3- and 5-year estimates entries.
Decide upon a 1-Year dataset to look at and check the box for it.
Then click View.
On the new Table Viewer page that you land on, be sure that the Create a Map choice is blue – not grayed out. (If it is grayed out, click the BACK TO ADVANCED SEARCH button and make sure only one dataset box is checked, or make a different choice, then click View again.)
Click on Create a Map. The data values in the table will turn blue, and you will be prompted to “Click on a data value in the table to map.” Clicking a single data value from any row will allow you to map the data in that row for all of the counties for which it is available. Click on a blue data value of your choice – remember which row you choose. Click on the SHOW MAP button in the small popup window that appears.Are all of the counties in the state symbolized as having data? Why not?
- Now, click the BACK TO ADVANCED SEARCH button. Un-check the box for the 1-year dataset, and check the box for the 5-year estimate of the same category. Proceed as above to map the data. After the map is refreshed, note how many counties now exhibit data.
Take a look at the 3-year estimates for the same dataset if you wish, though they may not be available for the more recent years.

5. International Data
The International Data Base is published on the web by the Census Bureau's International Programs Center. It combines demographic data compiled from censuses and surveys of some 227 countries and areas of the world, along with estimates produced by Census Bureau demographers. Data variables include population by age and sex; vital rates, infant mortality, and life tables; fertility and child survivorship; migration; marital status; family planning; ethnicity, religion, and language; literacy; and labor force, employment, and income. Census and survey data are available by country for selected years from 1950; projected data are available through 2050. The International Data Base allows you to download attribute data in formats appropriate for thematic mapping.
Try This!
Acquiring World Demographic Data via the World Wide Web
The purpose of this practice activity is to guide you through the process of finding and acquiring demographic data for the countries of the world from the U.S. Census Bureau data via the web. Your objective is to retrieve population change rates for a country of your choice over two or more years.
- Return to the U.S. Census Bureau site.
- Click the Topics tab, expand the Population list and click on International. That will take you to the International Programs page.
Click on the Data tab and then click on International Data Base (IDB). - Choose a data theme you are interested in from the Select Report pick list. The choices have to do with births and mortality, population change including such things as migration, population by age group, etc. (The Population Pyramid Graph choice gives you
a graph(s) rather than a data table.)
Data tables are available by Country or by Region.
From the Select one or more Countries or Areas pick list, you can specify that you want data for a single country or for a collection of countries, and from the Select up to 25 Years pick list you can specify that you want data for more than a single year. See the instructions in small text at the bottom of the window on how to select multiple entries from the selection boxes.
From the Select Region(s) selection box, you can choose from pre-selected groupings of countries. - Now, choose a single country under Country Search and select two or more years from the Select up to 25 Years pick list.
Then click SUBMIT.
You will see a summary table or plot of the data for your selected country and years. - Click the Search button to go back and experiment with the choices in the Select Region(s) selection box and the Aggregation Options choice list.
For your information: to download an Excel (.xls) or an comma-delimited text file (.csv) version of the data, find the respective link on the Results page: "Excel" or "CSV"
Download links may not appear when the search has been broad.

6. Counts, Rates, and Densities
The raw data collected during decennial censuses are counts--whole numbers that represent people and housing units. The Census Bureau aggregates counts to geographic areas such as counties, tracts, block groups, and blocks, and reports the aggregate totals. In other cases, summary measures, such as averages and medians, are reported. Counts can be used to ensure that redistricting plans comply with the constitutional requirement that each district contain equal population. Districts are drawn larger in sparsely populated areas, and smaller where population is concentrated. Counts, averages, and medians cannot be used to determine that districts are drawn so that minority groups have an equal probability of representation, however. For this, pairs of counts must be converted into rates or densities. A rate, such as Hispanic population as a percentage of total population, is produced by dividing one count by another. A density, such as persons per square kilometer, is a count divided by the area of the geographic unit to which the count was aggregated. In this chapter, we'll consider how the differences between counts, rates, and densities influence the ways in which the data may be processed in geographic information systems and displayed on thematic maps.
7. Attribute Measurement Scales
Chapter 2 focused upon measurement scales for spatial data, including map scale (expressed as a representative fraction), coordinate grids, and map projections (methods for transforming three dimensional to two dimensional measurement scales). You may know that the meter, the length standard established for the international metric system, was originally defined as one-ten-millionth of the distance from the equator to the North Pole. In virtually every country except the United States, the metric system has benefited science and commerce by replacing fractions with decimals, and by introducing an Earth-based standard of measurement.
Standardized scales are needed to measure non-spatial attributes as well as spatial features. Unlike positions and distances, however, attributes of locations on the Earth's surface are often not amenable to absolute measurement. In a 1946 article in Science, a psychologist named S. S. Stevens outlined a system of four levels of measurement meant to enable social scientists to systematically measure and analyze phenomena that cannot simply be counted. (In 1997, geographer Nicholas Chrisman pointed out that a total of nine levels of measurement are needed to account for the variety of geographic data.) The levels are important to specialists in geographic information because they provide guidance about the proper use of different statistical, analytical, and cartographic operations. In the following, we consider examples of Stevens' original four levels of measurement: nominal, ordinal, interval, and ratio.
8. Nominal Level
Data produced by assigning observations into unranked categories are said to be nominal level measurements. Nominal categories can be differentiated and grouped into categories, but cannot logically be ranked from high to low (unless they are associated with preferences or other exogenous value systems). For example, one can classify the land cover at a certain location as woods, scrub, orchard, vineyard, or mangrove. One cannot say, however, that a location classified as "woods" is twice as vegetated as another location classified "scrub." The phenomenon "vegetation" is a set of categories, not range of numerical values, and the categories are not ranked. That is, "woods" is in no way greater than "mangrove," unless the measurement is supplemented by a preference or priority.

Although census data originate as counts, much of what is counted is individuals' membership in nominal categories. Race, ethnicity, marital status, mode of transportation to work (car, bus, subway, railroad...), type of heating fuel (gas, fuel oil, coal, electricity...), all are measured as numbers of observations assigned to unranked categories. For example, the map below in Figure 3.9.2, which appears in the Census Bureau's first atlas of the 2000 census, highlights the minority groups with the largest percentage of population in each U.S. state. Colors were chosen to differentiate the groups, but not to imply any quantitative ordering.

9. Ordinal Level
Like the nominal level of measurement, ordinal scaling assigns observations to discrete categories. Ordinal categories are ranked, however. It was stated in the preceding page that nominal categories such as "woods" and "mangrove" do not take precedence over one another unless an extrinsic set of priorities is imposed upon them. In fact, the act of prioritizing nominal categories transforms nominal level measurements to the ordinal level.

Examples of ordinal data often seen on reference maps include political boundaries that are classified hierarchically (national, state, county, etc.) and transportation routes (primary highway, secondary highway, light-duty road, unimproved road). Ordinal data measured by the Census Bureau include how well individuals speak English (very well, well, not well, not at all), and level of educational attainment. Social surveys of preferences and perceptions are also usually scaled ordinally.
Individual observations measured at the ordinal level typically should not be added, subtracted, multiplied, or divided. For example, suppose two 640-acre grid cells within your county are being evaluated as potential sites for a hazardous waste dump. Say the two areas are evaluated on three suitability criteria, each ranked on a 0 to 3 ordinal scale, such that 0 = unsuitable, 1 = marginally unsuitable, 2 = marginally suitable, and 3 = suitable. Now say Area A is ranked 0, 3, and 3 on the three criteria, while Area B is ranked 2, 2, and 2. If the Siting Commission was to simply add the three criteria, the two areas would seem equally suitable (0 + 3 + 3 = 6 = 2 + 2 + 2), even though a ranking of 0 on one criterion ought to disqualify Area A.
10. Interval and Ratio Levels
Interval and ratio are the two highest levels of measurement in Stevens' original system. Unlike nominal- and ordinal-level data, which are qualitative in nature, interval- and ratio-level data are quantitative. Examples of interval level data include temperature and year. Examples of ratio level data include distance and area (e.g., acreage). The scales are similar in so far as units of measurement are arbitrary (Celsius versus Fahrenheit, Gregorian versus Islamic calendar, English versus metric units). The scales differ in that the zero point is arbitrary on interval scales, but not on ratio scales. For instance, zero degrees Fahrenheit and zero degrees Celsius are different temperatures, and neither indicates the absence of temperature. Zero meters and zero feet mean exactly the same thing, however. An implication of this difference is that a quantity of 20 measured at the ratio scale is twice the value of 10, a relation that does not hold true for quantities measured at the interval level (20 degrees is not twice as warm as 10 degrees).
Because interval and ratio level data represent positions along continuous number lines, rather than members of discrete categories, they are also amenable to analysis using inferential statistical techniques. Correlation and regression, for example, are commonly used to evaluate relationships between two or more data variables. Such techniques enable analysts to infer not only the form of a relationship between two quantitative data sets, but also the strength of the relationship.

11. Levels and Operations
One reason that it's important to recognize levels of measurement is that different measurement scales are amenable to different analytical operations (Chrisman 2002). Some of the most common operations include:
- Group: Categories of nominal and ordinal data can be grouped into fewer categories. For instance, grouping can be used to reduce the number of land use/land cover classes from, say, four (residential, commercial, industrial, parks) to one (urban).
- Isolate: One or more categories of nominal, ordinal, interval, or ratio data can be selected, and others set aside. As a hypothetical example, consider a range of georeferenced soil moisture readings taken over a farm field. A subrange of readings that are amenable to a particular fertilizer or pesticide might be isolated so that application is limited to the appropriate areas of the field.
- Cross tab: Two or more sets of nominal or ordinal categories can be associated one to another in pairs, triplets, etc. Chrisman (2002) points to the multicharacter codes used in the National Wetland Inventory as an example of a cross tab. Each position in the NWI code represents a particular attribute. Each unique code, therefore, represents a cross tabulation of the possible combinations of attributes.
- Difference: The difference of two interval level observations (such as two calendar years) results in one ratio level observation (such as one age).
- Other arithmetic operations: Two or more compatible sets of ratio or interval level data can be added, subtracted, multiplied, or divided. For example, the per capita (average) income of a census tract can be calculated by dividing the sum of the income of every individual in a census tract (a ratio level variable) by the sum of persons residing in the tract (a second ratio level variable).
- Classification: Interval and ratio data are frequently sorted into ordinal level categories for thematic mapping.

12. Thematic Mapping
Unlike reference maps, thematic maps are usually made with a single purpose in mind. Typically, that purpose has to do with revealing the spatial distribution of one or two attribute data sets.
In this section, we will consider distinctions among three types of ratio level data, counts, rates, and densities. We will also explore several different types of thematic maps, and consider which type of map is conventionally used to represent the different types of data. We will focus on what is perhaps the most prevalent type of thematic map, the choropleth map. Choropleth maps tend to display ratio level data which have been transformed into ordinal level classes. Finally, you will learn two common data classification procedures, quantiles and equal intervals.
13. Graphic Variables
Maps use graphic symbols to represent the locations and attributes of phenomena distributed across the Earth's surface. Variations in symbol size, color lightness, color hue, and shape can be used to represent quantitative and qualitative variations in attribute data. By convention, each of these "graphic variables" is used to represent a particular type of attribute data.
14. Counts, Rates, and Densities
Ratio level data predominate on thematic maps. Ratio data are of several different kinds, including counts, rates, and densities. As stated earlier, counts (such as total population) are whole numbers representing discrete entities, such as people. Rates and densities are produced from pairs of counts. A rate, such as percent population change, is produced by dividing one count (for example, population in year 2) by another (population in year 1). A density, such as persons per square kilometer, is a count divided by the area of the geographic unit to which the count was aggregated (e.g., total population divided by number of square kilometers). It is conventional to use different types of thematic maps to depict each type of ratio-level data.
15. Mapping Counts
The simplest thematic mapping technique for count data is to show one symbol for every individual counted. If the location of every individual is known, this method often works fine. If not, the solution is not as simple as it seems. Unfortunately, individual locations are often unknown, or they may be confidential. Software like ESRI's ArcMap, for example, is happy to overlook this shortcoming. Its "Dot Density" option causes point symbols to be positioned randomly within the geographic areas in which the counts were conducted. The size of dots and the number of individuals represented by each dot are also optional. Random dot placement may be acceptable if the scale of the map is small so that the areas in which the dots are placed are small. Often, however, this is not the case.

An alternative for mapping counts that lack individual locations is to use a single symbol, a circle, square, or some other shape, to represent the total count for each area. ArcMap calls the result of this approach a Proportional Symbol map. In the map shown below in Figure 3.16.2, the size of each symbol varies in direct proportion to the data value it represents. In other words, the area of a symbol used to represent the value "1,000,000" is exactly twice as great as a symbol that represents "500,000." To compensate for the fact that map readers typically underestimate symbol size, some cartographers recommend that symbol sizes be adjusted. ArcMap calls this option "Flannery Compensation" after James Flannery, a research cartographer who conducted psychophysical studies of map symbol perception in the 1950s, 60s, and 70s. A variant on the Proportional Symbol approach is the Graduated Symbol map type, in which different symbol sizes represent categories of data values rather than unique values. In both of these map types, symbols are usually placed at the mean locations, or centroids, of the areas they represent.

16. Mapping Rates and Densities
A rate is a proportion between two counts, such as Hispanic population as a percentage of total population. One way to display the proportional relationship between two counts is with what ArcMap calls its Pie Chart option. Like the Proportional Symbol map, the Pie Chart map plots a single symbol at the centroid of each geographic area by default, though users can opt to place pie symbols such that they won't overlap each other (This option can result in symbols being placed far away from the centroid of a geographic area.) Each pie symbol varies in size in proportion to the data value it represents. In addition, however, the Pie Chart symbol is divided into pieces that represent proportions of a whole.
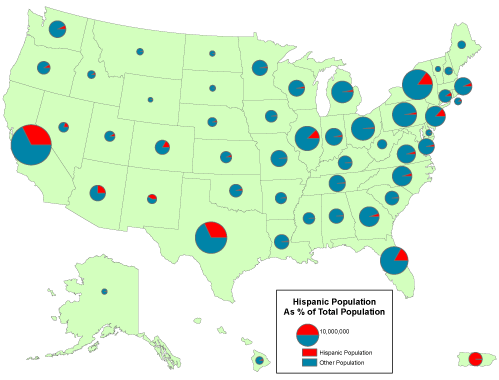
Some perceptual experiments have suggested that human beings are more adept at judging the relative lengths of bars than they are at estimating the relative sizes of pie pieces (although it helps to have the bars aligned along a common horizontal base line). You can judge for yourself by comparing the effect of ArcMap's Bar/Column Chart option.
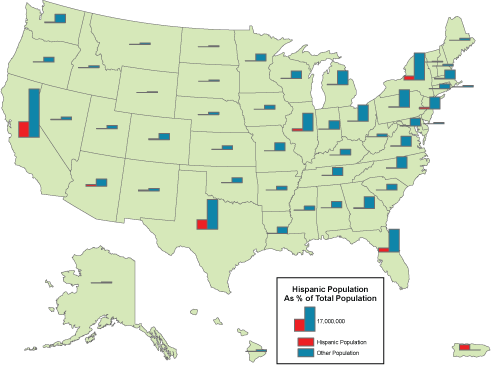
Like rates, densities are produced by dividing one count by another, but the divisor of a density is the magnitude of a geographic area. Both rates and densities hold true for entire areas, but not for any particular point location. For this reason, it is conventional not to use point symbols to symbolize rate and density data on thematic maps. Instead, cartography textbooks recommend a technique that ArcMap calls "Graduated Colors." Maps produced by this method, properly called choropleth maps, fill geographic areas with colors that represent attribute data values.
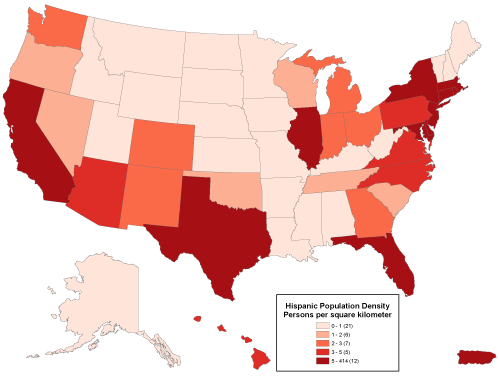
Because our ability to discriminate among colors is limited, attribute data values at the ratio or interval level are usually sorted into four to eight ordinal level categories. ArcMap calls these categories classes. Users can adjust the number of classes, the class break values that separate the classes, and the colors used to symbolize the classes. Users may choose a group of predefined colors, known as a color ramp, or they may specify their own custom colors. Color ramps are sequences of colors that vary from light to dark, where the darkest color is used to represent the highest value range. Most textbook cartographers would approve of this, since they have long argued that it is the lightness and darkness of colors, not different color hues, that most logically represent quantitative data.
Logically or not, people prefer colorful maps. For this reason some might be tempted to choose ArcMap's Unique Values option to map rates, densities, or even counts. This option assigns a unique color to each data value. Colors vary in hue as well as lightness. This symbolization strategy is designed for use with a small number of nominal level data categories. As illustrated in the map below (Figure 3.17.4), the use of an unlimited set of color hues to symbolize unique data values leads to a confusing thematic map.

17. Data Classification
You've read several times already in this text that geographic data is always generalized. As you recall from Chapter 1, generalization is inevitable due to the limitations of human visual acuity, the limits of display resolution, and especially to the limits imposed by the costs of collecting and processing detailed data. What we have not previously considered is that generalization is not only necessary, it is sometimes beneficial.
Generalization helps make sense of complex data. Consider a simple example. The graph below (Figure 3.18.1) shows the percent population change for Pennsylvania's 67 counties over a five-year period. Categories along the x axis of the graph represent each of the 49 unique percentage values (some of the counties had exactly the same rate). Categories along the y axis are the numbers of counties associated with each rate. As you can see, it's difficult to discern a pattern in these data.

The following graph shows exactly the same data set, only grouped into 7 classes. It's much easier to discern patterns and outliers in the classified data than in the unclassified data. Notice that the mass of population change rates are distributed around 0 to 5 percent, and that there are two counties (x and y counties) whose rates are exceptionally high. This information is obscured in the unclassified data.

| Percent Population Change | Number of Counties |
|---|---|
| Less than -10 | 0 |
| [-10, -5) | 1 |
| [-5, 0) | 8 |
| [0, 5) | 44 |
| [5, 10) | 10 |
| [10, 15) | 2 |
| [15, 20) | 0 |
| [20, 25) | 1 |
| [25, 30) | 0 |
| [30, 35) | 1 |
| Greater than or equal to 35 | 0 |
Data classification is a means of generalizing thematic maps. Many different data classification schemes exist. If a classification scheme is chosen and applied skillfully, it can help reveal patterns and anomalies that otherwise might be obscured. By the same token, a poorly-chosen classification scheme may hide meaningful patterns. The appearance of a thematic map, and sometimes conclusions drawn from it, may vary substantially depending on data classification scheme used.
18. Two Classification Schemes
Many different systematic classification schemes have been developed. Some produce "optimal" classes for unique data sets, maximizing the difference between classes and minimizing differences within classes. Since optimizing schemes produce unique solutions, however, they are not the best choice when several maps need to be compared. For this, data classification schemes that treat every data set alike are preferred.

Two commonly used schemes are quantiles and equal intervals ("quartiles," "quintiles," and "percentiles" are instances of quantile classifications that group data into four, five, and 100 classes respectively). The following two graphs illustrate the differences.

The graph in Figure 3.19.2 groups the Pennsylvania county population change data into five classes, each of which contains the same number of counties (in this case, approximately 20 percent of the total in each). The quantiles scheme accomplishes this by varying the width, or range, of each class.

In the second graph, Figure 3.19.3, the width or range of each class is equivalent (8 percentage points). Consequently, the number of counties in each equal interval class varies.


As you can see, the effect of the two different classification schemes on the appearance of the two choropleth maps above is dramatic. The quantiles scheme is often preferred because it prevents the clumping of observations into a few categories shown in the equal intervals map. Conversely, the equal interval map reveals two outlier counties which are obscured in the quantiles map. A good point to take from this little experiment is that it is often useful to compare the maps produced by several different map classifications. Patterns that persist through changes in classification scheme are likely to be more conclusive evidence than patterns that shift.
19. Calculating Quantile Classes
The objective of this section is to ensure that you understand how mapping programs like ArcMap classify data for choropleth maps. First, we will step through the classification of the Pennsylvania county population change data. Then you will be asked to classify another data set yourself.
Step 1: Sort the data.
Attribute data retrieved from sources like the Census Bureau's website are likely to be sorted alphabetically by geographic area. To classify the data set, you need to resort the data from the highest attribute data value to the lowest.
Step 2: Define the number of classes.
There are no absolute rules on this. Since our ability to differentiate colors is limited, the more classes you make, the harder they may be to tell apart. In general, four to eight classes are used for choropleth mapping. Use an odd number of classes if you wish to visualize departures from a central class that contains a median (or zero) value.
Step 3: Determine class breaks by dividing the number of observations by the number of classes.
For example, 67 counties divided by 5 classes yields 13.4 counties per class. Obviously, in cases like this, the number of counties in each class has to vary a little. Make sure that counties having the same value are assigned to the same class, even if that class ends up with more members than other classes.
Step 4: Assign color symbols to differentiate the categories.
Figure 3.20.1, below, shows three iterations of a data table. The first (on the left) is sorted alphabetically by county name. The middle table is sorted by percent population change, in descending order. The third table breaks the re-sorted counties into five quintile categories. Normally, you would classify the data and symbolize the map using GIS software, of course. The illustration includes the colors that were used to symbolize the corresponding choropleth map on the preceding page. If you'd like to try sorting the data table illustrated below, follow this link to open the spreadsheet file.


20. Summary
National censuses, such as the decennial census of the U.S., are among the richest sources of attribute data. Attribute data are heterogeneous. They range in character from qualitative to quantitative; from unranked categories to values that can be positioned along a continuous number line. Social scientists have developed a variety of different measurement scales to accommodate the variety of phenomena measured in censuses and other social surveys. The level of measurement used to define a particular data set influences analysts' choices about which analytical and cartographic procedures should be used to transform the data into geographic information.
Thematic maps help transform attribute data by revealing patterns obscured in lists of numbers. Different types of thematic maps are used to represent different types of data. Count data, for instance, are conventionally portrayed with symbols that are distinct from the statistical areas they represent, because counts are independent of the sizes of those areas. Rates and densities, on the other hand, are often portrayed as choropleth maps, in which the statistical areas themselves serve as symbols whose color lightness vary with the attribute data they represent. Attribute data shown on choropleth maps are usually classified. Classification schemes that facilitate comparison of map series, such as the quantiles and equal intervals schemes demonstrated in this chapter, are most common.
The U.S. Census Bureau's mandate requires it to produce and maintain spatial data as well as attribute data. In Chapter 4, we will study the characteristics of those data, which are part of a nationwide geospatial database called "TIGER."

21. Bibliography
Chapter 4: TIGER, Topology and Geocoding
1. Overview
In Chapter 3, we studied the population data produced by the U.S. Census Bureau, and some of the ways those data can be visualized with thematic maps.
In addition to producing data about the U.S. population and economy, the Census Bureau is a leading producer of digital map data. The Census Bureau's Geography Division created its "Topologically Integrated Geographic Encoding and Referencing" (TIGER) spatial database with help from the U.S. Geological Survey. In preparation for the 2010 census, the Bureau conducted a database redesign project that combined TIGER with a Master Address File (MAF) database. MAF/TIGER enables the Bureau to associate census data, which it collects by household address, with the right census areas and voting districts. This is an example of a process called address-matching or geocoding.
The MAF/TIGER database embodies the vector approach to spatial representation. It uses point, line, and polygon features to represent streets, water bodies, railroads, administrative boundaries, and select landmarks. In addition to the "absolute" locations of these features, which are encoded with latitude and longitude coordinates, MAF/TIGER encodes their "relative" locations--a property called topology.
MAF/TIGER also includes attributes of these vector features including names, administrative codes, and, for many streets, address ranges and ZIP Codes. Vector feature sets are extracted from the MAF/TIGER database to produce reference maps for census takers and thematic maps for census data users. Such extracts are called TIGER/Line Shapefiles.
Characteristics of TIGER/Line Shapefiles that make them useful to the Census Bureau also make them valuable to other government agencies and businesses. Because they are not protected by copyright, TIGER/Line data have been widely adapted for many commercial uses. TIGER has been described as "the first truly useful nationwide general-purpose spatial data set" (Cooke 1997, p. 47). Some say that it jump-started a now-thriving geospatial data industry in the U.S.
Objectives
The objective of this chapter is to familiarize you with MAF/TIGER and two important concepts it exemplifies: topology and geocoding. Specifically, students who successfully complete Chapter 4 should be able to:
- explain how geographic entities are represented within MAF/TIGER;
- explain how geometric primitives in MAF/TIGER are represented in TIGER/Line Shapefile extracts;
- define topology and explain why and how it is encoded in TIGER;
- perform address geocoding; and
- describe how TIGER/Line files and similar products can be used for other applications, including routing and allocation.
"Try This!" Activities
Take a minute to complete any of the Try This activities that you encounter throughout the chapter. These are fun, thought provoking exercises to help you better understand the ideas presented in the chapter.
Concept Map
You may be interested in seeing the concept map used to guide development of Chapters 3 and 4. The concept map delineates the entities and relationships that make up the contents of the two chapters.

2. MAF/TIGER
MAF/TIGER is the Census Bureau's geographic database system. Several factors prompted the U.S. Census Bureau to create MAF/TIGER: the need to conduct the census by mail, the need to produce wayfinding aids for census field workers, and its mission to produce map and data products for census data users.
Conducting the census by mail
As the population of the U.S. increased, it became impractical to have census takers visit every household in person. Since 1970, the Census Bureau has mailed questionnaires to most households, with instructions that completed forms should be returned by mail. Most, but certainly not all, of these questionnaires, are dutifully mailed—about 72 percent of all questionnaires in 2010. At that rate, the Census Bureau estimates that some $1.6 billion was saved by reducing the need for field workers to visit non-responding households.

To manage its mail delivery and return operations, the Census Bureau relies upon a Master Address File (MAF). MAF is a complete inventory of housing units and many business locations in the U.S., Puerto Rico, and associated island areas. MAF was originally built from the U.S. Postal Service’s Delivery Sequence File of all residential addresses. The MAF is updated through both corrections from field operations and a Local Update of Census Address (LUCA) program by which tribal, state, and local government liaisons review and suggest updates to local address records. “MAF/TIGER” refers to the coupling of the Master Address File with the TIGER spatial database, which together enables the Census Bureau to efficiently associate address-referenced census and survey data received by mail with geographic locations on the ground and tabulation areas of concern to Congress and many governmental agencies and businesses.
It’s not as simple as it sounds. Postal addresses do not specify geographic locations precisely enough to fulfill the Census Bureau’s constitutional mandate. An address is not a position in a grid coordinate system--it is only one in a series of ill-defined positions along a route. The location of an address is often ambiguous because street names are not unique, numbering schemes are inconsistent, and because routes have two sides, left and right. Location matters, as you recall, because census data must be accurately georeferenced to be useful for reapportionment, redistricting, and allocation of federal funds. Thus, the Census Bureau had to find a way to assign address referenced data automatically to particular census blocks, block groups, tracts, voting districts, and so on. That's what the "Geographic Encoding and Referencing" in the TIGER acronym refers to.
Maps for Census Field Workers
A second motivation that led to MAF/TIGER was the need to help census takers find their way around. Millions of households fail to return questionnaires by mail, after all. Census takers (called “enumerators” at the Bureau) visit non-responding households in person. Census enumerators need maps showing streets and select landmarks to help locate households. Census supervisors need maps to assign census takers to particular territories. Field notes collected by field workers are an important source of updates and corrections to the MAF/TIGER database.
Prior to 1990, the Bureau relied on local sources for its maps. For example, 137 maps of different scales, quality, and age were used to cover the 30-square-mile St. Louis area during the 1960 census. The need for maps of consistent scale and quality forced the Bureau to become a map maker as well as a map user. Using the MAF/TIGER system, Census Bureau geographers created over 17 million maps for a variety of purposes in preparation for the 2010 Census.
Data Products
The Census Bureau's mission is not only to collect data, but also to make data products available to its constituents. In addition to the attribute data considered in Chapter 3, the Bureau disseminates a variety of geographic data products, including wall maps, atlases, and one of the earliest online mapping services, the TIGER Mapping Service. You can explore the Bureau's maps and cartographic data products here.

MAF/TIGER Database Redesign
The Census Bureau conducted a major redesign of the MAF/TIGER database in the years leading up to the 2010 decennial census. What were separate, homegrown database systems (MAF and TIGER) are now unified in the industry-standard Oracle relational database management system. Benefits of this “commercial off-the-shelf” (COTS) database software include concurrent multi-user access, greater user familiarity, and better integration with web development tools. As Galdi (2005) explains in his white paper, “Spatial Data Storage and Topology in the Redesigned MAF/TIGER System,” the redesign “mirrors a common trend in the Information Technology (IT) and Geographic Information System (GIS) industries: the integration of spatial and non-spatial data into a single enterprise data set” (p. 2).
Concurrent with the MAF/TIGER redesign, the Census Bureau also updated the distribution format of its TIGER/Line map data extracts. Consistent with the Bureau’s COTS strategy, it adopted the de facto standard Esri “Shapefile” format. The following pages consider characteristics of the spatial data stored in MAF/TIGER and in TIGER/Line Shapefile extracts.
3. Vector Extracts from MAF/TIGER
The Census Bureau began to develop a digital geographic database of 144 metropolitan areas in the 1960s. By 1990, the early efforts had evolved into TIGER: a seamless digital geographic database that covered the whole of the United States and its territories. As discussed in the previous page, MAF/TIGER succeeded TIGER in the lead-up to the 2010 Census.
TIGER/Line Shapefiles are digital map data products extracted from the MAF/TIGER database. They are freely available from the Census Bureau and are suitable for use by individuals, businesses, and other agencies that don’t have direct access to MAF/TIGER.
This section outlines the geographic entities represented in the MAF/TIGER database, describes how a particular implementation of the vector data model is used to represent those entities, and considers the accuracy of digital features in relation to their counterparts on the ground. The following page considers characteristics of the “Shapefile” data format used to distribute digital extracts from MAF/TIGER.
Geographies Represented in TIGER and Shapefile Extracts
The MAF/TIGER database is selective. Only those geographic entities needed to fulfill the Census Bureau’s operational mission are included. Entities that don't help the Census Bureau conduct its operations by mail, or help field workers navigate a neighborhood, are omitted. Terrain elevation data, for instance, are not included in MAF/TIGER. A comprehensive list of the "feature classes” and “superclasses” included in MAF/TIGER and Shapefiles can be found via the MAF/TIGER Feature Class Codes (MTFCCs) link on the list of Geographic Codes on the Census.gov > Geography > Reference page. Examples of superclasses include:
- potential living quarters (e.g., sites of shelters, retirement homes, prisons, dormitories);
- road/path features (e.g., primary roads, secondary roads, local neighborhood roads);
- hydrographic features (e.g., stream/river, lake/pond, ocean/sea);
- miscellaneous linear features (e.g., pipeline, powerline, fence line);
- tabulation areas (e.g., county or equivalent, tract, block group, block).
| MTFCC | FEATURE CLASS | SUPERCLASS | POINT | LINEAR | AREAL | FEATURE CLASS DESCRIPTION |
|---|---|---|---|---|---|---|
| S1400 | Local Neighborhood Road, Rural Road, City Street | Road/Path Features | N | Y | N | Generally a paved non-arterial street, road, or byway that usually has a single lane of traffic in each direction. Roads in this feature class may be privately or publicly maintained. Scenic park roads would be included in this feature class, as would (depending on the region of the country) some unpaved roads. |
| S1500 | Vehicular Trail (4WD) | Road/Path Features | N | Y | N | An unpaved dirt trail where a four-wheel drive vehicle is required. These vehicular trails are found almost exclusively in very rural areas. Minor, unpaved roads usable by ordinary cars and trucks belong in the S1400 category. |
| S1630 | Ramp | Road/Path Features | N | Y | N | A road that allows controlled access from adjacent roads onto a limited access highway, often in the form of a cloverleaf interchange. These roads are unaddressable. |
Note also that neither the MAF/TIGER database nor TIGER/Line Shapefiles include the population data collected through questionnaires and by census takers. MAF/TIGER merely provides the geographic framework within which address-referenced census data are tabulated.
Try This!
Exploring Available TIGER/Line Shapefiles
In this Try This! (One of 3 dealing with TIGER/Line Shapefiles), you are going to explore which TIGER/Line Shapefiles are available for download at various geographies and what information those files contain. We will be exploring the 2009 and 2010 versions of the TIGER/Line Shapefile data sets. Versions from other years are available. Feel free to investigate those, too.
- Follow this link to get to the TIGER Products page of the Census Bureau website, then follow the TIGER/Line Shapefiles link found under Which product should I use? to get to the Geography page.
- Link to the 2010 TIGER/Line Shapefiles via the 2010 tab link.
- Select Download, and then, from the expanded list, choose Web Interface.
- Expand the pick list under Select a layer type. Spend some time choosing different entries from the layer pick list and then, using the Submit button to navigate through the sub layers, taking note of when you are offered access to a Download button. Take note of a couple of things. (1) Some of the pick lists make a selection available that allows you to download a shapefile dataset for the entire country. (2) For some of the choices, you must navigate to the County level before the Download button is available.
- Before you continue, click on the TIGER/Line Shapefiles Main link to get back to the TIGER/Line Shapefiles page.
As stated above, we want you to get a sense of the sorts of data that are available for the various geographies -- from the county to the national level. Perusing the various layers as I had you doing above makes it difficult to make an overall assessment of what data there are at a given geographic scale. Fortunately for our purposes, the Census has provided a convenient table to help us in this regard.
From the TIGER/Line Shapefiles page,
- Select the 2010 tab again.
- Select File Availability.
Study the table that appears. - Note that there are columns titled State- and County-based Files, Nation-based Files, and American Indian Area-based Files.
- Compare the geographies (the Layer column) which are available in the Nation-Based Files category to those available in the State-Based Files category.
What files are available for a state that are not available for the whole nation? Can you think of reasons why these are not available as a single national file?
- Now, compare the State-Based Files category to the County-Based Files category.
What files available at the state level are also available at the county-level? Once again, share your thoughts with your peers.
Geometric Primitives
Like other implementations of the vector data model, MAF/TIGER represents geographic entities using geometric primitives including nodes (point features), edges (linear features), and faces (area features). These are defined and illustrated below.
- Nodes (labeled “N” in the illustration below) are "0-dimensional," consisting only of a single pair of latitude and longitude coordinates.
- Nodes N21-23 are isolated nodes. That is, they are not end points of edges.
- Edges (labeled “E” in the illustration below) are 1-dimensional linear primitives used to represent streets, railroads, pipelines, and rivers.
- The end points of an edge are called connecting nodes.
- Each edge is assigned a direction, denoted by the arrowheads. The directionality of the edge allows the designation of a Start Node and an End Node. The Start Node of edge E12 below is N9, and the End Node is N6.
- An edge may have intermediate points called vertices that define its shape.
- Faces (labeled “F” in Figure 4.4.1, below) are the 2-dimensional geometric primitives used to represent entities like blocks, counties, and voting districts. A face is a polygon bounded by edges.
- The directionality of an edge also allows left and right faces to be designated. Face F1 is on the left of edge E12 and face F2 is to the right.

Geometric Accuracy
Until recently, the geometric accuracy of the vector features encoded in TIGER was notoriously poor (see figure below). How poor? Through 2003, the TIGER/Line metadata stated that
Coordinates in the TIGER/Line files have six implied decimal places, but the positional accuracy of these coordinates is not as great as the six decimal places suggest. The positional accuracy varies with the source materials used, but generally, the information is no better than the established National Map Accuracy standards for 1:100,000-scale maps from the U.S. Geological Survey (Census Bureau 2003).
Try This!
Having performed scale calculations in Chapter 2, you should be able to calculate the magnitude of error (ground distance) associated with 1:100,000-scale topographic maps. Recall that the allowed error for USGS topographic maps at scales of 1:20,000 or smaller is 1/50 inch (see the nationalmap standards pdf).

Accuracy Improvement
Starting in 2002, in preparation for the 2010 census, the Census Bureau commissioned a six-year, $200 million MAF/TIGER Accuracy Improvement Project (MTAIP). One objective of the effort was to use GPS to capture accurate geographic coordinates for every household in the MAF. Another objective was to improve the accuracy of TIGER's road/path features. The project aimed to adjust the geometry of street networks to align within 7.6 meters of street intersections observed in orthoimages or measured using GPS. The corrected streets are necessary not just for mapping, but for accurate geocoding. Because streets often form the boundaries of census areas, it is essential that accurate household locations are associated with accurate street networks.
MTAIP integrated over 2,000 source files submitted by state, tribal, county, and local governments. Contractors used survey-grade GPS to evaluate the accuracy of a random sample of street centerline intersections of the integrated source files. The evaluation confirmed that most but not all features in the spatial database equal or exceed the 7.6-meter target. Uniform accuracy wasn’t possible due to the diversity of local source materials used, though this accuracy is the standard in the "All Lines" Shapefile extracts. The geometric accuracy of particular feature classes included in particular shapefiles is documented in the metadata associated with that shapefile extract.
MTAIP was completed in 2008. In conjunction with the continuous American Community Survey and other census operations, corrections and updates are now ongoing. TIGER/Line Shapefile updates are now released annually.

4. Shapefiles
Since 2007, TIGER/Line extracts from the MAF/TIGER database have been distributed in shapefile format. Esri introduced shapefiles in the early 1990s as the native digital vector data format of its ArcView software product. The shapefile format is proprietary but open; its technical specifications are published and can be implemented and used freely. Largely as a result of ArcView’s popularity, shapefile has become a de facto standard for creation and interchange of vector geospatial data. The Census Bureau’s adoption of Shapefile as a distribution format is therefore consistent with its overall strategy of conformance with mainstream information technology practices.
Elements of a Shapefile Data Set
The first thing GIS pros need to know about shapefiles is that every shapefile data set includes a minimum of three files. One of the three required files stores the geometry of the digital features as sets of vector coordinates. A second required file holds an index that, much like the index in a book, allows quick access to the spatial features and therefore speeds processing of a given operation involving a subset of features. The third required file stores attribute data in dBASE© format, one of the earliest and most widely-used digital database management system formats. All of the files that make up a Shapefile data set have the same root or prefix name, followed by a three-letter suffix or file extension. The list below shows the names of the three required files making up a shapefile data set named “counties.” Take note of the file extensions:
- counties.shp: the main shape file, containing vector coordinate data
- counties.shx: the index file
- counties.dbf: the dBASE table
Esri lists twelve additional optional files, and practitioners are able to include still others. Two of the most important optional files are the “.prj” file, which includes the coordinate system definition, and “.xml”, which stores metadata. (Why do you suppose that something as essential as a coordinate system definition is considered “optional”?)
Try This!
Downloading and viewing a TIGER/Line Shapefile
In this Try This! (the second of 3 dealing with TIGER/Line Shapefiles), you will download a TIGER/Line Shapefile dataset, investigate the file structure of a typical Esri shapefile, and view it in GIS software.
You can use a free software application called Global Mapper (originally known as dlgv32 Pro) to investigate TIGER/Line shapefiles. Originally developed by the staff of the USGS Mapping Division at Rolla, Missouri as a data viewer for USGS data, Global Mapper has since been commercialized but is available in a free trial version. The instructions below will guide you through the process of installing the software and opening the TIGER/Line data.
- Downloading TIGER/Line Shapefiles: You are going to use the 2010 TIGER/Line Shapefiles.
- Return to the 2010 TIGER/Line Shapefiles download page.
- From the Select a layer type pick list, under Features, choose All Lines, and click submit. (You are welcome to download and investigate any TIGER/Line Shapefile(s), but we will use an All Lines dataset in the geocoding Try This later in the chapter, so your downloading one here will make you more familiar with the content.)
- From the All Lines pick list, select a state or territory, and click Submit.
- Select a County from the next pick list that appears, and click Download.
- Save the file to your computer.
The file you download should have a name like tl_2010_42027_edges.zip. The root name of this file, tl_2010_42027_edges in this example, will also be the name of the shapefile dataset. The 42027 is a federal code that represents Pennsylvania (state 42) and Centre County (county 027). The five-digit code in your file name will depend on which state and county you selected. - The data are compressed in a .zip archive. Extract the data to a new named folder in a known location. (Within the file hierarchy that is extracted, there may be a second .zip file that needs to be uncompressed.)
- Investigating the shapefile data set:
- Navigate to within the folder in which you stored your uncompressed TIGER/Line Shapefile dataset.
- Notice the multiple files which make up the shapefile dataset, including:
- tl_2010_42027_edges.shp, containing the vector coordinate data
- tl_2010_42027_edges.shp.xml, containing metadata
- tl_2010_42027_edges.shx, the index file
- tl_2010_42027_edges.dbf, the dBASE file
- tl_2010_42027_edges.prj, containing the projection/spatial reference
- All of the files work in concert to store the necessary components of the Esri shapefile data set. You may be familiar with some of the individual files types. The contents of three of them can be easily viewed. Let's open those three. You can double click on the file and then select "from a list of installed programs,” or you may need to run the suggested application and open the file from within it.
- Open the .dbf file using Microsoft Excel.
Note the typical row-column structure of a flat-file database. Can you find the four columns, or fields, that hold the address range information? Look for LFROMADD, etc. The field name LFROMADD is shorthand for Left From Address. The 10-character length of the field name points up one of the constraints of the dBASE format -- field names are limited to 10 characters. - Open the .xml file using your web browser.
You should see the metadata information bracketed by tags contained within directional brackets < >. XML stands for Extensible Markup Language and is a common set of rules for encoding documents. Can you locate the portion of the document having to do with horizontal spatial accuracy? (Spatial accuracy metadata is available when you've chosen the All Lines file as your candidate shapefile.) - Open the .prj file using Notepad, or any vanilla text editor.
There are five pieces of information in this file, separated by commas. What are they? They should reinforce some of what you learned in Chapter 2 regarding what defines a geographic coordinate system. - The .shp and .shx files are proprietary and specific to the functionality of the shapefile data set.
- Open the .dbf file using Microsoft Excel.
- Note that one should not alter the contents of any of these files with any application other than a GIS program that is designed for that task.
- Viewing the shapefile dataset in Global Mapper:
- Download and install the Global Mapper software:
- Navigate to the Blue Marble Global Mapper site.
- Download the trial version of the software.
- Double-click on the setup file you downloaded to install the program.
- Launch the Global Mapper program.
- After opening the Global Mapper software, choose Open Data File(s)... under the File menu, or click the "Open Your Own Data Files" button in the center of the window. Navigate to the extracted shapefile dataset you downloaded above and open it. (Remember, your complete shapefile data set will have a name similar to tl_2010_42027_edges. It will show up in the Open dialog with a .shp extension.)
- You should be able to see all of the line features (the edges, from the MAF/TIGER database) contained in your county. If you are using the newest version of Global Mapper, you should be able to discern roads from rivers/streams from administrative boundaries, etc. In older versions of the application, the default view showed all line features in a single color and line weight, so the user needed to use the symbolization tools to make the different classes of features distinguishable.
What do you think has to be understood by the mapping application to allow it to automatically symbolize features differently?
- Download and install the Global Mapper software:
Shapefile Primitives
A single shapefile data set can contain one of three types of spatial data primitives, or features – points, lines or polygons (areas). The technical specification defines these as follows:
- Points: A point consists of a pair of double-precision coordinates in the order X,Y.
- Lines: More specifically a polyline, is an ordered set of points, or vertices, that consists of one or more parts. A part is a connected sequence of two or more points. Parts may or may not be connected to one another. Parts may or may not intersect one another.
- Polygons: A polygon consists of one or more rings. A ring is a connected sequence of four or more points, or vertices, that form a closed, non-self-intersecting loop.
- Other: M (measured; route data) and Z (3D; vertical datum) versions of point, polyline, and polygon Shapefile data sets can be created, but are not included in the TIGER/Line Shapefile extracts.
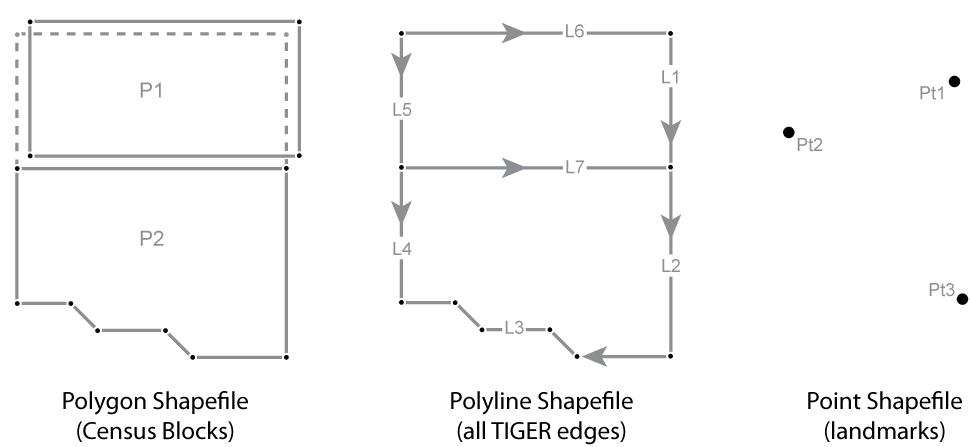
At left in the figure above, a polygon Shapefile data set holds the Census blocks in which the edges from the MAF/TIGER database have been combined to form two distinct polygons, P1 and P2. The diagram shows the two polygons separated to emphasize the fact that what is the single E12 edge in the MAF/TIGER database (see the Figure 4.4.1 on page 4) is now present in each of the Census block polygon features.
In the middle of the illustration, above, a polyline Shapefile data set holds seven line features (L1-7) that correspond to the seven edges in the MAF/TIGER database. The directionality of the line features that represent streets corresponds to address range attributes in the associated dBASE© table. Vertices define the shape of a polygon or a line, and the Start and End Nodes from the MAF/TIGER database are now First and Last Vertices.
Finally, at right in the illustration above, a point Shapefile data set holds the three isolated nodes from the MAF/TIGER database.

5. Topology
Topology is different from topography. (You’d be surprised how often these terms get mixed up.) In Chapter 2, you read about the various ways that absolute positions of features can be specified in a coordinate system, and how those coordinates can be projected or otherwise transformed. Topology refers to the relative positions of spatial features. Topological relations among features — such as containment, connectivity, and adjacency—don’t change when a dataset is transformed. For example, if an isolated node (representing a household) is located inside a face (representing a congressional district) in the MAF/TIGER database, you can count on it remaining inside that face no matter how you might project, rubber-sheet, or otherwise transform the data. Topology is vitally important to the Census Bureau, whose constitutional mandate is to accurately associate population counts and characteristics with political districts and other geographic areas.
As David Galdi (2005) explains in his white paper “Spatial Data Storage and Topology in the Redesigned MAF/TIGER System,” the “TI” in TIGER stands for “Topologically Integrated.” This means that the various features represented in the MAF/TIGER database—such as streets, waterways, boundaries, and landmarks (but not elevation!)—are not encoded on separate “layers.” Instead, features are made up of a small set of geometric primitives—including 0-dimensional nodes and vertices, 1-dimensional edges, and 2-dimensional faces—without redundancy. That means that where a waterway coincides with a boundary, for instance, MAF/TIGER represents them both with one set of edges, nodes, and vertices. The attributes associated with the geometric primitives allow database operators to retrieve feature sets efficiently with simple spatial queries. The separate feature-specific TIGER/Line Shapefiles published at the county level (such as point landmarks, hydrography, Census block boundaries, and the "All Lines" file you are using in the multi-part "Try This") were extracted from the MAF/TIGER database in that way. Notice, however, that when you examine a hydrography shapefile and a boundary shapefile, you will see redundant line segments where the features coincide. That fact confirms that TIGER/Line Shapefiles, unlike the MAF/TIGER database itself, are not topologically integrated. Desktop computers are now powerful enough to calculate topology “on the fly” from shapefiles or other non-topological data sets. However, the large batch processes performed by the Census Bureau still benefit from the MAF/TIGER database’s persistent topology.
MAF/TIGER’s topological data structure also benefits the Census Bureau by allowing it to automate error-checking processes. By definition, features in the TIGER/Line files conform to a set of topological rules (Galdi 2005):
- Every edge must be bounded by two nodes (start and end nodes).
- Every edge has a left and right face.
- Every face has a closed boundary consisting of an alternating sequence of nodes and edges.
- There is an alternating closed sequence of edges and faces around every node.
- Edges do not intersect each other, except at nodes.
Compliance with these topological rules is an aspect of data quality called logical consistency. In addition, the boundaries of geographic areas that are related hierarchically—such as blocks, block groups, tracts, and counties—are represented with common, non-redundant edges. Features that do not conform to the topological rules can be identified automatically, and corrected by the Census geographers who edit the database. Given that the MAF/TIGER database covers the entire U.S. and its territories, and includes many millions of primitives, the ability to identify errors in the database efficiently is crucial.
So how does topology help the Census Bureau assure the accuracy of population data needed for reapportionment and redistricting? To do so, the Bureau must aggregate counts and characteristics to various geographic areas, including blocks, tracts, and voting districts. This involves a process called “address matching” or “address geocoding” in which data collected by household is assigned a topologically-correct geographic location. The following pages explain how that works.

6. Geocoding
Geocoding is the process used to convert location codes, such as street addresses or postal codes, into geographic (or other) coordinates. The terms “address geocoding” and “address mapping” refer to the same process. Geocoding address-referenced population data is one of the Census Bureau’s key responsibilities. However, as you know, it’s also a very popular capability of online mapping and routing services. In addition, geocoding is an essential element of a suite of techniques that are becoming known as “business intelligence.” We’ll look at applications like these later in this chapter, but first, let’s consider how the Census Bureau performs address geocoding.
Address Geocoding at the U.S. Census
Prior to the MAF/TIGER modernization project that led up to the decennial census of 2010, the TIGER database did not include a complete set of point locations for U.S. households. Lacking point locations, TIGER was designed to support address geocoding by approximation. As illustrated below in Figure 4.7.1, the pre-modernization TIGER database included address range attributes for the edges that represent streets. Address range attributes were also included in the TIGER/Line files extracted from TIGER. Coupled with the Start and End nodes bounding each edge, address ranges enable users to estimate locations of household addresses.

Here’s how it works. The diagram above highlights an edge that represents a one-block segment of Oak Avenue. The edge is bounded by two nodes, labeled "Start" and "End." A corresponding record in an attribute table includes the unique ID number (0007654320) that identifies the edge, along with starting and ending addresses for the left (FRADDL, TOADDL) and right (FRADDR, TOADDR) sides of Oak Avenue. Note also that the address ranges include potential addresses, not just existing ones. This is to make sure that the ranges will remain valid as new buildings are constructed along the street.
A common geocoding error occurs when Start and End designations are assigned to the wrong connecting nodes. You may have read in Galdi’s (2005) white paper “Spatial Data Storage and Topology in the Redesigned MAF/TIGER System,” that in MAF/TIGER, “an arbitrary direction is assigned to each edge, allowing designation of one of the nodes as the Start Node, and the other as the End Node” (p. 3). If an edge’s “direction” happens not to correspond with its associated address ranges, a household location may be placed on the wrong side of a street.
Although many local governments in the U.S. have developed their own GIS “land bases” with greater geometric accuracy than pre-modernization TIGER/Line files, similar address geocoding errors still occur. Kathryn Robertson, a GIS Technician with the City of Independence, Missouri pointed out how important it is that Start (or "From") nodes and End (or "To") nodes correspond with the low and high addresses in address ranges. "I learned this the hard way," she wrote, "geocoding all 5,768 segments for the city of Independence and getting some segments backward. When address matching was done, the locations were not correct. Therefore, I had to go back and look at the direction of my segments. I had a rule of thumb, all east-west streets were to start from west and go east; all north-south streets were to start from the south and go north" (personal communication).
Although this may have been a sensible strategy for the City of Independence, can you imagine a situation in which Kathryn’s rule-of-thumb might not work for another municipality?
After MAF/TIGER Modernization
If TIGER had included accurate coordinate locations for every household, and correspondingly accurate streets and administrative boundaries, geocoding census data would be simple and less error-prone. Many local governments digitize locations of individual housing units when they build GIS land bases for property tax assessment, E-911 dispatch, and other purposes. The MAF/TIGER modernization project begun in 2002 aimed to accomplish this for the entire nationwide TIGER database in time for the 2010 census. The illustration below in Figure 4.7.2 shows the intended result of the modernization project, including properly aligned streets, shorelines, and individual household locations, shown here in relation to an orthorectified aerial image.
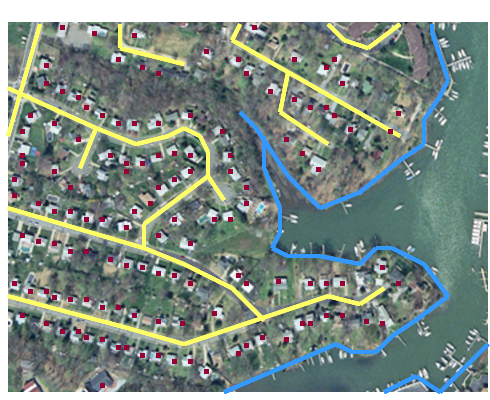
The modernized MAF/TIGER database described by Galdi (2005) is now in use, including precise geographic locations of over 100 million household units. However, because household locations are considered confidential, users of TIGER/Line Shapefiles extracted from the MAF/TIGER database still must rely upon address geocoding using address ranges.
Leveraging TIGER/Line data for Private Enterprise
Launched in 1996, MapQuest was one of the earliest online mapping, geocoding and routing services. MapQuest combined the capabilities of two companies: a cartographic design firm with long experience in producing road atlases, “TripTiks” for the American Automobile Association, and other map products, and a start-up company that specialized in custom geocoding applications for business. Initially, MapQuest relied in part on TIGER/Line street data extracted from the pre-modernization TIGER database. MapQuest and other commercial firms were able to build their businesses on TIGER data because of the U.S. government’s wise decision not to restrict its reuse. It’s been said that this decision triggered the rapid growth of the U.S. geospatial industry.
Later on in this chapter, we’ll visit MapQuest and some of its more recent competitors. Next, however, you'll have a chance to see how geocoding is performed using a TIGER/Line data in a GIS.

7. Geocoding with TIGER/Line Shapefiles
Try This!
Geocoding in a GIS
Part 3 of 3 in the TIGER/Line Shapefile Try This! series is not interactive, but instead illustrates how the address ranges encoded in TIGER/Line Shapefiles can be used to pinpoint (more or less!) the geographic locations of street addresses in the U.S.
The process of geocoding a location within a GIS begins with a line dataset (shapefile) with the necessary address range attributes. The following image is an example of the attribute table of a TIGER/Line shapefile.
This shapefile contains over 29,000 road segments in total. Note the names of some of the attributes:
- FULLNAME - The street name of the road segment
- LFROMADD - The address number at the beginning of the road segment on the left side of the street
- LTOADD - The address number at the end of the road segment on the left side of the street
- RFROMADD - The address number at the beginning of the road segment on the right side of the street
- RTOADD - The address number at the end of the road segment on the right side of the street
- ZIPL - The ZIP code area that is present to the left side of the road segment
- ZIPR - The ZIP code area that is present to the right side of the street
Next, the GIS software needs to know which of these attributes contains each piece of the necessary address range information. Some shapefiles use different names for their attributes, so the GIS can't always know which attribute contains the Right-Side-From-Address information, for example. In ArcGIS, for example, something called a Locator is configured that maps the attributes in the shapefile to the corresponding piece of necessary address information. The image below illustrates what this mapping looks like:
We are now ready to find a location by searching for a street address! Let's geocode the location for "1971 Fairwood Lane, 16803".
When an address is specified, the GIS queries the attribute table to find rows with a matching street name in the correct ZIP code. Also, the particular segment of the street that contains the address number is identified. Figure 4.8.3 shows the corresponding selection in the attribute table:
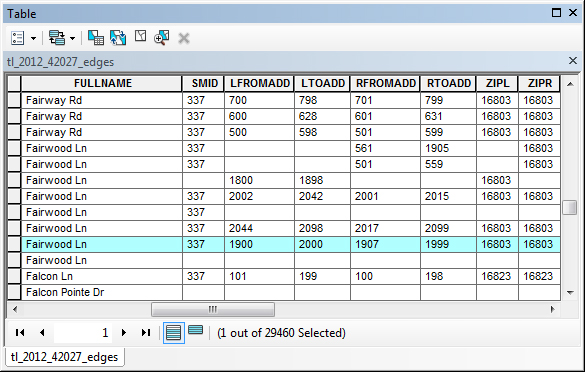
Figure 4.8.4 shows the corresponding road segment highlighted on a map. The To and From address values for the road segment have been added so you can see the range of addresses.
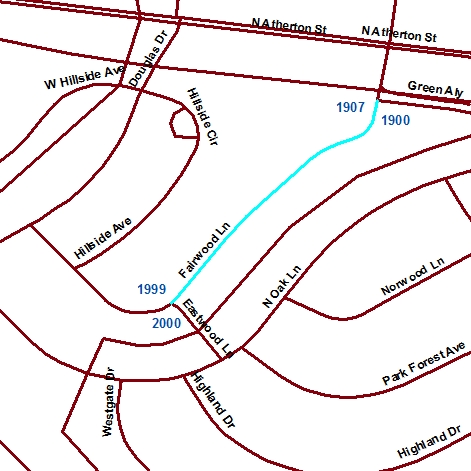
Finally, the GIS interpolates where along the road segment the value of 1971 occurs and places it on the appropriate side of the street based on the even/odd values indicated in the attribute table. Figure 4.8.5 shows the final result of the geocoding process:
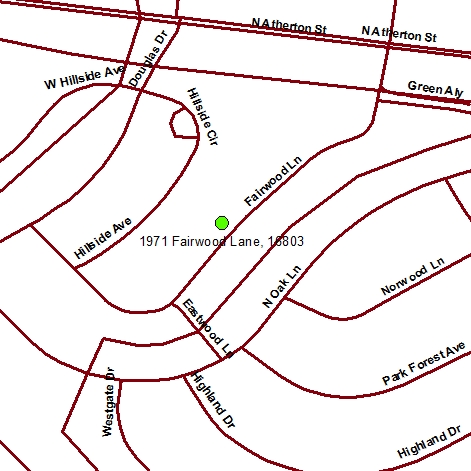
The accuracy of a geocoded location is dependent on a number of factors, including the quality of the line work in a shapefile, the accuracy of the address range attributes of each road segment, and the interpolation performed by the software. As you may see in the following section, different geocoding services may provide different location results due to the particular data and procedures used.

8. Geocoding Online
No doubt you're familiar with one or more popular online mapping services. How well do they do at geocoding the location of a postal address? You can try it out for yourself at several web-based mapping services, including MapQuest.com, Microsoft's Bing Maps, and Tele Atlas/TomTom's Geocode.com (no longer a live site). Tele Atlas, for example, has been a leading manufacturer of digital street data for vehicle navigation systems. To accommodate the routing tasks that navigation systems are called upon to serve, the streets are encoded as vector features whose attributes include address ranges. (In order to submit an address for geocoding at Geocode.com, you have to set up a trial account through their EZ-Locate Interactive web tool or download the EZ-Locate software).

Shown above is the form by which you can geocode an address to a location in a Tele Atlas street database. The result is shown below in Figure 4.9.2.

Let's compare the geocoding capabilities of MapQuest.com to locate the address on an actual map.

The MapQuest.com map from 2013 estimates the address is close to its actual location. Below is a similar MapQuest product created back in 1998. On the older map, the same address is plotted on the opposite side of the street. What do you suppose is wrong with the address range attribute in that case?
On the map from 1998, also note the shapes of the streets. The street shapes in the 2011 map have been improved. The 1998 product seems to have been generated from the 1990 version of the TIGER/Line files, which may have been all that was available for this relatively remote part of the country. Now MapQuest licenses street data from a business partner called NAVTEQ.

The point of this section is to show that geocoding with address ranges involves a process of estimation. The Census Bureau's TIGER/Line Shapefiles, like the commercial street databases produced by Tele Atlas, Navigation Technologies, and other private firms, represent streets as vector line segments. The vector segments are associated with address range attributes, one for the left side of the street, one for the right side. The geocoding process takes a street address as input, finds the line segment that represents the specified street, checks the address ranges to determine the correct side of the street, then estimates a location at the appropriate point between the minimum and maximum address for that segment and assigns an estimated latitude/longitude coordinate to that location. For example, if the minimum address is 401, and the maximum is 421, a geocoding algorithm would locate address 411 at the midpoint of the street segment.
Try This!
Try one of these geocoding services for your address. Then compare the experience, and the result, with Google Maps, launched in 2005. Apply what we've discussed in this chapter to try to explain inaccuracies in your results, if any.

9. Applications beyond the Census Bureau
Two characteristics of MAF/TIGER data, address range attributes and explicit topology, make them, and derivative products, valuable in many contexts. Consequently, firms like NAVTEQ and Tele Atlas (now owned by TomTom) emerged to provide data with similar characteristics as MAF/TIGER, but which are more up-to-date, more detailed, and include additional feature classes. The purpose of the next section is to sketch some of the applications of data similar to MAF/TIGER data beyond the Census Bureau.
Read This
A February 2006 article by Peter Valdes-Dapena in CNNMoney.com describes the work of two NAVTEQ employees. See the link above or search on "where those driving directions really come from."
10. Geocoding Your Customers
Geocoded addresses allow governments and businesses to map where their constituents and customers live and work. Federal, state, and local government agencies know where their constituents live by virtue of censuses, as well as applications for licenses and registrations. Banks, credit card companies, and telecommunications firms are also rich in address-referenced customer data, including purchasing behaviors. Private businesses and services must be more resourceful.
Some retail operations, for example, request addresses or ZIP Codes from customers, or capture address data from checks. Discount and purchasing club cards allow retailers to directly match purchasing behaviors with addresses. Customer addresses can also be harvested from automobile license plates. Business owners pay to record license plate numbers of cars parked in their parking lots or in those of their competitors. Addresses of registered owners can be purchased from organizations that acquire motor vehicle records from state departments of transportation.
Businesses with access to address-referenced customer data, vector street data attributed with address ranges, and GIS software and expertise, can define and analyze the trade areas within which most of their customers live and work. Companies can also focus direct mail advertising campaigns on their own trade areas, or their competitors'. Furthermore, GIS can be used to analyze the socio-economic characteristics of the population within trade areas, enabling businesses to make sure that the products and services they offer meet the needs and preferences of target populations.
Politicians use the same tools to target appearances and campaign promotions.
Try This!
Check out the geocoding system maintained by the Federal Financial Institution's Examination Council. The FFIEC Geocoding system lets users enter a street address and get a census demographic report or a street map (Using Tele Atlas data). The system is intended for use by financial institutions that are covered by the Home Mortgage Disclosure Act (HMDA) and Community Reinvestment Act (CRA) to meet their reporting obligation.

11. Delivering Products and Services
Operations such as mail and package delivery, food and beverage distribution, and emergency medical services need to know not only where their customers are located, but how to deliver products and services to those locations as efficiently as possible. Geographic data products like TIGER/Line Shapefiles are valuable to analysts responsible for prescribing the most efficient delivery routes. The larger and more complex the service areas of such organizations, the more incentive they have to automate their routing procedures.
In its simplest form, routing involves finding the shortest path through a network from an origin to a destination. Although shortest path algorithms were originally implemented in raster frameworks, transportation networks are now typically represented with vector feature data, like TIGER/Line Shapefiles. Street segments are represented as digital line segments each formed by two points, a "start" node and an "end" node. If the nodes are specified within geographic or plane coordinate systems, the distance between them can be calculated readily. Routing procedures sum the lengths of every plausible sequence of line segments that begin and end at the specified locations. The sequence of segments associated with the smallest sum represents the shortest route.
To compare various possible sequences of segments, the data must indicate which line segment follows immediately after another line segment. In other words, the procedure needs to know about the connectivity of features. As discussed earlier, connectivity is an example of a topological relationship. If topology is not encoded in the data product, it can be calculated by the GIS software in which the procedure is coded.

Several online travel planning services, including MapQuest.com and Google Maps, provide routing capabilities. Both take origin and destination addresses as input, and produce optimal routes as output. These services are based on vector feature databases in which street segments are attributed with address ranges, as well as with other data that describe the type and conditions of the roads they represent.

The shortest route is not always the best. In the context of emergency medical services, for example, the fastest route is preferred, even if it entails longer distances than others. To determine fastest routes, additional attribute data must be encoded, such as speed limits, traffic volumes, one way streets, and other characteristics.

Then there are routing problems that involve multiple destinations--a complex special case of routing called the traveling salesman problem. School bus dispatchers, mail and package delivery service managers, and food and beverage distributors all seek to minimize the transportation costs involved in servicing multiple, dispersed destinations. As the number of destinations and the costs of travel increase, the high cost of purchasing up-to-date, properly attributed network data becomes easier to justify.
Try This!
The Georgia Institute of Technology publishes an extensive collection of resources about the Traveling Salesman Problem. Go to this site: http://www.gatech.edu/ and type traveling salesman in the Search slot.

12. Delineating Service Areas
The need to redraw voting district boundaries every ten years was one of the motivations that led the Census Bureau to create its MAF/TIGER database. Like voting districts, many other kinds of service area boundaries need to be revised periodically. School districts are a good example. The state of Massachusetts, for instance, has adopted school districting laws that are similar in effect to the constitutional criteria used to guide congressional redistricting. The Framingham (Massachusetts) School District's Racial Balance Policy once stated that "each elementary and middle school shall enroll a student body that is racially balanced. ... each student body shall include a percentage of minority student, which reflects the system-wide percentage of minority students, plus or minus ten percent. ... The racial balance required by this policy shall be established by redrawing school enrollment areas" (Framingham Public Schools 1998). And bus routes must be redrawn as enrollment area boundaries change.
The Charlotte-Mecklenberg (North Carolina) public school district also used racial balance as a districting criterion (although its policy was subsequently challenged in court). Charlotte-Mecklenberg consists of 133 schools, attended by over 100,000 students, about one-third of whom ride a bus to school every day. District managers are responsible for routing 3,600 bus routes, traveling a total of 82,000 daily miles. A staff of eight routinely uses GIS to manage these tasks. GIS could not be used unless up-to-date, appropriately attributed, and topologically encoded data were available.
Another example of service area analysis is provided by the City of Beaverton, Oregon. In 1997, Beaverton officials realized that 25 percent of the volume of solid waste that was hauled away to landfills consisted of yard waste, such as grass clippings and leaves. Beaverton decided to establish a yard waste recycling program, but it knew that the program would not be successful if residents found it inconvenient to participate. A GIS procedure called allocation was used to partition Beaverton's street network into service areas that minimized the drive time from residents' homes to recycling facilities. Allocation procedures require vector-format data that includes the features, attributes, and topology necessary to calculate travel times from all residences to the nearest facility.

Naturally, private businesses concerned with delivering products and services are keenly interested in service area delineation. The screen capture above shows two trade areas surrounding a retail store location ("Seattle Downtown") in a network database.
Former student Saskia Cohick (Winter 2006), who was then GIS Director for Tioga County, Pennsylvania, contributed another service area problem: "This is a topic that local governments are starting to deal with ... To become Phase 2 wireless capable (that is, capable of finding a cell phone location from a 911 call center within 200 feet of the actual location), county call centers must have a layer called ESZs (Emergency Service Zones). This layer will tell the dispatcher who to send to the emergency (police, fire, medical, etc). The larger problem is to reach an agreement between four fire companies (for example) as to where they do or do not respond."
13. Summary
To fulfill its mission of being the preeminent producer of attribute data about the population and economy of the United States, the U.S. Census Bureau also became an innovative producer of digital geographic data. The Bureau designed its MAF/TIGER database to support automatic geocoding of address-referenced census data, as well as automatic data quality control procedures. The key characteristics of TIGER/Line Shapefiles, including the use of vector features to represent geographic entities, and address range attributes to enable address geocoding, are now common features of proprietary geographic databases used for trade area analysis, districting, routing, and allocation.

14. Bibliography
Chapter 5: Land Surveying and GPS
1. Overview
As you recall from Chapter 1, geographic data represent spatial locations and non-spatial attributes measured at certain times. We defined "feature" as a set of positions that specifies the location and extent of an entity. Positions, then, are a fundamental element of geographic data. Like the letters that make up these words, positions are the building blocks from which features are constructed. A property boundary, for example, is made up of a set of positions connected by line segments.
In theory, a single position is a "0-dimensional" feature: an infinitesimally small point from which 1-dimensional, 2-dimensional, and 3-dimensional features (lines, areas, and volumes) are formed. In practice, positions occupy 2- or 3-dimensional areas as a result of the limited resolution of measurement technologies and the limited precision of location coordinates. Resolution and precision are two aspects of data quality. This chapter explores the technologies and procedures used to produce positional data, and the factors that determine its quality.
Objectives
Students who successfully complete Chapter 5 should be able to:
- identify and define the key aspects of data quality, including resolution, precision, and accuracy;
- list and explain the procedures land surveyors use to produce positional data, including traversing, triangulation, and trilateration;
- calculate plane coordinates by open traverse;
- calculate elevations by leveling;
- explain how radio signals broadcast by Global Positioning System satellites are used to calculate positions on the surface of the Earth;
- state the kinds and magnitude of error associated with uncorrected GPS positioning; and
- identify and explain methods used to improve the accuracy of GPS positioning.
"Try This!" Activities
Take a minute to complete any of the Try This activities that you encounter throughout the chapter. These are fun, thought-provoking exercises to help you better understand the ideas presented in the chapter.

2. Geospatial Data Quality
Quality is a characteristic of comparable things that allows us to decide that one thing is better than another. In the context of geographic data, the ultimate standard of quality is the degree to which a data set is fit for use in a particular application. That standard is called validity. The standard varies from one application to another. In general, however, the key criteria are how much error is present in a data set, and how much error is acceptable.
Some degree of error is always present in all three components of geographic data: features, attributes, and time. Perfect data would fully describe the location, extent, and characteristics of phenomena exactly as they occur at every moment. Like the proverbial 1:1 scale map, however, perfect data would be too large, and too detailed to be of any practical use. Not to mention impossibly expensive to create in the first place!
3. Error and Uncertainty
Positions are the products of measurements. All measurements contain some degree of error. Errors are introduced in the original act of measuring locations on the Earth surface. Errors are also introduced when second- and third-generation data is produced, say, by scanning or digitizing a paper map.
In general, there are three sources of error in measurement: human beings, the environment in which they work, and the measurement instruments they use.
Human errors include mistakes, such as reading an instrument incorrectly, and judgments. Judgment becomes a factor when the phenomenon that is being measured is not directly observable (like an aquifer), or has ambiguous boundaries (like a soil unit).
Environmental characteristics, such as variations in temperature, gravity, and magnetic declination, also result in measurement errors.
Instrument errors follow from the fact that space is continuous. There is no limit to how precisely a position can be specified. Measurements, however, can be only so precise. No matter what instrument, there is always a limit to how small a difference is detectable. That limit is called resolution.
Figure 5.4.1, below, shows the same position (the point in the center of the bullseye) measured by two instruments. The two grid patterns represent the smallest objects that can be detected by the instruments. The pattern at left represents a higher-resolution instrument.

The resolution of an instrument affects the precision of measurements taken with it. In the illustration below, the measurement at left, which was taken with the higher-resolution instrument, is more precise than the measurement at right. In digital form, the more precise measurement would be represented with additional decimal places. For example, a position specified with the UTM coordinates 500,000. meters East and 5,000,000. meters North is actually an area 1 meter square. A more precise specification would be 500,000.001 meters East and 5,000,000.001 meters North, which locates the position within an area 1 millimeter square. You can think of the area as a zone of uncertainty within which, somewhere, the theoretically infinitesimal point location exists. Uncertainty is inherent in geospatial data.
Precision takes on a slightly different meaning when it is used to refer to a number of repeated measurements. In the Figure 5.4.3, below, there is less variance among the nine measurements at left than there is among the nine measurements at right. The set of measurements at left is said to be more precise.

Hopefully, you have noticed that resolution and precision are independent from accuracy. As shown below, accuracy simply means how closely a measurement corresponds to an actual value.

I mentioned the U.S. Geological Survey's National Map Accuracy Standard in Chapter 2. In regard to topographic maps, the Standard warrants that 90 percent of well-defined points tested will be within a certain tolerance of their actual positions. Another way to specify the accuracy of an entire spatial database is to calculate the average difference between many measured positions and actual positions. The statistic is called the root mean square error (RMSE) of a data set.
4. Systematic vs. Random Errors
The diagram below illustrates the distinction between systematic and random errors. Systematic errors tend to be consistent in magnitude and/or direction. If the magnitude and direction of the error is known, accuracy can be improved by additive or proportional corrections. Additive correction involves adding or subtracting a constant adjustment factor to each measurement; proportional correction involves multiplying the measurement(s) by a constant.
Unlike systematic errors, random errors vary in magnitude and direction. It is possible to calculate the average of a set of measured positions, however, and that average is likely to be more accurate than most of the measurements.

In the sections that follow, we compare the accuracy and sources of error of two important positioning technologies: land surveying and the Global Positioning System.
5. Survey Control
Geographic positions are specified relative to a fixed reference. Positions on the globe, for instance, may be specified in terms of angles relative to the center of the Earth, the equator, and the prime meridian. Positions in plane coordinate grids are specified as distances from the origin of the coordinate system. Elevations are expressed as distances above or below a vertical datum such as mean sea level, or an ellipsoid such as GRS 80 or WGS 84, or a geoid.
Land surveyors measure horizontal positions in geographic or plane coordinate systems relative to previously surveyed positions called control points. In the U.S., the National Geodetic Survey (NGS) maintains a National Spatial Reference System (NSRS) that consists of approximately 300,000 horizontal and 600,000 vertical control stations (Doyle,1994). Coordinates associated with horizontal control points are referenced to NAD 83; elevations are relative to NAVD 88. In a Chapter 2 activity, you may have retrieved one of the datasheets that NGS maintains for every NSRS control point, along with more than a million other points submitted by professional surveyors.

In 1988, NGS established four orders of control point accuracy, which are outlined in the table below. The minimum accuracy for each order is expressed in relation to the horizontal distance separating two control points of the same order. For example, if you start at a control point of order AA and measure a 500 km distance, the length of the line should be accurate to within 3 mm base error, plus or minus 5 mm line length error (500,000,000 mm × 0.01 parts per million).
| Order | Survey activities |
Maximum base error (95% confidence limit) |
Maximum Line-length dependent error (95% confidence limit) |
|---|---|---|---|
| AA | Global-regional dynamics; deformation measurements | 3 mm |
1:100,000,000
(0.01 ppm)
|
| A | NSRS primary networks | 5 mm | 1:10,000,000 (0.1 ppm) |
| B | NSRS secondary networks; high-precision engineering surveys | 8 mm | 1:1,000,000 (1 ppm) |
| C | NSRS terrestrial; dependent control surveys for mapping, land information, property, and engineering requirements | 1st: 1.0 cm 2nd-I: 2.0 cm 2nd-II: 3.0 cm 3rd: 5.0 cm |
1st: 1:100,000 2nd-I: 1:50,000 2nd-II: 1:20,000 3rd: 1:10,000 |
Doyle (1994) points out that horizontal and vertical reference systems coincide by less than ten percent. This is because
....horizontal stations were often located on high mountains or hilltops to decrease the need to construct observation towers usually required to provide line-of-sight for triangulation, traverse and trilateration measurements. Vertical control points however, were established by the technique of spirit leveling which is more suited to being conducted along gradual slopes such as roads and railways that seldom scale mountain tops. (Doyle, 2002, p. 1)
You might wonder how a control network gets started. If positions are measured relative to other positions, what is the first position measured relative to? The answer is: the stars. Before reliable timepieces were available, astronomers were able to determine longitude only by careful observation of recurring celestial events, such as eclipses of the moons of Jupiter. Nowadays, geodesists produce extremely precise positional data by analyzing radio waves emitted by distant stars. Once a control network is established, however, surveyors produce positions using instruments that measure angles and distances between locations on the Earth's surface.
6. Measuring Angles
Angles can be measured with a magnetic compass, of course. Unfortunately, the Earth's magnetic field does not yield the most reliable measurements. The magnetic poles are not aligned with the planet's axis of rotation (an effect called magnetic declination), and they tend to change location over time. Local magnetic anomalies caused by magnetized rocks in the Earth's crust and other geomagnetic fields make matters worse.
For these reasons, land surveyors rely on transits (or their more modern equivalents, called theodolites) to measure angles. A transit consists of a telescope for seeing distant target objects, two measurement wheels that work like protractors for reading horizontal and vertical angles, and bubble levels to ensure that the angles are true. A theodolite is essentially the same instrument, except that some mechanical parts are replaced with electronics.

Surveyors express angles in several ways. When specifying directions, as is done in the preparation of a property survey, angles may be specified as bearings or azimuths. A bearing is an angle less than 90° within a quadrant defined by the cardinal directions. An azimuth is an angle between 0° and 360° measured clockwise from North. "South 45° East" and "135°" are the same direction expressed as a bearing and as an azimuth. An interior angle, by contrast, is an angle measured between two lines of sight, or between two legs of a traverse (described later in this chapter).

In the U.S., professional organizations like the American Congress on Surveying and Mapping, the American Land Title Association, the National Society of Professional Surveyors, and others, recommend minimum accuracy standards for angle and distance measurements. For example, as Steve Henderson (personal communication, Fall 2000, updated July 2010) points out, the Alabama Society of Professional Land Surveyors recommends that errors in angle measurements in "commercial/high risk" surveys be no greater than 15 seconds times the square root of the number of angles measured.
To achieve this level of accuracy, surveyors must overcome errors caused by faulty instrument calibration; wind, temperature, and soft ground; and human errors, including misplacing the instrument and misreading the measurement wheels. In practice, surveyors produce accurate data by taking repeated measurements and averaging the results.
7. Measuring Distances
To measure distances, land surveyors once used 100-foot long metal tapes that are graduated in hundredths of a foot. (This is the technique I learned as a student in a surveying class at the University of Wisconsin in the early 1980s. The picture shown below is slightly earlier.) Distances along slopes are measured in short horizontal segments. Skilled surveyors can achieve accuracies of up to one part in 10,000 (1 centimeter error for every 100 meters distance). Sources of error include flaws in the tape itself, such as kinks; variations in tape length due to extremes in temperature; and human errors such as inconsistent pull, allowing the tape to stray from the horizontal plane, and incorrect readings.

Since the 1980s, electronic distance measurement (EDM) devices have allowed surveyors to measure distances more accurately and more efficiently than they can with tapes. To measure the horizontal distance between two points, one surveyor uses an EDM instrument to shoot an energy wave toward a reflector held by the second surveyor. The EDM records the elapsed time between the wave's emission and its return from the reflector. It then calculates distance as a function of the elapsed time. Typical short-range EDMs can be used to measure distances as great as 5 kilometers at accuracies up to one part in 20,000, twice as accurate as taping.

Instruments called total stations combine electronic distance measurement and the angle measuring capabilities of theodolites in one unit. Next, we consider how these instruments are used to measure horizontal positions in relation to established control networks.
8. Horizontal Positions
Surveyors have developed distinct methods, based on separate control networks, for measuring horizontal and vertical positions. In this context, a horizontal position is the location of a point relative to two axes: the equator and the prime meridian on the globe, or x and y axes in a plane coordinate system. Control points tie coordinate systems to actual locations on the ground; they are the physical manifestations of horizontal datums. In the following pages, we review two techniques that surveyors use to create and extend control networks (triangulation and trilateration) and two other techniques used to measure positions relative to control points (open and closed traverses).
9. Traverse
Surveyors typically measure positions in series. Starting at control points, they measure angles and distances to new locations and use trigonometry to calculate positions in a plane coordinate system. Measuring a series of positions in this way is known as "running a traverse." A traverse that begins and ends at different locations is called an open traverse.

For example, say the UTM coordinates of point A in Figure 5.10.1 are 500,000.00 E and 5,000,000.00 N. The distance between points A and P, measured with a steel tape or an EDM, is 2,828.40 meters. The azimuth of the line AP, measured with a transit or theodolite, is 45º. Using these two measurements, the UTM coordinates of point P can be calculated as follows:
XP = 500,000.00 + (2,828.40 × sin 45°) = 501,999.98
YP = 5,000,000.00 + (2,828.40 × cos 45°) = 5,001,999.98
A traverse that begins and ends at the same point, or at two different but known points, is called a closed traverse. Measurement errors in a closed traverse can be quantified by summing the interior angles of the polygon formed by the traverse. The accuracy of a single angle measurement cannot be known, but since the sum of the interior angles of a polygon is always (n-2) × 180, it's possible to evaluate the traverse as a whole, and to distribute the accumulated errors among all the interior angles.
Errors produced in an open traverse, one that does not end where it started, cannot be assessed or corrected. The only way to assess the accuracy of an open traverse is to measure distances and angles repeatedly, forward and backward, and to average the results of calculations. Because repeated measurements are costly, other surveying techniques that enable surveyors to calculate and account for measurement error are preferred over open traverses for most applications.
10. Triangulation
Closed traverses yield adequate accuracy for property boundary surveys, provided that an established control point is nearby. Surveyors conduct control surveys to extend and densify horizontal control networks. Before survey-grade satellite positioning was available, the most common technique for conducting control surveys was triangulation.

Using a total station equipped with an electronic distance measurement device, the control survey team commences by measuring the azimuth alpha, and the baseline distance AB. These two measurements enable the survey team to calculate position B as in an open traverse. Before geodetic-grade GPS became available, the accuracy of the calculated position B may have been evaluated by astronomical observation.

The surveyors next measure the interior angles CAB, ABC, and BCA at point A, B, and C. Knowing the interior angles and the baseline length, the trigonometric "law of sines" can then be used to calculate the lengths of any other side. Knowing these dimensions, surveyors can fix the position of point C.

Having measured three interior angles and the length of one side of triangle ABC, the control survey team can calculate the length of side BC. This calculated length then serves as a baseline for triangle BDC. Triangulation is thus used to extend control networks, point by point and triangle by triangle.

11. Trilateration
Trilateration is an alternative to triangulation that relies upon distance measurements only. Electronic distance measurement technologies make trilateration a cost-effective positioning technique for control surveys. Not only is it used by land surveyors, trilateration is also used to determine location coordinates with Global Positioning System satellites and receivers.

Trilateration networks commence the same way as triangulation nets. If only one existing control point is available, a second point (B) is established by open traverse. Using a total station equipped with an electronic distance measurement device, the survey team measures the azimuth α and baseline distance AB. The total station operator may set up her instrument over point A, while her assistant holds a reflector mounted on a shoulder-high pole as steadily as he can over point B. Depending on the requirements of the control survey, the accuracy of the calculated position B may be confirmed by astronomical observation.

Next, the survey team uses the electronic distance measurement feature of the total station to measure the distances AC and BC. Both forward and backward measurements are taken. After the measurements are reduced from slope distances to horizontal distances, the law of cosines can be employed to calculate interior angles, and the coordinates of position C can be fixed. The accuracy of the fix is then checked by plotting triangle ABC and evaluating the error of closure.

Next, the trilateration network is extended by measuring the distances CD and BD, and fixing point D in a plane coordinate system.


12. Vertical Positions
A vertical position is the height of a point relative to some reference surface, such as mean sea level, a geoid, or an ellipsoid. The roughly 600,000 vertical control points in the U.S. National Spatial Reference System (NSRS) are referenced to the North American Vertical Datum of 1988 (NAVD 88). Surveyors created the National Geodetic Vertical Datum of 1929 (NGVD 29, the predecessor to NAVD 88), by calculating the average height of the sea at all stages of the tide at 26 tidal stations over 19 years. Then they extended the control network inland using a surveying technique called leveling. Leveling is still a cost-effective way to produce elevation data with sub-meter accuracy.

The illustration above shows a leveling crew at work. The fellow under the umbrella is peering through the telescope of a leveling instrument. Before taking any measurements, the surveyor made sure that the telescope was positioned midway between a known elevation point and the target point. Once the instrument was properly leveled, he focused the telescope crosshairs on a height marking on the rod held by the fellow on the right side of the picture. The chap down on one knee is noting in a field book the height measurement called out by the telescope operator.

Leveling is still a cost-effective way to produce elevation data with sub-meter accuracy. A modern leveling instrument is shown in Figure 5.13.2, above. Figure 5.13.3 illustrates the technique called differential leveling.

This diagram illustrates differential leveling. A leveling instrument is positioned midway between a point at which the ground elevation is known (point A) and a point whose elevation is to be measured (B). The height of the instrument above the datum elevation is HI. The surveyor first reads a backsight measurement (BS) off of a leveling rod held by his trusty assistant over the benchmark at A. The height of the instrument can be calculated as the sum of the known elevation at the benchmark (ZA) and the backsight height (BS). The assistant then moves the rod to point B. The surveyor rotates the telescope 180°, then reads a foresight (FS) off the rod at B. The elevation at B (ZB) can then be calculated as the difference between the height of the instrument (HI) and the foresight height (FS).
Former student, Henry Whitbeck, (personal communication, Fall 2000) points out that surveyors also use total stations to measure vertical angles and distances between fixed points (prisms mounted upon tripods at fixed heights), and then calculate elevations by trigonometric leveling.
Heights
Surveyors use the term height as a synonym for elevation. There are several different ways to measure heights. A properly-oriented level defines a line parallel to the geoid surface at that point (Van Sickle, 2001). An elevation above the geoid is called an orthometric height. However, GPS receivers cannot produce orthometric heights directly. Instead, GPS produces heights relative to the WGS 84 ellipsoid. Elevations produced with GPS are therefore called ellipsoidal (or geodetic) heights.

13. Global Positioning System

The Global Positioning System (GPS) employs trilateration to calculate the coordinates of positions at or near the Earth's surface. Trilateration refers to the trigonometric law by which the interior angles of a triangle can be determined if the lengths of all three triangle sides are known. GPS extends this principle to three dimensions.
A GPS receiver can fix its latitude and longitude by calculating its distance from three or more Earth-orbiting satellites, whose positions in space and time are known. If four or more satellites are within the receiver's "horizon," the receiver can also calculate its elevation and even its velocity. The U.S. Department of Defense created the Global Positioning System as an aid to navigation. Since it was declared fully operational in 1994, GPS positioning has been used for everything from tracking delivery vehicles, to tracking the minute movements of the tectonic plates that make up the Earth's crust, to tracking the movements of human beings. In addition to the so-called user segment made up of the GPS receivers and people who use them to measure positions, the system consists of two other components: a space segment and a control segment. It took about $10 billion to build over 16 years.
Russia maintains a similar positioning satellite system called GLONASS. Member nations of the European Union are in the process of deploying a comparable system of their own, called Galileo. The first experimental GIOVE-A satellite began transmitting Galileo signals in January 2006. The goal of the Galileo project is a constellation of 30 navigation satellites by 2020. If the engineers and politicians succeed in making Galileo, GLONASS, and the U.S. Global Positioning System interoperable, as currently seems likely, the result will be a Global Navigation Satellite System (GNSS) that provides more than twice the signal-in-space resource that is available with GPS alone. The Chinese began work on their own system, called Beidou, in 2000. At the end of 2011, they had ten satellites in orbit, serving just China, with the goal being a global system of 35 satellites by 2020.
In this section you will learn to:
- Explain how radio signals broadcast by Global Positioning System satellites are used to calculate positions on the surface of the Earth; and
- Describe the functions of the space, control, and user segments of the Global Positioning System.
14. Space Segment
The space segment of the Global Positioning System currently consists of approximately 30 active and spare NAVSTAR satellites (new satellites are launched periodically, and old ones are decommissioned). "NAVSTAR" stands for "NAVigation System with Timing And Ranging." Each satellite circles the Earth every 12 hours in sidereal time along one of six orbital "planes" at an altitude of 20,200 km (about 12,500 miles). The satellites broadcast signals used by GPS receivers on the ground to measure positions. The satellites are arrayed such that at least four are "in view" everywhere on or near the Earth's surface at all times, with typically up to eight and potentially 12 "in view" at any given time.

Try This!
The U.S. Coast Guard's Navigation Center publishes status reports on the GPS satellite constellation. Its report of August 17, 2010, for example, listed 31 satellites, five to six in each of the six orbits planes (A-F), and one scheduled outage, on August 19, 2010. You can look up the current status of the constellation here.


15. Control Segment
The control segment of the Global Positioning System is a network of ground stations that monitors the shape and velocity of the satellites' orbits. The accuracy of GPS data depends on knowing the positions of the satellites at all times. The orbits of the satellites are sometimes disturbed by the interplay of the gravitational forces of the Earth and Moon.

Monitor Stations are very precise GPS receivers installed at known locations. They record discrepancies between known and calculated positions caused by slight variations in satellite orbits. Data describing the orbits are produced at the Master Control Station at Colorado Springs, uploaded to the satellites, and finally broadcast as part of the GPS positioning signal. GPS receivers use this satellite Navigation Message data to adjust the positions they measure.
If necessary, the Master Control Center can modify satellite orbits by commands transmitted via the control segment's ground antennas.
16. User Segment
The U.S. Federal Aviation Administration (FAA) estimated in 2006 that some 500,000 GPS receivers are in use for many applications, including surveying, transportation, precision farming, geophysics, and recreation, not to mention military navigation. This was before in-car GPS navigation gadgets emerged as one of the most popular consumer electronic gifts during the 2007 holiday season in North America.
Basic consumer-grade GPS receivers, like the rather old-fashioned one shown below, consist of a radio receiver and internal antenna, a digital clock, some sort of graphic and push-button user interface, a computer chip to perform calculations, memory to store waypoints, jacks to connect an external antenna or download data to a computer, and flashlight batteries for power. The radio receiver in the unit shown below includes 12 channels to receive signal from multiple satellites simultaneously.

NAVSTAR Block II satellites broadcast at two frequencies, 1575.42 MHz (L1) and 1227.6 MHz (L2). (For sake of comparison, FM radio stations broadcast in the band of 88 to 108 MHz.) Only L1 was intended for civilian use. Single-frequency receivers produce horizontal coordinates at an accuracy of about three to seven meters (or about 10 to 20 feet) at a cost of about $100. Some units allow users to improve accuracy by filtering out errors identified by nearby stationary receivers, a post-process called "differential correction." $300-500 single-frequency units that can also receive corrected L1 signals from the U.S. Federal Aviation Administration's Wide Area Augmentation System (WAAS) network of ground stations and satellites can perform differential correction in "real-time." Differentially-corrected coordinates produced by single-frequency receivers can be as accurate as one to three meters (about 3 to 10 feet).
The signal broadcast at the L2 frequency is encrypted for military use only. Clever GPS receiver makers soon figured out, however, how to make dual-frequency models that can measure slight differences in arrival times of the two signals (these are called "carrier phase differential" receivers). Such differences can be used to exploit the L2 frequency to improve accuracy without decoding the encrypted military signal. Survey-grade carrier-phase receivers able to perform real-time kinematic (RTK) differential correction can produce horizontal coordinates at sub-meter accuracy at a cost of $1000 to $2000. No wonder GPS has replaced electro-optical instruments for many land surveying tasks.
Meanwhile, a new generation of NAVSTAR satellites (the Block IIR-M series) will add a civilian signal at the L2 frequency that will enable substantially improved GPS positioning.
17. Satellite Ranging
GPS receivers calculate distances to satellites as a function of the amount of time it takes for satellites' signals to reach the ground. To make such a calculation, the receiver must be able to tell precisely when the signal was transmitted and when it was received. The satellites are equipped with extremely accurate atomic clocks, so the timing of transmissions is always known. Receivers contain cheaper clocks, which tend to be sources of measurement error. The signals broadcast by satellites, called "pseudo-random codes," are accompanied by the broadcast ephemeris data that describes the shapes of satellite orbits.

The GPS constellation is configured so that a minimum of four satellites is always "in view" everywhere on Earth. If only one satellite signal was available to a receiver, the set of possible positions would include the entire range sphere surrounding the satellite.

If two satellites are available, a receiver can tell that its position is somewhere along a circle formed by the intersection of two spherical ranges.

If distances from three satellites are known, the receiver's position must be one of two points at the intersection of three spherical ranges. GPS receivers are usually smart enough to choose the location nearest to the Earth's surface. At a minimum, three satellites are required for a two-dimensional (horizontal) fix. Four ranges are needed for a three-dimensional fix (horizontal and vertical).

Satellite ranging is similar in concept to the plane surveying method trilateration, by which horizontal positions are calculated as a function of distances from known locations. The GPS satellite constellation is in effect an orbiting control network.
Try This!
Trimble has a tutorial "designed to give you a good basic understanding of the principles behind GPS without loading you down with too much technical detail". Check it out at Trimble. Click "Why GPS?" to get started.

18. GPS Error Sources
A thought experiment (Wormley, 2004): Attach your GPS receiver to a tripod. Turn it on, and record its position every ten minutes for 24 hours. Next day, plot the 144 coordinates your receiver calculated. What do you suppose the plot would look like?
Do you imagine a cloud of points scattered around the actual location? That's a reasonable expectation. Now, imagine drawing a circle or ellipse that encompasses about 95 percent of the points. What would the radius of that circle or ellipse be? (In other words, what is your receiver's positioning error?)
The answer depends in part on your receiver. If you used a hundred-dollar receiver, the radius of the circle you drew might be as much as ten meters to capture 95 percent of the points. If you used a WAAS-enabled, single frequency receiver that cost a few hundred dollars, your error ellipse might shrink to one to three meters or so. But if you had spent a few thousand dollars on a dual frequency, survey-grade receiver, your error circle radius might be as small as a centimeter or less. In general, GPS users get what they pay for.
As the market for GPS positioning grows, receivers are becoming cheaper. Still, there are lots of mapping applications for which it's not practical to use a survey-grade unit. For example, if your assignment was to GPS 1,000 manholes for your municipality, you probably wouldn't want to set up and calibrate a survey-grade receiver 1,000 times. How, then, can you minimize errors associated with mapping-grade receivers? A sensible start is to understand the sources of GPS error.
In this section you will learn to:
- state the kinds and magnitude of error and uncertainty associated with uncorrected GPS positioning; and
- use a PDOP chart to determine the optimal times for GPS positioning at a given location and date.
Note: My primary source for the material in this section is Jan Van Sickle's text GPS for Land Surveyors, 2nd Ed. If you want a readable and much more detailed treatment of this material, I recommend Jan's book. See the bibliography at the end of this chapter for more information about this and other resources.
19. User Equivalent Range Errors
"UERE" is the umbrella term for all of the error sources below, which are presented in descending order of their contributions to the total error budget.
- Satellite clock: GPS receivers calculate their distances from satellites as a function of the difference in time between when a signal is transmitted by a satellite and when it is received on the ground. The atomic clocks on board NAVSTAR satellites are extremely accurate. They do tend to stray up to one millisecond of standard GPS time (which is calibrated to, but not identical to, Coordinated Universal Time). The monitoring stations that make up the GPS "Control Segment" calculate the amount of clock drift associated with each satellite. GPS receivers that are able to make use of the clock correction data that accompanies GPS signals can reduce clock error significantly.
- Upper atmosphere (ionosphere): Space is nearly a vacuum, but the atmosphere isn't. GPS signals are delayed and deflected as they pass through the ionosphere, the outermost layers of the atmosphere that extend from approximately 50 to 1,000 km above the Earth's surface. Signals transmitted by satellites close to the horizon take a longer route through the ionosphere than signals from satellites overhead, and are thus subject to greater interference. The ionosphere's density varies by latitude, by season, and by the time of day, in response to the Sun's ultraviolet radiation, solar storms and maximums, and the stratification of the ionosphere itself. The GPS Control Segment is able to model ionospheric biases, however. Monitoring stations transmit corrections to the NAVSTAR satellites, which then broadcast the corrections along with the GPS signal. Such corrections eliminate only about three-quarters of the bias, however, leaving the ionosphere the second largest contributor to the GPS error budget.
- Receiver clock: GPS receivers are equipped with quartz crystal clocks that are less stable than the atomic clocks used in NAVSTAR satellites. Receiver clock error can be eliminated, however, by comparing times of arrival of signals from two satellites (whose transmission times are known exactly).
- Satellite orbit: GPS receivers calculate coordinates relative to the known locations of satellites in space. Knowing where satellites are at any given moment involves knowing the shapes of their orbits as well as their velocities. The gravitational attractions of the Earth, Sun, and Moon all complicate the shapes of satellite orbits. The GPS Control Segment monitors satellite locations at all times, calculates orbit eccentricities, and compiles these deviations in documents called ephemerides. An ephemeris is compiled for each satellite and broadcast with the satellite signal. GPS receivers that are able to process ephemerides can compensate for some orbital errors.
- Lower atmosphere: (troposphere, tropopause, and stratosphere) The three lower layers of atmosphere encapsulate the Earth from the surface to an altitude of about 50 km. The lower atmosphere delays GPS signals, adding slightly to the calculated distances between satellites and receivers. Signals from satellites close to the horizon are delayed the most since they pass through more atmosphere than signals from satellites overhead.
- Multipath: Ideally, GPS signals travel from satellites through the atmosphere directly to GPS receivers. In reality, GPS receivers must discriminate between signals received directly from satellites and other signals that have been reflected from surrounding objects, such as buildings, trees, and even the ground. Some, but not all, reflected signals are identified automatically and rejected. Antennas are designed to minimize interference from signals reflected from below, but signals reflected from above are more difficult to eliminate. One technique for minimizing multipath errors is to track only those satellites that are at least 15° above the horizon, a threshold called the "mask angle."
Douglas Welsh (personal communication, Winter 2001), an Oil and Gas Inspector Supervisor with Pennsylvania's Department of Environmental Protection, wrote about the challenges associated with GPS positioning in our neck of the woods: "...in many parts of Pennsylvania the horizon is the limiting factor. In a city with tall buildings and the deep valleys of some parts of Pennsylvania, it is hard to find a time of day when the constellation will have four satellites in view for any amount of time. In the forests with tall hardwoods, multipath is so prevalent that I would doubt the accuracy of any spot unless a reading was taken multiple times." Van Sickle (2005) points out, however, that GPS modernization efforts and the GNSS may well ameliorate such gaps.
20. Dilution of Precision
The arrangement of satellites in the sky also affects the accuracy of GPS positioning. The ideal arrangement (of the minimum four satellites) is one satellite directly overhead, three others equally spaced near the horizon (above the mask angle). Imagine a vast umbrella that encompasses most of the sky, where the satellites form the tip and the ends of the umbrella spines.
GPS coordinates calculated when satellites are clustered close together in the sky suffer from dilution of precision (DOP), a factor that multiplies the uncertainty associated with User Equivalent Range Errors (UERE - errors associated with satellite and receiver clocks, the atmosphere, satellite orbits, and the environmental conditions that lead to multipath errors). The DOP associated with an ideal arrangement of the satellite constellation equals approximately 1, which does not magnify UERE. According to Van Sickle (2001), the lowest DOP encountered in practice is about 2, which doubles the uncertainty associated with UERE.
GPS receivers report several components of DOP, including Horizontal Dilution of Precision (HDOP) and Vertical Dilution of Precision (VDOP). The combination of these two components of the three-dimensional position is called PDOP - position dilution of precision. A key element of GPS mission planning is to identify the time of day when PDOP is minimized. Since satellite orbits are known, PDOP can be predicted for a given time and location. Various software products allow you to determine when conditions are best for GPS work.
MGIS student Jason Setzer (Winter 2006) offers the following illustrative anecdote:
I have had a chance to use GPS survey technology for gathering ground control data in my region and the biggest challenge is often the PDOP (position dilution of precision) issue. The problem in my mountainous area is the way the terrain really occludes the receiver from accessing enough satellite signals.
During one survey in Colorado Springs I encountered a pretty extreme example of this. Geographically, Colorado Springs is nestled right against the Rocky Mountain front ranges, with 14,000 foot Pike's Peak just west of the city. My GPS unit was easily able to 'see' five, six or even seven satellites while I was on the eastern half of the city. However, the further west I traveled, I began to see progressively less of the constellation, to the point where my receiver was only able to find one or two satellites. If a 180 degree horizon-to-horizon view of the sky is ideal, then in certain places I could see maybe 110 degrees.
There was no real work around, other than patience. I was able to adjust my survey points enough to maximize my view of the sky. From there it was just a matter of time... Each GPS bird has an orbit time of around twelve hours, so in a couple of instances I had to wait up to two hours at a particular location for enough of them to become visible. My GPS unit automatically calculates PDOP and displays the number of available satellites. So the PDOP value was never as low as I would have liked, but it did drop enough to finally be within acceptable limits. Next time I might send a vendor out for such a project!
Try This!
Trimble, a leading manufacturer of GPS receivers, offers on online GPS mission planning interface. This activity will introduce you to the capabilities of the interface and will prepare you to answer questions about GPS mission planning later.
The online tool that you will use in this exercise requires that Microsoft Silverlight be installed on your machine. Silverlight does not run under all Web browsers. If you do not have Silverlight installed for the browser you are using you be prompted to install it.
- Visit the Trimble website.
Hover your mouse cursor over Support & Training, and click on Support A-Z. - In the list of Support Products A-Z, find and click on the Planning Software link.
- On the Planning Software page that you land on, follow the Trimble GPS Data Resources link.
In the next step, you may be prompted to install Microsoft Silverlight.
If you are prompted to install Silverlight, go ahead and do so. There are Windows and Mac versions. The software will download, and then you will need to install it. Use the Run as Administrator option to do so. If the installation process comes back with a message that Silverlight is already installed, the implication is that you have more than one browser app installed on your machine and you just need to open the one that Silverlight is associated with. Chances are that it is Internet Explorer that you need to use.
- On the GPS Data Resources page, follow the GNSS Planning Tool link.
The GNSS Planning Online interface will open. You will land on the Settings page. - Go ahead and enter at least longitude and latitude information for a location you are interested in.
You can also use the Pick button to interactively select a location. After you pick a location from the map, click the Apply button. - Change or take note of the other setting in the Settings dialog window.
- Click the Settings window Apply button.
Your settings will be processed. Then you can click on any of the other buttons along the left side of the interface.
For example, the Satellite Library button gives you access to the satellites in the various GPS systems that exist. You can choose the satellites you want to use. Clicking on a satellite entry from one of the system lists will bring up its almanac information.
- Click the DOPs button. This allows you to see how the various sources of Dilution of Precision vary throughout the time period that was specified on the Settings page.
Can you determine the best and worst times of day for GPS work? - Spend some time investigating what the other buttons allow you to investigate.
Trimble's GNSS Planning Online tool is not a teaching tool; you will not find a Help button that links to explanations of the functionality. The planning tool is aimed at users already versed in the terminology and technology.

21. GPS Error Correction
A variety of factors, including the clocks in satellites and receivers, the atmosphere, satellite orbits, and reflective surfaces near the receiver, degrade the quality of GPS coordinates. The arrangement of satellites in the sky can make matters worse (a condition called dilution of precision). A variety of techniques have been developed to filter out positioning errors. Random errors can be partially overcome by simply averaging repeated fixes at the same location, although this is often not a very efficient solution. Systematic errors can be compensated for by modeling the phenomenon that causes the error and predicting the amount of offset. Some errors, like multipath errors caused when GPS signals are reflected from roads, buildings, and trees, vary in magnitude and direction from place to place. Other factors, including clocks, the atmosphere, and orbit eccentricities, tend to produce similar errors over large areas of the Earth's surface at the same time. Errors of this kind can be corrected using a collection of techniques called differential correction.
In this section you will learn to:
- explain the concept of differential correction and other methods used to improve the accuracy of GPS positioning; and
- perform differential correction using data and services of the U.S. National Geodetic Survey.
22. Differential Correction
Differential correction is a class of techniques for improving the accuracy of GPS positioning by comparing measurements taken by two or more receivers. Here's how it works:
The locations of two GPS receivers--one stationary, one mobile--are illustrated below in Figure 5.23.1. The stationary receiver (or "base station") continuously records its fixed position over a control point. The difference between the base station's actual location and its calculated location is a measure of the positioning error affecting that receiver at that location at each given moment. In this example, the base station is located about 25 kilometers from the mobile receiver (or "rover"). The operator of the mobile receiver moves from place to place. The operator might be recording addresses for an E-911 database, or trees damaged by gypsy moth infestations, or street lights maintained by a public works department.
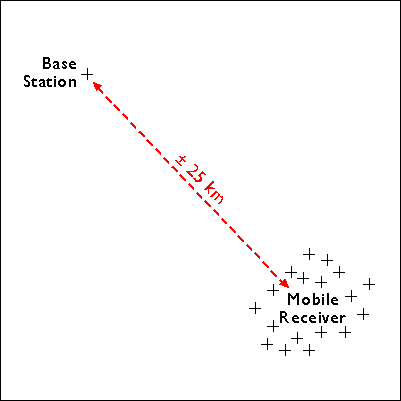
Figure 5.23.2, below, shows positions calculated at the same instant (3:01 pm) by the base station (left) and the mobile receiver (right).
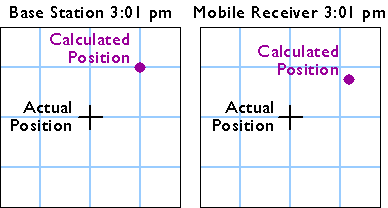
The base station calculates the correction needed to eliminate the error in the position calculated at that moment from GPS signals. The correction is later applied to the position calculated by the mobile receiver at the same instant. The corrected position is not perfectly accurate, because the kinds and magnitudes of errors affecting the two receivers are not identical, and because of the low frequency of the GPS timing code.
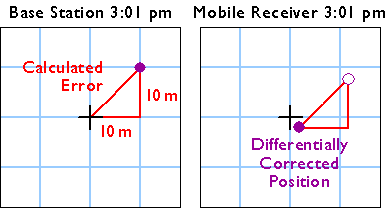

23. Real-Time Differential Correction
For differential correction to work, fixes recorded by the mobile receiver must be synchronized with fixes recorded by the base station (or stations). You can provide your own base station, or use correction signals produced from reference stations maintained by the U.S. Federal Aviation Administration, the U.S. Coast Guard, or other public agencies or private subscription services. Given the necessary equipment and available signals, synchronization can take place immediately ("real-time") or after the fact ("post-processing"). First let's consider real-time differential.
WAAS-enabled receivers are an inexpensive example of real-time differential correction. "WAAS" stands for Wide Area Augmentation System, a collection of about 25 base stations set up to improve GPS positioning at U.S. airport runways to the point that GPS can be used to help land airplanes (U.S. Federal Aviation Administration, 2007c). WAAS base stations transmit their measurements to a master station, where corrections are calculated and then uplinked to two geosynchronous satellites (19 are planned). The WAAS satellite then broadcasts differentially-corrected signals at the same frequency as GPS signals. WAAS signals compensate for positioning errors measured at WAAS base stations, as well as clock error corrections and regional estimates of upper-atmosphere errors (Yeazel, 2003). WAAS-enabled receivers devote one or two channels to WAAS signals, and are able to process the WAAS corrections. The WAAS network was designed to provide approximately 7-meter accuracy uniformly throughout its U.S. service area.
DGPS: The U.S. Coast Guard has developed a similar system, called the Differential Global Positioning Service. The DGPS network includes some 80 broadcast sites, each of which includes a survey-grade base station and a "radiobeacon" transmitter that broadcasts correction signals at 285-325 kHz (just below the AM radio band). DGPS-capable GPS receivers include a connection to a radio receiver that can tune in to one or more selected "beacons." Designed for navigation at sea near U.S. coasts, DGPS provides accuracies no worse than 10 meters. Stephanie Brown (personal communication, Fall 2003) reported that where she works in Georgia, "with a good satellite constellation overhead, [DGPS accuracy] is typically 4.5 to 8 feet."
Survey-grade real-time differential correction can be achieved using a technique called real-time kinematic (RTK) GPS. According to surveyor Laverne Hanley (personal communication, Fall 2000), "real-time kinematic requires a radio frequency link between a base station and the rover. I have achieved better than centimeter accuracy this way, although the instrumentation is touchy and requires great skill on the part of the operator. Several times I found that I had great GPS geometry, but had lost my link to the base station. The opposite has also happened, where I wanted to record positions and had a radio link back to the base station, but the GPS geometry was bad."
24. Post-Processed Differential Correction
Kinematic positioning can deliver accuracies of 1 part in 100,000 to 1 part in 750,000 with relatively brief observations of only one to two minutes each. For applications that require accuracies of 1 part in 1,000,000 or higher, including control surveys and measurements of movements of the Earth's tectonic plates, static positioning is required (Van Sickle, 2001). In static GPS positioning, two or more receivers measure their positions from fixed locations over periods of 30 minutes to two hours. The receivers may be positioned up to 300 km apart. Only dual frequency, carrier phase differential receivers capable of measuring the differences in time of arrival of the civilian GPS signal (L1) and the encrypted military signal (L2) are suitable for such high-accuracy static positioning.
CORS and OPUS: The U.S. National Geodetic Survey (NGS) maintains an Online Positioning User Service (OPUS) that enables surveyors to differentially-correct static GPS measurements acquired with a single dual frequency carrier phase differential receiver after they return from the field. Users upload measurements in a standard Receiver INdependent EXchange format (RINEX) to NGS computers, which perform differential corrections by referring to three selected base stations selected from a network of continuously operating reference stations. NGS oversees two CORS networks; one consisting of its 600 base stations of its own, another a cooperative of public and private agencies that agree to share their base station data and to maintain base stations to NGS specifications.
The map above shows the distribution of the combined national and cooperative CORS networks. Notice that station symbols are colored to denote the sampling rate at which base station data are stored. After 30 days, all stations are required to store base station data only in 30-second increments. This policy limits the utility of OPUS corrections to static positioning (although the accuracy of longer kinematic observations can also be improved). Mindful of the fact that the demand for static GPS is steadily declining, NGS' future plans include streaming CORS base station data for real-time use in kinematic positioning.
Try This!
This optional activity (contributed by Chris Piburn of CompassData Inc.) will guide you through the process of differentially-correcting static GPS measurements using the NGS' Online Positioning User Service (OPUS), which refers to the Continuously Operating Reference Station network (CORS).
The context is a CompassData project that involved a carrier phase differential GPS survey in a remote study area in Alaska. The objective was to survey a set of nine ground control points (GCPs) that would later be used to orthorectify a client's satellite imagery. So remote is this area that no NGS control point was available at the time the project was carried out. The alternative was to establish a base station for the project and to fix its position precisely with reference to CORS stations in operation elsewhere in Alaska.
The project team flew by helicopter to a hilltop located centrally within the study area. With some difficulty they hammered an 18 inch #5 rebar into the rocky soil to serve as a control monument. After setting up a GPS base station receiver over the rebar, they flew off to begin data collection with their rover receiver. Thanks to favorable weather, Chris and his team collected the nine required photo-identifiable GCPs on the first day. The centrally-located base station allowed the team to minimize distances between the base and the rover, which meant they could minimize the time required to fix each GCP. At the end of the day, the team had produced five hours of GPS data at the base station and nine fifteen-minute occupations at the GCPs
As you might expect, the raw GPS data were not sufficiently accurate to meet project requirements. (The various sources of random and systematic errors that contribute to the uncertainty of GPS data are considered elsewhere in this chapter.) In particular, the monument hammered into the hilltop was unsuitable for use as a control point because the uncertainty associated with its position was too great. The project team's first step in removing positioning errors was to post-process the data using baseline processing software, which adjusts computed baseline distances (between the base station and the nine GCPs) by comparing the phase of the GPS carrier wave as it arrived simultaneously at both the base station and the rover. The next step was to fix the position of the base station precisely in relation to CORS stations operating elsewhere in Alaska.
The following steps will guide you through the process of submitting the five hours of dual frequency base station data to the U.S. National Geodetic Survey's Online Positioning User Service (OPUS), and interpreting the results. (For information about OPUS, go here)
1. Download the GPS data file. The compressed RINEX format file is approximately 6 Mb in size and will take about 1 minute to download via high-speed DSL or cable, or about 15 minutes via 56 Kbps modem. If you can't download this file, contact me right away so we can help you resolve the problem.
- WILD282u.zip (5.8 Mb)
2. Examine the RINEX file.
- Extract the RINEX file "WILD282u.05O" from its ZIP archive.
- Open "WILD282u.05O" with Microsoft Notepad or WordPad. (WordPad does a better job of preserving columns of text in this case. Set the word wrap to off.) Or, use another text editor. (In any open text editor window, in the File > Open dialog, make sure "Files of type:" is set to "All files" so that the target file is listed.)
The RINEX Observation file contains all the information about the signals that CompassData's base station receiver tracked during the Alaska survey. Explaining all the contents of the file is well beyond the scope of this activity. For now, note the lines that disclose the antenna type, approximate position of the antenna, and antenna height. You'll report these parameters to OPUS in the next step.
3. Submit GPS data to OPUS.
- Point your browser to the OPUS home page, and enter the information needed in order to "Upload your data file."
- (OPUS step 1) Click the Browse button to call up a File Upload window. Navigate to and upload the RINEX file you downloaded earlier. To streamline your submission, choose the compressed archive "WILD282u.zip".
- (OPUS step 2) Select the antenna type. Refer to the line labeled "ANT # / TYPE" in the RINEX file you opened in your text editor. You should find the antenna type "TPSHIPER_PLUS". Choose this type from the pull-down list.
- (OPUS step 3) Enter the height of the antenna above the monument. Refer to the line labeled "ANTENNA: DELTA H/E/N" in the RINEX file you opened in your text editor. The first value on that line, "1.0854", is H, in meters. (See the OPUS website for more information about antenna height.)
- (OPUS step 4) Enter the email address to which you wish your results to be returned.
- (OPUS step 5) Options. OPUS allows users to specify a State Plane Coordinate system zone, to select or exclude particular CORS reference stations, to request standard or extended output, and to establish a user profile for use with future jobs. For this activity, no changes to the default settings are needed.
- (OPUS step 6) Click the "Upload to STATIC" button to submit the data for differential correction in relation to three CORS reference stations. Depending on how many requests are in NGS' queue, results may be returned in minutes or hours. When this activity was tested, the queue included only one request (see window below, which appears after requests successfully submitted) and results were returned in just a few minutes, but in the past, it has taken up to 10 minutes.
 Figure 5.25.2 Upload results report.Credit: Online Positioning User Service, U.S. National Geodetic Survey.
Figure 5.25.2 Upload results report.Credit: Online Positioning User Service, U.S. National Geodetic Survey.
When you receive your OPUS solution by return email, you will want to discover the magnitude of differential correction that OPUS calculated. To do this, you'll need to determine (a) the uncorrected position originally calculated by the base station, (b) the corrected position calculated by OPUS, and (c) the mark-to-mark distance between the original and corrected positions. In addition to the original RINEX file you downloaded earlier, you'll need the OPUS solution and two free software utilities provided by NGS. Links to these utilities are listed below.
4. Determine the position of the base station receiver prior to differential correction.
- Refer to the RINEX file "WILD282u.05O" you opened in your text editor. The ninth line of the RINEX file lists the position of the base station receiver in Earth-Centered Earth-Fixed X, Y, Z coordinates. This is a three-dimensional Cartesian coordinate system whose origin is the Earth's center of mass (like the NAD 83 datum).
-2389892.2740 -1608765.8567 5672855.7386 APPROX POSITION XYZ
NGS provides a conversion utility to transform these X, Y, Z values to more familiar latitude and longitude coordinates and ellipsoidal heights. - Go to NGS' XYZ to GEODETIC conversion.
- Enter the X, Y, Z coordinates found in the RINEX file. Your result should be:
- Latitude = 63°13'53.74280" N
- Longitude = 146°03'12.12710" W
- Height = 1349.2248 m
5. Determine the corrected position of the base station receiver. The OPUS solution you receive by email reports corrected coordinates in Earth-Centered Earth-Fixed X, Y, Z as geographic coordinates, and as UTM and State Plane coordinates. Look for the latitude and longitude coordinates and ellipsoidal height that are specified relative to the NAD 83 datum. They should be very close to:
- Latitude = 63°13'53.73892" N
- Longitude = 146°03'11.98942" W
- Height = 1348.756 m
6. Calculate the difference between the original and corrected base station positions. NGS provides another software utility to calculate the three-dimensional distance between two positions. Unlike the previous XYZ to GEODETIC converter, however, the "invers3d.exe" is a program you download to your computer.
- Download "invers3d.exe"
- Double-click on the file name to run the program, and choose the geodetic coordinates option.
- Paying close attention to the required formats, enter the uncorrected latitude, longitude, and ellipsoidal heights you calculated in step 4 above.
- Next, choose the geodetic coordinates option again and enter the corrected coordinates and height you calculated in step 5.
- Among the results, look for the calculated "mark-to-mark distance." This is the magnitude of the OPUS correction.

25. Summary
Positions are a fundamental element of geographic data. Sets of positions form features, as the letters on this page form words. Positions are produced by acts of measurement, which are susceptible to human, environmental, and instrument errors. Measurement errors cannot be eliminated, but systematic errors can be estimated and compensated for.
Land surveyors use specialized instruments to measure angles and distances, from which they calculate horizontal and vertical positions. The Global Positioning System (and, to a potentially greater extent, the emerging Global Navigation Satellite System) enables both surveyors and ordinary citizens to determine positions by measuring distances to three or more Earth-orbiting satellites. As you've read in this chapter (and may know from personal experience), GPS technology now rivals electro-optical positioning devices (i.e., "total stations" that combine optical angle measurement and electronic distance measurement instruments) in both cost and performance. This raises the question, "If survey-grade GPS receivers can produce point data with sub-centimeter accuracy, why are electro-optical positioning devices still so widely used?" In November 2005, I posed this question to two experts--Jan Van Sickle and Bill Toothill--whose work I had used as references while preparing this chapter. I also enjoyed a fruitful discussion with an experienced student named Sean Haile (Fall 2005). Here's what they had to say:
Jan Van Sickle, author of GPS for Land Surveyors and Basic GIS Coordinates, wrote:
In general it may be said that the cost of a good total station (EDM and theodolite combination) is similar to the cost of a good 'survey grade' GPS receiver. While a new GPS receiver may cost a bit more, there are certainly deals to be had for good used receivers. However, in many cases a RTK system that could offer production similar to an EDM requires two GPS receivers and there, obviously, the cost equation does not stand up. In such a case the EDM is less expensive.
Still, that is not the whole story. In some circumstances, such as large topographic surveys, the production of RTK GPS beats the EDM regardless of the cost differential of the equipment. Remember, you need line of sight with the EDM. Of course, if a topo survey gets too large, it is more cost effective to do the work with photogrammetry. And if it gets really large, it is most cost effective to use satellite imagery and remote sensing technology.
Now, lets talk about accuracy. It is important to keep in mind that GPS is not able to provide orthometric heights (elevations) without a geoid model. Geoid models are improving all the time, but are far from perfect. The EDM on the other hand has no such difficulty. With proper procedures it should be able to provide orthometric heights with very good relative accuracy over a local area. But, it is important to remember that relative accuracy over a local area with line of sight being necessary for good production (EDM) is applicable to some circumstances, but not others. As the area grows larger, as line of sight is at a premium, and a more absolute accuracy is required the advantage of GPS increases.
It must also be mentioned that the idea that GPS can provide cm level accuracy must always be discussed in the context of the question, 'relative to what control and on what datum?'
In relative terms, over a local area, using good procedures, it is certainly possible to say that an EDM can produce results superior to GPS in orthometric heights (levels) with some consistency. It is my opinion that this idea is the reason that it is rare for a surveyor to do detailed construction staking with GPS, i.e. curb and gutter, sewer, water, etc. On the other hand, it is common for surveyors to stake out property corners with GPS on a development site, and other features where the vertical aspect is not critical. It is not that GPS cannot provide very accurate heights, it is just that it takes more time and effort to do so with that technology when compared with EDM in this particular area (vertical component).
It is certainly true that GPS is not well suited for all surveying applications. However, there is no surveying technology that is well suited for all surveying applications. On the other hand, it is my opinion that one would be hard pressed to make the case that any surveying technology is obsolete. In other words, each system has strengths and weaknesses and that applies to GPS as well.
Bill Toothill, professor in the Department of GeoEnvironmental Sciences and Engineering at Wilkes University, wrote:
GPS is just as accurate at short range and more accurate at longer distances than electro-optical equipment. The cost of GPS is dropping and may not be much more than a high end electro-optical instrument. GPS is well suited for all surveying applications, even though for a small parcel (less than an acre) traditional instruments like a total station may prove faster. This depends on the availability of local reference sites (control) and the coordinate system reference requirements of the survey.
Most survey grade GPS units (dual frequency) can achieve centimeter level accuracies with fairly short occupation times. In the case of RTK this can be as little as five seconds with proper communication to a broadcasting 'base'. Sub-centimeter accuracies is another story. To achieve sub-centimeter, which most surveyors don't need, requires much longer occupation times which is not conducive for 'production' work in a business environment. Most sub-centimeter applications are used for research, most of which are in the geologic deformation category. I have been using dual frequency GPS for the last eight years in Yellowstone National Park studying the deformation of the Yellowstone Caldera. To achieve sub-centimeter results we need at least 4-6 hours of occupation time at each point along a transect.
Sean Haile, a U.S. Park Service employee at Zion National Park whose responsibilities include GIS and GPS work, takes issue with some of these statements, as well as with some of the chapter material. While a student in Fall 2005, Sean wrote:
A comparison of available products from [one manufacturer] shows that traditional technologies can achieve accuracy of 3mm. Under ideal conditions, the most advanced GPS equipment can only get down to 5mm accuracy, with real world results probably being closer to 10mm. It is true that GPS is often the faster and easier to use technology in the field when compared to electro-optical solutions, and with comparable accuracy levels has displaced traditional methods. If the surveyor needs to be accurate to the mm, however, electro-optical tools are more accurate than GPS.
There is no way, none, that you can buy a sub-centimeter unit anywhere for $1000-2000. Yes, the prices are falling, but it has only been recently (last three years) that you could even buy a single channel sub-meter accuracy GPS unit for under $10,000. The units you mention in the chapter for $1000-2000, they would be 'sell your next of kin' expensive during that same time period. I am not in the business of measuring tectonic plates, but I deal with survey and mapping grade differential correction GPS units daily, so I can speak from experience on that one.
And Bill's response that GPS is well suited for all survey applications? Well I sincerely beg to differ. GPS is poorly suited for surveying where there is limited view of the horizon. You could wait forever and never get the required number of SVs. Even with mission planning. Obstructions such as high canopy cover, tall buildings, big rock walls... all these things can result in high multi-path errors, which can ruin data from the best GPS units. None of these things affect EDM. Yes, you can overcome poor GPS collection conditions (to an extent) by offsetting your point from a location where signal is good, but when you do that, you are taking the exact measurements (distance, angle) that you would be doing with an EDM except with an instrument that is not suited to that application!
The Global Navigation Satellite System (GNSS) may eventually overcome some of the limitations of GPS positioning. Still, these experts seem to agree that both GPS and electro-optical surveying methods are here to stay.

26. Bibliography
Chapter 6: National Spatial Data Infrastructure I
1. Overview
Chapters 6 and 7 consider the origins and characteristics of the framework data themes that make up the United States' proposed National Spatial Data Infrastructure (NSDI). The seven themes include geodetic control, orthoimagery, elevation, transportation, hydrography, government units (administrative boundaries), and cadastral (property boundaries). Most framework data, like the printed topographic maps that preceded them, are derived directly or indirectly from aerial imagery. Chapter 6 introduces the field of photogrammetry, which is concerned with the production of geographic data from aerial imagery. The chapter begins by considering the nature and status of the U.S. NSDI in comparison with other national mapping programs. It considers the origins and characteristics of the geodetic control and orthoimagery themes. The remaining five themes are the subject of Chapter 7.
Objectives
Students who successfully complete Chapter 6 should be able to:
- explain how the distribution of authority for mapping and land title registration among various levels of government affects the availability of framework data;
- describe how topographic data are compiled from aerial imagery;
- explain the difference between a vertical aerial photograph and an orthoimage;
- list and describe characteristics and status of the USGS National Map; and
- discuss the relationship between the National Map and the NSDI framework.
"Try This!" Activities
Take a minute to complete any of the Try This activities that you encounter throughout the chapter. These are fun, thought provoking exercises to help you better understand the ideas presented in the chapter.

2. National Geographic Information Strategies
In 1998, Ian Masser published a comparative study of the national geographic information strategies of four developed countries: Britain (England and Wales), the Netherlands, Australia, and the United States. Masser built upon earlier work which found that countries with relatively low levels of digital data availability and GIS diffusion also tended to be countries where there had been a fragmentation of data sources in the absence of central or local government coordination” (p. ix). Comparing his four case studies in relation to the seven framework themes identified for the U.S. NSDI, Masser found considerable differences in data availability, pricing, and intellectual property protections. Differences in availability of core data, he found, are explained by the ways in which responsibilities for mapping and for land titles registration are distributed among national, state, and local governments in each country.
The following table summarizes those distributions of responsibilities.
| Government Level | Britain (England & Wales) | Netherlands | Australia | United States |
|---|---|---|---|---|
| Central government | Land titles registration, small- and large-scale mapping, statistical data | Land titles registration, small- and large-scale mapping, statistical data | Some small-scale mapping, statistical data | Small-scale mapping, statistical data |
| State/Territorial government | Not applicable | Not applicable | Land titles registration, small- and large-scale mapping | Some land titles registration and small- and large-scale mapping |
| Local government | None | large-scale mapping, population registers | Some large-scale mapping | Land titles registration, large-scale mapping |
Masser's analysis helps to explain what geospatial professionals in the U.S. have known all along -- that the coverage of framework data in the U.S. is incomplete or fragmented because thousands of local governments are responsible for large-scale mapping and land titles registration, and because these activities tend to be poorly coordinated. In contrast, core data coverage is more or less complete in Australia, the Netherlands, and Britain, where central and state governments have authority over large-scale mapping and land-titles registration.
Other differences among the four countries relate to fees charged by governments to use the geographic and statistical data they produce, as well as the copyright protections they assert over the data. U.S. federal government agencies, Masser notes, differ from their counterparts by charging no more than the cost of reproducing their data in forms suitable for delivery to customers. State and local government policies in the U.S. vary considerably, however. Longstanding debates persist in the U.S. about the viability and ethics of recouping costs associated with public data.
The U.S. also differs starkly from Britain and Australia in regards to copyright protection. Most data published by the U.S. Geological Survey or U.S. Census Bureau resides in the public domain and may be used without restriction. U.K. Ordnance Survey data, by contrast, is protected by Crown copyright, and is available for use by others for fees and under the terms of restrictive licensing agreements. One consequence of the federal government’s decision to release its geospatial data to the public domain, some have argued, was the early emergence of a vigorous geospatial industry in the U.S.
Try This!
To learn more about the Crown copyright policy of the Great Britain’s Ordnance Survey, search the Internet for “ordnance survey crown copyright.”
The USGS policy is explained here (or search on “acknowledging usgs as information source”)

3. Legacy Data: USGS Topographic Maps
Since the eighteenth century, the preparation of a detailed basic reference map has been recognized by the governments of most countries as fundamental for the delimitation of their territory, for underpinning their national defense and for management of their resources (Parry, 1987).
Specialists in geographic information recognize two broad functional classes of maps: reference maps and thematic maps. As you recall from Chapter 3, a thematic map is usually made with one particular purpose in mind. Often, the intent is to make a point about the spatial pattern of a single phenomenon. Reference maps, on the other hand, are designed to serve many different purposes. Like a reference book, such as a dictionary, encyclopedia, or gazetteer, reference maps help people look up facts. Common uses of reference maps include locating place names and features, estimating distances, directions, and areas, and determining preferred routes from starting points to a destination. Reference maps are also used as base maps upon which additional geographic data can be compiled. Because reference maps serve various uses, they typically include a greater number and variety of symbols and names than thematic maps. The portion of the United States Geological Survey (USGS) topographic map shown below is a good example.

The term topography derives from the Greek topographein, "to describe a place." Topographic maps show, and name, many of the visible characteristics of the landscape, as well as political and administrative boundaries. Topographic map series provide base maps of uniform scale, content, and accuracy (more or less) for entire territories. Many national governments include agencies responsible for developing and maintaining topographic map series for a variety of uses, from natural resource management to national defense. Affluent countries, countries with especially valuable natural resources, and countries with large or unusually active militaries tend to be mapped more completely than others.
The systematic mapping of the entire U.S. began in 1879 when the U.S. Geological Survey (USGS) was established. Over the next century, USGS and its partners created topographic map series at several scales, including 1:250,000, 1:100,000, 1:63,360, and 1:24,000. The diagram below illustrates the relative extents of the different map series. Since much of today’s digital map data was digitized from these topographic maps, one of the challenges of creating continuous digital coverage of the entire U.S. is to seam together all of these separate map sheets.

Map sheets in the 1:24,000-scale series are known as quadrangles or simply quads. A quadrangle is a four-sided polygon. Although each 1:24,000 quad covers 7.5 minutes longitude by 7.5 minutes latitude, their shapes and area coverage vary. The area covered by the 7.5-minute maps varies from 49 to 71 square miles (126 to 183 square kilometers) because the length of a degree of longitude varies with latitude.

Through the 1940s, topographers in the field compiled by hand the data depicted on topographic maps. Anson (2002) recalls being outfitted with a 14 inch x 14-inch tracing table and tripod, plus an alidade [a 12 inch telescope mounted on a brass ruler], a 13 foot folding stadia rod, a machete, and a canteen... (p. 1). Teams of topographers sketched streams, shorelines, and other water features; roads, structures, and other features of the built environment; elevation contours, and many other features. To ensure geometric accuracy, their sketches were based upon geodetic control provided by land surveyors, as well as positions and spot elevations they surveyed themselves using alidades and rods. Depending on the terrain, a single 7.5-minute quad sheet might take weeks or months to compile. In the 1950s, however, photogrammetric methods involving stereoplotters that permitted topographers to make accurate stereoscopic measurements directly from overlapping pairs of aerial photographs provided a viable and more efficient alternative to field mapping. We’ll consider photogrammetry in greater detail later on in this chapter.
By 1992, the series of over 53,000 separate quadrangle maps covering the lower 48 states, Hawaii, and U.S. territories at 1:24,000 scale was completed, at an estimated total cost of $2 billion. However, by the end of the century, the average age of 7.5-minute quadrangles was over 20 years, and federal budget appropriations limited revisions to only 1,500 quads a year (Moore, 2000). As landscape change has exceeded revisions in many areas of the U.S., the USGS topographic map series has become legacy data outdated in terms of format as well as content.
Try This!
Search the Internet on "USGS topographic maps" to investigate the history and characteristics of USGS topographic maps in greater depth. View preview images, look up publication and revision dates, and order topographic maps at "USGS Store."

4. Accuracy Standards
Errors and uncertainty are inherent in geographic data. Despite the best efforts of the USGS Mapping Division and its contractors, topographic maps include features that are out of place, features that are named or symbolized incorrectly, and features that are out of date.
As discussed in Chapter 2, the locational accuracy of spatial features encoded in USGS topographic maps and data are guaranteed to conform to National Map Accuracy Standards. The standard for topographic maps state that horizontal positions of 90 percent of the well-defined points tested will occur within 0.02 inches (map distance) of their actual positions. Similarly, the vertical positions of 90 percent of well-defined points tested are to be true to within one-half of the contour interval. Both standards, remember, are scale-dependent.
Objective standards do not exist for the accuracy of attributes associated with geographic features. Attribute errors certainly do occur, however. A chronicler of the national mapping program (Thompson, 1988, p. 106) recalls a worried user who complained to USGS that "My faith in map accuracy received a jolt when I noted that on the map the borough water reservoir is shown as a sewage treatment plant."
The passage of time is perhaps the most troublesome source of errors on topographic maps. As mentioned in the previous page, the average age of USGS topographic maps is over 20 years. Geographic data quickly lose value (except for historical analyses) unless they are continually revised. The sequence of map fragments below show how frequently revisions were required between 1949 and 1973 for the quad that covers Key Largo, Florida. Revisions are based primarily on geographic data produced by aerial photography.

Try This!
Investigate standards for data quality and other characteristics of U.S. national map data here or by searching the Internet for "usgs national map accuracy standards".

5. Scanned Topographic Maps
Many digital data products have been derived from the USGS topographic map series. The simplest of such products are Digital Raster Graphics (DRGs). DRGs are scanned raster images of USGS 1:24,000 topographic maps. DRGs are useful as backdrops over which other digital data may be superimposed. For example, the accuracy of a vector file containing lines that represent lakes, rivers, and streams could be checked for completeness and accuracy by plotting it over a DRG.

DRGs are created by scanning paper maps at 250 pixels per inch resolution. Since at 1:24,000 1 inch on the map represents 2,000 feet on the ground, each DRG pixel corresponds to an area about 8 feet (2.4 meters) on a side. Each pixel is associated with a single attribute: a number from 0 to 12. The numbers stand for the 13 standard DRG colors.

Like the paper maps from which they are scanned, DRGs comply with National Map Accuracy Standards. A subset of the more than 50,000 DRGs that cover the lower 48 states have been sampled and tested for completeness and positional accuracy.
DRGs conform to the Universal Transverse Mercator projection used in the local UTM zone. The scanned images are transformed to the UTM projection by matching the positions of 16 control points. Like topographic quadrangle maps, all DRGs within one UTM zone can be fit together to form a mosaic after the map "collars" are removed.
Check out USA Topo Maps, a web map that provides a seamless digital compilation of USGS topographic maps for the entire United States. This is a multi-scale web map hosted in ArcGIS Online. As you zoom in, you'll view different scales of digitized topographic maps. The largest-scale images are built from USGS DRGs.
Try This!
Explore a DRG with Global Mapper
You can use a free software application called Global Mapper to investigate the characteristics of a USGS Digital Raster Graphic. Originally developed by the staff of the USGS Mapping Division at Rolla, Missouri as a data viewer for USGS data, Global Mapper has since been commercialized but is available in a free trial version. The instructions below will guide you through the process of installing the software and opening the DRG data.
Note: Global Mapper is a Windows application and will not run under the Macintosh operating system.
Global Mapper Installation Instructions
Skip this step if you already downloaded and installed Global Mapper.
- Navigate to globalmapper.com or search the Internet for “Global Mapper”
- Download the trial version of the software.
- Double-click on the setup file you downloaded to install the program.
- Launch Global Mapper.
Downloading and exploring DRG data in Global Mapper
- First, create a directory called "USGS Data" on your hard disk, where you can file your materials.
- Download the DRG.zip data archive. The ZIP archive is 2.7 Mb in size and will take approximately 35 seconds to download via high-speed DSL or cable, or about 9 minutes and 35 seconds via 56 Kbps modem.
- Now, decompress the archive into a directory on your hard disk.
- Open the ZIP archive you downloaded.
- Extract all files in the ZIP archive into a known subdirectory.
- Open your DRG in Global Mapper.
- Choose File > Open Data File(s)..., then navigate to the subdirectory into which you extracted the DRG files.
- Open the file 'bushkill_pa.tif'
- Notice that as you glide the magnifying glass cursor over the DRG, the UTM (NAD 27) and geographic coordinates of the cursor's position change in the lower right-hand corner of the window. This tells you that the DRG is in fact georeferenced.
- Experiment with Global Mapper’s tools. Use the Zoom and Pan tools to magnify and scroll across the DRG. The Full View button (the one with the house icon) refreshes the initial full view of the data set.
- The Measure tool (ruler icon) allows you to not only measure distance as the crow flies but also to see the area enclosed by a series of line segments drawn by repeated mouse clicks. Note again the location information that is given to you near the bottom of the application window.
Certain tools, e.g., the 3D Path Profile/Line of Sight tool, are not functional in the free (unregistered) version of Global Mapper.
- To view an excerpt from the DRG metadata, navigate to Tools > Control Center, then click the Metadata button.

6. Federal Geographic Data Committee
Even before the USGS completed its nationwide 7.5-minute quadrangle series, the U.S. federal government had begun to rethink and reorganize its national mapping program. In 1990, the U.S. Office of Management and Budget issued Circular A-16, which established the Federal Geographic Data Committee (FGDC) as the interagency coordinating body responsible for facilitating cooperation among federal agencies whose missions include producing and using geospatial data. FGDC is chaired by the Department of Interior, and is administered by USGS.
In 1994, President Bill Clinton’s Executive Order 12906 charged the FGDC with coordinating the efforts of government agencies and private sector firms leading to a National Spatial Data Infrastructure (NSDI). The Order defined NSDI as "the technology, policies, standards and human resources necessary to acquire, process, store, distribute, and improve utilization of geospatial data" (White House, 1994). It called upon FGDC to establish a National Geospatial Data Clearinghouse, ordered federal agencies to make their geospatial data products available to the public through the Clearinghouse, and required them to document data in a standard format that facilitates Internet search. Agencies were required to produce and distribute data in compliance with standards established by FGDC. (The Departments of Defense and Energy were exempt from the order, as was the Central Intelligence Agency.)
Finally, the Order charged FGDC with preparing an implementation plan for a National Digital Geospatial Data Framework, the "data backbone of the NSDI" (FGDC, 1997, p. v). The seven core data themes that comprise the NSDI Framework are listed below, along with the government agencies that have lead responsibility for creating and maintaining each theme. Later on in this chapter, and in the one that follows, we’ll investigate the framework themes one by one.
| Geodetic Control | Department of Commerce, National Oceanographic and Atmospheric Administration, National Geodetic Survey |
|---|---|
| Orthoimagery | Department of Interior, U.S. Geological Survey |
| Elevation | Department of Interior, U.S. Geological Survey |
| Transportation | Department of Transportation |
| Hydrography | Department of Interior, U.S. Geological Survey |
| Administrative units (boundaries) | Department of Commerce, U.S. Census Bureau |
| Cadastral | Department of Interior, Bureau of Land Management |
Seven data themes that comprise the NSDI Framework and the government agencies responsible for each.
7. USGS National Map
Executive Order 12906 decreed that a designee of the Secretary of the Department of Interior would chair the Federal Geographic Data Committee. The USGS, an agency of the Department of Interior, has lead responsibility for three of the seven NSDI framework themes--orthoimagery, elevation, and hydrography, and secondary responsibility for several others. In 2001, USGS announced its vision of a National Map that "aligns with the goals of, and is one of several USGS activities that contribute to, the National Spatial Data Infrastructure" (USGS, 2001, p. 31). A 2002 report of the National Research Council identified the National Map as the most important initiative of USGS’ Geography Discipline at the USGS (NRC, 2002). Recognizing its unifying role across its science disciplines, USGS moved management responsibility for the National Map from Geography to the USGS Geospatial Information Office in 2004. (One reason that the term "geospatial" is used at USGS and elsewhere is to avoid association of GIS with a particular discipline, i.e., Geography.)
In 2001, USGS envisioned the National Map as the Nation’s topographic map for the 21st Century (USGS, 2001, p.1). Improvements over the original topographic map series were to include:
| Currentness | Content will be updated on the basis of changes in the landscape instead of the cyclical inspection and revisions cycles now in use [for printed topographic map series]. The ultimate goal is that new content be incorporated with seven days of a change in the landscape. |
|---|---|
| Seamlessness | Features will be represented in their entirety and not interrupted by arbitrary edges, such as 7.5-minute map boundaries. |
| Consistent classification | Types of features, such as "road" and "lake/pond," will be identified in the same way throughout the Nation. |
| Variable resolution | Data resolution, or pixel size, may vary among imagery of urban, rural, and wilderness areas. The resolution of elevation data may be finer for flood plain, coastal, and other areas of low relief than for areas of high relief. |
| Completeness | Data content will include all mappable features (as defined by the applicable content standards for each data theme and source). |
| Consistency and integration | Content will be delineated geographically (that is, in its true ground position within the applicable accuracy limit) to ensure logical consistency between related features. For example, ... streams and rivers [should] consistently flow downhill... |
| Variable positional accuracy | The minimum positional accuracy will be that of the current primary topographic map series for an area. Actual positional accuracy will be reported in conformance with the Federal Geographic Data Committee’s Geospatial Positioning Accuracy Standard. |
| Spatial reference systems | Tools will be provided to integrate data that are mapping using different datums and referenced to different coordinates systems, and to reproject data to meet user requirements. |
| Standardized content | ...will conform to appropriate Federal Geographic Data Committee, other national, and/or international standards. |
| Metadata | At a minimum, metadata will meet Federal Geographic Data Committee standards to document ... [data] lineage, positional and attribute accuracy, completeness, and consistency. |
To this day, USGS’ ambitious vision is still being realized. The basic elements have been in place for a while — national data themes, data access and dissemination technologies such as Data.gov and the National Map viewer. But, ongoing is the cooperation by many federal, state and local government agencies, in order to keep making available new data as it is collected and compiled. A Center of Excellence for Geospatial Information Science (CEGIS) has been established under the USGS Geospatial Information Office to undertake the basic GIScience research needed to devise and implement advanced tools that will make the National Map more valuable to end users.
The data themes included in the National Map are shown in the following table, in comparison to the NSDI framework themes outlined earlier in this chapter. As you see, the National Map themes align with five of the seven framework themes, but do not include geodetic control and cadastral data. Also, the National Map adds land cover and geographic names, which are not included among the NSDI framework themes. Given USGS’ leadership role in FGDC, why do the National Map themes deviate from the NSDI framework? According to the Committee on Research Priorities for the USGS Center of Excellence for Geospatial Science, “these themes were selected because USGS is authorized to provide them if no other sources are available, and [because] they typically comprise the information portrayed on USGS topographic maps (NRC, 2007, p. 31).
|
Type |
National Map Themes | NSDI Framework Themes |
|---|---|---|
| Geodetic Control | No | Yes |
| Orthoimagery | Yes | Yes |
| Land Cover | Yes | No |
| Elevation | Yes | Yes |
| Transportation | Yes | Yes |
| Hydrography | Yes | Yes |
| Boundaries | Yes | Yes |
| Structures | Yes | No |
| Cadastral | No | Yes |
| Geographic Names | Yes | No |
The following sections of this chapter and the one that follows will describe the derivation, characteristics, and status of the seven NSDI themes in relation to the National Map. Chapter 8, Remotely Sensed Image Data, will include a description of the National Land Cover Data program that provides the land cover theme of the National Map.
8. Theme: Geodetic Control
In the U.S., the National Geodetic Survey (NGS) maintains a national geodetic control network called the National Spatial Reference System (NSRS). The NSRS includes approximately 300,000 horizontal and 600,000 vertical control points (Doyle, 1994). High-accuracy control networks are needed for mapping projects that span large areas; to design and maintain interstate transportation corridors including highways, pipelines, and transmission lines; and to monitor tectonic movements of the Earth's crust and sea level changes, among other applications (FGDC, 1998a).
Some control points are more accurate than others, depending on the methods surveyors used to establish them. The Chapter 5 page titled "Survey Control" outlines the accuracy classification adopted in 1988 for control points in the NSRS. As geodetic-grade GPS technology has become affordable for surveyors, expectations for control network accuracy have increased. In 1998, the FGDC's Federal Geodetic Control Subcommittee published a set of Geospatial Positioning Accuracy Standards. One of these is the Standards for Geodetic Networks (FGDC, 1998a). The table below presents the latest accuracy classification for horizontal coordinates and heights (ellipsoidal and orthometric). For example, the theoretically infinitesimal location of a horizontal control point classified as "1-Millimeter" must have a 95% likelihood of falling within a 1 mm "radius of uncertainty" (FGDC, 1998b, 1-5).
| Accuracy Classification | Radius of Uncertainty (95% confidence) |
|---|---|
| 1-Millimeter | 0.001 meters |
| 2-Millimeter | 0.002 meters |
| 5-Millimeter | 0.005 meters |
| 1-Centimeter | 0.010 meters |
| 2-Centimeter | 0.020 meters |
| 5-Centimeter | 0.050 meters |
| 1-Decimeter | 0.100 meters |
| 2-Decimeter | 0.200 meters |
| 5-Decimeter | 0.500 meters |
| 1-Meter | 1.000 meters |
| 2-Meter | 2.000 meters |
| 5-Meter | 5.000 meters |
| 10-Meter | 10.000 meters |
If in Chapter 2 you retrieved a NGS datasheet for a control point, you probably found that the accuracy of your point was reported in terms of the 1988 classification. If yours was a "first order" (C) control point, its accuracy classification is 1 centimeter. NGS does plan to upgrade the NSRS, however. Its 10-year strategic plan states that "the geodetic latitude, longitude and height of points used in defining NSRS should have an absolute accuracy of 1 millimeter at any time" (NGS, 2007, 8).
Think About It
Why does the 1998 standard refer to absolute accuracies while the 1988 standard (outlined in Chapter 5) is defined in terms of maximum error relative to distance between two survey points? What changed between 1988 and 1998 in regard to how control points are established?

9. Theme: Orthoimagery
The Federal Geographic Data Committee (FGDC, 1997, p. 18) defines orthoimage as "a georeferenced image prepared from an aerial photograph or other remotely sensed data ... [that] has the same metric properties as a map and has a uniform scale." Unlike orthoimages, the scale of ordinary aerial images varies across the image, due to the changing elevation of the terrain surface (among other things). The process of creating an orthoimage from an ordinary aerial image is called orthorectification. Photogrammetrists are the professionals who specialize in creating orthorectified aerial imagery, and in compiling geometrically-accurate vector data from aerial images. So, to appreciate the requirements of the orthoimagery theme of the NSDI framework, we first need to investigate the field of photogrammetry.
10. Photogrammetry
Photogrammetry is a profession concerned with producing precise measurements of objects from photographs and photoimagery. One of the objects measured most often by photogrammetrists is the surface of the Earth. Since the mid-20th century, aerial images have been the primary source of data used by USGS and similar agencies to create and revise topographic maps. Before then, topographic maps were compiled in the field using magnetic compasses, tapes, plane tables (a drawing board mounted on a tripod, equipped with an leveling telescope like a transit), and even barometers to estimate elevation from changes in air pressure. Although field surveys continue to be important for establishing horizontal and vertical control, photogrammetry has greatly improved the efficiency and quality of topographic mapping.
A straight line between the center of a lens and the center of a visible scene is called an optical axis. A vertical aerial photograph is a picture of the Earth's surface taken from above with a camera oriented such that its optical axis is vertical. In other words, when a vertical aerial photograph is exposed to the light reflected from the Earth's surface, the sheet of photographic film (or a digital imaging surface) is parallel to the ground. In contrast, an image you might create by snapping a picture of the ground below while traveling in an airplane is called an oblique aerial photograph, because the camera's optical axis forms an oblique angle with the ground.

The nominal scale of a vertical air photo is equivalent to f / H, where f is the focal length of the camera (the distance between the camera lens and the film -- usually six inches), and H is the flying height of the aircraft above the ground. It is possible to produce a vertical air photo such that scale is consistent throughout the image. This is only possible, however, if the terrain in the scene is absolutely flat. In rare cases where that condition is met, topographic maps can be compiled directly from vertical aerial photographs. Most often, however, air photos of variable terrain need to be transformed, or rectified, before they can be used as a source for mapping.
Government agencies at all levels need up-to-date aerial imagery. Early efforts to sponsor complete and recurring coverage of the U.S. included the National Aerial Photography Program, which replaced an earlier National High Altitude Photography program in 1987. NAPP was a consortium of federal government agencies that aimed to jointly sponsor vertical aerial photography of the entire lower 48 states every seven years or so at an altitude of 20,000 feet, suitable for producing topographic maps at scales as large as 1:5,000. More recently, NAPP has been eclipsed by another consortium called the National Agricultural Imagery Program. According to student Anne O'Connor (personal communication, Spring 2004), who represented the Census Bureau in the consortium:
A large portion of the country is flown yearly in the NAIP program due to USDA compliance needs. One problem is that it is leaf on, therefore in areas of dense foliage, some features are obscured. NAIP imagery is produced using partnership funds from USDA, USGS, FEMA, BLM, USFS and individual states. Other partnerships (between agencies or an agency and state) are also developed depending upon agency and local needs.
Aerial photography missions involve capturing sequences of overlapping images along many parallel flight paths. In the portion of the air photo mosaic shown below, note that the photographs overlap one another end to end and side to side. This overlap is necessary for stereoscopic viewing, which is the key to rectifying photographs of variable terrain. It takes about 10 overlapping aerial photographs taken along two adjacent north-south flightpaths to provide stereo coverage for a 7.5-minute quadrangle.

Try This!
Use the USGS' EarthExplorer (http://earthexplorer.usgs.gov/) to identify vertical aerial photographs that show the "address/place" in which you live. How old are the photos? (EarthExplorer is part of a USGS data distribution system.)
Note: The basemap imagery that you see on the EarthExplorer map is not the same as the NAPP photos the system allows you to identify and order. By the end of this chapter, you should know the difference!

11. Perspective and Planimetry
To understand why topographic maps can't be traced directly off of most vertical aerial photographs, you first need to appreciate the difference between perspective and planimetry. In a perspective view, all light rays reflected from the Earth's surface pass through a single point at the center of the camera lens. A planimetric (plan) view, by contrast, looks as though every position on the ground is being viewed from directly above. Scale varies in perspective views. In plan views, scale is everywhere consistent (if we overlook variations in small-scale maps due to map projections). Topographic maps are said to be planimetrically correct. So are orthoimages. Vertical aerial photographs are not, unless they happen to be taken over flat terrain.
As discussed above, the scale of an aerial photograph is partly a function of flying height. Thus, variations in elevation cause variations in scale on aerial photographs. Specifically, the higher the elevation of an object, the farther the object will be displaced from its actual position away from the principal point of the photograph (the point on the ground surface that is directly below the camera lens). Conversely, the lower the elevation of an object, the more it will be displaced toward the principal point. This effect, called relief displacement, is illustrated below in Figure 6.12.1. Note that the effect increases with distance from the principal point.

At the top of the diagram above, light rays reflected from the surface converge upon a single point at the center of the camera lens. The smaller trapezoid below the lens represents a sheet of photographic film. (The film actually is located behind the lens, but since the geometry of the incident light is symmetrical, we can minimize the height of the diagram by showing a mirror image of the film below the lens.) Notice the four triangular fiducial marks along the edges of the film. The marks point to the principal point of the photograph, which corresponds with the location on the ground directly below the camera lens at the moment of exposure. Scale distortion is zero at the principal point. Other features shown in the photo may be displaced toward or away from the principal point, depending on the elevation of the terrain surface. The larger trapezoid represents the average elevation of the terrain surface within a scene. On the left side of the diagram, a point on the land surface at a higher than average elevation is displaced outwards, away from the principal point and its actual location. On the right side, another location at less than average elevation is displaced towards the principal point. As terrain elevation increases, flying height decreases and photo scale increases. As terrain elevation decreases, flying height increases and photo scale decreases.
Compare the map and photograph below in Figure 6.12.2. Both show the same gas pipeline, which passes through hilly terrain. Note the deformation of the pipeline route in the photo relative to the shape of the route on the topographic map. The deformation in the photo is caused by relief displacement. The photo would not serve well on its own as a source for topographic mapping.

Still confused? Think of it this way: where the terrain elevation is high, the ground is closer to the aerial camera, and the photo scale is a little larger than where the terrain elevation is lower. Although the altitude of the camera is constant, the effect of the undulating terrain is to zoom in and out. The effect of continuously-varying scale is to distort the geometry of the aerial photo. This effect is called relief displacement.
Distorted perspective views can be transformed into plan views through a process called rectification. In Summer 2001, student Joel Hamilton recounted one very awkward way to rectify aerial photographs:
"Back in the mid 80's I saw a very large map being created from a multitude of aerial photos being fitted together. A problem that arose was that roads did not connect from one photo to the next at the outer edges of the map. No computers were used to create this map. So using a little water to wet the photos on the outside of the map, the photos were stretched to correct for the distortions. Starting from the center of the map the mosaic map was created. A very messy process."
Nowadays, digital aerial photographs can be rectified in an analogous (but much less messy) way, using specialized photogrammetric software that shifts image pixels toward or away from the principal point of each photo in proportion to two variables: the elevation of the point of the Earth's surface at the location that corresponds to each pixel, and each pixel's distance from the principal point of the photo.
Another even simpler way to rectify perspective images is to view pairs of images stereoscopically.
12. Stereoscopy
If you have normal or corrected vision in both eyes, your view of the world is stereoscopic. Viewing your environment simultaneously from two slightly different perspectives enables you to estimate very accurately which objects in your visual field are nearer, and which are farther away. You know this ability as depth perception.
When you fix your gaze upon an object, the intersection of your two optical axes at the object form what is called a parallactic angle. On average, people can detect changes as small as 3 seconds in the parallactic angle, an angular resolution that compares well to transits and theodolites. The keenness of human depth perception is what makes photogrammetric measurements possible.
Your perception of a three-dimensional environment is produced from two separate two-dimensional images. The images produced by your eyes are analogous to two aerial images taken one after another along a flight path. Objects that appear in the area of overlap between two aerial images are seen from two different perspectives. A pair of overlapping vertical aerial images is called a stereopair. When a stereopair is viewed such that each eye sees only one image, it is possible to envision a three-dimensional image of the area of overlap.
On the following page, you'll find a couple of examples of how stereoscopy is used to create planimetrically-correct views of the Earth's surface. If you have anaglyph stereo (red/blue) glasses, you'll be able to see stereo yourself. First, let's practice viewing anaglyph stereo images.
Try This!
One way to see in stereo is with an instrument called a stereoscope (see examples on the Interpreting Imagery page at James Madison University's Spatial Information Clearinghouse). Another way that works on computer screens and doesn't require expensive equipment is called anaglyph stereo (anaglyph comes from a Greek word that means, "to carve in relief"). The anaglyph method involves special glasses in which the left and right eyes are covered by blue and red filters.
The anaglyph image shown below consists of a superimposed stereopair in which the left image is shown in red and the right image is shown in green and blue. The filters in the glasses ensure each eye sees only one image. Can you make out the three-dimensional image of the U-shaped valley formed by glaciers in the French Alps?

How about this one: a panorama of the surface of Mars imaged during the Pathfinder mission, July 1997?

To find other stereo images on the World Wide Web, search on "anaglyph."

13. Rectification by Stereoscopy
Aerial images need to be transformed from perspective views into plan views before they can be used to trace the features that appear on topographic maps, or to digitize vector features in digital data sets. One way to accomplish the transformation is through stereoscopic viewing.
Below in Figure 6.14.1 are portions of a vertical aerial photograph and a topographic map that show the same area, a synclinal ridge called "Little Mountain" on the Susquehanna River in central Pennsylvania. A linear clearing, cut for a power line, appears on both (highlighted in yellow on the map). The clearing appears crooked on the photograph due to relief displacement. Yet we know that an aerial image like this one was used to compile the topographic map. The air photo had to have been rectified to be used as a source for topographic mapping.

Below in Figure 6.14.2 are portions of two aerial photographs showing Little Mountain. The two photos were taken from successive flight paths. The two perspectives can be used to create a stereopair.

Next, the stereopair is superimposed in an anaglyph image. Using your red/blue glasses, you should be able to see a three-dimensional image of Little Mountain in which the power line appears straight, as it would if you were able to see it in person. Notice that the height of Little Mountain is exaggerated due to the fact that the distance between the principal points of the two photos is not exactly proportional to the distance between your eyes.

Let's try that again. We need to make sure that you can visualize how stereoscopic viewing transforms overlapping aerial photographs from perspective views into planimetric views. The aerial photograph and topographic map portions below show the same features, a power line clearing crossing the Sinnemahoning Creek in Central Pennsylvania. The power line appears to bend as it descends to the creek because of relief displacement.

Two aerial photographs of the same area taken from different perspectives constitute a stereo pair.

By viewing the two photographs stereoscopically, we can transform them from two-dimensional perspective views to a single three-dimensional view in which the geometric distortions caused by relief displacement have been removed.

Photogrammetrists use instruments called stereoplotters to trace, or compile, the data shown on topographic maps from stereoscopic images like the ones you've seen here. The operator pictured below is viewing a stereoscopic model similar to the one you see when you view the anaglyph stereo images with red/blue glasses. A stereopair is superimposed on the right-hand screen of the operator's workstation. The left-hand screen shows dialog boxes and command windows through which she controls the stereoplotter software. Instead of red/blue glasses, the operator is wearing glasses with polarized lens filters that allow her to visualize a three-dimensional image of the terrain. She handles a 3-D mouse that allows her to place a cursor on the terrain image within inches of its actual horizontal and vertical position.

14. Orthorectification
An orthoimage (or orthophoto) is a single aerial image in which distortions caused by relief displacement have been removed. The scale of an orthoimage is uniform. Like a planimetrically correct map, orthoimages depict scenes as though every point were viewed simultaneously from directly above. In other words, as if every optical axis were orthogonal to the ground surface. Notice how the power line clearing has been straightened in the orthophoto on the right, below in Figure 6.15.1.

Relief displacement is caused by differences in elevation. If the elevation of the terrain surface is known throughout a scene, the geometric distortion it causes can be rectified. Since photogrammetry can be used to measure vertical as well as horizontal positions, it can be used to create a collection of vertical positions called a terrain model. Automated procedures for transforming vertical aerial photos into orthophotos require digital terrain models.
Since the early 1990s, orthophotos have been commonly used as sources for editing and revising of digital vector data.
15. Metadata
Through the remainder of this chapter and the next, we'll investigate the particular data products that comprise the framework themes of the U.S. National Spatial Data Infrastructure (NSDI). The format I'll use to discuss these data products reflects the Federal Geographic Data Committee's Metadata standard (FGDC, 1998c). Metadata is data about data. It is used to document the content, quality, format, ownership, and lineage of individual data sets. As the FGDC likes to point out, the most familiar example of metadata is the "Nutrition Facts" panel printed on food and drink labels in the United States. Metadata also provides the keywords needed to search for available data in specialized clearinghouses and in the World Wide Web.
Some of the key headings included in the FGDC metadata standard include:
- Identification Information: Who created the data, a brief description of its content, form, and purpose; its status, spatial extent, and use restrictions;
- Data Quality Information: Accuracy and completeness of attributes, horizontal and vertical positions, sources, and procedures used to create the data;
- Spatial Reference Information: Projection and/or coordinate system; datum and ellipsoid;
- Entity and Attribute Information: Feature and attribute categories used; and
- Distribution Information: Availability, and how to acquire the data.
FGDC's Content Standard for Digital Geospatial Metadata is published here. Geospatial professionals understand the value of metadata and know how to find it and how to interpret it.
16. Digital Orthophoto Quadrangle (DOQ)
Identification
Digital Orthophoto Quads (DOQs) are raster images of rectified aerial photographs. They are widely used as sources for editing and revising vector topographic data. For example, the vector roads data maintained by businesses like NAVTEQ and Tele Atlas, as well as local and state government agencies, can be plotted over DOQs, then edited to reflect changes shown in the orthoimage.
Most DOQs are produced by electronically scanning, then rectifying, black-and-white vertical aerial photographs. DOQ may also be produced from natural-color or near-infrared false-color photos, however, and from digital imagery. The variations in photo scale caused by relief displacement in the original images are removed by warping the image to compensate for the terrain elevations within the scene. Like USGS topographic maps, scale is uniform across each DOQ.
Most DOQs cover 3.75' of longitude by 3.75' of latitude. A set of four DOQs corresponds to each 7.5' quadrangle. (For this reason, DOQs are sometimes called DOQQs--Digital Orthophoto Quarter Quadrangles.) For its National Map, USGS has edge-matched DOQs into seamless data layers, by year of acquisition.

Data Quality
Like other USGS data products, DOQs conform to National Map Accuracy Standards. Since the scale of the series is 1:12,000, the standards warrant that 90 percent of well-defined points appear within 33.3 feet (10.1 meters) of their actual positions. One of the main sources of error is the rectification process, during which the image is warped such that each of a minimum of 3 control points matches its known location.
Spatial Reference Information
All DOQs are cast on the Universal Transverse Mercator projection used in the local UTM zone. Horizontal positions are specified relative to the North American Datum of 1983, which is based on the GRS 80 ellipsoid.
Entities and Attributes
The fundamental geometric element of a DOQ is the picture element (pixel). Each pixel in a DOQ corresponds to one square meter on the ground. Pixels in black-and-white DOQs are associated with a single attribute: a number from 0 to 255, where 0 stands for black, 255 stands for white, and the numbers in between represent levels of gray.
DOQs exceed the scanned topographic maps shown in Digital Raster Graphics (DRGs) in both pixel resolution and attribute resolution. DOQs are therefore much larger files than DRGs. Even though an individual DOQ file covers only one-quarter of the area of a topographic quadrangle (3.75 minutes square), it requires up to 55 Mb of digital storage. Because they cover only 25 percent of the area of topographic quadrangles, DOQs are also known as Digital Orthophoto Quarter Quadrangles (DOQQs).
Distribution
USGS DOQ files are in the public domain, and can be used for any purpose without restriction. They are available for free download from the USGS, or from various state and regional data clearinghouses as well as from the geoCOMMUNITY site. Digital orthoimagery data at 1-foot and 1-meter spatial resolution, collected from multiple sources, are available for user-specified areas, and even higher resolution imagery (HRO) data sets for certain areas are available from the National Map Viewer site.
To investigate DOQ data in greater depth, including links to a complete sample metadata document, visit Birthplace of the DOQ. FGDC's Content Standard for Digital Orthoimagery is published here.
Try This!
Explore DOQs with Global Mapper
Now it's time to use Global Mapper again, this time to investigate the characteristics of a set of USGS Digital Orthophoto (Quarter) Quadrangles. The instructions below assume that you have already installed the Global Mapper software on your computer. (If you haven't, return to Global Mapper installation instructions presented earlier in Chapter 6).
Note: Global Mapper is a Windows application and will not run under the Macintosh operating system.
- First, download one or more DOQ data archives. Each compressed DOQ is over 37 Mb in size and will take about 8 minutes to download via high speed DSL or cable, or over two hours via 56 Kbps modem.
- Next, decompress each archive into a directory on your hard disk.
- Open an archive (e.g., "DOQ_nw.zip").
- Create a subdirectory called "DOQ" within the directory in which you save data.
- Extract all files in the ZIP archive into your new subdirectory.
- Launch Global Mapper.
- Open a Digital Orthophoto (Quarter) Quadrangle by choosing File > Open Data File(s)..., then navigate to the subdirectory into which you extracted the DOQ data, then open the file 'bushkill_pa_nw.tif'.
- The trial version of Global Mapper allows you to open and view up to four files at once. Note that you can turn layers on and off, and even adjust their transparency at Tools > Control Center. You might find it interesting to open and compare the DOQ and DRG layers.
- Use the Zoom and Pan tools to magnify and scroll across the DOQ. The "Full View" button (house icon) refreshes the initial full view of the dataset.
- To view an excerpt of the DOQ metadata, navigate to Tools > Control Center, then click the Metadata button.

17. Summary
Many local, state, and federal government agencies produce and rely upon geographic data to support their day-to-day operations. The National Spatial Data Infrastructure (NSDI) is meant to foster cooperation among agencies to reduce costs and increase the quality and availability of public data in the U.S. The key components of NSDI include standards, metadata, data, a clearinghouse for data dissemination, and partnerships. The seven framework data themes have been described as "the data backbone of the NSDI" (FGDC, 1997, p. v). This chapter and the next review the origins, characteristics and status of the framework themes. In comparison with some other developed countries, framework data are fragmentary in the U.S., largely because mapping activities at various levels of government remain inadequately coordinated.
Chapter 6 considers two of the seven framework themes: geodetic control and orthoimagery. It discusses the impact of high-accuracy satellite positioning on accuracy standards for the National Spatial Reference System--the U.S.' horizontal and vertical control networks. The chapter stresses the fact that much framework data is derived, directly or indirectly, from aerial imagery. Geospatial professionals understand how photogrammetrists compile planimetrically-correct vector data by stereoscopic analysis of aerial imagery. They also understand how orthoimages are produced and used to help keep vector data current, among other uses.
The most ambitious attempt to implement a nationwide collection of framework data is the USGS' National Map. Composed of some of the digital data products described in this chapter and those that follow, the proposed National Map is to include high resolution (1 m) digital orthoimagery, variable resolution (10-30 m) digital elevation data, vector transportation, hydrography, and boundaries, medium resolution (30 m) land characterization data derived from satellite imagery, and geographic names. These data are to be seamless (unlike the more than 50,000 sheets that comprise the 7.5-minute topographic quadrangle series) and continuously updated. Meanwhile, in 2005, USGS announced that two of its three National Mapping Centers (in Reston, Virginia and Rolla, Missouri) would be closed, and over 300 jobs eliminated. Although funding for the Rolla center was subsequently restored by Congress, it remains to be seen whether USGS will be sufficiently resourced to fulfill its quest for a National Map.

18. Bibliography
Chapter 7: National Spatial Data Infrastructure II
1. Overview
Chapters 6 and 7 consider the origins and characteristics of the framework data themes that make up the United States' proposed National Spatial Data Infrastructure (NSDI). Chapter 6 discussed the geodetic control and orthoimagery themes. This chapter describes the origins, characteristics, and current status of the elevation, transportation, hydrography, governmental units, and cadastral themes.
Objectives
Students who successfully complete Chapter 7 should be able to:
- given a regular or irregular array of spot elevations, construct a triangulated irregular network, interpolate contour intervals and draw contour lines;
- compare vector and raster representations of terrain elevation;
- acquire and view digital elevation data from the National Elevation Dataset;
- calculate an interpolated spot elevation based on neighboring elevations;
- contrast the characteristics of three global elevation data products;
- describe the characteristics and current status of the NSDI hydrography, transportation, and governmental units themes as implemented in USGS' National Map; and
- interpret the size and relative location of a land parcel designated in terms of the U.S. Public Land Survey System.
"Try This!" Activities
Take a minute to complete any of the Try This activities that you encounter throughout the chapter. These are fun, thought provoking exercises to help you better understand the ideas presented in the chapter.

2. Theme: Elevation
The NSDI Framework Introduction and Guide (FGDC, 1997, p. 19) points out that "elevation data are used in many different applications." Civilian applications include flood plain delineation, road planning and construction, drainage, runoff, and soil loss calculations, and cell tower placement, among many others. Elevation data are also used to depict the terrain surface by a variety of means, from contours to relief shading and three-dimensional perspective views.
The NSDI Framework calls for an "elevation matrix" for land surfaces. That is, the terrain is to be represented as a grid of elevation values. The spacing (or resolution) of the elevation grid may vary between areas of high and low relief (i.e., hilly and flat). Specifically, the Framework Introduction states that
Elevation values will be collected at a post-spacing of 2 arc-seconds (approximately 47.4 meters at 40° latitude) or finer. In areas of low relief, a spacing of 1/2 arc-second (approximately 11.8 meters at 40° latitude) or finer will be sought (FGDC, 1997, p. 18).
The elevation theme also includes bathymetry--depths below water surfaces--for coastal zones and inland water bodies. Specifically,
For depths, the framework consists of soundings and a gridded bottom model. Water depth is determined relative to a specific vertical reference surface, usually derived from tidal observations. In the future, this vertical reference may be based on a global model of the geoid or the ellipsoid, which is the reference for expressing height measurements in the Global Positioning System (Ibid).
USGS has lead responsibility for the elevation theme. Elevation is also a key component of USGS' National Map. The next several pages consider how heights and depths are created, how they are represented in digital geographic data, and how they may be depicted cartographically.
3. Vector and Raster Approaches
The terms raster and vector were introduced back in Chapter 1 to denote two fundamentally different strategies for representing geographic phenomena. Both strategies involve simplifying the infinite complexity of the Earth's surface. As it relates to elevation data, the raster approach involves measuring elevation at a sample of locations. The vector approach, on the other hand, involves measuring the locations of a sample of elevations. I hope that this distinction will be clear to you by the end of this chapter.

Figure 7.4.1 compares how elevation data are represented in vector and raster data. On the left are elevation contours, a vector representation that is familiar with anyone who has used a USGS topographic map. The technical term for an elevation contour is isarithm, from the Greek words for "same" and "number." The terms isoline, isogram, and isopleth all mean more or less the same thing. (See any cartography text for the distinctions.)
As you will see later in this chapter, when you explore Digital Line Graph hypsography data using Global Mapper or dlgv 32 Pro, elevations in vector data are encoded as attributes of line features. The distribution of elevation points across the quadrangle is therefore irregular. Raster elevation data, by contrast, consist of grids of points at which elevation is encoded at regular intervals. Raster elevation data are what's called for by the NSDI Framework and the USGS National Map. Digital contours can now be rendered easily from raster data. However, much of the raster elevation data used in the National Map was produced from digital vector contours and hydrography (streams and shorelines). For this reason, we'll consider the vector approach to terrain representation first.
4. Contours
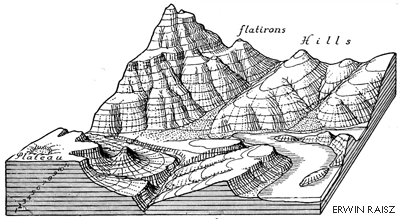
Drawing contour lines is a way to represent a terrain surface with a sample of elevations. Instead of measuring and depicting elevation at every point, you measure only along lines at which a series of imaginary horizontal planes slice through the terrain surface. The more imaginary planes, the more contours, and the more detail is captured.

Until photogrammetric methods came of age in the 1950s, topographers in the field sketched contours on the USGS 15-minute topographic quadrangle series. Since then, contours shown on most of the 7.5-minute quads were compiled from stereoscopic images of the terrain, as described in Chapter 6. Today, computer programs draw contours automatically from the spot elevations that photogrammetrists compile stereoscopically.
Although it is uncommon to draw terrain elevation contours by hand these days, it is still worthwhile to know how. In the next few pages, you'll have a chance to practice the technique, which is analogous to the way computers do it.
5. Contouring By Hand
This page will walk you through a methodical approach to rendering contour lines from an array of spot elevations (Rabenhorst and McDermott, 1989). To get the most from this demonstration, I suggest that you print the illustration in the attached image file. Find a pencil (preferably one with an eraser!) and straightedge, and duplicate the steps illustrated below. A "Try This!" activity will follow this step-by-step introduction, providing you a chance to go solo.
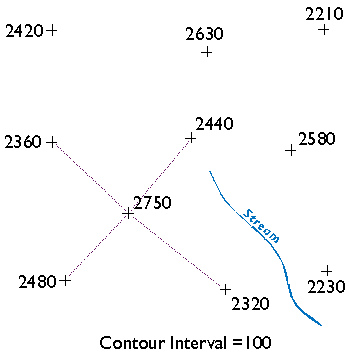
Starting at the highest elevation, draw straight lines to the nearest neighboring spot elevations. Once you have connected to all of the points that neighbor the highest point, begin again at the second highest elevation. (You will have to make some subjective decisions as to which points are "neighbors" and which are not.) Taking care not to draw triangles across the stream, continue until the surface is completely triangulated.
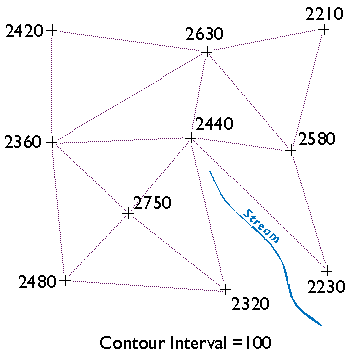
The result is a triangulated irregular network (TIN). A TIN is a vector representation of a continuous surface that consists entirely of triangular facets. The vertices of the triangles are spot elevations that may have been measured in the field by leveling, or in a photogrammetrist's workshop with a stereoplotter, or by other means. (Spot elevations produced photogrammetrically are called mass points.) A useful characteristic of TINs is that each triangular facet has a single slope degree and direction. With a little imagination and practice, you can visualize the underlying surface from the TIN even without drawing contours.
Wonder why I suggest that you not let triangle sides that make up the TIN cross the stream? Well, if you did, the stream would appear to run along the side of a hill, instead of down a valley as it should. In practice, spot elevations would always be measured at several points along the stream, and along ridges as well. Photogrammetrists refer to spot elevations collected along linear features as breaklines (Maune, 2007). I omitted breaklines from this example just to make a point.
You may notice that there is more than one correct way to draw the TIN. As you will see, deciding which spot elevations are "near neighbors" and which are not is subjective in some cases. Related to this element of subjectivity is the fact that the fidelity of a contour map depends in large part on the distribution of spot elevations on which it is based. In general, the density of spot elevations should be greater where terrain elevations vary greatly, and sparser where the terrain varies subtly. Similarly, the smaller the contour interval you intend to use, the more spot elevations you need.
(There are algorithms for triangulating irregular arrays that produce unique solutions. One approach is called Delaunay Triangulation which, in one of its constrained forms, is useful for representing terrain surfaces. The distinguishing geometric characteristic of a Delaunay triangulation is that a circle surrounding each triangle side does not contain any other vertex.)

Now draw ticks to mark the points at which elevation contours intersect each triangle side. For instance, see the triangle side that connects the spot elevations 2360 and 2480 in the lower left corner of Figure 7.6.3, above? One tick mark is drawn on the triangle where a contour representing elevation 2400 intersects. Now find the two spot elevations, 2480 and 2750, in the same lower left corner. Note that three tick marks are placed where contours representing elevations 2500, 2600, and 2700 intersect.
This step should remind you of the equal interval classification scheme you read about in Chapter 3. The right choice of contour interval depends on the goal of the mapping project. In general, contour intervals increase in proportion to the variability of the terrain surface. It should be noted that the assumption that elevations increase or decrease at a constant rate is not always correct, of course. We will consider that issue in more detail later.

Finally, draw your contour lines. Working downslope from the highest elevation, thread contours through ticks of equal value. Move to the next highest elevation when the surface seems ambiguous.
Keep in mind the following characteristics of contour lines (Rabenhorst and McDermott, 1989):
- Contours should always point upstream in valleys
- Contours should always point downridge along ridges
- Adjacent contours should always be sequential or equivalent
- Contours should never split into two
- Contours should never cross or loop
- Contours should never spiral
- Contours should never stop in the middle of a map
How does your finished map compare with the one I drew below?

Try This!
Now try your hand at contouring on your own. The purpose of this practice activity is to give you more experience in contouring terrain surfaces.
- First, view an image of an irregular array of 16 spot elevations.
- Print the image.
- Use the procedure outlined in this chapter to draw contour lines that represent the terrain surface that the spot elevations were sampled from. You may find this to be a moderately challenging task that takes about a half hour to do well. TIP: label the tick marks to make it easier to connect them.
- When finished, compare your result to an existing map.
Here are a couple of somewhat simpler problems and solutions in case you need a little more practice.
Practice Problem #1


Kevin Sabo (personal communication, Winter 2002) remarked that "If you were unfortunate enough to be hand-contouring data in the 1960's and 70's, you may at least have had the aid of a Gerber Variable Scale. After hand contouring in Chapter 7, I sure wished I had my Gerber!"

6. Digital Line Graph (DLG)
Identification
Digital Line Graphs (DLGs) are vector representations of most of the features and attributes shown on USGS topographic maps. Individual feature sets (outlined in the table below) are encoded in separate digital files. DLGs exist at three scales: small (1:2,000,000), intermediate (1:100,000) and large (1:24,000). Large-scale DLGs are produced in tiles that correspond to the 7.5-minute topographic quadrangles from which they were derived.
| Heading 1 | Heading 2 |
|---|---|
| Public Land Survey System (PLSS) | Township, range, and section lines |
| Boundaries | State, county, city, and other national and State lands such as forests and parks |
| Transportation | Roads and trails, railroads, pipelines and transmission lines |
| Hydrography | Flowing water, standing water, and wetlands |
| Hypsography | Contours and supplementary spot elevations |
| Non-vegetative features | Glacial moraine, lava, sand, and gravel |
| Survey control and markers | Horizontal and vertical monuments (third order or better) |
| Man-made features | Cultural features, such as building, not collected in other data categories |
| Woods, scrub, orchards, and vineyards | Vegetative surface cover |
Layers and contents of large-scale Digital Line Graph files. Not all layers available for all quadrangles (USGS, 2006).

Data quality
Like other USGS data products, DLGs conform to National Map Accuracy Standards. In addition, however, DLGs are tested for the logical consistency of the topological relationships among data elements. Similar to the Census Bureau's TIGER/Line, line segments in DLGs must begin and end at point features (nodes), and line segments must be bounded on both sides by area features (polygons).
Spatial Reference Information
DLGs are heterogenous. Some use UTM coordinates, others State Plane Coordinates. Some are based on NAD 27, others on NAD 83. Elevations are referenced either to NGVD 29 or NAVD 88 (USGS, 2006a).
Entities and attributes
The basic elements of DLG files are nodes (positions), line segments that connect two nodes, and areas formed by three or more line segments. Each node, line segment, and area is associated with two-part integer attribute codes. For example, a line segment associated with the attribute code "050 0412" represents a hydrographic feature (050), specifically, a stream (0412).
Distribution
Not all DLG layers are available for all areas at all three scales. Coverage is complete at 1:2,000,000. At the intermediate scale, 1:100,000 (30 minutes by 60 minutes), all hydrography and transportation files are available for the entire U.S., and complete national coverage is planned. At 1:24,000 (7.5 minutes by 7.5 minutes), coverage remains spotty. The files are in the public domain, and can be used for any purpose without restriction.
Large- and Intermediate -scale DLGs are available for download through EarthExplorer system. You used to be able to access 1:2,000,000 DLGs on-line at the USGS' National Atlas of the United States, but the National Atlas has recently been removed from service.
Digital Line Graph Hypsography
In one sense, DLGs are as much "legacy" data as the out-of-date topographic maps from which they were produced. Still, DLG data serve as primary or secondary sources for several themes in the USGS National Map, including hydrography, boundaries, and transportation. DLG hypsography data have not been included in the National Map, however. It was assumed that GIS users can generate elevation contours as needed from DEMs.

Hypsography refers to the measurement and depiction of the terrain surface, specifically with contour lines. Several different methods have been used to produce DLG hypsography layers, including:
- Scanning contour lines on photographic film or paper maps, converting the scanned raster data to vectors, then editing and attributing the vector features;
- Manually digitizing and attributing contour lines on photographic film or paper maps; and
- Producing contours by photogrammetric processes.
The preferred method is to manually digitize contour lines in vector mode, then to key-enter the corresponding elevation attribute data.

Try This!
Exploring DLGs with Global Mapper
Now, I'd like you to use the Global Mapper software to investigate the characteristics of the hypsography layer of a USGS Digital Line Graph (DLG). The instructions below assume that you have already installed the software on your computer. (If you have not done so, return to the download and installation instructions presented earlier in the Chapter 6, section 6 Try This! exercise). First you'll download a sample DLG file. In a following activity you'll have a chance to find and download DLG data for your area.
- If you haven't done so already, create a directory called "USGS Data" on your hard disk.materials.
- Next, Download the DLG.zip data archive. The ZIP archive is 1.2 Mb in size.
- Now, decompress the archive into a directory on your hard disk.
- Open the archive DLG.zip.
- Create a subdirectory called "DLG" within the directory in which you save data.
- Extract all files in the ZIP archive into your new subdirectory.
The end result will be five subdirectories, each of which includes the data files that make up a DLG "layer," along with a master directory.
- Launch Global Mapper.
- Open a Digital Line Graph by choosing File > Open Data Files..., then navigate to the directory "DLG/Hypso." Open the file Hp01catd.ddf. The data correspond with the 7.5 minute quadrangle for Bushkill, PA. The file is encoded in Spatial Data Transfer Standard (SDTS) format. For information about SDTS, see the SDTS Tutorial (PDF format).
- Experiment with Global Mapper's tools. Use Zoom and Pan to magnify and scroll across the DLG. The Full View button (the one with the house icon) refreshes the initial full view of the data set.
- The Feature Info tool allows you to query the attributes of a particular feature. Try clicking a single line segment. Note that you can display the attributes of a feature in the lower left portion of the application window by simply hovering over the feature.
- The Measure tool (ruler icon) allows you to not only measure distance as the crow flies, but also to see the area enclosed by a series of line segments drawn by repeated mouse clicks. Note again the location information that is given to you near the bottom of the application window.
- The trial version of Global Mapper allows you to open and view up to four files at once. You might find it interesting to open and compare the Bushkill DLG hypsography file and the corresponding DRG you viewed in Chapter 6. Note that you can turn layers on and off, and even adjust their transparency at Tools > Control Center.
How do the contours in the DLG compare with those in the DRG? What explains the difference?

7. Digital Elevation Model (DEM)
In general, a DEM is any raster representation of a terrain surface. Specifically, the U.S. Geological Survey produced a nation-wide DEM called the National Elevation Dataset (NED), which has traditionally served a primary source of elevation data. The NED has been incorporated into a newer elevation data product at the USGS called the 3D Elevation Program (3DEP). Here we consider the characteristics of traditional DEMs produced by the USGS. Later in this chapter, we'll consider sources of global terrain data.
Identification
USGS DEMs are raster grids of elevation values that are arrayed in series of south-north profiles. Like other USGS data, DEMs were produced originally in tiles that correspond to topographic quadrangles. Large-scale (7.5-minute and 15-minute), intermediate scale (30 minute), and small-scale (1 degree) series were produced for the entire U.S. The resolution of a DEM is a function of the east-west spacing of the profiles and the south-north spacing of elevation points within each profile.
DEMs corresponding to 7.5-minute quadrangles are available at 10-meter resolution for much, but not all, of the U.S. Coverage is complete at 30-meter resolution. In these large-scale DEMs, elevation profiles are aligned parallel to the central meridian of the local UTM zone, as shown in Figure 7.8.1, below. See how the DEM tile in the illustration below appears to be tilted? This is because the corner points are defined in unprojected geographic coordinates that correspond to the corner points of a USGS quadrangle. The farther the quadrangle is from the central meridian of the UTM zone, the more it is tilted.

As shown in Figure 7.8.2, the arrangement of the elevation profiles is different in intermediate- and small-scale DEMs. Like meridians in the northern hemisphere, the profiles in 30-minute and 1-degree DEMs converge toward the north pole. For this reason, the resolution of intermediate- and small-scale DEMs (that is to say, the spacing of the elevation values) is expressed differently than for large-scale DEMs. The resolution of 30-minute DEMs is said to be 2 arc seconds and 1-degree DEMs are 3 arc seconds. Since an arc second is 1/3600 of a degree, elevation values in a 3 arc-second DEM are spaced 1/1200 degree apart, representing a grid cell about 66 meters "wide" by 93 meters "tall" at 45º latitude.
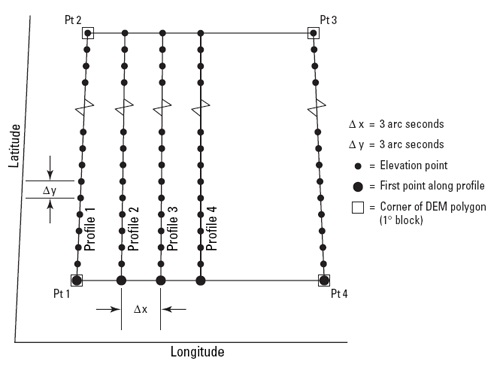
The preferred method for producing the elevation values that populate DEM profiles is interpolation from DLG hypsography and hydrography layers (including the hydrography layer enables analysts to delineate valleys with less uncertainty than hypsography alone). Some older DEMs were produced from elevation contours digitized from paper maps or during photogrammetric processing, then smoothed to filter out errors. Others were produced photogrammetrically from aerial photographs.
Data quality
The vertical accuracy of DEMs is expressed as the root mean square error (RMSE) of a sample of at least 28 elevation points. The target accuracy for large-scale DEMs is seven meters; 15 meters is the maximum error allowed.
Spatial Reference Information
Like DLGs, USGS DEMs are heterogenous. They are cast on the Universal Transverse Mercator projection used in the local UTM zone. Some DEMs are based upon the North American Datum of 1983, others on NAD 27. Elevations in some DEMs are referenced to either NGVD 29 or NAVD 88.
Entities and attributes
Each record in a DEM is a profile of elevation points. Records include the UTM coordinates of the starting point, the number of elevation points that follow in the profile, and the elevation values that make up the profile. Other than the starting point, the positions of the other elevation points need not be encoded, since their spacing is defined. (Later in this chapter, you'll download a sample USGS DEM file. Try opening it in a text editor to see what I'm talking about.)
Distribution
DEM tiles are available for free download through many state and regional clearinghouses. You can find these sources by searching the geospatial items on the Data.Gov site, formerly the separate Geospatial One Stop site.
As part of its National Map initiative, the USGS has developed a suite of elevation data products derived from traditional DEMs, lidar, and other sources. NED data are available at three resolutions: 1 arc second (approximately 30 meters), 1/3 arc second (approximately 10 meters), and 1/9 arc second (approximately 3 meters). Coverage ranges from complete at 1 arc second to extremely sparse at 1/9 arc second. As of 2020, USGS' elevation data products are managed through its 3D Elevation Program (3DEP). The second of the two following activities involves downloading 3DEP data and viewing it in Global Mapper.
Try This!
Exploring DEMs with Global Mapper
Global Mapper time again! This time, you'll investigate the characteristics of a USGS DEM. The instructions below assume that you have already installed the software on your computer. (If you haven't, return to installation instructions presented earlier in Chapter 6). The instructions will remind you how to open a DEM in Global Mapper.
- First, Download the DEM.zip data archive. The ZIP archive is 2.5 Mb in size. If you can't download the file, contact me right away so we can help you resolve the problem.
- Now, decompress the archive into a directory on your hard disk.
- Open the archive DEM.zip.
- Create a subdirectory called "DEM" within the directory in which you save data.
- Extract all files in the ZIP archive into your new subdirectory.
- Launch Global Mapper.
- Open a Digital Elevation Model by choosing File > Open Data File(s)..., then navigate to the directory DEM_30m or DEM_10m, then open the file bushkill_pa.dem
- Use the Zoom and Pan tools to magnify and scroll across the DEM. The Full View button (house icon) refreshes the initial full view of the dataset.
- To see the DEM data with(out) hill shading, find the Enable/Disable Hill Shading button (it has a sunburst in the lower left corner).
Enable hill shading. - You can also alter the appearance of the DEM by choosing Tools > Configure, and changing the settings in Vertical Options and Shader Options. Try this: on the Vertical Options tab select Gradient Shader from the pick list. Then, select the Shader Options tab and choose a color from each of the Low Color and High Color button in the Gradient Shader area. Hit the Apply button.
Go back to the Vertical Options tab and experiment with the Vertical Exaggeration slider. Hit Apply.
Try This!
Download your own National Elevation Dataset (NED) data
- Go to the National Map Download Tool.
- Navigate the map to zoom in on your hometown or other area of interest.
- Confirm that "Current Extent" is selected in the menu above the map. This specifies the area on the map for which you want to find data.
- Expand the "Elevation Products (3DEP)" section in the left-hand menu and check the box next to any dataset you'd like to download. (If given the option, specify to download the dataset in ArcGrid format.)
- Click the "Find Products" Button and use the links provided in the search results to show the footprint of each dataset on the map and to download your preferred DEM.
- A ZIP archive (.zip) will be created that you can save to your hard disk (e.g., "n45w100.zip"). Proceed to save the data file to your computer. The download process will take several seconds, depending upon your Internet download rate.
View the Dataset in Global Mapper
- Launch Global Mapper and navigate to where you saved the ZIP archive.
Double-click on the .zip file name. The data should display -- the software can read the data even in its compressed .zip form.
An image of the DEM data should appear in the Global Mapper window, similar to what you see shown below (even though the image below is from an older version of Global Mapper). If the Bushkill DEM is still visible, open the Control Center and uncheck the Bushkill DEM. Now click the Full View button (it is a picture of house) or click View > Full View. - To see the DEM data with(out) hill shading, find the Enable/Disable Hill Shading button on the Shader toolbar (it has a sunburst in the lower left corner).
Enable hill shading. - You can alter the appearance of the DEM by choosing Tools > Configure, and changing the settings in Vertical Options and Shader Options.
Try this: on the Vertical Options tab select Gradient Shader from the pick list. Then select the Shader Options tab and choose a color from each of the Low Color and High Color button in the Gradient Shader area. Hit the Apply button.
Go back to the Vertical Options tab and experiment with the Vertical Exaggeration slider. Hit Apply. - Again, you can view the metadata associated with the DEM data via the Tools > Control Center menu. Note the PIXEL dimensions reported in arc degrees, as opposed to something like meters.


8. Interpolation
DEMs are produced by various methods. The method preferred by USGS is to interpolate elevations grids from the hypsography and hydrography layers of Digital Line Graphs.

The elevation points in DLG hypsography files are not regularly spaced. DEMs need to be regularly spaced to support the slope, gradient, and volume calculations they are often used for. Grid point elevations must be interpolated from neighboring elevation points. In Figure 7.9.2 for example, the gridded elevations shown in purple were interpolated from the irregularly spaced spot elevations shown in red.

Here's another example of interpolation for mapping. The map below in Figure 7.9.3 shows how 1995 average surface air temperature differed from the average temperature over a 30-year baseline period (1951-1980). The temperature anomalies are depicted for grid cells that cover 3° longitude by 2.5° latitude.

The gridded data shown above were estimated from the temperature records associated with the very irregular array of 3,467 locations pinpointed in the map below. The irregular array is transformed into a regular array through interpolation. In general, interpolation is the process of estimating an unknown value from neighboring known values.

Elevation data are often not measured at evenly-spaced locations. Photogrammetrists typically take more measurements where the terrain varies the most. They refer to the dense clusters of measurements they take as "mass points." Topographic maps (and their derivatives, DLGs) are another rich source of elevation data. Elevations can be measured from contour lines, but obviously, contours do not form evenly-spaced grids. Both methods give rise to the need for interpolation.

The illustration above shows three number lines, each of which ranges in value from 0 to 10. If you were asked to interpolate the value of the tick mark labeled "?" on the top number line, what would you guess? An estimate of "5" is reasonable, provided that the values between 0 and 10 increase at a constant rate. If the values increase at a geometric rate, the actual value of "?" could be quite different, as illustrated in the bottom number line. The validity of an interpolated value depends, therefore, on the validity of our assumptions about the nature of the underlying surface.
As I mentioned in Chapter 1, the surface of the Earth is characterized by a property called spatial dependence. Nearby locations are more likely to have similar elevations than are distant locations. Spatial dependence allows us to assume that it's valid to estimate elevation values by interpolation.
Many interpolation algorithms have been developed. One of the simplest and most widely used (although often not the best) is the inverse distance weighted algorithm. Thanks to the property of spatial dependence, we can assume that estimated elevations are more similar to nearby elevations than to distant elevations. The inverse distance weighted algorithm estimates the value z of a point P as a function of the z-values of the nearest n points. The more distant a point, the less it influences the estimate.

The illustration shows how the elevation of a given point P can be estimated by averaging the known elevations of nearby points, while taking into account their distance from point P. The fancy technical term for the procedure is "inverse distance weighted interpolation."

9. Slope
Slope is a measure of change in elevation. It is a crucial parameter in several well-known predictive models used for environmental management, including the Universal Soil Loss Equation and agricultural non-point source pollution models.
One way to express slope is as a percentage. To calculate percent slope, divide the difference between the elevations of two points by the distance between them, then multiply the quotient by 100. The difference in elevation between points is called the rise. The distance between the points is called the run. Thus, percent slope equals (rise / run) x 100.

Another way to express slope is as a slope angle, or degree of slope. As shown below, if you visualize rise and run as sides of a right triangle, then the degree of slope is the angle opposite the rise. Since degree of slope is equal to the tangent of the fraction rise/run, it can be calculated as the arctangent of rise/run.

You can calculate slope on a contour map by analyzing the spacing of the contours. If you have many slope values to calculate, however, you will want to automate the process. It turns out that slope calculations are much easier to calculate for gridded elevation data than for vector data, since elevations are more or less equally spaced in raster grids.
Several algorithms have been developed to calculate percent slope and degree of slope. The simplest and most common is called the neighborhood method. The neighborhood method calculates the slope at one grid point by comparing the elevations of the eight grid points that surround it.

The neighborhood algorithm estimates percent slope at grid cell 5 (Z5) as the sum of the absolute values of east-west slope and north-south slope, and multiplying the sum by 100. Figure 7.10.4 illustrates how east-west slope and north-south slope are calculated. Essentially, east-west slope is estimated as the difference between the sums of the elevations in the first and third columns of the 3 x 3 matrix. Similarly, north-south slope is the difference between the sums of elevations in the first and third rows (note that in each case the middle value is weighted by a factor of two).

The illustration shows how the terrain slope at a given elevation grid cell can be calculated from elevations of the eight grid cells that surround it. First, north-south slope is calculated from the grid columns. Then east-west slope is calculated from the grid rows. The square root of the sum of the north-south slope and east-west slope, multiplied by 100, equals the percent slope at the original grid cell. The fancy technical term for the procedure is "neighborhood algorithm."
The neighborhood algorithm calculates slope for every cell in an elevation grid by analyzing each 3 x 3 neighborhood. Percent slope can be converted to slope degree later. The result is a grid of slope values suitable for use in various soil loss and hydrologic models.
10. Relief Shading
You can see individual pixels in the zoomed image of a 7.5-minute DEM below. I used dlgv32 Pro's "Gradient Shader" to produce the image. Each pixel represents one elevation point. The pixels are shaded through 256 levels of gray. Dark pixels represent low elevations, light pixels represent high ones.

It's also possible to assign gray values to pixels in ways that make it appear that the DEM is illuminated from above. The image below, which shows the same portion of the Bushkill DEM as the image above, illustrates the effect, which is called terrain shading, hill shading, or shaded relief.

The appearance of a shaded terrain image depends on several parameters, including vertical exaggeration. Compare the four terrain images of North America shown below, in which elevations are exaggerated 5 times, 10 times, 20 times, and 40 times respectively.

Another influential parameter is the angle of illumination. Compare terrain images that have been illuminated from the northeast, southeast, southwest, and northwest. Does the terrain appear to be inverted in one or more of the images? To minimize the possibility of terrain inversion, it is conventional to illuminate terrain from the northwest.

11. Lidar
For many applications, 30-meter DEMs whose vertical accuracy is measured in meters are simply not detailed enough. Greater accuracy and higher horizontal resolution can be produced by photogrammetric methods, but precise photogrammetry is often too time-consuming and expensive for extensive areas. Lidar is a digital remote sensing technique that provides an attractive alternative.
Lidar stands for LIght Detection And Ranging. Like radar (RAdio Detecting And Ranging), lidar instruments transmit and receive energy pulses, and enable distance measurement by keeping track of the time elapsed between transmission and reception. Instead of radio waves, however, lidar instruments emit laser light (laser stands for Light Amplifications by Stimulated Emission of Radiation).
Lidar instruments are typically mounted in low altitude aircraft. They emit up to 5,000 laser pulses per second, across a ground swath some 600 meters wide (about 2,000 feet). The ground surface, vegetation canopy, or other obstacles reflect the pulses, and the instrument's receiver detects some of the backscatter. Lidar mapping missions rely upon GPS to record the position of the aircraft, and upon inertial navigation instruments (gyroscopes that detect an aircraft's pitch, yaw, and roll) to keep track of the system's orientation relative to the ground surface.
In ideal conditions, lidar can produce DEMs with 15-centimeter vertical accuracy, and horizontal resolution of a few meters. Lidar applications in topographic mapping, forestry, corridor mapping, and 3-D building modeling are discussed in detail in the open-access courseware for GEOG 481: Topographic Mapping with Lidar. Illustrated below is a scientific application in which lidar was used successfully to detect subtle changes in the thickness of the Greenland ice sheet that result in a net loss of over 50 cubic kilometers of ice annually.

To learn more about the use of lidar in mapping changes in the Greenland ice sheet, visit NASA’s Scientific Visualization Studio.
12. Global Elevation Data
This page profiles three data products that include elevation (and, in one case, bathymetry) data for all or most of the Earth's surface.
ETOPO1
ETOPO1 is a digital elevation model that includes both topography and bathymetry for the entire world. It consists of more than 233 million elevation values which are regularly spaced at 1 minute of latitude and longitude. At the equator, the horizontal resolution of ETOPO1 is approximately 1.85 kilometers. Vertical positions are specified in meters, and there are two versions of the dataset: one with elevations at the “Ice Surface" of the Greenland and Antarctic ice sheets, and one with elevations at “Bedrock" beneath those ice sheets. Horizontal positions are specified in geographic coordinates (decimal degrees). Source data, and thus data quality, vary from region to region.
You can download ETOPO1 data from the National Geophysical Data Center.
GTOPO30

GTOPO30 is a digital elevation model that extends over the world's land surfaces (but not under the oceans). GTOPO30 consists of more than 2.5 million elevation values, which are regularly spaced at 30 seconds of latitude and longitude. At the equator, the resolution of GTOPO30 is approximately 0.925 kilometers -- two times greater than ETOPO1. Vertical positions are specified to the nearest meter, and horizontal positions are specified in geographic coordinates. GTOPO30 data are distributed as tiles, most of which are 50° in latitude by 40° in longitude.
GTOPO30 tiles are available for download from USGS' EROS Data Center.
Shuttle Radar Topography Mission (SRTM)
From February 11 to February 22, 2000, the space shuttle Endeavor bounced radar waves off the Earth's surface, and recorded the reflected signals with two receivers spaced 60 meters apart. The mission measured the elevation of land surfaces between 60° N and 56° S latitude. The National Aeronautics and Space Administration (NASA) and Jet Propulsion Laboratory (JPL) produced two SRTM data products—one at 1 arc-second resolution (about 30 meters), another at 3 arc-seconds (about 90 meters). Initially, access to the 30 meter SRTM data was restricted by the National Geospatial-Intelligence Agency (NGA), which sponsored the project along with NASA. However, in 2014 the White House announced at the U.N. Climate Summit that the high resolution SRTM data would be released globally over the coming year.
More information about the announcement, and about SRTM data, is available at JPL's SRTM site.

Figure 7.13.3 shows Viti Levu, the largest of the some 332 islands that comprise the Sovereign Democratic Republic of the Fiji Islands. Viti Levu's area is 10,429 square kilometers (about 4000 square miles). Nakauvadra, the rugged mountain range running from north to south, has several peaks rising above 900 meters (about 3000 feet). Mount Tomanivi, in the upper center, is the highest peak at 1324 meters (4341 feet).
13. Bathymetry
The term bathymetry refers to the process and products of measuring the depth of water bodies. The U.S. Congress authorized the comprehensive mapping of the nation's coasts in 1807, and directed that the task be carried out by the federal government's first science agency, the Office of Coast Survey (OCS). That agency is now responsible for mapping some 3.4 million nautical square miles encompassed by the 12-mile territorial sea boundary, as well as the 200-mile Exclusive Economic Zone claimed by the U.S., a responsibility that entails regular revision of about 1,000 nautical charts. The coastal bathymetry data that appears on USGS topographic maps, like the one shown below, is typically compiled from OCS charts.

Early hydrographic surveys involved sampling water depths by casting overboard ropes weighted with lead and marked with depth intervals called marks and deeps. Such ropes were called leadlines for the weights that caused them to sink to the bottom. Measurements were called soundings. By the late 19th century, piano wire had replaced rope, making it possible to take soundings of thousands rather than just hundreds of fathoms (a fathom is six feet).

Echo sounders were introduced for deepwater surveys beginning in the 1920s. Sonar (SOund NAvigation and Ranging) technologies have revolutionized oceanography in the same way that aerial photography revolutionized topographic mapping. The seafloor topography revealed by sonar and related shipborne remote sensing techniques provided evidence that supported theories about seafloor spreading and plate tectonics.
Below is an artist's conception of an oceanographic survey vessel operating two types of sonar instruments: multibeam and side scan sonar. On the left, a multibeam instrument mounted in the ship's hull calculates ocean depths by measuring the time elapsed between the sound bursts it emits and the return of echoes from the seafloor. On the right, side scan sonar instruments are mounted on both sides of a submerged "towfish" tethered to the ship. Unlike multibeam, side scan sonar measures the strength of echoes, not their timing. Instead of depth data, therefore, side scanning produces images that resemble black-and-white photographs of the seafloor.

14. Statistical Surfaces
Strategies used to represent terrain surfaces can be used for other kinds of surfaces as well. For example, one of my first projects here at Penn State was to work with a distinguished geographer, the late Peter Gould, who was studying the diffusion of the Acquired Immune Deficiency Syndrome (AIDS) virus in the United States. Dr. Gould had recently published the map below.

Below are the cities with the most AIDS cases in the U.S in 1988:
- San Francisco
- New York
- Los Angeles
- Washington DC
- Houston
- Miami
- Boston
Gould portrayed the distribution of disease in the same manner as another geographer might portray a terrain surface. The portrayal is faithful to Gould's conception of the contagion as a continuous phenomenon. It was important to Gould that people understood that there was no location that did not have the potential to be visited by the epidemic. For both the AIDS surface and a terrain surface, a quantitative attribute (z) exists for every location (x,y). In general, when a continuous phenomenon is conceived as being analogous to the terrain surface, the conception is called a statistical surface.
15. Theme: Hydrography
The NSDI Framework Introduction and Reference (FGDC, 1997) envisions the hydrography theme in this way:
Framework hydrography data include surface water features such as lakes and ponds, streams and rivers, canals, oceans, and shorelines. Each of these features has the attributes of a name and feature identification code. Centerlines and polygons encode the positions of these features. For feature identification codes, many federal and state agencies use the Reach schedule developed by the U.S. Environmental Protection Agency (EPA).
Many hydrography data users need complete information about connectivity of the hydrography network and the direction in which the water flows encoded in the data. To meet these needs, additional elements representing flows of water and connections between features may be included in framework data (p. 20).
Identification
FGDC had the National Hydrography Dataset (NHD) in mind when they wrote this description. NHD combines the vector features of Digital Line Graph (DLG) hydrography with the EPA’s Reach files. Reaches are segments of surface water that share similar hydrologic characteristics. Reaches are of three types: transport, coastline, and waterbody. DLG lines features represent the transport and coastline types; polygon features are used to represent waterbodies. Every reach segment in the NHD is assigned a unique reach code, along with a host of other hydrological attributes including stream flow direction (which is encoded in the digitizing order of nodes that make up each segment), network connectivity, and feature names, among others. Because the order of reach codes are sequential from reach to reach, point-source data (such as a pollutant spill) can be geocoded to the affected reach. Used in this way, reaches comprise a linear referencing system comparable to postal addresses along streets (USGS, 2002).

| Common Identifier for First Reach | Common Identifier for Second Reach | Direction Description |
|---|---|---|
| 1 | 2 | In |
| 4 | 2 | In |
| 6 | 5 | In |
| 5 | 3 | In |
| 2 | 3 | In |
| 0 | 1 | Network Start |
| 0 | 4 | Network Start |
| 0 | 6 | Network Start |
| 0 | 5 | Network Start |
| 3 | 0 | Network End |
NHD parses the U.S. surface drainage network into four hierarchical categories of units: 21 Regions, 222 Subregions, 352 Accounting units, and 2150 Cataloging units (also called Watersheds). Features can exist at multiple levels of the hierarchy, though they might not be represented in the same way. For example, while it might make the most sense to represent a given stream as a polygon features at the Watershed level, it may be more aptly represented as a line feature at the Region or Subregion level. NHD supports this by allowing multiple features to share the same reach codes. Another distinctive feature of NHD is artificial flowlines--centerline features that represent paths of water flow through polygon features such as standing water bodies. NHD is complex because it is designed to support sophisticated hydrologic modeling tasks, including point-source pollution modeling, flood potential, bridge construction, among others (Ralston, 2004).

NHD are available at three levels of detail (scale): medium (1:100,000, which is available for the entire U.S.), high (1:24,000, production of which is underway, “according to the availability of matching resources from NHD partners” (USGS, 2002, p. 2), and local (larger scales such as 1:5,000), which "is being developed where partners and data exist" for select areas (USGS, 2006c; USGS, 2009; USGS 2013).
Spatial Reference Information
NHD coordinates are decimal degrees referenced to the NAD 83 horizontal datum.
Distribution
Try This!
Download and view an extract from the National Hydrography Dataset
- Visit the USGS's National Map Download site.
- Navigate the map to zoom in on your area of interest.
- Confirm that "Current Extent" is selected in the menu above the map. This specifies the area on the map for which you want to find data.
- Expand the "Hydrography (NHD) and Watersheds (WBD)" section in the left-hand menu and check the box next to any dataset you'd like to download. (If given the option, specify to download the dataset in shapefile format.) If you were working in ArcGIS, you could choose the File Geodatabase option. Ralston (2004, p.187) observes that NHD "is precisely the type of information that could benefit from an integrated data model in an object relational database."
- Click the "Find Products" Button and use the links provided in the search results to show the footprint of each dataset on the map and to download your preferred dataset.
- A ZIP archive (.zip) will be created that you can save to your hard disk (e.g., "n45w100.zip"). Proceed to save the data file to your computer. The download process will take several seconds, depending upon your Internet download rate.
- After you retrieve your data set open Global Mapper and navigate to where you saved the ZIP archive.
Double-click on the .zip file name. The data should display -- the software can read the data even in its compressed .zip form. - Use the Feature Info Tool pointer tool (the icon that looks like a blue-filled circle with an "i" in it) to reveal attributes of the reaches. In the example below, I have highlighted a flowline associated with Cedar Creek in western Michigan.


16. Theme: Transportation
Transportation network data are valuable for all sorts of uses, including two we considered in Chapter 4: geocoding and routing. The Federal Geographic Data Committee (1997, p.19) specified the following vector features and attributes for the transportation framework theme:
| FEATURE | ATTRIBUTES |
|---|---|
| Roads | Centerlines, feature identification code (using linear referencing systems where available), functional class, name (including route numbers), and street address ranges |
| Trails | Centerlines, feature identification code (using linear referencing systems where available), name, and type |
| Railroads | Centerlines, feature identification code (using linear referencing systems where available), and type |
| Waterways | Centerlines, feature identification code (using linear referencing systems where available), and name |
| Airports and ports | Feature identification code and name |
| Bridges and tunnels | Feature identification code and name |
Identification
As part of the National Map initiative, USGS and partners are developing a comprehensive national database of vector transportation data. The transportation theme "includes best available data from Federal partners such as the Census Bureau and the Department of Transportation, State and local agencies" (USGS, 2007).
As envisioned by FGDC, centerlines are used to represent transportation routes. Like the lines painted down the middle of two-way streets, centerlines are 1-dimensional vector features that approximate the locations of roads, railroads, and navigable waterways. In this sense, road centerlines are analogous to the flowpaths encoded in the National Hydrologic Dataset (see previous page). Also like the NHD (and TIGER), road topology must be encoded to facilitate analysis of transportation networks.
To get a sense of the complexity of the features and attributes that comprise the transportation theme, see the Transportation Data Model (This is a 36" x 48" poster in a 5.2 Mb PDF file.) [The link to the Transportation Data Model poster recently became disconnected. Instead look at the model diagrams in the Part 7: Transportation Base of the FGDC Geographic Framework Data Content Standard.]
In the U.S. at least, the best road centerline data is produced commercial firms including HERE and Tele Atlas, which license data to manufacturers of in-car GPS navigation systems, and Google and Apple. Because these data are proprietary, however, USGS must look elsewhere for data that can be made available for public use. TIGER/Line data produced by the Census Bureau will likely play an important role after the TIGER/MAF Modernization project is complete (see Chapter 4).
Distribution
Try This!
View and download National Map transportation data
- Access the National Map Viewer.
- In the Layers menu, check the box for the Transportation layer. You can expand the Transportation list and sub-select different layers.
- As you zoom in to larger map scales (using the slider bar at the upper-left of the map), additional transportation layers will become visible.
- The USGS National Transportation Database is available for download at Data.gov.

17. Theme: Governmental Units
The FGDC framework also includes boundaries of governmental units, including:
- Nation
- States and statistically equivalent areas
- Counties and statistically equivalent areas
- Incorporated places and consolidated cities
- Functioning legal minor civil divisions
- Federal- or state-recognized American Indian reservations and trustlands
- Alaska native regional corporations
FGDC specifies that:
Each of these features includes the attributes of name and the applicable Federal Information Processing Standard (FIPS) code. Features boundaries include information about other features (such as road, railroads, or streams) with which the boundaries are associated and a description of the association (such as coincidence, offset, or corridor. (FGDC, 1997, p. 20-21)
Identification
The USGS National Map aspires to include a comprehensive database of boundary data. In addition to the entities outlined above, the National Map also lists congressional districts, school districts, and ZIP Code zones. Sources for these data include "Federal partners such as the U.S. Census Bureau, other Federal agencies, and State and local agencies." (USGS, 2007).
To get a sense of the complexity of the features and attributes that comprise this theme, see the Governmental Units Data Model (This is a 36" x 48" poster in a 2.4 Mb PDF file.) [The link to the Governmental Units Data Model poster recently became disconnected. Instead look at the model diagrams in Part 5: Governmental unit and other geographic area boundaries of the FGDC Geographic Framework Data Content Standard.]
Distribution
Try This!
View and download National Map governmental units data
- Access the Viewer here.
- Expand the pane containing the layer options by clicking on Overlays at the upper-left.
- Under Base Data Layers, check the box for the Governmental Unit Boundaries. You can expand this list and sub-select different boundary layers.
- As you zoom into larger map scales (using the slider bar at the upper-left of the map), additional boundary layers will become visible.
- If you wish to download an extract from the Governmental Unit Boundaries database, visit the National Map Download site and access the "Boundaries - National Boundary Dataset" section.

18. Theme: Cadastral
FGDC (1997, p. 21) points out that:
Cadastral data represent the geographic extent of the past, current, and future rights and interests in real property. The spatial information necessary to describe the geographic extent and the rights and interests includes surveys, legal description reference systems, and parcel-by-parcel surveys and descriptions.
However, no one expects that legal descriptions and survey coordinates of private property boundaries (as depicted schematically in the portion of the plat map shown below) will be included in the USGS National Map any time soon. As discussed at the outset of Chapter 6, this is because local governments have authority for land title registration in the U.S., and most of these governments have neither the incentive nor the means to incorporate such data into a publicly-accessible national database.

FGDC's modest goal for the cadastral theme of the NSDI framework is to include:
...cadastral reference systems, such as the Public Land Survey System (PLSS) and similar systems not covered by the PLSS ... and publicly administered parcels, such as military reservations, national forests, and state parks. (Ibid, p. 21)
FGDC's Cadastral Data Content Standard is published here.
The colored areas on the map below show the extent of the United States Public Land Surveys, which commenced in 1784 and took nearly a century to complete (Muehrcke and Muehrcke, 1998). The purpose of the surveys was to partition "public land" into saleable parcels in order to raise revenues needed to retire war debt, and to promote settlement. A key feature of the system is its nomenclature, which provides concise, unique specifications of the location and extent of any parcel.

Each Public Land Survey (shown in the colored areas above) commenced from an initial point at the precisely surveyed intersection of a base line and principal meridian. Surveyed lands were then partitioned into grids of townships each approximately six miles square.

Townships are designated by their locations relative to the base line and principal meridian of a particular survey. For example, the township highlighted in gold above is the second township south of the baseline and the third township west of the principal meridian. The Public Land Survey designation for the highlighted township is "Township 2 South, Range 3 West." Because of this nomenclature, the Public Land Survey System is also known as the "township and range system." Township T2S, R3W is shown enlarged below.

Townships are subdivided into grids of 36 sections. Each section covers approximately one square mile (640 acres). Notice the back-and-forth numbering scheme. Section 14, highlighted in gold above in Figure 7.19.4, is shown enlarged below in Figure 7.19.5.

Individual property parcels are designated as shown in Figure 7.19.5. For instance, the NE 1/4 of Section 14, Township 2 S, Range 3W, is a 160-acre parcel. Public Land Survey designations specify both the location of a parcel and its area.

The influence of the Public Land Survey grid is evident in the built environment of much of the American Midwest. As Mark Monmonier (1995, p. 114) observes:
The result [of the U.S. Public Land Survey] was an 'authored landscape' in which the survey grid had a marked effect on settlement patterns and the shapes of counties and smaller political units. In the typical Midwestern county, roads commonly following section lines, the rural population is dispersed rather than clustered, and the landscape has a pronounced checkerboard appearance.
19. Summary
NSDI framework data represent "the most common data themes [that] users need" (FGDC, 1997, p. 3), including geodetic control, orthoimagery, elevation, hydrography, transportation, governmental unit boundaries, and cadastral reference information. Some themes, like transportation and governmental units, represent things that have well-defined edges. In this sense, we can think of things like roads and political boundaries as discrete phenomena. The vector approach to geographic representation is well suited to digitizing discrete phenomena. Line features do a good job of representing roads, for example, and polygons are useful approximations of boundaries.
As you recall from Chapter 1, however, one of the distinguishing properties of the Earth's surface is that it is continuous. Some phenomena distributed across the surface are continuous too. Terrain elevations, gravity, magnetic declination and surface air temperature can be measured practically everywhere. For many purposes, raster data are best suited to representing continuous phenomena.
An implication of continuity is that there is an infinite number of locations at which phenomena can be measured. It is not possible, obviously, to take an infinite number of measurements. Even if it were, the mass of data produced would not be usable. The solution, of course, is to collect a sample of measurements and to estimate attribute values for locations that are left unmeasured. Chapter 7 also considers how missing elevations in a raster grid can be estimated from existing elevations, using a procedure called interpolation. The inverse distance weighted interpolation procedure relies upon another fundamental property of geographic data, spatial dependence.
The chapter concludes by investigating the characteristics and current status of the hydrography, transportation, governmental units, and cadastral themes. You had the opportunity to access, download, and open several of the data themes using viewers provided by USGS as part of its National Map initiative. In general, you should have found that although neither the NSDI or National Map visions have been fully realized, substantial elements of each is in place. Further progress depends on the American public's continuing commitment to public data, and to the political will of our representatives in government.

20. Bibliography
Chapter 8: Remotely Sensed Image Data
1. Overview
Chapter 7 concluded with the statement that the raster approach is well suited not only to terrain surfaces but to other continuous phenomena as well. This chapter considers the characteristics and uses of raster data produced with airborne and satellite remote sensing systems. Remote sensing is a key source of data for land use and land cover mapping, agricultural and environmental resource management, mineral exploration, weather forecasting, and global change research.
Summarizing the entirety of remote sensing in a single brief chapter is a daunting task. You may know that the Penn State Online Geospatial Education program offers a four-course remote sensing curriculum. This introduction is meant to familiarize you with the remote sensing-related competencies included in the U.S. Department of Labor's Geospatial Technology Competency Model. If the chapter interests you, consider enrolling in one or more of the specialized remote sensing courses if your schedule permits.
Objectives
The overall goal of the chapter is to acquaint you with the properties of data produced by airborne and satellite-based sensors. Specifically, students who successfully complete Chapter 8 should be able to:
- identify the common characteristics and sources of remotely sensed image data;
- demonstrate familiarity with trends in remote sensing technologies, methods, and organizations;
- explain why and how remotely sensed image data are processed; and
- identify examples of active and passive remote sensing systems and applications.
"Try This!" Activities
Take a minute to complete any of the Try This activities that you encounter throughout the chapter. These are fun, thought provoking exercises to help you better understand the ideas presented in the chapter.

2. Nature of Remotely Sensed Image Data
Data consist of measurements. Here we consider the nature of the phenomenon that many, though not all, remote sensing systems measure: electromagnetic energy. Many of the objects that make up the Earth's surface reflect and emit electromagnetic energy in unique ways. The appeal of multispectral remote sensing is that objects that are indistinguishable at one energy wavelength may be easy to tell apart at other wavelengths. You will see that digital remote sensing is a little like scanning a paper document with a desktop scanner, only a lot more complicated.
(Just for fun: Can you think of a remote sensing technology that does not measure electromagnetic energy? We'll name one in the last page of this chapter.)
3. Electromagnetic Spectrum
Most remote sensing instruments measure the same thing: electromagnetic radiation. Electromagnetic radiation is a form of energy emitted by all matter above absolute zero temperature (0 Kelvin or -273° Celsius). X-rays, ultraviolet rays, visible light, infrared light, heat, microwaves, and radio and television waves are all examples of electromagnetic energy.

The graph above shows the relative amounts of electromagnetic energy emitted by the Sun and the Earth across the range of wavelengths called the electromagnetic spectrum. Values along the horizontal axis of the graph range from very short wavelengths (ten-millionths of a meter) to long wavelengths (meters). Note that the horizontal axis is logarithmically scaled so that each increment represents a ten-fold increase in wavelength. The axis has been interrupted three times at the long wave end of the scale to make the diagram compact enough to fit on your screen. The vertical axis of the graph represents the magnitude of radiation emitted at each wavelength.
Hotter objects radiate more electromagnetic energy than cooler objects. Hotter objects also radiate energy at shorter wavelengths than cooler objects. Thus, as the graph shows, the Sun emits more energy than the Earth, and the Sun's radiation peaks at shorter wavelengths. The portion of the electromagnetic spectrum at the peak of the Sun's radiation is called the visible band because the human visual perception system is sensitive to those wavelengths. Human vision is a powerful means of sensing electromagnetic energy within the visual band. Remote sensing technologies extend our ability to sense electromagnetic energy beyond the visible band, allowing us to see the Earth's surface in new ways, which, in turn, reveals patterns that are normally invisible.

The graph above names several regions of the electromagnetic spectrum. Remote sensing systems have been developed to measure reflected or emitted energy at various wavelengths for different purposes. This chapter highlights systems designed to record radiation in the bands commonly used for land use and land cover mapping: the visible, infrared, and microwave bands.

At certain wavelengths, the atmosphere poses an obstacle to satellite remote sensing by absorbing electromagnetic energy. Sensing systems are therefore designed to measure wavelengths within the windows where the transmissivity of the atmosphere is greatest.
4. Spectral Response Patterns
The Earth's land surface reflects about three percent of all incoming solar radiation back to space. The rest is either reflected by the atmosphere or absorbed and re-radiated as infrared energy. The various objects that make up the surface absorb and reflect different amounts of energy at different wavelengths. The magnitude of energy that an object reflects or emits across a range of wavelengths is called its spectral response pattern.
The graph below illustrates the spectral response patterns of water, brownish gray soil, and grass between about 0.3 and 6.0 micrometers. The graph shows that grass, for instance, reflects relatively little energy in the visible band (although the spike in the middle of the visible band explains why grass looks green). Like most vegetation, the chlorophyll in grass absorbs visible energy (particularly in the blue and red wavelengths) for use during photosynthesis. About half of the incoming near-infrared radiation is reflected, however, which is characteristic of healthy, hydrated vegetation. Brownish gray soil reflects more energy at longer wavelengths than grass. Water absorbs most incoming radiation across the entire range of wavelengths. Knowing their typical spectral response characteristics, it is possible to identify forests, crops, soils, and geological formations in remotely sensed imagery, and to evaluate their condition.

The next graph demonstrates one of the advantages of being able to see beyond the visible spectrum. The two lines represent the spectral response patterns of conifer and deciduous trees. Notice that the reflectances within the visual band are nearly identical. At longer, near- and mid-infrared wavelengths, however, the two types are much easier to differentiate. Land use and land cover mapping were previously accomplished by visual inspection of photographic imagery. Multispectral data and digital image processing make it possible to partially automate land cover mapping, which, in turn, makes it cost effective to identify some land use and land cover categories automatically, all of which makes it possible to map larger land areas more frequently.

Spectral response patterns are sometimes called spectral signatures. This term is misleading, however, because the reflectance of an entity varies with its condition, the time of year, and even the time of day. Instead of thin lines, the spectral responses of water, soil, grass, and trees might better be depicted as wide swaths to account for these variations.
5. Raster Scanning
Remote sensing systems commonly work in much the same way as the digital scanner you may have attached to your personal computer. Scanners like the one pictured below create a digital image of an object by recording, pixel by pixel, the intensity of light reflected from the object. The component that measures reflectance is called the scan head, which consists of a row of tiny sensors that convert light to electrical charges. Color scanners may have three light sources and three sets of sensors, one each for the blue, green, and red wavelengths of visible light. When you push a button to scan a document, the scan head is propelled rapidly across the image, one small step at a time, recording new rows of electrical signals as it goes. Remotely sensed data, like the images produced by your desktop scanner, consist of reflectance values arrayed in rows and columns that make up raster grids.

After the scan head converts reflectances to electrical signals, another component, called the analog-to-digital converter, converts the electrical charges into digital values. Although reflectances may vary from 0 percent to 100 percent, digital values typically range from 0 to 255. This is because digital values are stored as units of memory called bits. One bit represents a single binary integer, 1 or 0. The more bits of data that are stored for each pixel, the more precisely reflectances can be represented in a scanned image. The number of bits stored for each pixel is called the bit depth of an image. An 8-bit image is able to represent 28 (256) unique reflectance values. A color desktop scanner may produce 24-bit images in which 8 bits of data are stored for each of the blue, green, and red wavelengths of visible light.

As you might imagine, scanning the surface of the Earth is considerably more complicated than scanning a paper document with a desktop scanner. Unlike the document, the Earth's surface is too large to be scanned all at once, and so must be scanned piece by piece, and mosaicked together later. Documents are flat, but the Earth's shape is curved and complex. Documents lie still while they are being scanned, but the Earth rotates continuously around its axis at a rate of over 1,600 kilometers per hour. In the desktop scanner, the scan head and the document are separated only by a plate of glass; satellite-based sensing systems may be hundreds or thousands of kilometers distant from their targets, separated by an atmosphere that is nowhere near as transparent as glass. And while a document in a desktop scanner is illuminated uniformly and consistently, the amount of solar energy reflected or emitted from the Earth's surface varies with latitude, the time of year, and even the time of day. All of these complexities combine to yield data with geometric and radiometric distortions that must be corrected before the data are used for analysis. Later in this chapter, we'll discuss some of the image processing techniques that are used to correct remotely sensed image data.
6. Resolution
So far, you've read that remote sensing systems measure electromagnetic radiation, and that they record measurements in the form of raster image data. The resolution of remotely sensed image data varies in several ways. As you recall, resolution is the least detectable difference in a measurement. In this context, four of the most important kinds are spatial, radiometric, spectral, and temporal resolution.
Spatial resolution refers to the coarseness or fineness of a raster grid. It is sometimes expressed as ground sample distance (GSD), the nominal dimension of a single side of a square pixel measured in ground units. High-resolution data, such as those produced by digital aerial imaging or by the Quickbird satellite, have GSDs of one meter or less. Moderate-resolution data, such as those produced by Landsat sensors, have GSDs of about 15-100 meters. Sensors with low spatial resolution like AVHRR and MODIS sensors produce images with GSDs measured in hundreds of meters.

The higher the spatial resolution of a digital image, the more detail it contains. Detail is valuable for some applications, but it is also costly. Consider, for example, that an 8-bit image of the entire Earth whose spatial resolution is one meter could fill 78,400 CD-ROM disks, a stack over 250 feet high (assuming that the data were not compressed). Although data compression techniques reduce storage requirements greatly, the storage and processing costs associated with high-resolution satellite data often make medium and low-resolution data preferable for analyses of extensive areas.
A second aspect of resolution is radiometric resolution, the measure of a sensor's ability to discriminate small differences in the magnitude of radiation within the ground area that corresponds to a single raster cell. The greater the bit depth (number of data bits per pixel) of the images that a sensor records, the higher its radiometric resolution. The AVHRR sensor, for example, stores 210 bits per pixel, as opposed to the 28 bits that older Landsat sensors recorded. Thus, although its spatial resolution is very coarse (~4 km), the Advanced Very High-Resolution Radiometer takes its name from its high radiometric resolution.

A third aspect is spectral resolution, the ability of a sensor to detect small differences in wavelength. For example, panchromatic sensors record energy across the entire visible band - a relatively broad range of wavelengths. An object that reflects a lot of energy in the green portion of the visible band may be indistinguishable in a panchromatic image from an object that reflects the same amount of energy in the red portion, for instance. A sensing system with higher spectral resolution would make it easier to tell the two objects apart. “Hyperspectral” sensors can discern up to 256 narrow spectral bands over a continuous spectral range across the infrared, visible, and ultraviolet wavelengths.

Finally, there is temporal resolution, the frequency at which a given site is sensed. This may be expressed as "revisit time" or "repeat cycle." High temporal resolution is valued in applications like monitoring wildland fires and floods, and is an appealing advantage of a new generation of micro- and nano-satellite sensors, as well as unmanned aerial systems (UAS).
7. Site Visit to USGS Earthshots
Try This!
Landsat is the earliest and most enduring mission to produce Earth imagery for civilian applications. The U.S. National Aeronautics and Space Administration (NASA) and Department of Interior worked together to launch the first Earth Resource Technology Satellite (ERTS-1) in 1972. When the second satellite lifted off in 1975, NASA renamed the program Landsat. Landsat sensors have been producing medium-resolution imagery more or less continuously since then. We'll look into the most recent sensor system - Landsat 8 - later in this chapter. Meanwhile, let's see what we can learn from Landsat data and applications about the nature of remotely sensing image data.
This activity involves a site visit to Earthshots, a website created by the USGS to publicize the many contributions of remote sensing to environmental science. We've been sending students to Earthshots for years. However, USGS has recently revised the site to make it more layman-friendly. The new site is less useful, but fortunately the older pages were archived and are still available. So, after taking you briefly to the new Earthshots homepage, we'll direct you to the older pages that are more instructive.
1. To begin, point your browser to the newer Earthshots site. Go ahead and look around the site. Note the information found by following the About Earthshots button.

2. Next, go to the archived older version of the USGS Earthshots site.

3. View images produced from Landsat data. Follow the link to the Garden City, Kansas example. You'll be presented with an image created from Landsat data of Garden City, Kansas in 1972. By clicking the date link below the lower left corner of the image, you can compare images produced from Landsat data collected in 1972 and 1988.

4. Zoom in to a portion of the image. Four yellow corner ticks outline a portion of the image that is linked to a magnified view. Click within the ticks to view the magnified image.

5. View a photograph taken on the ground. Click on one of the little camera icons arranged one above the other in the western quarter of the image. A photograph taken on the ground will appear.

6. Explore articles linked to the example. Find answers to the following questions in the related articles entitled What the colors mean, How images represent Landsat data, MSS and TM bands, and Beyond looking at pictures.
- What is the spectral sensitivity of the Landsat MSS sensor used to captured the image data?
- Which wavelength bands are represented in the image?
- What does the red color signify?
- How was "contrast stretching" used to enhance the images?
- What is the spatial resolution of the MSS data from which the images were produced?

8. Passive Sensing at Visible and Infrared Wavelengths
Over the next four pages, we'll survey some of the sensing systems used to capture Earth imagery in the visible, near-infrared, and thermal infrared bands. A common characteristic of these systems is the passive way in which they measure electromagnetic energy reflected or emitted from Earth's surface. One weakness of the desktop scanner analogy is that the sensors discussed here don't illuminate the objects they scan. We begin by considering aircraft and other platforms used for high-resolution sensing of relatively small areas from relatively low altitudes. Then we consider the origins, current status, and the outlook for remote sensing from space. The section concludes with a site visit to a leading commercial imagery provider.
9. Aerial Imaging
In contrast to remote sensing satellites that orbit the earth at altitudes of hundreds of kilometers (often upwards of 50 miles), “aerial imaging” refers to remote sensing from aircraft that typically fly 20,000 feet “above mean terrain.” For applications in which maximum spatial and temporal resolutions are needed, aerial imaging still has its advantages.
Aircraft platforms range from small, slow, and low flying, to twin-engine turboprops (like the one shown below) even and small jets capable of flying at altitudes up to 35,000 feet.

In chapter 6, you learned (or perhaps you already knew) that the U.S. National Agricultural Imagery Program (NAIP) flies aerial imaging missions over much of the lower 48 states every year. Just as digital cameras have replaced film cameras for most of us on the ground, digital sensors have all but replaced cameras for aerial surveys like NAIP. One reason for this transition is improved spatial resolution. Whereas the spatial resolution of a high-resolution aerial photograph was about 30-50 cm, the resolution that can be achieved by modern digital aerial imaging systems is great as 3 cm GSD. Another reason is that digital instruments can simultaneously capture imagery in multiple bands of the electromagnetic spectrum.
One example of a digital camera that’s widely used for mapping is the Leica DMC series, which provide four-band imagery at ground resolutions from 3cm to 80 cm GSD. Sophisticated instruments like this can cost more than the aircraft that carry them.
Unmanned Aerial Vehicles
UAVs (or, more generally, Unmanned Aerial Systems - UAS) are tantalizing platforms for aerial imaging. Unlike aircraft, UAVs are affordable to end users. So, one benefit to users is autonomy - the ability to collect one’s own imagery on one’s own timetable. And even equipped with relatively inexpensive imaging instruments, UAVs can deliver high-quality imagery because they fly at such low altitudes (typically around 400 feet). An important disadvantage is that the use of UAVs for civilian mapping is restricted in the U.S. by the Federal Aviation Administration. Still, interest in UAVs for mapping is so keen that xyHt magazine dubbed 2014 the “Year of the UAS.” Penn State’s Online Geospatial Education program offers an elective course called “Geospatial Applications of Unmanned Aerial Systems."

10. Early Space Imaging Systems
Christopher Lavers published an informative short history of the "Origins of High Resolution Civilian Satellite Imaging" in Directions Magazine in 2013. He points out that remote sensing from space began in the 1960s as a surveillance technology, in the wake of the Soviet Union's disruptive launch of Sputnik I in 1958.
Corona
In 1959, the U.S. launched its first Corona satellite (then called Discoverer 4), one in a series of launches that performed secret photographic reconnaissance until 1972 from an altitude of about 160 km. Photographic film exposed in space was returned to Earth in reentry capsules that were subsequently retrieved by aircraft and returned to the U.S. for processing and analysis. Not declassified until 1992, the panchromatic image below reveals an Israeli nuclear reactor.

KVR-1000 / SPIN-2
High-resolution panchromatic image data first became available to civilians in 1994, when the Russian space agency SOVINFORMSPUTNIK began selling surveillance photos to raise cash in the aftermath of the breakup of the Soviet Union. The photos were taken with a camera system called KVR 1000 which was mounted in unmanned space capsules like the Corona satellites. After orbiting Earth at altitudes of 220 km for about 40 days, the capsules separate from the Cosmos rockets that propelled them into space, and spiral slowly back to Earth. After the capsules parachute to the surface, ground personnel retrieve the cameras and transport them to Moscow, where the film is developed. Photographs were then shipped to the U.S., where they were scanned and processed by Kodak Corporation. The final product was two-meter resolution, georeferenced, and orthorectified digital data called SPIN-2.

IKONOS
Also in 1994, a new company called Space Imaging, Inc. was chartered in the U.S. Recognizing that high-resolution images were then available commercially from competing foreign sources, the U.S. government authorized private firms under its jurisdiction to produce and market remotely sensed data at spatial resolutions as high as one meter. By 1999, after a failed first attempt, Space Imaging successfully launched its Ikonos I satellite into an orbital path that circles the Earth 640 km above the surface, from pole to pole, crossing the equator at the same time of day, every day. Such an orbit is called a sun synchronous polar orbit, in contrast with the geosynchronous orbits of communications and some weather satellites that remain over the same point on the Earth's surface at all times.

Ikonos' panchromatic sensor records reflectances in the visible band at a spatial resolution of one meter, and a bit depth of eleven bits per pixel. The expanded bit depth enables the sensor to record reflectances more precisely, and allows technicians to filter out atmospheric haze more effectively than is possible with 8-bit imagery.
A competing firm called ORBIMAGE acquired Space Imaging in early 2006, after ORBIMAGE secured a half-billion dollar contract with the National Geospatial-Intelligence Agency. The merged companies were called GeoEye, Inc. In early 2013, DigitalGlobe corporation acquired GeoEye. Ikonos is still in operation, and Ikonos data are available from DigitalGlobe.
DMSP
The U.S. Air Force initiated its Defense Meteorology Satellite Program (DMSP) in the mid-1960s. By 2001, they had launched fifteen DMSP satellites. The satellites follow polar orbits at altitudes of about 830 km, circling the Earth every 101 minutes.
The program's original goal was to provide imagery that would aid high-altitude navigation by Air Force pilots. DMSP satellites carry several sensors, one of which is sensitive to a band of wavelengths encompassing the visible and near-infrared wavelengths (0.40-1.10 µm). The spatial resolution of this panchromatic sensor is low (2.7 km), but its radiometric resolution is high enough to record moonlight reflected from cloud tops at night. During cloudless new moons, the sensor is able to detect lights emitted by cities and towns. Image analysts have successfully correlated patterns of night lights with population density estimates produced by the U.S. Census Bureau, enabling analysts to use DMSP imagery (in combination with other data layers, such as transportation networks) to monitor changes in global population distribution.

11. Multispectral Imaging from Space
The preceding page on early space imaging systems focused on panchromatic photographs and images. However, a key takeaway from this chapter is that multispectral remote sensing enables analysts to differentiate objects that are hard to tell apart in the visible band. This page considers characteristics and applications of some of the most important multispectral sensing systems operated by government agencies as well as private commercial firms.
Government Systems
Some of the earliest space imaging platforms included multispectral sensors. One of those, which you explored a little earlier, is the Landsat program. Other U.S. government programs we'll consider briefly are AVHRR and MODIS.
Landsat MSS, TM and ETM+
Landsat satellites 1-5 (1972-1992) carried a four-band Multispectral Scanner (MMS) whose spectral sensitivity included visible green, visible red, and two near IR wavelengths. A new sensing system called Thematic Mapper (TM) was added to Landsat 4 in 1982. TM featured higher spatial resolution than MSS (30 meters in most channels) and expanded spectral sensitivity (seven bands, including visible blue, visible green, visible red, near-infrared, two mid-infrared, and thermal infrared wavelengths). An Enhanced Thematic Mapper Plus (ETM+) sensor, which included an eighth (panchromatic) band with a spatial resolution of 15 meters, was onboard Landsat 7 when it successfully launched in 1999.
Characteristics of the Landsat 5 TM and Landsat 7 ETM+ - including orbital height, spatial resolution, pass over time, spectral coverage, and data access and uses - are documented at Wikipedia's Remote Sensing Satellite and Data Overview page.
Try This!
Visit the USGS' LandsatLook Viewer, which displays natural color images for all Landsat 1-8 images in the USGS archive.
Landsat 8 - OLI and TIRS
NASA's Landsat Data Continuity Mission (LDCM) launched the Landsat 8 satellite in February 2013. The satellite payload includes two sensors, the Operational Land Imager (OLI) and the Thermal Infrared Sensor (TIRS).
The spatial resolution of the Landsat 8 data is comparable to that of the Landsat 7 data. In regard to spectral resolution, six of the Landsat 8 bands have spectral sensitivities comparable to Landsat 7, but they have been refined somewhat. For example, the NIR band has been fine-tuned to decrease the effects of atmospheric absorption. The spectral sensitivities of Landsat 7 and 8 are compared in the figure below.

Landsat 7 is still collecting data. Landsat 8 orbits at the same altitude as Landsat 7. Both satellites complete an orbit in 99 minutes, and complete close to 14 orbits per day. This results in every point on Earth being crossed every 16 days. But, because the orbits of the two satellites are offset, it results in repeat coverage every 8 days. Approximately 1000 images per day are collected by Landsat 7 and Landsat 8 combined. That is almost double the images collected when Landsat 5 and Landsat 7 were operating concurrently.
While characteristics of Landsat 8 are documented at and is documented at Wikipedia's Remote Sensing Satellite and Data Overview page, the following table outlines scientific applications associated with each sensor band.
| Spectral Bands | Spatial Resolution | Phenomena Revealed/Use |
|---|---|---|
| 0.43 - 0.45 μm (Band 1 - visible deep-blue) |
30 m | Coastal/aerosol; increased coastal zone observations |
| 0.45 - 0.51 μm (Band 2 - visible blue) |
30 m | Bathymetric mapping; distinguishes soil from vegetation; deciduous from coniferous vegetation |
| 0.53 - 0.59 μm (Band 3 - visible green) |
30 m | Emphasizes peak vegetation, which is useful for assessing plant vigor |
| 0.64 - 0.67 μm (Band 4 - visible red) |
30 m | Emphasizes vegetation on slopes |
| 0.85 - 0.88 μm (Band 5 - near IR) |
30 m | Emphasizes vegetation boundary between land and water, and landforms |
| 1.57 - 1.65 μm (Band 6 - SWIR 1) |
30 m | Used in detecting plant drought stress and delineating burnt areas and fire-affected vegetation, and is also sensitive to the thermal radiation emitted by intense fires; can be used to detect active fires, especially during nighttime when the background interference from SWIR in reflected sunlight is absent |
| 2.11 – 2.29 μm (Band 7 - SWIR-1) |
30 m | Used in detecting drought stress, burnt and fire-affected areas, and can be used to detect active fires, especially at nighttime |
| 0.50 – 0.68 μm (Band 8 - panchromatic) |
15 m | Useful in ‘sharpening’ multispectral images |
| 1.36 – 1.38 μm (Band 9 - cirrus) |
30 m | Useful in detecting cirrus clouds |
| 10.60 - 11.19 μm (Band 10 - Thermal IR 1) |
100 m | Useful for mapping thermal differences in water currents, monitoring fires, and other night studies, and estimating soil moisture |
| 11.50 - 12.51 μm (Band 11 - Thermal IR 2) |
100 m | Same as band 10 |
AVHRR
Another longstanding U.S. remote sensing program is AVHRR. The acronym stands for "Advanced Very High-Resolution Radiometer." AVHRR sensors have been onboard sixteen satellites maintained by the National Oceanic and Atmospheric Administration (NOAA) since 1979. The data the sensors produce are widely used for large-area studies of vegetation, soil moisture, snow cover, fire susceptibility, and floods, among other things.
AVHRR sensors measure electromagnetic energy within five spectral bands, including visible red, near infrared, and three thermal infrared. The visible red and near-infrared bands are particularly useful for large-area vegetation monitoring. The Normalized Difference Vegetation Index (NDVI), a widely used measure of photosynthetic activity that is calculated from reflectance values in these two bands, is discussed later.
MODIS
First launched in 1999, NASA's 36-band Moderate Resolution Imaging Spectroradiometer (MODIS) sensor has superseded AVHRR for many applications, including NDVI calculations for vegetation mapping.
Characteristics of the AVHRR and MODIS sensors are documented at Wikipedia's Remote Sensing Satellite and Data Overview page.

Commercial Systems
Christopher Lavers' 2013 article Origins of High-Resolution Civilian Satellite Imaging - Part 2 profiles several commercial systems, including SPOT, IKONOS, OrbView, and GeoEye. Characteristics of these and other contemporary sensing systems are documented at Wikipedia's Remote Sensing Satellite and Data Overview page. Not included in that page is DigitalGlobe's WorldView-3 sensor, which launched in August 2014. WorldView-3 provides panchromatic imaging at 31 cm GSD and 1.24 m multispectral. Datasheets for WorldView-3 and other DigitalGlobe sensors are available at its Satellite Information page. Coming up next in this chapter is a site visit to DigitalGlobe.
Next Generation Satellite Imaging
Also missing from the Wikipedia summary table is the new generation of micro- and nano-satellite space imaging providers like Skybox and Planet Labs. A 2014 article in IEEE Spectrum entitled "9 Earth-Imaging Startups to Watch" suggests that while "there's at most two dozen nonmilitary satellites doing Earth imaging ... Five years from now [that is, in 2020] there might be 200 or more."


12. Site Visit to DigitalGlobe
Try This!
DigitalGlobe began as WorldView Imaging Corporation, one of several companies founded inanticipation of the 1992 Land Remote Sensing Policy Act, which created thecommercialsatellite imaging business in the U.S. Another startup was ORBIMAGE, which was renamed GeoEye after acquiring Space Imaging Corporation. DigitalGlobe became theworld’s largest commercial provider of earth imaging products after it acquired GeoEye in 2013.This site visit is meant to acquaint you with with the kinds of sensors, data products and services a provider like DigitalGlobe offers.
The instructions below are based on the October 2015 version of the website. Please bear in mind that websites change without notice.
1. First, go to DigitalGlobe’s home page and scroll to the bottom, where you’ll find a list of CONTENT.
Follow links in that list to explore DigitalGlobe’s various products and services, including Imagery, Elevation, and Human Landscape.
2. In the list of CONTENT, follow the Imagery Suitelink and explore DigitalGlobe’s imagery products, including Basic Imagery, Standard Imagery, Precision Aerial, and New Collection Request. The latter allows satellite tasking requests to be made.
4. Near the bottom of each Imagery product page you should find a link to a Datasheet. Click the link to view the datasheet. (It will open in a new window or tab.)

5. Study the data sheets with a few questions in mind: What’s the difference between “Basic” and “Standard” imagery? Which sensing systemscontribute to each imagery product? Which image bands are available? What information about spatial (pixel) and radiometric resolution are provided?

6. Next, let’s see whatimagery products are available for your area of interest.Go back to the main page and scroll all the way to the bottom again and follow the Quick Link to Search Imagery.
Following the Search Imagery link will open the ImageFinder tool. As of this writing, it looked like the image below.
7. Enter a place name in the Go To: field to search the gazetteer. I was interested in chose Perth, Australia, but I just typed Perth into the field.

8. Next, click the green “Go to this location” arrow head. That will open the ImageFinder Gazetteer window, showing in my case a list of locations in the world named Perth.

8. In the Gazetteer list I clicked on the first entry, for Perth, Australia. The Gazetteer window closes and the map zooms to the vicinity of Perth, Australia.

9. Next, in the Search Filter box to the right of the map, click Search to query for imagery tracks that intersect the map bounding box.
Wait for it... eventually you should get a new Catalog window that lists the imagery available for your selected area. Here’s what I got:

In the Catalog list above, notice the variety of spacecraft (sensor “vehicles”), bands, dates, andmaximum spatial resolution (Ground Sample Distance). Why do you suppose a maximum is given, rather than a single GSD value?
10. Clicking on an entry in the Catalog list turns it yellow and also highlights the area on the map covered by the selected image.

11. Finally, here’s what I received after clicking to View the most recent image listed.
You can zoom in or out by choosing from the Image Resize pick list.

Maybe you’re wondering how much you’d have to pay to acquire that scene? You won’t find prices on DigitalGlobe’s web site. However, we were able to find a bootleg copy of DigitalGlobe’s price book with a simple web search. Or of course you can contact DigitalGlobe or an authorized reseller.
That’s it for our site visit. Hope you enjoyed it.

13. Multispectral Image Processing
Obviously, one of the main advantages of digital data is that they can be processed using digital computers. Over the next few pages, we focus on digital image processing techniques used to correct, enhance, and classify remotely sensed image data.
14. Image Correction
As suggested earlier, scanning the Earth's surface from space is like scanning a paper document with a desktop scanner, only a lot more complicated. Raw remotely sensed image data are full of geometric and radiometric flaws caused by the curved shape of the Earth, the imperfectly transparent atmosphere, daily and seasonal variations in the amount of solar radiation received at the surface, and imperfections in scanning instruments, among other things. Understandably, most users of remotely sensed image data are not satisfied with the raw data transmitted from satellites to ground stations. Most prefer preprocessed data from which these flaws have been removed.
Geometric correction
You read in Chapter 6 that scale varies in unrectified aerial imagery due to the relief displacement caused by variations in terrain elevation. Relief displacement is one source of geometric distortion in digital image data, although it is less of a factor in satellite remote sensing than it is in aerial imaging because satellites fly at much higher altitudes than airplanes. Another source of geometric distortions is the Earth itself, whose curvature and eastward spinning motion are more evident from space than at lower altitudes.
The Earth rotates on its axis from west to east. At the same time, remote sensing satellites orbit the Earth from pole to pole. If you were to plot on a cylindrical projection the flight path that a polar-orbiting satellite traces over a 24-hour period, you would see a series of S-shaped waves. As a remote sensing satellite follows its orbital path over the spinning globe, each scan row begins at a position slightly west of the row that preceded it. In the raw scanned data, however, the first pixel in each row appears to be aligned with the other initial pixels. To properly georeference the pixels in a remotely sensed image, pixels must be shifted slightly to the west in each successive row. This is why processed scenes are shaped like skewed parallelograms when plotted in geographic or plane projections, as shown in the image below.

In addition to the systematic error caused by the Earth's rotation, random geometric distortions result from relief displacement, variations in the satellite altitude and attitude, instrument misbehaviors, and other anomalies. Random geometric errors may be corrected through a process known as rubber sheeting. As the name implies, rubber sheeting involves stretching and warping an image to georegister control points shown in the image to known control point locations on the ground. First, a pair of plane coordinate transformation equations is derived by analyzing the differences between control point locations in the image and on the ground. The equations enable image analysts to generate a rectified raster grid. Next, reflectance values in the original scanned grid are assigned to the cells in the rectified grid. Since the cells in the rectified grid don't align perfectly with the cells in the original grid, reflectance values in the rectified grid cells have to be interpolated from values in the original grid. This process is called resampling. Resampling is also used to increase or decrease the spatial resolution of an image so that its pixels can be georegistered with those of another image.
Radiometric correction
The reflectance at a given wavelength of an object measured by a remote sensing instrument varies in response to several factors, including the illumination of the object, its reflectivity, and the transmissivity of the atmosphere. Furthermore, the response of a given sensor may degrade over time. With these factors in mind, it should not be surprising that an object scanned at different times of the day or year will exhibit different radiometric characteristics. Such differences can be advantageous at times, but they can also pose problems for image analysts who want to mosaic adjoining images together or to detect meaningful changes in land use and land cover over time. To cope with such problems, analysts have developed numerous radiometric correction techniques, including Earth-sun distance corrections, sun elevation corrections, and corrections for atmospheric haze.
To compensate for the different amounts of illumination of scenes captured at different times of day, or at different latitudes or seasons, image analysts may divide values measured in one band by values in another band, or they may apply mathematical functions that normalize reflectance values. Such functions are determined by the distance between the Earth and the sun and the altitude of the sun above the horizon at a given location, time of day, and time of year. Analysts depend on metadata that include the location, date, and time at which a particular scene was captured.
Image analysts may also correct for the contrast-diminishing effects of atmospheric haze. Haze compensation resembles the differential correction technique used to improve the accuracy of GPS data in the sense that it involves measuring error (or, in this case, spurious reflectance) at a known location, then subtracting that error from another measurement. Analysts begin by measuring the reflectance of an object known to exhibit near-zero reflectance under non-hazy conditions, such as deep, clear water in the near-infrared band. Any reflectance values in those pixels can be attributed to the path radiance of atmospheric haze. Assuming that atmospheric conditions are uniform throughout the scene, the haze factor may be subtracted from all pixel reflectance values. Some new sensors allow "self calibration" by measuring atmospheric water and dust content directly.
The data sheets you viewed during your site visit to DigitalGlobe.com outlined different radiometric and geometric corrections applied to Basic and Standard imagery,
15. Image Enhancement
Correction techniques are routinely used to resolve geometric, radiometric, and other problems found in raw remotely sensed data. Another family of image processing techniques is used to make image data easier to interpret. These so-called image enhancement techniques include contrast stretching, edge enhancement, and deriving new data by calculating differences, ratios, or other quantities from reflectance values in two or more bands, among many others. This section considers briefly two common enhancement techniques: contrast stretching and derived data. Later you'll learn how vegetation indices derived from the visible red and near-infrared bands are used to monitor vegetation health at a global scale.
Contrast stretching
Consider the pair of images shown side by side in Figure 8.16.1. Although both were produced from the same Landsat MSS data, you will notice that the image on the left is considerably dimmer than the one on the right. The difference is a result of contrast stretching. MSS data have a precision of 8 bits; that is, reflectance values are encoded as 256 (28) intensity levels. As is often the case, reflectances in the near-infrared band of the scene partially shown below ranged from only 30 and 80 in the raw image data. This limited range results in an image that lacks contrast and, consequently, appears dim. The image on the right shows the effect of stretching the range of reflectance values in the near-infrared band from 30-80 to 0-255, and then similarly stretching the visible green and visible red bands. As you can see, the contrast-stretched image is brighter and clearer.

Derived data: NDVI
One advantage of multispectral data is the ability to derive new data by calculating differences, ratios, or other quantities from reflectance values in two or more wavelength bands. For instance, detecting stressed vegetation amongst healthy vegetation may be difficult in any one band, particularly if differences in terrain elevation or slope cause some parts of a scene to be illuminated differently than others. The ratio of reflectance values in the visible red band and the near-infrared band compensates for variations in scene illumination, however. Since the ratio of the two reflectance values is considerably lower for stressed vegetation regardless of illumination conditions, detection is easier and more reliable.
Besides simple ratios, remote sensing scientists have derived other mathematical formulae for deriving useful new data from multispectral imagery. One of the most widely used examples is the Normalized Difference Vegetation Index (NDVI). NDVI scores are calculated pixel-by-pixel using the following algorithm:
NDVI = (NIR - R) / (NIR + R)
R stands for the visible red band (MODIS and AVHRR channel 1), while NIR represents the near-infrared band (MODIS and AVHRR channel 2). The chlorophyll in green plants strongly absorbs radiation in the visible red band during photosynthesis. In contrast, leaf structures cause plants to strongly reflect radiation in the near-infrared band. NDVI scores range from -1.0 to 1.0. A pixel associated with low reflectance values in the visible band and high reflectance in the near-infrared band would produce an NDVI score near 1.0, indicating the presence of healthy vegetation. Conversely, the NDVI scores of pixels associated with high reflectance in the visible band and low reflectance in the near-infrared band approach -1.0, indicating clouds, snow, or water. NDVI scores near 0 indicate rock and non-vegetated soil.
Applications of the NDVI range from local to global. At the local scale, the Mondavi Vineyards in Napa Valley California can attest to the utility of NDVI data in monitoring plant health. In 1993, the vineyards suffered an infestation of phylloxera, a species of plant lice that attacks roots and is impervious to pesticides. The pest could only be overcome by removing infested vines and replacing them with more resistant root stock. The vineyard commissioned a consulting firm to acquire visible and near-infrared imagery during consecutive growing seasons using an airborne sensor. Once the data from the two seasons were georegistered, comparison of NDVI scores revealed areas in which vine canopy density had declined. NDVI change detection proved to be such a fruitful approach that the vineyards adopted it for routine use as part of their overall precision farming strategy (Colucci, 1998). Many more recent case studies abound.
The case study described on the following page outlines the image processing steps involved in producing a global NDVI data set.
16. Case Study: Processing a Global Land Dataset
Environmental scientists rely on global vegetation and land cover data to monitor drought conditions that may lead to famine and to calibrate global- and regional-scale climate models, among other uses. Land cover studies around the world vary greatly both temporally and spatially. The most detailed contemporary global land datasets we're aware of is GlobeLand30, which depicts ten land cover types at 30-meter resolution for Earth's entire land surface, for both 2000 and 2010. China's National Geomatics Center produced the datasets from over 20,000 Landsat and Chinese HJ-1 scenes and donated them to the United Nations in September 2014. Other global datasets include GlobCover, a 22-class, 300-meter resolution dataset created by the European Space Agency. They created GlobCover from imagery produced by the Envisat Medium Resolution Imaging Spectrometer (MERIS) from 2004-06, then again in 2009. The Global Land Cover Facility at the University of Maryland offers more recent if lower resolution MODIS land cover and vegetation annual mosaics for 2001-2017. Meanwhile, beginning in 2014, Esri collaborated with USGS to create a Global Ecological Land Units map that characterizes each 250-meter resolution "facet" of Earth's surface as a function of four input layers that drive ecological processes: bioclimate, landform, lithology, and land cover.
The following case study describes the production of one of the earliest global composite vegetation maps. While it is a historical example, it is an exceptionally well-documented one that illuminates an image processing workflow that remains relevant today.
The Advanced Very High-Resolution Radiometer (AVHRR) sensors aboard NOAA satellites scan the entire Earth daily at visible red, near-infrared, and thermal infrared wavelengths. In the late 1980s and early 1990s, several international agencies identified the need to compile a baseline, cloud-free, global NDVI data set in support of efforts to monitor global vegetation cover. For example, the United Nations mandated its Food and Agriculture Organization to perform a global forest inventory as part of its Forest Resources Assessment Project. Scientists participating in NASA's Earth Observing System program also needed a global AVHRR data set of uniform quality to calibrate computer models intended to monitor and predict global environmental change. In 1992, under contract with the USGS, and in cooperation with the International Geosphere Biosphere Programme, scientists at the EROS Data Center in Sioux Falls, South Dakota started work. Their goals were to create not only a single 10-day composite image, but also a 30-month time series of composites that would help Earth system scientists to understand seasonal changes in vegetation cover at a global scale.
From 1992 through 1996, a network of 30 ground receiving stations acquired and archived tens of thousands of scenes from an AVHRR sensor aboard one of NOAA's polar orbiting satellites. Individual scenes were stitched together into daily orbital passes like the ones illustrated below. Creating orbital passes allowed the project team to discard the redundant data in overlapping scenes acquired by different receiving stations.

Once the daily orbital scenes were stitched together, the project team set to work preparing cloud-free, 10-day composite data sets that included Normalized Difference Vegetation Index (NDVI) scores. The image processing steps involved included radiometric calibration, atmospheric correction, NDVI calculation, geometric correction, regional compositing, and projection of composited scenes. Each step is described briefly below.
Radiometric calibration
Radiometric calibration means defining the relationship between reflectance values recorded by a sensor from space and actual radiances measured with spectrometers on the ground. The accuracy of the AVHRR visible red and near-IR sensors degrade over time. Image analysts would not be able to produce useful time series of composite data sets unless reflectances were reliably calibrated. The project team relied on research that showed how AVHRR data acquired at different times could be normalized using a correction factor derived by analyzing reflectance values associated with homogeneous desert areas.
Atmospheric correction
Several atmospheric phenomena, including Rayleigh scatter, ozone, water vapor, and aerosols were known to affect reflectances measured by sensors like AVHRR. Research yielded corrections to compensate for some of these.
One proven correction was for Rayleigh scatter. Named for an English physicist who worked in the early 20th century, Rayleigh scatter is the phenomenon that accounts for the fact that the sky appears blue. Short wavelengths of incoming solar radiation tend to be diffused by tiny particles in the atmosphere. Since blue wavelengths are the shortest in the visible band, they tend to be scattered more than green, red, and other colors of light. Rayleigh scatter is also the primary cause of atmospheric haze.
Because the AVHRR sensor scans such a wide swath, image analysts couldn't be satisfied with applying a constant haze compensation factor throughout entire scenes. To scan its 2400-km wide swath, the AVHRR sensor sweeps a scan head through an arc of 110°. Consequently, the viewing angle between the scan head and the Earth's surface varies from 0° in the middle of the swath to about 55° at the edges. Obviously, the lengths of the paths traveled by reflected radiation toward the sensor vary considerably depending on the viewing angle. Project scientists had to take this into account when compensating for atmospheric haze. The further a pixel was located from the center of a swath, the greater its path length, and the more haze needed to be compensated for. While they were at it, image analysts also factored in terrain elevation, since that, too, affects path length. ETOPO5, the most detailed global digital elevation model available at the time, was used to calculate path lengths adjusted for elevation. (You learned about the more detailed ETOPO1 in Chapter 7.)
NDVI calculation
The Normalized Difference Vegetation Index (NDVI) is the difference of near-IR and visible red reflectance values normalized over the sum of the two values. The result, calculated for every pixel in every daily orbital pass, is a value between -1.0 and 1.0, where 1.0 represents maximum photosynthetic activity, and thus maximum density and vigor of green vegetation.
Geometric correction and projection
As you can see in the stitched orbital passes illustrated above, the wide range of view angles produced by the AVHRR sensor results in a great deal of geometric distortion. Relief displacement makes matters worse, distorting images even more towards the edges of each swath. The project team performed both orthorectification and rubber sheeting to rectify the data. The ETOPO5 global digital elevation model was again used to calculate corrections for scale distortions caused by relief displacement. To correct for distortions caused by the wide range of sensor view angles, analysts identified well-defined features like coastlines, lakeshores, and rivers in the imagery that could be matched to known locations on the ground. They derived coordinate transformation equations by analyzing differences between positions of control points in the imagery and known locations on the ground. The accuracy of control locations in the rectified imagery was shown to be no worse than 1,000 meters from actual locations. Equally important, the georegistration error between rectified daily orbital passes was shown to be less than one pixel.
After the daily orbital passes were rectified, they were transformed into a map projection called Goode's Homolosine. This is an equal-area projection that minimizes shape distortion of land masses by interrupting the graticule over the oceans. The project team selected Goode's projection in part because they knew that equivalence of area would be a useful quality for spatial analysis. More importantly, the interrupted projection allowed the team to process the data set as twelve separate regions that could be spliced back together later. Figure 8.17.2 shows the orbital passes for June 24, 1992, projected together in a single global image based on Goode's projection.

Compositing
Once the daily orbital passes for a ten-day period were rectified, every one-kilometer square pixel could be associated with corresponding pixels at the same location in other orbital passes. At this stage, with the orbital passes assembled into twelve regions derived from the interrupted Goode's projection, image analysts identified the highest NDVI value for each pixel in a given ten-day period. They then produced ten-day composite regions by combining all the maximum-value pixels into a single regional data set. This procedure minimized the chances that cloud-contaminated pixels would be included in the final composite data set. Finally, the composite regions were assembled into a single data set, illustrated below. This same procedure has been repeated to create 93 ten-day composites from April 1-10, 1992 to May 21-30, 1996.

17. Image Classification
Back in Chapter 3, we considered the classification of thematic data for choropleth maps. Remember? We approached data classification as a kind of generalization technique, and made the claim that "generalization helps make sense of complex data." The same is true in the context of remotely sensed image data.
A key trend in image classification is the emergence of object-based alternatives to traditional pixel-based techniques. A Penn State lecturer has observed, "For much of the past four decades, approaches to the automated classification of images have focused almost solely on the spectral properties of pixels" (O'Neil-Dunne, 2011). Pixel-based approaches made sense initially, O'Neil-Dunne points out, since "processing capabilities were limited and pixels in the early satellite images were relatively large and contained a considerable amount of spectral information." In recent years, however, pixel-based approaches have begun to be overtaken by object-based image analysis (OBIA) for high-resolution multispectral imagery, especially when fused with lidar data. OBIA is beyond the scope of this chapter, but you can study it in depth in the open-access Penn State courseware GEOG 883: Remote Sensing Image Analysis and Applications.
Pixel-based classification techniques are commonly used in land use and land cover mapping from imagery. These are explained below and in the following case study.
The term land cover refers to the kinds of vegetation that blanket the Earth's surface, or the kinds of materials that form the surface where vegetation is absent. Land use, by contrast, refers to the functional roles that the land plays in human economic activities (Campbell, 1983).
Both land use and land cover are specified in terms of generalized categories. For instance, an early classification system adopted by a World Land Use Commission in 1949 consisted of nine primary categories, including settlements and associated non-agricultural lands, horticulture, tree and other perennial crops, cropland, improved permanent pasture, unimproved grazing land, woodlands, swamps and marshes, and unproductive land. Prior to the era of digital image processing, specially trained personnel drew land use maps by visually interpreting the shape, size, pattern, tone, texture, and shadows cast by features shown in aerial photographs. As you might imagine, this was an expensive, time-consuming process. It's not surprising, then, that the Commission appointed in 1949 failed in its attempt to produce a detailed global land use map.
Part of the appeal of digital image processing is the potential to automate land use and land cover mapping. To realize this potential, image analysts have developed a family of image classification techniques that automatically sort pixels with similar multispectral reflectance values into clusters that, ideally, correspond to functional land use and land cover categories. Two general types of pixel-based image classification techniques have been developed: supervised and unsupervised techniques.
Supervised classification
Human image analysts play crucial roles in both supervised and unsupervised image classification procedures. In supervised classification, the analyst's role is to specify in advance the multispectral reflectance or (in the case of the thermal infrared band) emittance values typical of each land use or land cover class.

For instance, to perform a supervised classification of the Landsat Thematic Mapper (TM) data shown above into two land cover categories, Vegetation and Other, you would first delineate several training fields that are representative of each land cover class. The illustration below shows two training fields for each class; however, to achieve the most reliable classification possible, you would define as many as 100 or more training fields per class.

The training fields you defined consist of clusters of pixels with similar reflectance or emittance values. If you did a good job in supervising the training stage of the classification, each cluster would represent the range of spectral characteristics exhibited by its corresponding land cover class. Once the clusters are defined, you would apply a classification algorithm to sort the remaining pixels in the scene into the class with the most similar spectral characteristics. One of the most commonly used algorithms computes the statistical probability that each pixel belongs to each class. Pixels are then assigned to the class associated with the highest probability. Algorithms of this kind are known as maximum likelihood classifiers. The result is an image like the one shown below, in which every pixel has been assigned to one of two land cover classes.

Unsupervised classification
The image analyst plays a different role in unsupervised classification. They do not define training fields for each land cover class in advance. Instead, they rely on one of a family of statistical clustering algorithms to sort pixels into distinct spectral classes. Analysts may or may not even specify the number of classes in advance. Their responsibility is to determine the correspondences between the spectral classes that the algorithm defines and the functional land use and land cover categories established by agencies like the U.S. Geological Survey. The example that follows outlines how unsupervised classification contributes to the creation of a high-resolution national land cover data set.

The following case study contrasts unsupervised and supervised classification techniques used to create the U.S. National Land Cover Database.
18. Case Study: Image Classification for the National Land Cover Dataset
The USGS has used remotely sensed imagery to map land use and land cover since the 1970s. Analysts compiled the first Land Use and Land Cover dataset (LULC) by manual interpretation of aerial photographs acquired in the 1970s and 80s. The successor to LULC was the National Land Cover Dataset (NLCD), which USGS created from Landsat imagery in 1992, 2001, 2006, and 2011 at a spatial resolution of 30 meters. The following case study outlines the evolving workflow used to produce the NLCD, including a change in image classification approaches between the 1992 NLCD and later versions.
Preprocessing
The primary source data used to create NLCD 92 were the visible red, near-infrared, mid-infrared, and thermal infrared bands of cloud-free, leaf-off Landsat TM scenes acquired in 1992. In comparison, source data used for NLCD 2001 and later versions were more diverse. NLCD 2001 sources included "18 or more layers" of "multi-season Landsat 5 and Landsat 7 imagery ... and Digital Elevation Model derivatives" (Homer and others, 2007; USGS 2014). In 1992 as well as subsequent versions, selected scenes were geometrically and radiometrically corrected, then combined into sub-regional mosaics. Mosaics were then projected to the same Albers Conic Equal Area projection based upon the NAD83 horizontal datum, and then were resampled to 30-meter grid cells.
Image classification
From the outset, the LULC and NLCD datasets have used variations on the Anderson Land Use/Land Cover Classification system. The number and definitions of land use and land cover categories have evolved over the years since their original 1976 publication.
For NLCD 92, analysts applied an unsupervised classification algorithm to the preprocessed mosaics to generate 100 spectrally distinct pixel clusters. Using aerial photographs and other references, they then assigned each cluster to one of the classes in a modified version of the Anderson classification scheme. Considerable interpretation was required since not all functional classes have unique spectral response patterns.
From NLCD 2001 on, the USGS project team used "decision tree" (DT), "a supervised classification method that relies on large amounts of training data, which was initially collected from a variety of sources including high-resolution orthophotography, local datasets, field-collected points, and Forest Inventory Analysis data" (Homer and others, 2007). The training data were used to map all classes except the four urban classes, which were derived from an imperviousness data layer. A series of DT iterations was followed by localized modeling and hand editing.

For more information about the National Land Cover Datasets, visit the Multi-Resolution Land Characteristics Consortium
Accuracy Assessment
As you'd expect, the classification accuracy of NLCD data products has improved over the years.
The USGS hired private sector vendors to assess the classification accuracy of the NLCD 92 by checking randomly sampled pixels against manually interpreted aerial photographs. Results indicated that the likelihood that a given pixel was classified correctly was only 38 to 62 percent. USGS therefore encouraged NLCD 92 users to aggregate the data into 3 x 3 or 5 x 5-pixel blocks (in other words, to decrease spatial resolution from 30 meters to 90 or 150 meters), or to aggregate the (then) 21 Level II Anderson classes into the nine Level I classes.
A similar assessment of NLCD 2006 demonstrated that accuracy had indeed improved. Wickham and others (2013) found that overall accuracies for the NLCD 2001 and 2006 Level II Anderson class were 79% and 78%, respectively.
If that still doesn't seem very good, you'll appreciate why image processing scientists and software engineers are so motivated to perfect object-based image analysis techniques that promise greater accuracies. Even in the current era of high-resolution satellite imaging and sophisticated image processing techniques, there is still no cheap and easy way to produce detailed, accurate geographic data.
19. Unsupervised Classification by Hand
Try This!
This activity guides you through a simulated pixel-based unsupervised classification of remotely sensed image data to create a land cover map. Our goal is for you to gain a hands-on appreciation of automated image classification technique. Begin by viewing and printing the Image Classification Activity PDF file.
1. Plot the reflectance values.
The two grids on the top of the second page of the PDF file represent reflectance values in the visible red and near infrared wavelength bands measured by a remote sensing instrument for a parcel of land. Using the graph (like the one below) on the first page of the PDF file you printed, plot the reflectance values for each pixel and write the number of each pixel (1 to 36) next to its location in the graph. Pixel 1 has been plotted for you (Visible Red band = 22, Near Infrared band = 6).

- After you have completed filling in the graph, you can check your progress by following this link to a completed graph.
2. Identify four land cover classes.
Looking at the completed plot from step one, identify and circle four clusters (classes) of pixels. Label these four classes A, B, C, and D.
- After you have circled the four clusters of pixels in the graph, you can check your progress by following this link to view the identified clusters.
- Note: You may have labeled the clusters differently, but the four clusters should contain the same points, more or less, as the example.
3. Complete the land cover map grid.
Using the clusters you identified in the previous step, fill in the land cover map grid with the letter that represents the land use class in which each pixel belongs. The result is a classified image.

- If you would like to check your land cover map, you can follow this link to view a completed land cover map.
- Note: If you labeled the clusters in step two differently than the example, your land cover map may look different, but the patterns should look similar.
4. Complete a legend that explains the association.
Using the spectral response data provided on the second page of the PDF file, associate each of the four classes with a land use class.

- You can check your results by following this link to view a completed legend.
- Note: Depending on how you labeled your clusters, your legend may differ from the example legend; however, when you apply your legend to your Land Cover Map, the land use classes on your map should match the example map.
You have now completed the unsupervised classification activity in which you used remotely sensed image data to create a land cover map.

20. Active Remote Sensing Systems
The remote sensing systems you've studied so far are sensitive to the visible, near-infrared, and thermal infrared bands of the electromagnetic spectrum, wavelengths at which the magnitude of solar radiation is greatest. Quickbird, WorldView, Landsat and MODIS are all passive sensors that measure only radiation emitted by the Sun and reflected or emitted by the Earth.
Although we used the common desktop document scanner as an analogy for remote sensing instruments throughout this chapter, the analogy is actually more apt for active sensors. That's because desktop scanners must actively illuminate the object to be scanned. Similarly, active airborne and satellite-based sensors beam particular wavelengths of electromagnetic energy toward Earth's surface, and then measure the time and intensity of the pulses' returns. Over the next couple of pages, we'll consider two kinds of active sensors: imaging radar and lidar.

There are two main shortcomings to passive sensing of the visible and infrared bands. First, reflected visible and near-infrared radiation can only be measured during daylight hours. Second, clouds interfere with both incoming and outgoing radiation at these wavelengths. Though Lidar can be flown at night, it can't penetrate cloud cover.
Longwave radiation, or microwaves, are made up of wavelengths between about one millimeter and one meter. Microwaves can penetrate clouds, but the Sun and Earth emit so little longwave radiation that it can't be measured easily at altitude. Active imaging radar systems solve this problem. Active sensors like those aboard the European Space Agency's ERS and Envisat, India's RISAT, and Canada's Radarsat, among others, transmit pulses of longwave radiation, then measure the intensity and travel time of those pulses after they are reflected back to space from the Earth's surface. Microwave sensing is unaffected by cloud cover, and can operate day or night. Both image data and elevation data can be produced by microwave sensing, as you'll see in the following page.
21. Imaging Radar
One example of active remote sensing that everyone has heard of is radar, which stands for RAdio Detection And Ranging. Radar was developed as an air defense system during World War II and is now the primary remote sensing system air traffic controllers use to track the 40,000 daily aircraft takeoffs and landings in the U.S. Radar antennas alternately transmit and receive pulses of microwave energy. Since both the magnitude of energy transmitted and its velocity (the speed of light) are known, radar systems are able to record either the intensity or the round-trip distance traveled of pulses reflected back to the sensor. Chapter 7 mentioned the Shuttle Radar Topography Mission (SRTM) in the context of global elevation data. SRTM and other satellite altimeters measure the distance traveled by microwave pulses transmitted from the space shuttle Endeavor. Imaging radars, in contrast, measure pulse intensity.
In addition to its indispensable role in navigation, radar is also an important source of raster image data about the Earth's surface. Radar images look the way they do because of the different ways that objects reflect microwave energy. In general, rough-textured objects reflect more energy back to the sensor than smooth objects. Smooth objects, such as water bodies, are highly reflective, but unless they are perpendicular to the direction of the incoming pulse, the reflected energy all bounces off at an angle and never returns to the sensor. Rough surfaces, such as vegetated agricultural fields, tend to scatter the pulse in many directions, increasing the chance that some back scatter will return to the sensor.

The imaging radar aboard the European Resource Satellite (ERS-1) produced the data used to create the historical image shown above. The smooth surface of the flooded Mississippi River deflected the radio signal away from the sensor, while the surrounding rougher-textured land cover reflected larger portions of the radar pulse. The lighter an object appears in the image, the more energy it reflected. Imaging radar can be used to monitor flood extents day or night, regardless of weather conditions. Passive instruments that are sensitive only to visible and near-infrared wavelengths are useless as long as cloud-covered skies prevail.
22. Lidar
Lidar (LIght Detection And Ranging) also came up in Chapter 7, in the context of elevation data. But lidar is about much more than elevation. Along with GPS, it is one of the technologies that has truly revolutionized mapping.
So important has lidar become that Penn State has developed an entire course on it—Geography 481: Topographic Mapping with Lidar. The course is part of our Open Educational Resources Initiative, so you're free to browse its in-depth treatments of lidar system characteristics, data collection and processing techniques, and applications in topographic mapping, forestry, corridor mapping, and 3-D building modeling.
In this text, we'll emphasize just a few key points.
First, lidar is an active remote sensing technology. Like radar, lidar emits pulses of electromagnetic energy and measures the time and intensity of "returns" reflected from Earth's surface and objects on and above it. Unlike radar, lidar uses laser light. The wavelength chosen for most airborne topographic mapping lasers is 1064 nanometers, in the near-infrared band of the spectrum.
The product of a lidar scan is a 3-D cloud of mass point data. The density of points on the ground varies according to the mapping mission and platform from one to a few to hundreds of points per square meter, with corresponding accuracies of 10-15 cm to 1 cm or better. Crucial to data quality is the integration of GPS with inertial navigation systems—together called "direct georeferencing"—which enables precise positioning of mass points.
Processing lidar data involves systematically classifying points according to the various surfaces they represent—the ground surface, or above-ground surfaces like tree canopy and structures. The ability to view and interact with pseudo-stereopair images created from lidar time and intensity data make it possible to apply traditional photogrammetric techniques like break line delineation in a process called "lidargrammetry." One of the most exciting potentials of lidar data is the object-based image analysis and feature extraction its fusion with multispectral data makes possible.


23. Summary and Outlook
Remotely sensing image data are diverse, but most have some common characteristics. One is that the data represent measurements of electromagnetic energy (sonar is an exception to this rule). Another is that the data can be compared in terms of spatial, radiometric, spectral, and temporal resolution. We stressed that a key advantage of multispectral remote sensing is that objects that "look" the same in the one band of the electromagnetic spectrum may be easier to tell apart when viewed in multiple bands.
This chapter identified a couple of key trends in the remote sensing field. One is the miniaturization and, some would say, democratization of aerial and space-based platforms (UAVs and small satellites). Another is the emergence of object-based analysis of high resolution multispectral imagery, and the corresponding decline of pixel-based classification techniques.
Throughout the chapter, we suggested that earth imaging is analogous to desktop document scanning, only a lot more complicated. Earth's shape, rotation, and semi-transparent atmosphere, along with aircraft flightpaths and satellite orbits, necessitate geometric and radiometric corrections, as well as image enhancements. Finally, we pointed out that the desktop scanner analogy is more fitting for active remote sensing like radar and lidar than it is for passive sensors that measure solar radiation emitted by the Sun and reflected or re-emitted by Earth.
Analysts in many fields have adopted land remote sensing data for a wide array applications like land use and land cover mapping, geological resource exploration, precision farming, archeological investigations, and even validating the computational models used to predict global environmental change. Once the exclusive domain of government agencies, an industry survey suggests that the gross revenue earned by private land remote sensing firms exceeded $7 billion (U.S.) in 2010 (ASPRS, 2011).
The fact that remote sensing is first and foremost a surveillance technology cannot be overlooked. State-of-the-art spy satellites operated by government agencies, high resolution commercial sensors, and now cameras mounted on UAVs are challenging traditional conceptions of privacy. In a historical precedent, remotely sensed data were pivotal in the case of an Arizona farmer who was fined for growing cotton illegally (Kerber, 1998). Was the farmer right to claim that remote sensing constituted unreasonable search? More serious, perhaps, is the potential impact of the remote sensing industry on defense policy of the United States and other countries. Some analysts foresee that "the military will be called upon to defend American interests in space much as navies were formed to protect sea commerce in the 1700s" (Newman, 1999).
Geospatial professionals should be mindful and conscientious about the ethical implications of remote sensing technologies. However, the potential of these technologies and methods to help us to become more knowledgeable, and thus more effective stewards of our home planet, is compelling. Several challenges must be addressed before remote sensing can fulfill this potential. One is the need to produce affordable, high-resolution data suitable for local scale mapping—the scale at which most land use decisions are made. UAV-based aerial imaging seems to have great potential in this context. Another is the need to further develop object-based image analysis techniques that will improve the accuracy and cost-effectiveness of information derived from remotely sensed imagery.
Of course this brief overview cannot adequately convey the depth and dynamism of the remote sensing field. For those interested in learning more, we suggested specialized Penn State courses in remote sensing, image analysis, lidar, and even unmanned aerial systems (UAS). Meanwhile, if you really want to geek out, check out the Earth Observation Portal, which provides a searchable database of over 600 in-depth articles of satellite missions from 1959 to 2020, as well as a complementary database of airborne sensors containing detailed information of almost 40 flight campaigns from the last 20 years.

24. Bibliography
Chapter 9: Integrating Geographic Data
1. Overview
Geographic data are expensive to produce and maintain. Data often accounts for the lion's share of the cost of building and running geographic information systems. The expense of GIS is justifiable when it gives people the information they need to make wise choices in the face of complex problems. In this chapter, we'll consider one such problem: the search for suitable and acceptable sites for low level radioactive waste disposal facilities. Two case studies will demonstrate that GIS is very useful indeed for assimilating the many site suitability criteria that must be taken into account, provided that the necessary data can be assembled in a single, integrated system. The case studies will allow us to compare vector and raster approaches to site selection problems.
The ability to integrate diverse geographic data is a hallmark of mature GIS software. The know-how required to accomplish data integration is also the mark of a truly knowledgeable GIS user. What knowledgeable users also recognize, however, is that while GIS technology is well suited to answering certain well-defined questions, it often cannot help resolve crucial conflicts between private and public interests. The objective of this final, brief chapter is to consider the challenges involved in using GIS to address a complex problem that has both environmental and social dimensions.
Objectives
Students who successfully complete Chapter 9 should be able to:
- recognize the characteristics of geographic data that must be taken into account to overlay multiple data layers;
- compare and contrast vector and raster approaches to site suitability studies;
- gave realistic expectations about what geographic data analysis can achieve.
"Try This!" Activities
Take a minute to complete any of the Try This activities that you encounter throughout the chapter. These are fun, thought provoking exercises to help you better understand the ideas presented in the chapter.

2. Context
This section sets a context for two case studies that follow. First, I will briefly define low-level radioactive waste (LLRW). Then I discuss the legislation that mandated construction of a dozen or more regional LLRW disposal facilities in the U.S. Finally, I will reflect briefly on how the capability of geographic information systems to integrate multiple data "layers" is useful for siting problems like the ones posed by LLRW.
3. Low Level Radioactive Waste
According to the U.S. Nuclear Regulatory Commission (2004), LLRW consists of discarded items that have become contaminated with radioactive material or have become radioactive through exposure to neutron radiation. Trash, protective clothing, and used laboratory glassware make up all but about 3 percent of LLRW. These "Class A" wastes remain hazardous less than 100 years. "Class B" wastes, consisting of water purification filters and ion exchange resins used to clean contaminated water at nuclear power plants, remain hazardous up to 300 years. "Class C" wastes, such as metal parts of decommissioned nuclear reactors, constitute less than 1 percent of all LLRW, but remain dangerous for up to 500 years.
The danger of exposure to LLRW varies widely according to the types and concentration of radioactive material contained in the waste. Low level waste containing some radioactive materials used in medical research, for example, is not particularly hazardous unless inhaled or consumed, and a person can stand near it without shielding. On the other hand, exposure to LLRW contaminated by processing water at a reactor can lead to death or an increased risk of cancer (U.S. Nuclear Regulatory Commission, n.d.).

Figure 9.4.1 shows a bar graph and a pie chart that appear here in table form.Note that Volumes are rounded to the nearest thousand cubic feet and percentages are rounded to the nearest tenth of a percent.
| Year | Volume (Thousands of Cubic Feet) |
|---|---|
| 1985 | 2681 |
| 1986 | 1805 |
| 1987 | 1842 |
| 1988 | 1428 |
| 1989 | 1626 |
| 1990 | 1143 |
| 1991 | 1369 |
| 1992 | 1743 |
| 1993 | 792 |
| 1994 | 859 |
| 1995 | 690 |
| 1996 | 422 |
| 1997 | 319 |
| 1998 | 1419 |
| Facility Name | Cubic Feet / Percentage |
|---|---|
| Envirocare | 1080K / 76.1% |
| Barnwell | 194K / 13.7% |
| Richland | 145K / 10.2% |
Hundreds of nuclear facilities across the country produce LLRW, but only a very few disposal sites are currently willing to store it. Disposal facilities at Clive, Utah; Barnwell, South Carolina; and Richland, Washington accepted over 4,000,000 cubic feet of LLRW in both 2005 and 2006, up from 1,419,000 cubic feet in 1998. By 2008, the volume had dropped to just over 2,000,000 cubic feet (U.S. Nuclear Regulatory Commission, 2011a). Sources include nuclear reactors, industrial users, government sources (other than nuclear weapons sites), and academic and medical facilities. (We have a small nuclear reactor here at Penn State that is used by students in graduate and undergraduate nuclear engineering classes.)
4. Siting LLRW Storage Facilities
The U.S. Congress passed the Low-Level Radioactive Waste Policy Act in 1980. As amended in 1985, the Act made states responsible for disposing of the LLRW they produce. States were encouraged to form regional "compacts" to share the costs of locating, constructing, and maintaining LLRW disposal facilities. The intent of the legislation was to avoid the very situation that has since come to pass, that the entire country would become dependent on a very few disposal facilities.

State government agencies and the consultants they hire to help select suitable sites assume that few if any municipalities would volunteer to host a LLRW disposal facility. They prepare for worst-case scenarios in which states would be forced to exercise their right of eminent domain to purchase suitable properties without the consent of landowners or their neighbors. GIS seems to offer an impartial, scientific, and therefore defensible approach to the problem. As Mark Monmonier has written, "[w]e have to put the damned thing somewhere, the planners argue, and a formal system of map analysis offers an 'objective,' logical method for evaluating plausible locations" (Monmonier, 1995, p. 220). As we discussed in our very first chapter, site selection problems pose a geographic question that geographic information systems are well suited to address, namely, which locations have attributes that satisfy all suitability criteria?
5. Map Overlay Concept
Environmental scientists and engineers consider many geological, climatological, hydrological, and surface and subsurface land use criteria to determine whether a plot of land is suitable or unsuitable for a LLRW facility. Each criterion can be represented with geographic data, and visualized as a thematic map. In theory, the site selection problem is as simple as compiling onto a single map all the disqualified areas on the individual maps, and then choosing among whatever qualified locations remain. In practice, of course, it is not so simple.
There is nothing new about superimposing multiple thematic maps to reveal optimal locations. One of the earliest and most eloquent descriptions of the process was written by Ian McHarg, a landscape architect and planner, in his influential book Design With Nature. In a passage describing the process he and his colleagues used to determine the least destructive route for a new roadway, McHarg (1971) wrote:
...let us map physiographic factors so that the darker the tone, the greater the cost. Let us similarly map social values so that the darker the tone, the higher the value. Let us make the maps transparent. When these are superimposed, the least-social-cost areas are revealed by the lightest tone. (p. 34).
As you probably know, this process has become known as map overlay. Storing digital data in multiple "layers" is not unique to GIS, of course; computer-aided design (CAD) packages and even spreadsheets also support layering. What's unique about GIS, and important about map overlay, is its ability to generate a new data layer as a product of existing layers. In the example illustrated below, for example, analysts at Penn State's Environmental Resources Research Institute estimated the agricultural pollution potential of every major watershed in the state by overlaying watershed boundaries, the slope of the terrain (calculated from USGS DEMs), soil types (from U.S. Soil Conservation Service data), land use patterns (from the USGS LULC data), and animal loading (livestock wastes estimated from the U.S. Census Bureau's Census of Agriculture).

As illustrated below, map overlay can be implemented in either vector or raster systems. In the vector case, often referred to as polygon overlay, the intersection of two or more data layers produces new features (polygons). Attributes (symbolized as colors in the illustration) of intersecting polygons are combined. The raster implementation (known as grid overlay) combines attributes within grid cells that align exactly. Misaligned grids must be resampled to common formats.

Polygon and grid overlay procedures produce useful information only if they are performed on data layers that are properly georegistered. Data layers must be referenced to the same coordinate system (e.g., the same UTM and SPC zones), the same map projection (if any), and the same datum (horizontal and vertical, based upon the same reference ellipsoid). Furthermore, locations must be specified with coordinates that share the same unit of measure.
6. Pennsylvania Case Study
In response to the LLRW Policy Act, Pennsylvania entered into an "Appalachian Compact" with the states of Delaware, Maryland, and West Virginia to share the costs of siting, building, and operating a LLRW storage facility. Together, these states generated about 10 percent of the total volume of LLRW then produced in the United States. Pennsylvania, which generated about 70 percent of the total produced by the Appalachian Compact, agreed to host the disposal site.
In 1990, the Pennsylvania Department of Environmental Protection commissioned Chem-Nuclear Systems Incorporated (CNSI) to identify three potentially suitable sites to accommodate two to three truckloads of LLRW per day for 30 years. CNSI, the operator of the Barnwell South Carolina site, would also operate the Pennsylvania site for profit.

CNSI's plan called for storing LLRW in 55-gallon drums encased in concrete, buried in clay, surrounded by a polyethylene membrane. The disposal facilities, along with support and administration buildings and a visitors center, would occupy about 50 acres in the center of a 500-acre site. (Can you imagine a family outing to the Visitors Center of a LLRW disposal facility?) The remaining 450 acres would be reserved for a 500 to 1000 foot wide buffer zone.
The three-stage siting process agreed to by CNSI and the Pennsylvania Department of Environmental Protection corresponded to three scales of analysis: statewide, regional, and local. All three stages relied on vector geographic data integrated within a GIS.
7. Vector Approach
CNSI and its subcontractors adopted a vector approach for its GIS-based site selection process. When the process began in 1990, far less geographic data was available in digital form than it is today. Most of the necessary data was available only as paper maps, which had to be converted to digital form. In one of its interim reports, CNSI described two digitizing procedures used, "digitizing" and "scanning." Here's how it described "digitizing:"
In the digitizing process, a GIS operator uses a hand-held device, known as a cursor, to trace the boundaries of selected disqualifying features while the source map is attached to a digitizing table. The digitizing table contains a fine grid of sensitive wire imbedded within the table top. This grid allows the attached computer to detect the position of the cursor so that the system can build an electronic map during the tracing. In this project, source maps and GIS-produced maps were compared to ensure that the information was transferred accurately. (Chem Nuclear Systems, 1993, p. 8).
One aspect overlooked in the CNSI description is that operators must encode the attributes of features as well as their locations. Some of you know all too well that tablet digitizing (illustrated at left in Figure 9.8.1, below) is an extraordinarily tedious task, so onerous that even student interns resent it. One wag here at Penn State suggested that the acronym "GIS" actually stands for "Getting it (the data) In Stinks." You can substitute your own "S" word if you wish.

Compared to the drudgery of tablet digitizing, electronically scanning paper maps seems simple and efficient. Here's how CNSI describes it:
The scanning process is more automated than the digitizing process. Scanning is similar to photocopying, but instead of making a paper copy, the scanning device creates an electronic copy of the source map and stores the information in a computer record. This computer record contains a complete electronic picture (image) of the map and includes shading, symbols, boundary lines, and text. A GIS operator can select the appropriate feature boundaries from such a record. Scanning is useful when maps have very complex boundaries lines that can not be easily traced. (Chem Nuclear Systems, Inc., 1993, p. 8)
I hope you noticed that CNSI's description glosses over the distinction between raster and vector data. If scanning is really as easy as they suggest, why would anyone ever tablet-digitize anything? In fact, it is not quite so simple to "select the appropriate feature boundaries" from a raster file, which is analogous to a remotely sensed image. The scanned maps had to be transformed from pixels to vector features using a semi-automated procedure called raster to vector conversion, otherwise known as "vectorization." Time-consuming manual editing is required to eliminate unwanted features (like vectorized text), correct digital features that were erroneously attached or combined, and to identify the features by encoding their attributes in a database.
In either the vector or raster case, if the coordinate system, projection, and datums of the original paper map were not well defined, the content of the map first had to be redrawn, by hand, onto another map whose characteristics are known.
8. Stage One: Statewide Screening
CNSI considered several geological, hydrological, surface and subsurface land use criteria in the first stage of its LLRW siting process. [View a table that lists all the Stage One criteria.] CNSI's GIS subcontractors created separate digital map layers for every criterion. Sources and procedures used to create three of the map layers are discussed briefly below.

One of the geological criteria considered was carbonate lithology. Limestone and other carbonate rocks are permeable. Permeable bedrock increases the likelihood of groundwater contamination in the event of a LLRW leak. Areas with carbonate rock outcrops were therefore disqualified during the first stage of the screening process. Boundaries of disqualified areas were digitized from the 1:250,000-scale Geologic Map of Pennsylvania (1980). What concerns would you have about data quality, given a 1:250,000-scale source map?

Analysts needed to make sure that the LLRW disposal facility would never be inundated with water in the event of a coastal flood or a rise in sea level. To determine disqualified areas, CNSI's subcontractors relied upon the Federal Emergency Management Agency's Flood Insurance Rate Maps (FIRMs). The maps were not available in digital form at the time and did not include complete metadata. According to the CNSI interim report, "[t]he 100-year flood plains shown on maps obtained from FEMA ... were transferred to USGS 7.5-minute quad sheet maps. The 100-year floodplain boundaries were digitized into the GIS from the 7.5-minute quad sheet maps." (Chem Nuclear Systems, 1991, p. 11) Why would the contractors go to the trouble of redrawing the floodplain boundaries onto topographic maps prior to digitizing?

Areas designated as "exceptional value watersheds" were also disqualified during Stage One. Pennsylvania legislation protected 96 streams. Twenty-nine additional streams were added during the site screening process. "The watersheds were delineated on county [1:50,000 or 1:100,000-scale topographic] maps by following the appropriate contour lines. Once delineated, the EV stream and its associated watershed were digitized into the GIS." (Chem Nuclear Systems, 1991, p. 12) What digital data sets could have been used to delineate the watersheds automatically, had the data been available?
After all the Stage One maps were digitized, georegistered, and overlayed, approximately 23 percent of the state's land area was disqualified.
9. Stage Two: Regional Screening
CNSI considered additional disqualification criteria during the second, "regional" stage of the LLRW siting process. [View a table that lists all the Stage Two criteria.] Some of the Stage Two criteria had already been considered during Stage One, but were now reassessed in light of more detailed data compiled from larger-scale sources. In its interim report, CNSI had this to say about the composite disqualification map shown below:
When all the information was entered in to Stage Two database, the GIS was used to draw the maps showing the disqualified land areas. ... The map shows both additions/refinements to the Stage One disqualifying features and those additional disqualifying features examined during Stage Two. (Chem Nuclear Systems, 1993, p. 19)

CNSI added this disclaimer:
The Stage Two Disqualifying maps found in Appendix A depict information at a scale of 1:1.5 million. At this scale, one inch on the map represents 24 miles, or one mile is represented on the map by approximately four one-hundreds of an inch. A square 500-acre area measures less than one mile on a side. Printing of such fine detail on the 11" × 17" disqualifying maps was not possible, therefore, it is possible that small areas of sufficient size for the LLRW disposal facility site may exist within regions that appear disqualified on the attached maps. [Emphasis in the original document] The detailed boundary information for these small areas is retained within the GIS even though they are not visually illustrated on the maps. (Chem Nuclear Systems, 1993, p. 20)
As I mentioned back in Chapter 2, CNSI representatives took some heat about the map scale problem in public hearings. Residents took little solace in the assertion that the data in the GIS were more truthful than the data depicted on the map.
10. Stage Three: Local Disqualification
Many more criteria were considered in Stage Three. [View a table that lists all the Stage Three criteria.] At the completion of the third stage, roughly 75 percent of the state's land area had been disqualified.
One of the new criteria introduced in Stage Three was slope. Analysts were concerned that precipitation runoff, which increases as slope increases, might increase the risk of surface water contamination should the LLRW facility spring a leak. CNSI's interim report (1994a) states that "[t]he disposal unit area which constitutes approximately 50 acres ... may not be located where there are slopes greater than 15 percent as mapped on U.S. Geological Survey (USGS) 7.5-minute quadrangles utilizing a scale of 1:24,000 ..." (p. 9).
Slope is change in terrain elevation over a given horizontal distance. It is often expressed as a percentage. A 15 percent slope changes at a rate of 15 feet of elevation for every 100 feet of horizontal distance. Slope can be measured directly on topographic maps. The closer the spacing of elevation contours, the greater the slope. CNSI's GIS subcontractors were able to identify areas with excessive slope on topographic maps using plastic templates called "land slope indicators" that showed the maximum allowable contour spacing.
Fortunately for the subcontractors, 7.5-minute USGS DEMs were available for 85 percent of the state (they're all available now). Several algorithms have been developed to calculate slope at each grid point of a DEM. As described in chapter 7, the simplest algorithm calculates slope at a grid point as a function of the elevations of the eight points that surround it to the north, northeast, east, southeast, and so on. CNSI's subcontractors used GIS software that incorporated such an algorithm to identify all grid points whose slopes were greater than 15 percent. The areas represented by these grid points were then made into a new digital map layer.
Try This!
You can create a slope map of the Bushkill PA quadrangle with Global Mapper (dlgv32 Pro) software.
- Launch Global Mapper.
- Open the file "bushkill_pa.dem" that you downloaded earlier (either the 10-meter or 30-meter version).
- Change from the default "HSV" shader to the "Slope" shader.

By default, pixels with 0 percent slope are lightest, and pixels with 30 percent slope or more are darkest. You can adjust this at Tools > Configure > Shader Options.
Notice that the slope symbolization does not change even as you change the vertical exaggeration of the DEM (Tools > Configure > Vertical Options).

11. Buffering
Several of the disqualification criteria involve buffer zones. For example, one disqualifying criterion states that "[t]he area within 1/2 mile of an existing important wetland ... is disqualified." Another states that "disposal sites may not be located within 1/2 mile of a well or spring which is used as a public water supply." (Chem-Nuclear Systems, 1994b). As I mentioned in the first chapter (and as you may know from experience), buffering is a GIS procedure by which zones of specified radius or width are defined around selected vector features or raster grid cells.
Like map overlay, buffering has been implemented in both vector and raster systems. The vector implementation involves expanding a selected feature or features, or producing new surrounding features (polygons). The raster implementation accomplishes the same thing, except that buffers consist of sets of pixels rather than discrete features.

12. New York Case Study
Like Pennsylvania, the State of New York was compelled by the LLRW Policy Act to dispose of its waste within its own borders. New York also turned to GIS in the hope of finding a systematic and objective means of determining an optimal site. Instead of the vector approach used by its neighbor, however, New York opted for a raster framework.

Mark Monmonier, a professor of geography at Syracuse University (and a Penn State alumnus), has written that the list of siting criteria assembled by the New York Department of Environmental Conservation (DEC) was "an astute mixture of common sense, sound environmental science, and interest-group politics" (1995, p. 226). Source data included maps and attribute data produced by the U.S. Census Bureau, the New York Department of Transportation, and the DEC itself, among others. The New York LLRW Siting Commission overlaid the digitized source maps with a grid composed of cells that corresponded to one square mile (640 acres; slightly larger than the 500 acres required for a disposal site) on the ground. As illustrated above, the Siting Commission's GIS subcontractors then assigned each of the 47,224 grid cells a "favorability" score for each criterion. The process was systematic, but hardly objective, since the scores reflected social values (to borrow the term used by McHarg).

To acknowledge the fact that some criteria were more important than others, the Siting Commission weighted the scores in each data layer by multiplying them all by a constant factor. Like the original integer scores, the weighting factors were a negotiated product of consensus, not of objective measurement. Finally, the commission produced a single set of composite scores by summing the scores of each raster cell through all the data layers. A composite favorability map could then be produced from the composite scores. All that remained was for the public to embrace the result.
13. Outcomes
To date, neither Pennsylvania nor New York has built an LLRW disposal facility. Both states gave up on their unpopular sitting programs shortly after Republicans replaced Democrats in the 1994 gubernatorial elections.
The New York process was derailed when angry residents challenged proposed sites on account of inaccuracies discovered in the state's GIS data, and because of the state's failure to make the data accessible for citizen review in accordance with the Freedom of Information Act (Monmonier, 1995).
Pennsylvania's $37 million siting effort succeeded in disqualifying more than three-quarters of the state's land area but failed to recommend any qualified 500-acre sites. With the volume of its LLRW decreasing, and the Barnwell South Carolina facility still willing to accept Pennsylvania's waste shipments, the search was suspended "indefinitely" in 1998.
To fulfill its obligations under the LLRW Policy Act, Pennsylvania has initiated a "Community Partnering Plan" that solicits volunteer communities to host a LLRW disposal facility in return for jobs, construction revenues, shares of revenues generated by user fees, property taxes, scholarships, and other benefits. The plan has this to say about the GIS site selection process that preceded it: "The previous approach had been to impose the state's will on a municipality by using a screening process based primarily on technical criteria. In contrast, the Community Partnering Plan is voluntary." (Chem Nuclear Systems, 1996, p. 3)
The New York and Pennsylvania state governments turned to GIS because it offered an impartial and scientific means to locate a facility that nobody wanted in their backyard. Concerned residents criticized the GIS approach as impersonal and technocratic. There is truth to both points of view. Specialists in geographic information need to understand that while GIS can be effective in answering certain well-defined questions, it does not ease the problem of resolving conflicts between private and public interests.
Meanwhile, a Democrat replaced a Republican as governor of South Carolina in 1998. The new governor warned that the Barnwell facility might not continue to accept out-of-state LLRW. "We don't want to be labeled as the dumping ground for the entire country," his spokesperson said (Associated Press, 1998).
No volunteer municipality has yet come forward in response to Pennsylvania's Community Partnering Plan. If the South Carolina facility does stop accepting Pennsylvania's LLRW shipments, and if no LLRW disposal facility is built within the state's borders, then nuclear power plants, hospitals, laboratories, and other facilities may be forced to store LLRW on site. It will be interesting to see if the GIS approach to site selection is resumed as a last resort, or if the state will continue to up the ante in its attempts to attract volunteers, in the hope that every municipality has its price. If and when a volunteer community does come forward, detailed geographic data will be produced, integrated, and analyzed to make sure that the proposed site is suitable, after all.
Try This!
To find out about LLRW-related activities where you live, use your favorite search engine to search the Web on "Low-Level Radioactive Waste [your state or area of interest]". If GIS is involved in your state's LLRW disposal facility site selection process, your state agency that is concerned with environmental affairs is likely to be involved.

14. Conclusion
Site selection projects like the ones discussed in this chapter require the integration of diverse geographic data. The ability to integrate and analyze data organized in multiple thematic layers is a hallmark of geographic information systems. To contribute to GIS analyses like these, you need to be both a knowledgeable and skillful GIS user. The objective of this text, and the associated Penn State course, has been to help you become more knowledgeable about geographic data.
Knowledgeable users are well versed in the properties of geographic data that need to be taken into account to make data integration possible. Knowledgeable users understand the distinction between vector and raster data, and know something about how features, topological relationships among features, attributes, and time can be represented within the two approaches. Knowledgeable users understand that in order for geographic data to be organized and analyzed as layers, the data must be both orthorectified and georegistered. Knowledgeable users look out for differences in coordinate systems, map projections, and datums that can confound efforts to georegister data layers. Knowledgeable users know that the information needed to register data layers is found in metadata.
Knowledgeable users understand that all geographic data are generalized, and that the level of detail preserved depends upon the scale and resolution at which the data were originally produced. Knowledgeable users are prepared to convince their bosses that small-scale, low resolution data should not be used for large-scale analyses that require high resolution results. Knowledgeable users never forget that the composition of the Earth's surface is constantly changing, and that unlike fine wine, the quality of geographic data does not improve over time.
Knowledgeable users are familiar with the characteristics of the "framework" data that make up the U.S. National Spatial Data Infrastructure, and are able to determine whether these data are available for a particular location. Knowledgeable users recognize situations in which existing data are inadequate, and when new data must be produced. They are familiar enough with geographic information technologies such as GPS, aerial imaging, and satellite remote sensing that they can judge which technology is best suited to a particular mapping problem.
And knowledgeable users know what kinds of questions GIS is, and is not, suited to answer.
