3.2.5: Instantaneous Stripping Ratio
The stripping ratio (SR) refers to the amount of waste material that must be removed for a given amount of ore. The Instantaneous Stripping Ratio (ISR) is the stripping ratio for a given push back, where a tiny slice of material, i.e., ore and/or waste, is removed from a pit wall. This section presents the ISR calculation for a steeply pitching deposit.
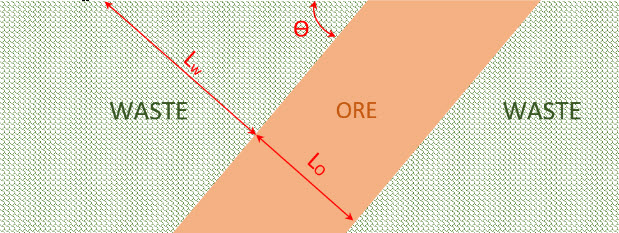
Assume an idealized tabular and steeply pitching orebody that outcrops at the surface and dips to the left at ϴ degrees (Figure 3.2.10). Assume that the ore extends down to considerable depth, and that open-pit mining will be used to extract ore. When open-pit mining is no longer economical, an underground mining method will be used to recover the ore. Therefore, we will need to calculate the point at which we will cease surface mining and either go underground or close the mine.
The over-lying waste, i.e., the non-mineral-bearing rock, must be removed to uncover and mine the ore. The shape and size of the pit depends upon economic, engineering, and production factors. Assuming all other factors to be constant, as the selling price of the ore increases, the pit size will increase.
If you were going to calculate the ISR for a “real” orebody for which you had drillhole data, you would utilize one of the computer software packages, such as Carlson. Here the purpose is to teach you the principles, so we are going to make some assumptions to simplify the calculations, and to better illuminate the procedure without getting buried in the math. The assumptions are as follows.
- The seam thickness is constant. The orebody thickness is represented by the length of the ore section (Lo) in the previous diagram. Note that the length of the waste section (Lw) increases as our pit advances deeper. Therefore, as we advance, more of the waste will have to be removed to expose a unit of ore, as shown in the next diagram.
- The density of ore and waste are the same.
- All slices have the same strip width (Ws).
- We are looking at a two-diminsional slice of the Earth’s crust. Obviously, the ore and overburden continue into the page and go on for some distance. For our purposes here, we will assume that they go into the page for a distance of 1 unit.
- The slices of the material are mined out perpendicular to the orebody.
Watch this video (3:11) on an explanation of the instantaneous stripping ratio.
Later in this section, I will explain how each of these assumptions affects the calculations. However, it would be instructive for you to pause for a moment and think about each assumption.
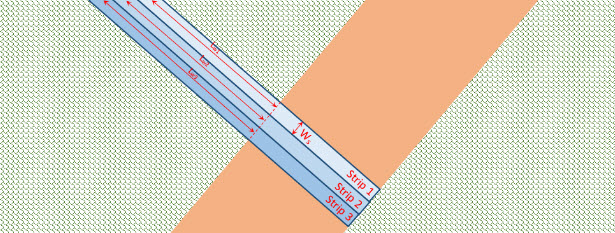
Now, let’s calculate the ISR for strip 1:
where T is strip thickness, L is strip length, W is strip width and ρ is material density.
Since the density, width, and thickness of the ore and waste are assumed to be equal, this equation reduces to:
Assume that the ore seam thickness is 40 ft and the length of the waste slice on top of the ore in strips 1, 2 and 3 is 45, 50 and 55, respectively. The ISR for these three strips is calculated as:
This simplified example has illustrated how the length of waste and ore sections will impact the ISR. In a mine, there will be differences in the density of the ore and waste materials. However, the difference can be trivial in some cases. In fact, a real-world example is where there are several waste types in the slice, and the waste materials have densities that are each different from the ore. Therefore, the calculation of ISR using the length ratio does not work. Instead, a generalized IRS calculation must be defined as:
where there are i different waste material types in the strip.
If the density differences are not drastic, the simplified form of the calculation will give you a rough estimate of the ISR. If you need more accurate values with higher accuracy level, then you should consider all other parameters in your calculations. Of course, as I mentioned earlier, if you are doing a complex and “real-world” case, you will probably be using a software package; and then, accounting for the myriad of details becomes easier.
By the way, please note that the ISR is independent of the deposit's dip angle.
For this discussion, we have used an orebody of uniform shape and plunging at some angle θ. But what of a deposit with an irregular shape? The same process applies. Therefore, regardless of the shape of the orebody, the above equation can be used to determine ISR for a strip extracted from the side wall of the pit. It should be also noted that different units can be used to express the ISR.
The most popular units for the ISR are tons of waste removed/ton of ore exposed, ft of waste removed/ft of ore exposed, and yd3 of waste removed/ton of ore exposed. The latter is the most common unit in many types of nonmetal operations because there is no value to know the weight of the waste, unless it poses a limit to the trucks. Therefore, the density of waste material does not come into play in the calculations. If there is an issue with a weight limit in the haul trucks, then the tons of waste/ton of ore is an appropriate unit for the ISR or SR.