Lessons
Lesson 1: Introduction to Petroleum and Natural Gas Engineering
1.0: Lesson Overview
Learning Objectives
By the end of this lesson, you should be able to:
- name and describe the different reservoir fluids found in a hydrocarbon accumulation;
- identify and explain the roles of the different sectors in the modern oil and gas industry;
- name the products derived from oil and gas production;
- list and explain the roles of the different disciplines within the petroleum and natural gas engineering profession; and
- summarize the current and future challenges in the petroleum and natural gas engineering profession.
Lesson 1 Checklist
| To Read |
|
|
|---|---|---|
| To Do |
|
|
| Note | You must score 100% on the Academic Integrity & Plagiarism Awareness Quiz and the Orientation Knowledge Quiz to unlock the remaining Canvas lesson modules. |
Please refer to the Calendar in Canvas for specific time frames and due dates.
Questions?
If you have questions, please feel free to post them to the Course Q&A Discussion Board in Canvas. While you are there, feel free to post your own responses if you, too, are able to help a classmate.
1.1: Petroleum and Natural Gas
The word “Petroleum” has its origin in the Greek words “petra” for “rock” and “oleum” for “oil”. Petroleum, or crude oil, is a naturally occurring liquid found in porous rocks (reservoirs) below the earth’s surface. It is an organic material comprised of hydrocarbon molecules (molecules formed by hydrogen and carbon atoms) with possible inorganic contaminates, such as nitrogen (N2), carbon dioxide (CO2), hydrogen sulfide (H2S), and others.
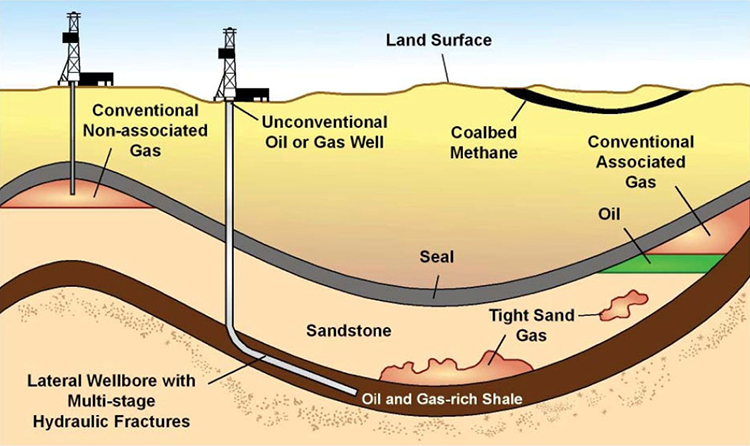
Crude oil is found in subsurface rock formations known as oil reservoirs. It is typically found in the presence of natural gas (associated natural gas). Associated natural gases are hydrocarbon gases that co-exists with the crude oil and may be present as: (1) gas dissolved in the crude oil (solution gas), (2) a distinct gas phase in contact with the crude oil (free gas), or (3) both. Natural gas may also exist with no crude oil present (non-associated gas) in natural gas reservoirs. In the context just described, the terms “associated gas” and “non-associated gas” refer to the association of the gas with a liquid hydrocarbon phase. This is illustrated in Figure 1.01.
1.2: Oil and Gas Industries
The role of the International and U.S. Domestic Oil and Gas Industries is to perform the safe, environmentally sound, and efficient discovery, extraction, transport, refining, and marketing of petroleum and natural gas and their refined products. Petroleum and natural gas engineers typically work to extract the crude oil and natural gas from the subsurface reservoirs and also have a secondary role supporting exploration geologists in the discovery of new oil and gas reservoirs.
The oil and gas industry can be classified into three broad segments: the upstream, the mid-stream, and the downstream sectors of the industry. This classification system is based on the direction in which crude oil and natural gas flow from the subsurface reservoirs (upstream sector) to the refineries and the markets (downstream sector) and, eventually, the consumers.
The upstream sector of the oil and gas industry is responsible for the discovery, extraction, and field processing of the crude oil and natural gas. As such, petroleum and natural gas engineers typically work in this sector of the industry. In this sector, petroleum and natural gas engineers work with geologists, geophysicists, other engineering disciplines (e.g., mechanical and chemical engineers), and other petroleum professionals (e.g., petrophysicists, paleontologists, etc.) to extract the crude oil and natural gas and to process the produced fluids to the specifications required by the field export systems (pipelines, tanker ships, etc.).
The mid-stream sector of the oil and gas industry is responsible for the export of the crude oil and natural from the field locations and for the transport of these products to the refineries. These refineries may be continents away from the original oil and gas fields. This transport process may occur onshore using pipelines, trains, or tanker trucks; over oceans and seaways using large tanker ships; and on inland lakes and waterways using smaller barges.
The downstream sector of the industry is responsible for the storage, refining, and marketing of the refined products to the consumers. Storage of the oil and gas may occur on the surface in “tank farms,” underground in old, abandoned oil and gas reservoirs, or in engineered, subsurface formations (e.g., hollowed out salt caverns). Storage may be required for crude oil as an unrefined inventory awaiting processing in a refinery or for storage as a refined product during seasonal lows in demand caused by the weather (e.g., heating fuels). Refining is the process of converting raw crude oil and natural gas into products in demand by industrial or individual consumers.
The international and U. S. domestic oil and gas industries form an integral part of the global economy. Oil and gas production influence all industrial sectors and geographical regions of the world, either as producers, consumers, or both. Figure 1.02 shows the energy mix in the United States by major primary energy source in 2015.
Global energy consumption (Figure 1.03) has a comparable energy mix as in the U.S..
Besides providing fuels to run automobiles, planes, ships or machinery, the primary energy sources shown in Figures 1.02 and 1.03 are also used to power electrical generation plants to provide secondary energy sources to consumers.
In addition to fuels, refined crude oil and natural gas provide other valuable products including kerosene for illumination, lubricants for machinery, butane and propane for recreational and industrial uses, asphalts for road construction, and feedstocks for the petrochemical industry. Figure 1.04 shows the typical product yield from a standard 42 gallon barrel of crude oil.
Thanks to "processing gains" at today's refineries,
a 42 gallon barrel of crude oil can make an average of
44.2 gallons of product, but very little of it is lubricant.
1.3: Oil and Gas Professions
The petroleum and natural gas engineering profession is normally divided into three major areas of specialization based on the tasks assigned to the engineer. These areas are: Drilling or Drilling and Completions (D&C) Engineers, Production Engineers, and Reservoir Engineers.
Drilling Engineers, or Drilling and Completions Engineers
Drilling Engineers, or Drilling and Completions Engineers, are responsible for planning, designing, and executing the drilling operations of a well. Drilling a well may take several years to properly plan. This is because of the depths and quality of the steel tubulars (drill pipe, casing, and production tubing) that are required by the oil and gas industry. For example, a ten-well drilling campaign to a total depth of 12,000 ft per well in a high temperature, high pressure, highly corrosive environment will take several miles of high-grade steel tubulars which cannot be purchased “off-the-shelf” from steel manufactures. These items are “Long Lead Time” items in the well design and must be considered years in advance of the actual drilling operations. In fact, an aggressive drilling campaign in a single oilfield may exhaust the world’s supply of a particular steel grade for several years. Coordinating the design of the well with the suppliers of the well components is an integral part of the planning process performed by the drilling engineer.
During drilling operations, the drilling engineer must also determine the appropriate drilling fluids to use to allow for safe drilling operations and select the appropriate drill bits to use to allow for optimal drilling efficiency (cost, speed, etc.). The drilling engineer must also decide on the appropriate depths to set casing and the appropriate steel grades of the casing to protect both the wellbore and the environment (Casing is used to isolate the well from the various geologic rock formations and aquifers that a well encounters and to isolate the individual rock formations from each other.).
Once the wellbore has reached the predetermined total depth and the final casing string has been cemented in place, the drilling engineer works with the production engineer to implement the well’s completion. The well completion is the portion of the well that connects the wellbore to the reservoir. This aspect of the well design has many considerations in order to achieve the long-term objectives of the well. Important considerations of a completion design include: selecting the appropriate size and grade of the production tubing; determining the need to stimulate the reservoir (hydraulic fracturing, acidizing, etc.) to allow for economical production rates from the reservoir to the well, and selecting the appropriate artificial lift system (natural lift, pump, gas lift, etc.) to aid in “lifting” the produced fluids from the reservoir to the surface.
Production Engineer
The role of the Production Engineer is to monitor individual wells or groups of wells to ensure that they are producing (or, in the case of injection wells, injecting) optimally. Over time, downhole equipment may fail, produced hydrocarbons fluids may deposit waxes or asphaltenes on downhole equipment and tubing, minerals in produced water may create a scale on downhole equipment and tubing, steel tubing may corrode or erode, etc. All of these phenomena can negatively affect the performance of the well. In addition, due to changing reservoir conditions, equipment and tubing sizes that were optimal at the beginning of production may be suboptimal at depleted reservoir conditions.
To monitor wells, production engineers may install permanent downhole sensing equipment to continuously observe well performance in real time. In addition, the production engineer may perform discrete tests on the well by sending monitoring tools down the well to observe well performance as a “snapshot in time.” These discrete tests can either be (1) well logs, where tools are sent downhole that measure properties of interest to the engineer such as flow rates, temperatures, internal tubing diameters etc., or (2) well tests, where pressure gauges are sent downhole, well rates are adjusted in a controlled, known manner, and the corresponding pressure responses are recorded and analyzed. The analysis of the pressure responses during a well test provides a valuable insight into the near-well performance of the reservoir.
If a problem is identified with the well, it is then up to the production engineer to determine the appropriate remedial actions to resolve the issue. These well remediations may take the form of simple “wireline workovers” or more complex “major rig workovers (MRWO).” In a wireline workover, all work is performed with tools lowered into the well at the end of an electrical cable (wireline). Using a wireline, perforations (connections to the reservoir) can be added, tubing plugs can be set or retrieved, packers (downhole equipment used to isolate reservoir zones) can be set or retrieved, valves can be opened or closed, etc. In a major rig workover, a drilling rig or specialized workover rig is moved on location above the well and is used to re-enter the well to retrieve the original tubing or completion equipment, cement off depleted reservoir zones (to establish zonal isolation), or to restimulate the well.
In addition to monitoring wells and performing well remediations, production engineers look after the artificial lift systems used in the well. Typical artificial lift systems include beam pumps (see Figure 1.05), downhole electrical submersible pumps (ESPs), or gas lift.
By the nature of their jobs, production engineers interact with oilfield service providers to ensure that the appropriate technologies are applied to optimize well production or injection.
Reservoir Engineers
While production engineers focus on individual wells or groups of wells, Reservoir Engineers attempt to optimize production of the reservoir as a whole. Reservoir engineers work with geologists, drilling engineers, and production engineers to ensure that the entire reservoir system is running optimally. Typical tasks performed by reservoir engineers include: working with geologists to determine the original-oil-in-place in the reservoir and identifying future well locations; identifying the drive mechanisms (the physical phenomena which cause the oil and gas to migrate to the production wells); estimating the reservoir reserves (volumes of oil and gas that can be technically and economically extracted from the reservoir), recommending the appropriate development plans for a reservoir (and recognizing when it is time to modify a plan); forecasting future production and injection rates from the reservoir in its entirety; and determining the need for applying Improved Oil Recovery (IOR) or Enhanced Oil Recovery (EOR) methods.
Typically, petroleum engineering students have the option to choose which of these areas of specialization they would like to undertake during their careers; however, the Law of Supply and Demand also works in the petroleum and natural gas engineering job market. For example, a company in need of the services of Production Engineers will hire engineers with this particular skill set. Consequently, some degree of flexibility among these three areas of specialization is required when searching for an entry-level position in the oil and gas industry.
The modern approach to crude oil and natural gas extraction is the Reservoir Management approach. Reservoir Management is a team based methodology in which all disciplines (geologists, drilling engineers, production engineers, reservoir engineers, and other petroleum professionals) work together toward the common goal of efficient, safe, and environmentally friendly production of oil and gas.
Current status and future challenges of Reservoir Management can be summarized with the Resource Triangle [1]. Figure 1.06 shows the current status of Reservoir Management in the Resource Triangle. In this figure, the easy-to-produce resources (crude oil and natural gas) are at the top of the triangle. These resources are characterized by good, high-quality reservoir rock (high storage capacity and ability to easily transmit fluids) which are saturated with highly mobile (easily flowing) fluids. The base of the triangle represents the more difficult-to-produce or yet to be discovered resources. While the resources at the base of the triangle are more difficult to find and extract, they can still be produced at higher energy prices (allowing for more capital to be spent to find, drill, and apply cutting-edge technologies for their extraction) or with improvements in current technology.
Figure 1.06 also illustrates the status of producing assets in known, mature basins. Due to the time-scales of oil and gas production, we are still producing from fields that were discovered in the early to mid-twentieth century. Consequently, some of the equipment installed in the field may be legacy equipment (then-current technologies) and all of the pre-production, baseline data for these fields were acquired using legacy data acquisition technologies. This is the situation in which many newly graduated petroleum and natural gas engineers may find themselves. Consequently, these engineers must be well versed in past, present, and emerging production technologies and analysis techniques.

The Resource Triangle can also be used to illustrate the future challenges in Reservoir Management, as in Figure 1.07.

Figure 1.07 shows the same “easy-to-produce” and “difficult-to-produce” resources as in Figure 1.06. All of these resources, including the “easy-to-produce” resources, have various challenges associated with them. It is the role of petroleum and natural gas engineers to devise cost-effective solutions to these challenges.
Typically, even in the best quality reservoirs, only one-third of the original-oil-in-place can be recovered using conventional production technologies (typically 30 – 35 percent recovery efficiencies). Recovery efficiencies for natural gas reservoirs are normally much greater (typically 65 – 85 percent recovery efficiencies). The remaining in-place oil and gas after the application of conventional production technologies, therefore, represents a significant target for additional recovery.
[1] Reference: MRS Bulletin: Factors That Will Influence Oil and Gas Supply and Demand in the 21st Century [7]
1.4: Improved Oil Recovery and Enhanced Oil Recovery Methods
Improved Oil Recovery (IOR) and Enhanced Oil Recovery (EOR) Methods are methods used to target the resources not capable of being produced with conventional production methods. IOR is defined as any recovery method used to improve oil recovery above the use of non-stimulated, naturally-flowing vertical production wells (Please note that with this definition, each reservoir will have a different baseline because each reservoir will respond differently to the application of these wells). This baseline represents the simplest production technology available to the petroleum and natural gas engineer and was a common development option up to the 1960s – 1970s and often resulted in recovery efficiencies of less than ten percent.
This definition of IOR encompasses a wide variety of production technologies including additional vertical wells (infill drilling) or complex well designs (deviated, or slanted, wells; horizontal, or single-lateral, wells; multi-lateral wells), well stimulation (hydraulic fracturing and acidizing), artificial lift (beam pumps, ESPs, and gas lift), secondary recovery methods (waterflooding and gas flooding), and EOR (thermal recovery, miscible displacement, and chemical flooding).
This definition of IOR allows for the use of additional vertical wells for greater well coverage (infill drilling) than considered in the initial development plan or the use of more complex well designs to improve well performance from a single surface location. Figure 1.08 shows some of the more advanced well designs used in the current Reservoir Management. As discussed earlier, the design and execution of these complex wells is the task of the drilling engineer.

Well Stimulation
Well stimulation is an IOR technology that is used to clean well perforations and improve the flow capacity of the reservoir rock in the near-well vicinity. The two most common well stimulation methods are hydraulic fracturing and acidizing. Hydraulic fracturing, or frac’ing, refers to the high-pressure injection of a fracturing fluid, typically water (slickwater), gas, or gel, into a reservoir causing the rock to mechanically fail or fracture. Injection of the fracturing fluid is normally followed by the injection of a proppant slurry, composed of natural sand or man-made ceramic beads, used to prop-open the induced fractures once pressure is relieved after the well stimulation treatment. Hydraulic fracturing can be applied to most rock lithologies, including sandstones, carbonates (limestones and dolomites), coals, and shales.
Acidizing
Acidizing is a well technology that uses the injection of an acid solution into a porous reservoir to dissolve any residual drilling fluids or natural sediments in the well perforations and the near-well vicinity. These residual drilling fluids may impair fluid flow to the well. Several variations of the acidizing process are used to stimulate a well including: matrix acidizing where the acid solution is pumped into the reservoir below the fracture pressure (or parting pressure) to clean pores near the well and acid-fracturing where an acidic fracturing fluid is injected above the fracture pressure in order to simultaneously fracture the reservoir and dissolve the formation (creating flow channels linking the rock to the fracture). Matrix acidizing is typically used in sandstone and carbonate reservoirs; while acid-fracturing is used in carbonate reservoirs which are susceptible to breakdown by acid.
Artificial Lift
Artificial lift was discussed briefly and is defined as an IOR technology used to ”lift” reservoir fluids once they enter the well. Early in the life of a well, the natural pressure in the reservoir is great enough to overcome gravity and to push fluids to the well and up the well to the surface. This is referred to as natural flow or natural lift.
As pressure is depleted from the reservoir by the withdrawal of oil, gas, and water (comparable to letting the air out of a balloon), the natural energy in the reservoir can no longer overcome the weight of the produced fluids and cannot force them up the production tubing. At this point, the application of artificial lift is required to keep the well flowing. A second situation may also occur which requires the application of artificial lift. As oil and gas are produced from the reservoir, these fluids are often replaced by increasingly greater volumes of produced water. The produced water is a much heavier fluid than the oil and gas and the fluid column in the well may become too heavy to flow by natural means. When this occurs, artificial lift is required to continue to produce the well. As discussed earlier, the tasks of well stimulation and artificial lift fall to production engineers.
Secondary Recovery
Secondary Recovery is an IOR process used for increasing the recovery efficiency of many oilfields. In this context, Primary Recovery refers to Reservoir Management processes which deplete the reservoir energy from the natural drive mechanisms associated with the reservoir. In secondary recovery, water or natural gas are injected into the reserve to provide an external source of reservoir energy. Waterflooding is the most common form of secondary recovery used for crude oil production.
The terms, Primary Recovery and Secondary Recovery, refer to the historical order in which oil production techniques were applied. Primary recovery was typically applied as a first stage of development to take advantage of the natural drive mechanisms in the reservoir; while secondary recovery was applied at a later stage of development to supplement the depleted natural drive mechanisms. Reservoir Engineers typically determine the design and timing of the secondary recovery operations. Most oil reservoirs require some form of secondary recovery to achieve recovery efficiencies in the range of 30 – 35 percent.
Enhanced Oil Recovery, or Tertiary Recovery
In Figure 1.07, Enhanced Oil Recovery (EOR), or Tertiary Recovery, is also applied to large reservoirs. EOR involves the injection of fluids into the reservoir, which aids in crude oil production by means other than simply supplying external reservoir energy. The baseline for EOR is the incremental production after primary and secondary production. Note that this definition of the baseline for EOR differs from that for IOR. As the terminology implies, “Tertiary Recovery” technologies were historically used after primary and secondary recovery.
The type of EOR technology to be applied to a given reservoir depends on the nature of the reservoir and the fluids that it contains: polymer solutions can be used to improve the efficiency of a waterflood; miscible fluids or surface active agents (surfactants, or soup solutions) can be injected to reduce capillary forces (one of the forces that entrap crude oil in the capillaries in the reservoir); or steam can be injected into heavy oil reservoirs to reduce the viscous forces (another force that entraps crude oil) required to displace the oil. Again, the design and timing of an EOR project typically fall to the reservoir engineer.
Figure 1.07 also illustrates a current trend in Reservoir Management: the use of “Smart Technologies.” Smart technologies are capable of sensing changing reservoir conditions and modifying production characteristics in real time to continuously improve reservoir performance.
The very base of the Resource Triangle, “Emerging Frontiers,” may sound somewhat exotic; however, the last “emerging frontier” in the oil and gas industry occurred in western Pennsylvania. This was the Shale Boom that began in the mid-2000s.
It was the application of hydraulic fracturing, in conjunction with the application of the more complex, multi-lateral well designs, which made shale reservoirs commercially viable. One such shale formation, the Marcelus shale, is a massive oil and gas bearing formation located in western Pennsylvania, Ohio, West Virginia, and New York. Oil and gas production from the Marcellus shale, along with the Barnett shale (Texas), Bakken shale (North Dakota), and the Eagle Ford shale (Texas) have significantly reduced the dependency of the United States on foreign energy sources during the last decade and is projected to continue to produce for decades to come. As with all aspects of energy production, the longevity of the shale boom will depend on future oil and gas prices.
1.5 Engineering Ethics
Throughout history, the engineering profession has played a pivotal role in generating growth and improving the quality of life of society. Due to its very nature, the engineering profession requires strict ethical standards to continue providing this growth in sustained, principled manner. The National Society of Professional Engineers has codified these ethical standards into its Code of Ethics. This ethical code is provided in the following three links:
- National Society of Professional Engineers Code of Ethics for Engineers [9] (website)
- National Society of Professional Engineers Code of Ethics for Engineers [10] (pdf)
- National Society of Professional Engineers Ethics Reference Guide [11] (pdf)
- The Society of Petroleum Engineers also has a website devoted to its Professional Code of Conduct [12]
In light of Climate Change and Global Warming, one aspect of engineering ethics that is becoming more critical to the petroleum and natural gas engineering profession is environmental stewardship. Environmental stewardship refers to the use of conservation and sustainable practices to protect the environment. This is done by using modern best practices to:
- Reduce oil spills and gas emissions with the goal of eliminating them altogether
- Minimizing the environmental footprint of all oil and gas extraction operations
- Minimizing gas flares (intentional burning of natural gas to the environment) with the goal of eliminating them altogether (Note, often a minimal amount of gas may need to be flared to act as a pilot light as part of the safety system required for some oil production operations)
- Protecting freshwater aquifers and ground water used by humans and wildlife
1.6: Summary and Final Tasks
Summary
In this lesson, we learned about the basics of the modern oil and gas industry. In particular, we learned that naturally occurring hydrocarbons exist in subsurface, porous rock formation called reservoirs. We also learned that these naturally occurring hydrocarbons can be found as liquids (crude oil) or as gases (natural gas).
In addition, we learned about the structure of the oil and gas industry. The modern oil and gas industry is broadly composed of three sectors based on the role that sector plays in delivering petroleum products to consumers. These sectors are:
- the upstream sector: responsible for the discovery and extraction of hydrocarbons from the subsurface reservoirs;
- the mid-stream sector: responsible for transporting oil and natural gas from remote oil and gas fields to refineries and markets; and
- the downstream sector: responsible for the storage, refining, and marketing of refined products.
We also discussed the three disciplines in petroleum engineering and their roles in the industry. These petroleum engineering disciplines are:
- drilling engineering: responsible for planning and drilling all wells in the field;
- production engineering: responsible for monitoring and remediating individual wells to ensure that they are producing or injecting at their optimal potentials; and
- reservoir engineering: responsible for planning and implementing development plans for the oil and gas fields.
In addition, we briefly discussed the career potentials of up and coming petroleum engineers. We learned that petroleum engineers are typically hired into the upstream sector of the industry. In addition, with the aid of the resource triangle, we discussed some of the challenges that future petroleum engineers can expect to take on during their careers in the oil and gas industry.
Finally, we discussed the ethics of the engineering profession, in particular, petroleum and natural gas engineering. We also discussed Environmental Stewardship and its role in crude oil and natural gas extraction.
Final Tasks
Complete all of the Lesson 1 tasks!
You have reached the end of Lesson 1! Double-check the to-do list on the Lesson 1 Overview page [13] to make sure you have completed all of the activities listed there before you begin Lesson 2.
Lesson 2: Origin and Occurrence of Hydrocarbons
2.0: Lesson Overview
Overview
Petroleum and natural gas are found within the pore-spaces of porous rock which forms the crude oil and gas reservoirs. Typically, the oil and gas are found with saline water which may be mobile or immobile. This is in contrast to the popular belief that crude oil is found as “oceans of oil” in vast underground caverns. The pore-space in porous rock is identical to the pore-space found within the sand grains of beach sand. If you were to dig a hole in the sand at the beach and fill it with ocean water, then that water would eventually drain out of the bottom of the hole and migrate through the sand back to the ocean. Oil and gas storage and transport are identical to the storage and transport of ocean water in beach sand. In fact, the physical laws that govern the storage and transport of fluids in porous rock and unconsolidated sand are identical.
Learning Objectives
By the end of this lesson, you should be able to:
- illustrate the types of geologic structures where crude oil and natural gas accumulate and/or exit;
- list the five elements that are required to form a hydrocarbon reservoir;
- describe the rock characteristics that are typically associated with hydrocarbons;
- explain the process by which hydrocarbons pass from source rock to reservoir trap;
- describe the geologic properties that make up a reservoir rock and what properties determine the commercial quality of the reservoir rock;
- identify the four hydrocarbon types that make up crude oil and natural gas;
- apply the Gibbs Phase Rule and explain how it governs the phase behavior of complex hydrocarbon mixtures;
- explain how the local hydrostatic gradient and thermal gradient determine the pressure and temperature of a hydrocarbon reservoir at discovery; and
- summarize how the location of the original pressure and temperature of the reservoir within the phase envelope of the phase diagram determines the type of crude oil or natural gas system that will be produced from the reservoir.
Lesson 2 Checklist
| To Read | Lesson 2: Origin and Occurrence of Hydrocarbons | Click the Basic Earth Geology link below to continue reading the Lesson 2 material |
|---|---|---|
| To Do | Submit the Lesson 2 quiz | Located in the Lesson 2 module in Canvas |
Please refer to the Calendar in Canvas for specific time frames and due dates.
Questions?
If you have questions, please feel free to post them to the Course Q&A Discussion Board in Canvas. While you are there, feel free to post your own responses if you, too, are able to help a classmate.
2.1: Basic Earth Geology
Since the occurrence of crude oil and natural gas are intrinsically associated with reservoir rocks, we must start our discussion of the origin and occurrence of natural hydrocarbons with petroleum geology. Geology is the study of all processes that affect the earth. The earth processes studied by geologists occur at many scales from those at the planetary scale (plate tectonics; interactions between the earth’s core, mantle, and crust; etc.) to those at the grain and pore scale (formation of the cementation that binds sand grains, swelling of clays in pores, etc.). Figure 2.01 shows a schematic diagram (not to scale) of the Earth’s Structure.

Through radiometric dating, the earth is believed to be approximately 4.54 billion years old. As shown in Figure 2.01, it is composed of an inner and outer core, the mantle, and the crust. The earth’s crust is the thin, solid, outer shell of the planet that we live on and interact with on a daily basis. The earth’s crust accounts for approximately 1% of the total volume of the planet.
The solid crust is the upper layer of the lithosphere (the lithosphere is composed of rigid crust and upper portions of the semi-elastic mantle). The earth’s crust can be further divided into the oceanic crust and the continental crust. The oceanic crust is between 3 miles (5 km) and 6 miles (10 km) thick and is overlain by approximately 3 miles of seawater; while the continental crust is between 20 miles (30 km) and 30 miles (50 km) thick. Underlying the oceanic crust and the continental crust is a layer of basalt. Because both the oceanic crust and the continental crust are less dense than the mantle, they both “float” on the mantle.
This floating of the crust on the mantle gives rise to the widely accepted theory of Plate Tectonics. Plate Tectonics is the theory that describes the motion of the continents over the geologic time scale. In this theory, the lithosphere is broken into several major tectonic plates and many smaller plates. The major plates are associated with one of the continents. Slow moving convection currents in the upper mantle are the primary driving mechanisms of plate tectonics; while other mechanisms related to gravity are considered to be secondary driving mechanisms. This is illustrated in Figure 2.02.
In this figure, four tectonic plates are shown along with the convection currents that are driving their drift. The direction of the tectonic drift is shown by the arrows. The separation of tectonic plates is referred to as rifting and is caused by the spreading of two or more convection currents. The mid-Atlantic Ridge is an example of rifting zone. Subduction of tectonic plates, where one plate slides below another plate, results when two or more tectonic plates traveling towards each other collide. The resulting zone is called a subduction zone. A third type of plate boundary, where one plate grinds past another plate, is called a transformational boundary. An example of a transformational boundary is the San Andreas Fault where the Pacific Tectonic Plate is moving across the North American Tectonic Plate.
Due to the friction and built-up stresses in subduction zones and transformational boundaries, these plate boundaries are often associated with volcanism and earthquakes. In fact, the “Ring of Fire” which surrounds the Pacific rim and the North American west coast is caused by the movement of tectonic plates interacting with the Pacific Tectonic Plate.
Rift zones and subduction zones are the only locations where mass transfer from the crust to the mantle (and vice versa) can occur. At a rift zone, fresh rock materials are expelled from the mantle; while at a subduction zone, weathered rock material is returned to the mantle. As we will see, this forms an integral part of the Rock Cycle.
2.2: Rock Types and the Rock Cycle
There are three primary rock types present on the earth: igneous, sedimentary, and metamorphic rocks.
Igneous rocks are rocks formed by the cooling and solidification of molten rock material. As such, igneous rocks are associated with volcanology. There are two types of igneous rocks, intrusive igneous rocks and extrusive igneous rocks. Intrusive igneous rocks crystalize below the earth’s surface, allowing for slow cooling and the development of large crystal structures, while extrusive igneous rocks crystalize on the surface, resulting in rapid cooling and the development of small crystal structures. Examples of intrusive igneous rocks include diorite, granite, and peridotite; while examples of extrusive igneous rocks include basalt, pumice, and tuff.
Sedimentary rocks are rocks formed by the accumulation of sediments. There are three types of sedimentary rocks: clastic sedimentary rocks, chemical sedimentary rocks, and organic sedimentary rocks. Clastic sedimentary rocks are rocks formed by the accumulation of debris that has been mechanically broken by earth processes such as weathering and erosion. Examples of clastic sedimentary rocks include sandstones, siltstones, and shales. Chemical sedimentary rock are rocks that are formed by the precipitation of dissolved materials from high mineral content brines. Examples of chemical sedimentary rocks include rock salt, chert, some limestones, and some dolomites. Finally, organic sedimentary rocks are formed from the accumulation of organic materials (dead plants or animals). Examples of organic sedimentary rocks include coal, some limestones, and some dolomites.
Metamorphic rocks are rocks that started as some other rock type (igneous or sedimentary) but have been substantially altered from their original form by excessive heat, pressure, or exposure to high mineral content brines (or combinations of these three mechanisms). Examples of metamorphic rocks include marble, gneiss, and schist.
As stated in the introduction section of this lesson, crude oil and natural gas reside in the pore-spaces between the grains that make up the rock fabric of the reservoir rock. Consequently, the overwhelming majority of hydrocarbon reservoirs occur in sedimentary rocks where the pore-spaces in the accumulated sediments are sufficiently large to allow for the storage of crude oil and natural gas. While the pore-spaces in metamorphic and igneous rocks are too small to allow for the entry of hydrocarbon molecules, if these rock formations are mechanically fractured by tectonic forces, then the space created by the natural fractures can allow for hydrocarbon storage, and fractured reservoirs in metamorphic and igneous rocks are possible.
It should be emphasized that the formation of rock is not a static process, but is more of a dynamic, cyclical process. In other words: when a rock is formed, it is continually acted upon by earth processes and is subject to change over the geologic time-scale. This process is referred to as the Rock Cycle and is illustrated in Figure 2.03.
2.3: Basic Petroleum Geology
The study of the geological processes that create crude oil and natural gas reservoirs is referred to as Petroleum Geology. In this discussion, we will also need to include brief discussions of related, specialized areas of geologic study including Stratigraphy and Structural Geology. Stratigraphy is the study of the layers (or strata) within rock formations; while Structural Geology is the study of the deformation of rock under tectonic forces. You are probably most familiar with the concepts of stratigraphy and structural geology from road-cuts seen along highways. These road-cuts often show cross-sectional outcrops of layered, deformed rock formations along the road-side. The layering you see is the local geologic stratigraphy; while the deformations you see form the local geologic structure of the rock formations.
Figure 2.04 shows a road-cut along Route 322 approximately 39 miles south of State College, PA. In this photograph, the layering (stratigraphy) and deformation (structure) of the Keefer Formation (Silurian Age) are clearly evident. The “inverted bowl-shaped” feature in this photo is an anticlinal structure, or simply an anticline. Anticlines statistically form the most common crude oil and natural gas reservoirs. We will discuss this in more detail when we discuss Reservoir Traps later in this lesson.
As we have already discussed, hydrocarbon reservoirs are typically associated with sedimentary rock formations. Over geologic time, weathered and eroded rock materials are carried downstream from elevated regions to lower regions in rivers and streams to oceans, seas, or lakes. At the point in the rivers, oceans, seas, or lakes where the energy in the water can no longer suspend or transport the rock material, it begins to settle in the water and is deposited onto the bottom of the water body. This is called the depositional process. During the depositional process, the environment can change over the geologic time scale: mountain tops and hilltops erode, sea-levels rise or lower, etc. With these changes, the types of sediments that are deposited change and the locations where they are deposited also change. Two commonalities that exist during the depositional process, even over the geologic time scale, are (1) the sediments and, consequently, the sedentary rocks that are lower in the stratigraphic column were deposited earlier than sediments higher in the stratigraphic column and (2) the layers of sediment are initially deposited horizontally. From this discussion, we can see that sediments lower in the stratigraphic column must be older than those higher in the stratigraphic column.
Note, a stratigraphic column is a written, pictorial, or schematic record of the local rock strata showing the order of the rock deposition (older rocks at the bottom and younger rocks at the top), along with notes concerning the age of the rocks, occurrence of any fossils, any rocks which may be absent from the local geological record due to erosion, or any notes of use to a geologist. One example of a stratigraphic column that you may be familiar with is The Obelisk on the University Park Campus of Penn State. The Obelisk is a physical column constructed of quarried building materials from Pennsylvania with the older rocks placed at the base of the column and the younger rocks placed at the top of the column. Consequently, it forms a true stratigraphic column of the building stones of Pennsylvania. A photograph of The Obelisk is shown in Figure 2.05.
From this discussion, we can also see that in their original, natural state, sedimentary rocks are horizontal. Any deformation (folding, uplifting, tilting, faulting, etc.) in sedimentary rock formations is caused by tectonic forces acting on the rock after deposition and solidification.
There are five geological requirements for the formation of a conventional hydrocarbon reservoir:
- Source Rock
- Migration Path
- Cap Rock
- Reservoir Rock
- Trap
These geological requirements are illustrated in Figure 2.06. It needs to be emphasized that although this figure consists of solid colored bands, these bands represent either porous or non-porous rocks. In the following discussions, all of the action concerning this figure is occurring in the pore-spaces of porous rock.
In this figure, the Source Rock is represented by the light grey layer. This is the rock in which the original organic material is converted into hydrocarbons. We will discuss this process later in this lesson. As we can see from this figure, the hydrocarbons do not necessarily originate in the hydrocarbon reservoir itself but are generated away from the reservoir in rocks that are conducive to hydrocarbon generation. As we will discuss later, these source rocks are typically organic-rich shales, siltstones, or coals.
Since the hydrocarbons are generated away from the reservoir, there must be a pathway for the hydrocarbons to migrate from the source to the reservoir. This pathway is the Migration Path in the hydrocarbon system. In the example shown in Figure 2.06, the migration path is a water-filled rock layer (aquifer) that is in communication with both the source rock the hydrocarbon bearing reservoir. This aquifer is shown as the blue layer in Figure 2.06.
In Figure 2.06, the solid green arrows represent the primary migration of the hydrocarbons, while the dashed green arrows represent the secondary migration of the hydrocarbons. Primary migration refers to the initial expulsion of the hydrocarbons from the source rock, while secondary migration refers to the remainder of migration to the reservoir.

As shown in this figure, all fluid migration is upward. This is because the main driving mechanism in hydrocarbon migration is buoyancy, which occurs because the oil and gas are less dense (lighter) than the resident water. In order to prevent this buoyant flow from occurring all of the way to the surface, a vertical flow barrier, or Cap Rock, is required along the migration path and at the reservoir itself. A cap rock is simply an overlying rock layer that is impermeable to flow. Permeability is a property of the rock that is a measure of the ease in which fluids can flow through a porous medium (in our case, a rock formation). In Figure 2.06, the cap rock is depicted by the black layer.
The fourth requirement for a hydrocarbon accumulation is the presence of a Reservoir Rock. In the example shown in Figure 2.06, the reservoir rock is the same rock formation as the migration path. As stated earlier, the most common reservoir rocks are sedimentary rocks; however, naturally fractured igneous and metamorphic rocks can also form hydrocarbon reservoirs. The two requirements for a commercial crude oil or natural gas reservoir are high porosity and high permeability. As discussed earlier, oil and natural gas exist in the pore-space between the grains of the sedimentary rocks. The porosity of a rock is defined as the fraction of the rock’s bulk (total) volume occupied by the pores. For example, a cubic foot (1 ft3) of rock with 15 percent porosity will contain 0.15 ft3 of pore space. Consequently, a rock formation with a higher porosity implies greater storage capacity than a rock formation with a lower porosity. This, in turn, results in the possibility of greater quantities of oil and gas stored in the more porous rock.
As discussed earlier, permeability is defined as the ease in which fluids flow through porous media. A high permeability formation implies greater oil and gas production rates and more economically attractive production wells.
The last component of a hydrocarbon system is the Trap. A trap or trapping mechanism is a change in the stratigraphy or a structural deformation that is capable of stopping the migration process and keeping the oil and gas in place over geologic time. In the example in Figure 2.06, the trap is an anticline like that shown in the photograph in Figure 2.04.
Statistically, anticlines are the most common traps; however, they are not the only types of hydrocarbon traps. Crude oil and natural gas traps can be categorized as Stratigraphic Traps or Structural Traps. As the names imply, stratigraphic traps are related to the layering of the rock strata; while structural traps are related to the structural deformations of the rock formations.
Examples of stratigraphic hydrocarbon traps are shown in Figure 2.07. Figure 2.07 shows (a) a “pinch-out” trap and (b) an unconformity trap. In these figures, the yellow layers represent reservoir quality rock (Reservoir Rock); while the green areas represent an oil accumulation in the reservoir trap.

A pinchout trap, Figure 2.07a, is formed due to the relative rise and fall of a water body in relation to the local land mass. (Note: a relative rise or fall may be due to either a true rise or fall of the sea level, or a subsidence or uplift of the land mass.) In this figure, the crude oil reservoir is represented by the green area encased in the black, impermeable layer. As mentioned earlier in this lesson, the size and weight of the sediments that form sedimentary rocks are deposited in water are dependent on the energy of the water suspending the particles. Heavier, coarser materials can only be suspended in high energy environments near the shore where wave and tidal action keep these materials mixed with the water. These materials are deposited as sediments at the point in the depositional environment where the wave and tidal energy can no longer support them. On the other hand, lighter, finer sediments can be suspended in low energy environments away from the shore in more calm waters and, consequently, are deposited further from the shoreline. As the relative position of the sea level changes over the geologic time scale, the positions of the coarser and finer sediments change. The coarser materials with the larger pore spaces between the sediment grains often make good quality rock, while the finer materials, particularly clays and silts, with smaller pore spaces make good impermeable seals (cap rocks). Under the proper sequence of events, as the geographical locations of the sediments change over the geologic time scale, the changes in the size of the sediments can create pinchout, or stratigraphic trap.
Figure 2.07b shows an unconformity trap. A geological unconformity is a boundary between two rock sequences of different ages that are missing some transitory rock sequences of intermediate ages - in other words, some rock strata are missing from the local geological record. This gap in the geological record is caused by a past erosional period.
The depositional history of an unconformity trap is slightly more complicated than that of a pinchout trap. In this trap system, an early depositional period caused sedimentary rocks to be deposited horizontally. These rocks were then tilted due to local tectonic forces. These form the lower tilted layers in Figure 2.07b. The higher, uplifted portions of the tilted layers were then eroded over geological time. The orange wavy line represents an unconformity surface where rocks are missing from the geological record. Geologists recognize these unconformity surfaces when they see rocks of one age sitting on top of rocks of a different age with no intermediary age rocks between them; while paleontologists recognize unconformities by rocks containing fossils from one age sitting directly on top of rocks containing fossils from a different, much older age. After subsidence, a second depositional period occurs where additional sedimentary rocks are again deposited horizontally over the erosional surface. In order for an unconformity trap to develop, the first layer deposited during the second depositional period must be an impermeable rock which can act as the cap rock for the reservoir. After the second depositional period, the trap can be charged with crude oil to form the oil reservoir - the green area of the figure. (Note that the horizontal yellow layer representing good quality reservoir rock above the unconformity surface, does not contain crude oil or natural gas. This is because it is missing a trapping mechanism at this location.)
These histories illustrate the critical nature of the timing in the development of hydrocarbon reservoirs. For a hydrocarbon reservoir to develop, all five elements of the reservoir system must be in place prior to the formation and migration of the hydrocarbons. If one element is missing from the system, then a crude oil or natural gas reservoir cannot develop.
The second major category of hydrocarbon reservoirs is structural traps. Structural traps, illustrated in Figure 2.08, are related to mechanical deformations and failures of the reservoir rock. Figure 2.08a shows an anticlinal structure, or anticline. As stated earlier, the anticline is statistically the most common reservoir trap. The reason for this is very simple. An anticlinal trap simply requires that the reservoir rock and cap rock be folded in a manner that can trap the lighter hydrocarbons. Figure 2.04 shows the Arch Rock anticline near State College, PA.
Figure 2.08b shows a fault trap. A fault trap is created when a rock formation undergoes mechanical failure during an earthquake and the resulting fault causes a porous and permeable rock formation (reservoir rock) to be positioned adjacent to an impermeable rock formation. Thus, closure to the trap is formed by the cross-fault impermeable layer.
Figure 2.08c shows traps along a salt dome. These traps are common in areas where salt formations exist, such as in the Gulf of Mexico. Since large volumes of salt behave in a plastic manner over geologic time, the weight of the overburden creates great pressures within the salt causing it to flow through any local weak spots in the overburden. These salt intrusions can create hydrocarbon traps above and to the flanks of the intrusion as depicted in Figure 2.08c.

2.4: Origins of Oil and Natural Gas
To this point, we have discussed the elements required for the formation of a hydrocarbon reservoir. We have also discussed the timing and histories of the formation of the reservoir traps. We have also mentioned that all of the elements of the hydrocarbon reservoir must be in place prior to the formation and migration of the hydrocarbons. We are now able to discuss the actual formation of the hydrocarbons themselves.
Petroleum and natural gas are naturally occurring substances composed of hydrocarbon molecules (molecules made up of hydrogen and carbon atoms) and, possibly, non-organic contaminants, such as CO2, H2S, N2, and O2.
The most widely accepted theory of the origin of petroleum and natural gas is the Organic Origin Theory which states that these fluids are generated from the decay of prehistoric plants and animals under the influence of the excessive pressures and temperatures that exist in the earth’s subsurface. Research indicates that petroleum and natural gas originated from zooplankton (single-celled plants found drifting freely in fresh or brackish water) and algae. During their lifetimes, these organisms create energy from photosynthesis to carry out their life processes, and it is this energy that we use today (thus the term, “fossil fuels”). Contrary to the popular myth, petroleum and natural gas do not originate from decomposed dinosaurs.
Over the geologic time scale, these free-floating zooplankton and algae die, settle to the ocean-, sea-, lake‑, river‑, or swamp-bottom, and accumulate as sediment. This process occurs simultaneously with the geological processes (erosion, transportation, and deposition) acting on the sand, silt, and clay sediments that form sedimentary rocks. As the organic material and rock materials accumulate on the sea bottom, the materials at the top of the accumulation exert increased weight (pressure) on the materials at the bottom of the accumulation. As this depositional process continues and the accumulation becomes thicker, the impact of the earth’s geothermal gradient also begins to act on the organic materials. At elevated pressures and temperatures, the decaying organic materials are transformed into a dark waxy material called kerogen. Kerogen is an intermediary stage in the development of petroleum. The process of converting the original organic material into kerogen is called the Catagenesis Process. The formation of kerogen requires that the rock containing the original organic material be impermeable. This requirement is essential because as kerogens are formed, they must remain trapped within the pore-spaces of the rock and cannot be allowed to escape to other rock formations or to the environment. As we have already discussed, the rock formation in which the original organic materials are converted to kerogen, and eventually petroleum, are called source rocks for the hydrocarbons. Typically, fine-grained, clay-rich sedimentary rocks, such as shales, are the most common source rocks for hydrocarbon basins because they satisfy two of the requirements for kerogen generation; they (1) are sedimentary rocks and (2) contain adequately low permeabilities.
During the catagenesis process, the kerogen is “cooked” in the high-temperature environment, and the long-chain kerogen molecules are “cracked” into shorter-chained hydrocarbon molecules. It may take several million years for the deposition process to bury the original organic materials and the source rock to achieve the appropriate temperatures (> 250 - 300 ºF) for kerogen generation and another several million years to generate commercial quantities of oil and gas. There is a specific temperature range, referred to as the “oil window,” in which oil is formed. At temperatures below the oil window, the catagenesis process cannot occur; while at higher temperatures the “cooking” and “cracking” processes are stronger and very short-chain natural gas molecules are generated (thermogenic gas).
A second, less accepted theory for the origin of hydrocarbons is the Inorganic or Abiogenic Theory. In this theory, hydrogen and carbon from inorganic sources are fused at the elevated pressures and temperatures in the earth’s subsurface and are converted to hydrocarbons. While the presence of inorganically sourced hydrocarbons cannot be discounted, there is abundant evidence that the vast majority of crude oil and natural gas have an organic origin.
2.5: Hydrocarbon Types
Crude oil is a complex mixture of several types of hydrocarbon molecules along with inorganic impurities. These hydrocarbon molecules are:
- Paraffinic (or alkane series) hydrocarbons
- Naphthenic (or saturated cyclic) hydrocarbons
- Aromatic (or cyclic) hydrocarbons
- Asphaltene hydrocarbons
Sometimes we refer to a particular crude oil as a paraffinic crude oil or as an aromatic crude oil. While there may be several thousand different hydrocarbon molecules in a given crude oil, these descriptions simply refer to the dominant hydrocarbon type in the mixture. All naturally occurring crude oils will typically contain molecules of each type.
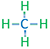
Paraffinic, or alkane series, hydrocarbons are shown in Table 2.01. These hydrocarbons are typically studied in introductory courses in Organic Chemistry. Alkane series hydrocarbons are composed of only hydrogen and carbon atoms attached with single bonds. They are characterized by the following formula for the number of hydrocarbon atoms present in the molecule:
In this formula, NH is the number of hydrogen atoms, while NC is the number of carbon atoms in the hydrocarbon molecule.
Normal alkanes are the chain molecules depicted the first four examples in Table 2.01. Once the number of carbon atoms reaches four (butanes) different permutations of an alkane molecule can exist that still honor Equation 2.01 but do not form chain molecules. These permutations are called isomers with the number of possible permutations (and number of isomers) increasing as the number of carbon atoms, NC, increases. An example of the difference between a normal and isomeric alkane is shown in Table 2.01 for n-butane and i-butane. Due to the slight discrepancies in the molecular structures, normal alkanes and isomeric alkanes have slightly different physical and chemical properties, such as, boiling points, melting points, etc.
| Compound | Formula | 2D Representation | 3D Representation |
|---|---|---|---|
| Methane | CH4 |
 |
 |
| Ethane | C2H6 |
 |
 |
| Propane | C3H8 |
 |
 |
| N-Butane Normal Butane |
C4H10 |
 |
 |
| I-Butane Isomeric Butane |
C4H10 |
 |
 |
As the number of carbon atoms increases, the molecular weight of the molecule increases. The lower molecular weight alkanes, methane and ethane, are the most common hydrocarbon components in natural gas; however, intermediate molecular weight alkanes up to the butanes may also be present in natural gases. In addition to these hydrocarbon components, some inorganic impurities, such as CO2, H2S, N2, and O2 may also be present in natural gases.
Crude oils from Pennsylvania are generally classified as Paraffinic Crude Oils (“Pennsylvania Grade Crude Oil” was at one time a phrase used to describe high quality crude oils.). As a solid, the alkanes form a waxy substance, paraffin, which is the main component of such products as paraffin candles.
The second category of hydrocarbon molecules found in crude oils are naphthenic (or saturated cyclic) hydrocarbons. Like the alkanes, these hydrocarbons are composed of hydrogen and carbon atoms attached with single bonds; however, they differ from the alkanes in that they do not form chain structures but form cyclic (ring) structures. Examples of naphthenic hydrocarbons are shown in Table 2.02.
| Compound | Formula | 2D Representation |
|---|---|---|
| Cyclopropane | C3H6 |
 |
| Cyclobutane | C4H8 |
 |
| Cyclopentane | C5H10 |
 |
The third category of hydrocarbon molecules found in crude oils are the aromatic (or cyclic) hydrocarbons. These hydrocarbons are composed of hydrogen and carbon atoms that form cyclic structures but contain dual bonds between alternating carbon atoms. The simplest aromatic hydrocarbon is benzene with a single ring structure; while more complex aromatic hydrocarbons are typically formed with multi-ring structures. As the name implies, aromatic hydrocarbons, such as benzene, are associated with a sweet smell. Examples of aromatic hydrocarbons are shown in Table 2.03.
The last category of hydrocarbon molecules found in crude oils are the asphaltene hydrocarbons. These hydrocarbons are large, high molecular weight molecules which may also contain some atoms other than hydrogen and carbon atoms, such as, sulfur, oxygen, or nitrogen atoms. Asphaltenes typically result in the residue from the refining process and are the principal components of asphalt (road paving), tar, and bitumen products.
The mixture of these hydrocarbon molecules can have several consequences on oil and gas production, transport, and refining. These include:
- The mixture of hydrocarbon molecules gives the bulk fluids (oil and gas phases) the properties which dictate the ease or difficulty in which they flow through the reservoir towards production wells and through production equipment
- The nature of any solids which may precipitate from the bulk fluids onto rock grains, wellbore, or surface equipment during production causing operational problems requiring different solutions:
- Paraffinic crude oils may deposit waxy solids onto the reservoir rock, well completion, or production tubing causing restrictions to flow requiring a remediation treatment, such as hot kerosene injection into the well.
- Asphaltic crude oils may deposit hydrocarbon resins onto the reservoir rock, well completion, or production tubing causing restrictions to flow requiring a remediation treatment, such as solvent injection into the well.
- Local field treatment of the crude oil to upgrade it to the required specifications for the pipelines and refineries where the crude oil will eventually flow
- The products that can be refined from the crude oils once they reach the refineries: lubricating oils, heating oils, car or aviation fuels, asphalt and tar products, etc.
| Compound | Formula | 2D Representation |
|---|---|---|
| Benzene | C6H6 |
 |
| Napthalene | C10H8 |
 |
The definitive methods for determining the different components in crude oil are with laboratory measurements, such as gas chromatography. Often, however, less rigorous methods may be useful for quick, on-site evaluations or for numerical (computer) calculations where the crude oil type is characterized with a single parameter. In the oil and gas industry, one common measure of the dominant character of the crude oil (paraffinic, naphthenic, and aromatic) is the Watson Characterization Factor[1] (or a generalization suggested by Whitson[2]). The original form of the Watson Characterization Factor, KW, is:
Where:
KW is Watson Characterization Factor, oR1/3
Tb is the mean average boiling point of the mixture, oR
ϒo is the specific gravity of the mixture, dimensionless
This equation requires that the boiling point, Tb, for the mixture of interest is known. In many cases, Tb is unknown or difficult to measure. For these cases, Whitson correlated the Watson Characterization Factor with the more commonly known molecular weight:
Where:
KW is Watson Characterization Factor, oR1/3
Mo is the molecular weight of the mixture, lbm/lbm-mol
ϒo is the specific gravity of the mixture, dimensionless
The guidelines for the use of the Watson Characterization Factor are:
- KW ≥ 12.5 indicates a paraffinic crude oil
- 12.5 > KW ≥ 10 indicates a crude oil containing naphthenic or aromatic components
- KW < 10 indicates a highly aromatic crude oil
Table 2.04 shows the values of the Watson Characterization Factor for substances of known hydrocarbon type (paraffinic, naphthenic, and aromatic).
| Hydrocarbon Series |
Substance | Formula | Tb (oR) |
Mo (lbm/lbm-mol) |
Υo |
Kw(oR1/3) Eq. 2.02a |
Kw(oR1/3) Eq. 2.02b |
|---|---|---|---|---|---|---|---|
| Paraffin | n-Hexane | C6H4 | 615.4 | 86.178 | 0.6640 | 12.8 | 12.7 |
| 2-Methylpentane (A) | C6H14 | 600.1 | 86.178 | 0.6759 | 12.8 | 12.8 | |
| n-Heptane | C7H16 | 668.8 | 100.205 | 0.6882 | 12.7 | 12.6 | |
| Napthene | Cyclohexane | C6H12 | 637.0 | 84.162 | 0.7834 | 11.0 | 11.0 |
| Methylcyclohexane | C7H14 | 673.4 | 98.189 | 0.7740 | 11.3 | 11.4 | |
| Aromatic | Benzene | C6H6 | 635.8 | 78.114 | 0.8844 | 9.7 | 9.8 |
| Toluene | C7H8 | 690.8 | 92.141 | 0.8718 | 10.1 | 10.2 |
(A) One of the isomers is Hexane
2.6: Types of Hydrocarbon Reservoirs
To this point in the lesson, we have discussed the origins of the reservoir rocks and traps that formed over the geologic time scale which result in modern oil and gas reservoirs. We have also discussed the origins of the hydrocarbons that reside in pore spaces of these reservoirs. We can now discuss the types of reservoirs and reservoir systems that are currently of commercial interest to the oil and gas industry. To aid in this discussion, we must first introduce the concept of the Phase Envelope (or, Phase Diagram, or Pressure-Temperature Diagram, or P-T Diagram) for single-component (pure) and multi-component (mixture) systems.
2.7: The Gibbs Phase Rule
The Gibbs Phase Rule relates the degrees of freedom in a system to the number of components and number of phases in a system. The Gibbs Phase Rule is:
Where:
F the number of degrees of freedom in the system, integer
C is the number of components in the system, integer
P is the number of phases in the system, integer
The use of the Gibbs Phase Rule is best illustrated with examples; however, to do this we must first discuss some fundamental thermodynamic concepts. The phrase “degrees of freedom” refers to the maximum number of independent thermodynamic variables (pressure, temperature, and intensive variables) that you can vary simultaneously within a system at equilibrium before you are forced to specify one or more of the remaining variables (or disturb the equilibrium of the system). By “intensive variables”, we are referring to variables that are independent of the size of the system. For example, phase density in a system is an intensive variable because you can halve the size of the system, and the phase density will remain the same. On the other hand, the mass of a system is an extensive property because if you halve the size of the system, then you halve the mass in the system. A component refers an individual chemical element that exists in the system (in our case, a molecular species: methane, ethane, cyclopentane, benzene, CO2, H2O, etc.). Finally, a phase is a physical state of matter with homogenous (uniform) composition, physical properties, and chemical properties. In petroleum and natural gas engineering, we typically deal with systems containing four phases: a gaseous hydrocarbon phase (natural gas), a liquid hydrocarbon phase (crude oil), a liquid aqueous phase (water or brine), and a solid rock phase. There are times when we deal with systems containing more phases (such a solid hydrocarbon phase or multiple hydrocarbon liquid phases), but the circumstances when this occurs are beyond the scope of this class.
For a single-component system, we have C = 1, and Gibbs Phase Rule becomes:
If we were to plot the phase state (number and types of phases) on a pressure-temperature plot for this single-component system, then we would obtain a plot like that shown in Figure 2.09. This figure is also referred to as a Phase Diagram or a P-T Diagram. In this Phase Diagram, the grey region represents all of the pressure-temperature combinations that result in the solid form of our single component, the green region represents the pressure and temperature combinations that result in the liquid form of our single component, the red region represents the pressure and temperature combinations that result in the gaseous form of our single component, and the multi-colored region represents the super critical form of our single component. Also posted on this Phase Diagram are two points, the triple point and the critical point.
Getting back to the single component version of the Gibbs Phase Rule, Equation 2.04, we can start to clarify some of the concepts that we have already discussed with some examples. If we consider the single-phase regions in Figure 2.09 (P = 1 in Equation 2.04), then from Equation 2.04, we have 2 degrees of freedom (F = 2). This implies that we can independently vary Pressure and Temperature within the Phase Envelope (colored regions) and not change the phase state of the system. In other words, two degrees of freedom represent two-dimensional regions (areas) on the Phase Diagram in which a single phase exists.
Now, let’s consider the occurrence of two phases coexisting simultaneously (P = 2) in equilibrium. From Equation 2.04 with P = 2, we have one degree of freedom (F = 1). In Figure 2.09, we have two coexisting phases along the borders of the phase envelopes. For example, the line bordering the Solid and Liquid Phases represents the pressure-temperature conditions where the solid form of our single component system can coexist with the liquid form of our single component at equilibrium (think of polar caps sitting on water near the earth’s poles). For two phases to coexist in equilibrium, if we were to change one variable, say temperature, then we would be forced to change pressure in a manner that it remained on the border line between the two single-phase regions. In other words, one degree of freedom represents the one-dimensional, curvilinear lines which act as borders between the single-phase regions. If we change one variable on one of these border lines, then we are forced to change the other variable to remain on the border line.

Finally, we can consider the coexistence of three phases (P = 3 in Equation 2-4) in a system at equilibrium. From Equation 2.04 with P = 3, we have F = 0, or no degrees of freedom. This implies that at the point where three phases coexist (the Triple Point in Figure 2.09), we cannot change either pressure or temperature and retain a three-phase system in equilibrium of the single-component (pure) system. The Triple Point is a property of the component that we are considering. Thus, zero degrees of freedom refers to a 0-Dimensional point (the Triple Point)
In Figure 2.09, the Critical Point is also plotted. The Critical Point, defined by the critical pressure, Pc, and the critical temperature, Tc: (Pc, Tc) is the point in the system that defines the onset of the super critical state. Super critical fluids are fluids in which the gaseous phase becomes indistinguishable from the liquid phase (the phase densities become equal).
Consider a pressure-temperature pair in the single-phase gas region with a temperature somewhere between the temperature at the triple point and the critical temperature, Tc, such as Point A in Figure 2.10. If we were to increase the pressure of this single-phase gas (Path A-A’), then we would see a distinct and abrupt change in the phase state of the fluid as we crossed into the single-phase liquid region. This is because the densities of the gaseous phase and the liquid phase are different. Now, if we were to do the same experiment starting at a temperature greater the critical temperature, Tc, such as Point B, then as we increased the pressure on the single-phase gas (Path B-B’) and entered the Super Critical Fluid region, there would be no abrupt phase change.
We could also perform a third experiment where we started at the original point, Point A, and followed the pressure-temperature path Path A-B-B’-A’ into the single-phase liquid region to arrive at Point A’. In this last experiment, we would arrive at the same point, Point A’, as in the first experiment, but without any abrupt phase change. The system properties would change smoothly and continuously during the entire experiment.

For multi-component systems like real crude oil – natural gas systems, the Pressure-Temperature Diagram is much more complex. This is because a real crude oil – natural gas system may contain tens or hundreds of thousands of components. For Multi-Component Systems, the P-T Diagram looks like that in Figure 2.11. A Phase Diagram, such as that shown in this figure, typically is measured in the laboratory but can also be generated mathematically with sophisticated models, such as, Cubic Equation of State Equations (multi-component extensions to van der Waal’s Equation).

In this figure, the region between the green curve and the red curve is the two-phase envelope; while the region outside of the two-phase envelope is the single-phase region. Single-phase liquids exist to the left (lower temperatures) and above (higher pressures) the bubble-point locus (green curve); while single-phase gases exist to the right (higher temperatures) of the dew-point locus (red curve).
The green curve in this figure represents the Bubble-Point Locus of this multi-component system; the red curve represents the Dew Point Locus of the system, and the dashed lines in the two-phase region represents the quality lines of the system (lines of constant volume-fraction of the liquid phase). The bubble-point, defined by a bubble-point pressure, Pb and a bubble-point temperature, Tb, is the point on a pressure-temperature path (originating in the single-phase liquid region) where the path enters the two-phase region (crosses the green curve in Figure 2.11). The name “bubble-point” comes from the fact that this is the point where the first bubble of gas evolved from a liquid as it enters the two-phase region. For example, Point A in Figure 2.11 lies in the single-phase liquid region. As the pressure is reduced at a constant temperature (isothermal conditions), it follows the Path A-A’. The point where Path A-A’ enters the two-phase region (crosses the green, bubble-point locus) represents the bubble-point pressure for this temperature. This is the point where the first bubble of gas is formed in the system. The pressure reduction is continued until it terminates at Point A’. Point A’ lies on the 0.9 quality line, implying that at this point, the system is composed of two-phases with the liquid phase occupying 90 percent of the volume.
On the other hand, the dew-point, defined by the dew-point pressure and dew-point temperature is the point on a pressure-temperature path (originating in the single-phase gas region) enters the two-phase region. The name dew-point refers to the point where the first liquid drop condenses from the gaseous phase. For example, Point B in Figure 2.11 lies in the single-phase gas region and enters the two-phase region when the pressure is reduced under isothermal conditions (Path B-B’). The dew point pressure for this temperature then is the pressure where Path B-B’ crosses the red dew-point locus. If the isothermal pressure reduction is stopped at Point B', then the system at equilibrium will contain two phases with the liquid phase occupying 10 percent of the system volume.
Finally, the pressure, Pmax in Figure 2.11 is the cricondenbar (the maximum pressure in which two phases can coexist); while the temperature, Tmax is the cricondentherm (the maximum temperature in which two phases can coexist).
With these preliminary concepts, we can now continue with our discussion on the types of hydrocarbon reservoirs encountered in the oil and gas industry.
2.8: Undersaturated Black Oil (Low Shrinkage Oil) Reservoirs
Undersaturated black oils, sometimes referred to as “low shrinkage oils,” are single-phase liquid systems that reside in reservoirs with an original temperature that is significantly lower than critical temperature, TC. The phase diagram for an undersaturated black oil is shown in Figure 2.12.
In this figure, the reservoir temperature, TR, and reservoir pressure, pR, at the time of discovery are determined by the earth’s local temperature gradient and hydrostatic pressure gradient, respectively. The phase diagram for the crude oil is determined by the composition of the crude oil. As shown in this figure, the original reservoir temperature and pressure lie in the single-phase liquid region of the phase diagram at a temperature lower than the critical temperature.
The term “undersaturated” implies that the crude oil has the capacity to dissolve additional gaseous components and remain in the single-phase region. For example, if we change the composition of the system by adding more lower molecular weight components (e.g., methane and ethane), then the phase envelope would expand with the bubble-point locus beginning to shift towards the Point (TR, pR). In this example, we could continue to add gaseous components to the system until the bubble-point locus has shifted all of the way to the Point (TR, pR). At this point, with Point (TR, pR) lying on the bubble-point locus, we would call the fluid a bubble-point fluid. This is the point where the system would be unable to accept additional gaseous components and still remain a single-phase liquid, i.e., a single-phase crude oil. We will discuss the significance of the term “low shrinkage” when we discuss “high shrinkage” volatile oils.
The production of oil and gas is an isothermal process. We typically deplete the reservoir pressure by removing fluids from the system. Even in the cases where we inject fluids at different temperatures into the reservoir, such as with steam injection, the volume of fluids that we inject are so small compared to the size of the reservoir and the over- and under-burdens that, at most, we cause a local change in the temperature at the point of injection and have no significant impact on the temperature of the system. For isothermal processes, the pressure-temperature path of the fluids inside the reservoir is a vertical line at a fixed temperature. This is represented in Figure 2.12 (A) as the solid black arrow going from Point (TR, pR) to Point (TR, pA).

Figure 2.12 (B) shows the undersaturated black oil in an anticlinal trap at the time of discovery, that is, at the original reservoir temperature, TR, and pressure, pR. This figure depicts a single-phase liquid hydrocarbon (crude oil) system. As we produce reservoir fluids, single-phase oil (and the dissolved natural gas components) and possibly water, the pressure in the reservoir depletes. This is the solid arrow from Point (TR, pR) to Point (TR, pA). At some point in time, the reservoir pressure drops below the bubble-point pressure, and we enter the two-phase region in the phase diagram. At this point in time, a second, free gas phase evolves in the reservoir. This occurs when the path of the reservoir fluids crosses the green, bubble-point locus.
As we continue production, we now produce crude oil (and the gas dissolved in it), free natural gas, and, possibly, water. At some point during the depletion process, the natural pressure in the reservoir becomes so low that it can no longer overcome the weight of the fluids in the wells and lift these fluids to the surface at commercial rates. At that point in time, we may be able to install some form of artificial lift (e.g., pumps) to help the natural reservoir pressure lift the reservoir fluids, but that is only a temporary solution, and eventually we will be forced to abandon the reservoir. The pressure at which we abandon the reservoir is called the “abandonment pressure,” pA.
Figure 2.12 (C) shows the same reservoir at abandonment conditions after the free gas phase has developed. Since gas is lighter than oil, it will migrate to the top of the reservoir and accumulate there. When gas comes out of solution due to pressure depletion and accumulates at the top of a reservoir, we refer to the resulting accumulation as a “secondary gas cap.”
Please note that we may run into some situations in which the abandonment pressure occurs before we drop below the bubble-point pressure. In these cases, the path of the reservoir fluids would remain in the single-phase liquid region, and a free gas phase would never develop in the reservoir.
Also depicted in Figure 2.12 (A) is the dashed arrow from Point (TR, pR) to Point (TS, pS). This is the path that the reservoir fluids travel in the well and through the surface facilities. Point (TS, pS) refers to the separator conditions. The separators are field equipment, typically designed by facilities engineers, that are used to separate the produced fluids. Normally, produced oil has a higher commercial value to the oil and gas company than produced natural gas, so typically the facilities engineers design the separators to optimize the volume of liquid at the surface. In other words, the faculties engineers will design the separator conditions TS and pS to lie on the quality line of the phase diagram with the maximum feasible volume percent liquid.
2.9: Saturated Black Oil (Low Shrinkage Oil) Reservoirs
Saturated black oils are oils which are fully saturated with natural gas components (e.g., methane and ethane). This implies that the original reservoir temperature and pressure are in the two-phase region of the phase diagram at the time that the reservoir is discovered. This is shown in Figure 2.13.

Figure 2.13 (B) shows a saturated black oil in an anticlinal trap. In this figure, we can see that a gas cap overlies the oil at discovery. Since this gas accumulation was present at the original temperature and pressure conditions, we refer to this gas accumulation as a “primary gas cap.” Figure 2.13 (C) shows the state of the reservoir at abandonment conditions. As shown in this figure, at the lower pressure condition, the gas cap size has expanded.
2.10: Undersaturated Volatile Oil (High Shrinkage Oil) Reservoirs
Undersaturated volatile oil reservoirs are single-phase oil systems that reside in reservoirs with an original temperature relatively close to the critical point (relative compared to low shrinkage oils). As with the undersaturated black oils, the term undersaturated implies that the original reservoir temperature and pressure lies in the single-phase liquid region of the phase diagram. Such a system is shown in Figure 2.14.

We are now in a position to discuss the terms “low shrinkage oil” and “high shrinkage oil” as they pertain to the oil and gas industry. The blue bars on Figure 2.14 (A) represent equal pressure drops below the bubble-point pressure (these bars are of equal length). We can see from this figure that due to the convergent nature of the quality lines (dashed lines) near the critical point, equal pressure drops result in different volume percentages of the liquid phase in the two-phase region. The pressure drop represented by the blue bar further from the critical point results in a two-phase system with 90 percent of the volume occupied by the liquid phase; while the blue bar closer to the critical point results in a two-phase system with 80 percent of the volume occupied by the liquid phase. Thus, the volume of the liquid phase shrinks more in a system that is closer to the critical point for similar pressure drops. Since the liquid phase occupies less volume for a volatile, high shrinkage oil for comparable pressure drops, at abandonment the secondary gas cap will occupy a larger volume.
The definition of a “volatile fluid” is a fluid that easily evaporates or vaporizes. This definition gives rise to the name “volatile oils.” These systems develop larger gas phase volumes for comparable pressure drops when entering the two-phase region of the phase envelope.
2.11: Gas Condensate Reservoirs
Gas condensate reservoirs are gas systems that reside in reservoirs with the original temperatures lying between the critical temperature, TC, and the cricondentherm (Tmax in Figure 2.11). If the original reservoir pressure is greater than the dew-point pressure, then a single-phase gas system will occur in the reservoir as in Figure 2.15.
In this figure, the reservoir is initially a single-phase gas, but as we deplete the pressure due to gas production the pressure-temperature path of the system enters the two-phase region of the phase envelope and liquid hydrocarbons condense from the gas in the reservoir (thus the name gas condensate reservoir.)

We are actually very familiar with this process in our everyday lives. Think of a four-component mixture of oxygen, carbon-dioxide, nitrogen, and water vapor (a mixture of air) and its phase envelope. If we started at a point in the single-phase gas region with a pressure below the cricondenbar (pmax in Figure 2.11) and reduced the temperature under constant pressure conditions (isobaric conditions), then we would cross the dew point locus of the phase envelope. This would be the pressure and temperature where we would see the first dew forming on plants and the first water condensation forming on glass and metal. If we were to continue reducing the temperature, then the percent volume of liquid (water) would increase and it would begin to rain. What is happening in this simple example is that the heaviest component in our system (water vapor) is condensing out of the gas phase (air mixture) and forming a second phase (liquid water) in the two-phase region.
This is essentially what is occurring in the reservoir of a gas condensate system but under isothermal conditions. As we pass through the dew point pressure, the heaviest hydrocarbon components in the system begin to drop out and form a second, liquid hydrocarbon phase in the two-phase region of the phase envelope inside the reservoir.
There is one interesting characteristic of gas condensate reservoirs that is worth further discussing and that is the retrograde behavior of these systems. This is illustrated in Figure 2.16. In this figure, if we were to follow the isothermal Path A-A’-A’’, then we would go below through the dew-point pressure, increase the volume percentage of the liquid hydrocarbon phase until it reached a maximum at Point A’ with further reductions in pressure resulting in a lower volume percentage of the liquid hydrocarbon phase. We could also continue the isothermal pressure reduction, reenter the single-phase gas region, and stop at Point A’’.
We can see from Figure 2.09 and Figure 2.10 that for a pure (single-component) system, the liquid phase occurs at higher pressures than the gas phase. Thus, if we were to start in the single-phase liquid region of a pure system, we would need to reduce the pressure isothermally to create a gas phase.
The analogy for our multi-component system is that if we start at the point of maximum liquid volume (Point A’ in Figure 2.16) and reduced the pressure isothermally, then we would get the conventional behavior for a pure system along Path A’-A’’. Conversely, if we were to start at Point A’ and increased the pressure isothermally to Point A in the single-phase gas region, then we would get the behavior opposite of that for a pure system along Path A’-A. This behavior, opposite to a pure system, is referred to as retrograde behavior. This behavior occurs in the green shaded region in Figure 2.16. This region, formed by connecting all of the points of maximum temperature on the quality lines, is referred to as the retrograde region of the fluid.

Sometimes we see or hear the terms “Retrograde Condensate Reservoir” or “Retrograde Condensate System.” This terminology is used to describe reservoirs in which the isothermal reservoir pressure-temperature path traverses the retrograde region of the system’s phase envelope.
2.12: Wet Gas Reservoirs
Wet gas reservoirs are gaseous hydrocarbon systems that reside in reservoirs with the original temperatures above the cricondentherm. In addition, the field surface facilities, separators, gas plant, etc., are in the two-phase region of the system’s phase diagram. This is shown in Figure 2.17. Under these conditions, as the pressure in the reservoir is reduced due to production, the reservoir never enters the two-phase region of the gas and no hydrocarbon liquids drop out in the reservoir. That is, as pressure is reduced, the hydrocarbon fluid in the reservoir remains in its gaseous state. However, as the produced gas travels up the well and to the surface, at some point in the production system it enters the two-phase region of the phase envelope and liquid hydrocarbons develop in the well or surface facilities.

2.13: Dry Gas Reservoirs
Dry gas reservoirs are gaseous hydrocarbon systems that reside in reservoirs with the original temperatures above the cricondentherm. In addition, the surface conditions are also greater than the cricondentherm. This is shown in Figure 2.18. Under these conditions, as the pressure in the reservoir is reduced due to production, both the fluids in the reservoir and the fluids in the production system remain a single gaseous phase.

2.14: Key Learnings
- Crude oil and natural gas exist in the ground in the pore spaces of reservoir rock, typically sedimentary rock.
- Crude oil and natural gas accumulate in the ground in structures known as hydrocarbon reservoirs.
- There are five elements that are required for a hydrocarbon reservoir. The absence of just one element will preclude a geological feature from acting as a hydrocarbon reservoir. The timing of the formation of these elements is critical; all elements must be in place before the migration of oil or gas begins. These elements are:
- the source rock
- the migration path
- the cap rock
- the trap
- reservoir quality rock
- The source rock is an organic-rich sedimentary rock where catagenesis converts dead organic material, predominantly dead algae and zooplankton, into kerogen and eventually hydrocarbons.
- The migration path is a pathway where mature oil and gas migrate from the source rock to the trap. During the migration process, buoyancy is the dominant force acting on the hydrocarbons.
- The cap rock is an impermeable rock that prevents lighter oil and gas from migrating vertically away from the trap and towards the surface.
- The trap is a specific geological structure that keeps the crude oil and natural gas in place over geological time (i.e., provides four-way closure to the oil and gas). Traps can either be stratigraphic in nature, where the trapping mechanisms are dominated by the layering of sedimentary rocks, or structural in nature, where the trapping mechanisms are dominated by the folding and faulting of the rocks.
- The reservoir rock is a rock that has sufficient reservoir quality to allow for commercial crude oil and natural gas accumulations:
- sufficiently high porosity to allow for the storage of crude oil and natural gas in commercial volumes;
- sufficiently high permeability to allow for the subsurface transport of crude oil and natural gas at commercial production rates.
- The prevailing theory is that the hydrocarbons that make up crude oil and natural gas are organic in nature.
- Crude oil and natural gas are complex mixtures of four hydrocarbon types:
- alkane hydrocarbons
- naphthenic hydrocarbons
- aromatic hydrocarbons
- asphaltene hydrocarbons
- The phase behavior of the complex mixtures of hydrocarbons are determined by the composition of the mixture and are governed by Gibbs Phase Rule.
- The original pressure and temperature of a hydrocarbon reservoir at discovery are determined by the local hydrostatic gradient and thermal gradient, respectively.
- Where the original pressure and temperature of the reservoir lies in the phase envelope of the phase diagram determines the type of crude oil or natural gas system that will be produced from the reservoir.
2.15: Summary and Final Tasks
Summary
In this lesson, we learned about the origin of crude oil and natural gas and their occurrence in subsurface reservoirs. In particular, we learned that subsurface reservoirs are composed of porous and permeable rocks and that there are five requirements for a crude oil or natural gas reservoir:
- the presence of a source rock where organic material accumulates and, over time, is converted to kerogen (a precursor to crude oil and natural gas) due to the subsurface heat and pressure;
- the presence of a migration path where hydrocarbons can migrate from the source rock to the reservoir;
- the presence of a cap rock to prevent the lighter oil and gas molecules from escaping from the reservoir to the surface because of their buoyancy in water;
- the presence of a reservoir rock to allow for (A) the accumulation of oil and gas in commercial quantities and (B) the producibility of fluids at commercial rates;
- the presence of a trap to provide a mechanism to contain the oil and gas over geologic time until discovery.
In addition, we discussed the two major classifications of hydrocarbon traps:
- stratigraphic traps where the trapping mechanism is dominated by the layering of the rock;
- structural traps where the trapping mechanism is dominated by the folding, faulting, and deformation of the reservoir rock.
We also saw that crude oil and natural gas is composed of hydrocarbon molecules of organic origin. These hydrocarbon molecules are categorized into four types:
- paraffinic (or alkane) hydrocarbons which are straight chain molecules (or branched-chain molecules call isomers);
- naphthenic (or saturated cyclic) hydrocarbons which are ringed molecules where all of the bonds between carbon atoms are single bonds;
- aromatic (or unsaturated cyclic) hydrocarbons which are ringed molecules where double bonds between carbon atoms are present;
- asphaltene hydrocarbons which are complex mixtures of chain and ring molecules.
We also saw that the dominant hydrocarbon type can be determined by the Watson Characterization Factor.
Finally, we discussed the basics of the phase behavior of the hydrocarbon accumulations. We saw that this phase behavior can be visualized in a Phase Diagram and can be quantified with tools, such as the Gibbs Phase Rule, among others (like Cubic Equations of State). We also saw that the phase envelopes shown in the Phase Diagrams, the initial reservoir pressure and temperature at discovery, the pressure-temperature path of the reservoir during production, and the pressure-temperature path of the fluids going up the well and through the surface equipment results in several types of hydrocarbon reservoirs. The hydrocarbon reservoirs that we discussed were:
- undersaturated and saturated black oil, or low-shrinkage, crude oil reservoirs;
- undersaturated and saturated volatile oil, or high shrinkage, crude oil reservoirs;
- gas condensate reservoirs (sometimes referred to as retrograde condensate reservoirs) where liquid hydrocarbons condense from the gaseous phase;
- wet gas reservoirs;
- dry gas reservoirs.
Final Tasks
Reminder - Complete all of the Lesson 2 tasks!
You have reached the end of Lesson 2! Double-check the to-do list on the Lesson 2 Overview page [16] to make sure you have completed all of the activities listed there before you begin Lesson 3.
Lesson 3: Reservoir Engineering: Rock and Fluid Properties
3.0: Lesson Overview
You will have two weeks to complete Lesson 3.
Lesson 3 is very extensive, and you will have two weeks to read through the lesson and complete the associated assignments. Please use your time wisely and don't let yourself fall behind; you will need the extra week to work your way effectively through the material.
Please refer to the Calendar in Canvas for specific time frames and due dates.
Overview
Petroleum engineers working in the upstream sector of the oil and gas industry must perform their analyses on the known properties of the reservoirs and reservoir fluids associated with the oil and gas fields they are tasked to manage. The properties that these petroleum professionals are most likely to use during their careers are:
- Rock properties
- Fluid properties
- Oil properties
- Gas properties
- Water properties
- Rock-Fluid interaction properties
These data are required for most routine calculations and are typically obtained with field or laboratory measurements. In cases where these data are unavailable due to time or cost constraints, industry accepted correlations are available for generating missing data. For detailed analyses, measured data are preferred; however, data from correlations serve a vital role of generating data for quick, low cost analyses. In this lesson, we will discuss the data used in petroleum engineering analyses. We will discuss what data are available, how the data are used in the field, how the data are measured in the field or laboratory, and what correlations are available to supplement missing data.
Learning Objectives
By the end of this lesson you should be able to:
- identify the units used in the oil and gas industry;
- list the data used by petroleum engineers on a daily basis during their careers;
- list the sources (field, laboratory, or derived from correlations) of these data;
- explain the basics of the field and laboratory procedures used to obtain these data;
- list and discuss the assumptions behind the field and laboratory measurements;
- calculate required data from raw laboratory or field measurements;
- calculate required data from industry standard correlations;
- describe the relationships and dependencies of the data;
- integrate rock, fluid, and rock-fluid interaction data to perform basic analyses, such as storage and flow rate calculations; and
- discuss the concept of fluid saturations and how these saturations impact storage and production of oil and gas.
Lesson 3 Checklist
| To Read | Read the Lesson 3 online material | Click the Oilfield Measures and Units link below to continue reading the Lesson 3 material |
|---|---|---|
| To Do | Lesson 3 Problem Set | Submit your solutions to the Lesson 3 Problem Set assignment in Canvas |
Please refer to the Calendar in Canvas for specific time frames and due dates.
Questions?
If you have questions, please feel free to post them to the Course Q&A Discussion Board in Canvas. While you are there, feel free to post your own responses if you, too, are able to help a classmate.
3.1: Oilfield Measures and Units
The domestic United States oil and natural gas industry uses a very specific set of measures and units that were common at the dawn of the industry and, at least in the U.S., have been retained and expanded upon over the years. These units are often called Oilfield Units. In the international oil and gas industry, the metric system or the related S.I. (Systeme Internationale) system are used. In this course, we will use the U.S. domestic, oilfield units.
The standard measure of volume in the U.S. oil and gas industry is the Barrel (bbl) for liquids and the cubic foot (ft3) for gases. The barrel is defined as 42 U.S. gallons. That is:
You have probably noticed that the unit for barrel, “bbl,” has two “b’s”, while the word for barrel only has one. One story relating the origin of the unit “bbl” and the measure of 42 U.S. gallons follows[2]:
In the early 1860s, when oil production began, there was no standard container for oil, so oil and petroleum products were stored and transported in barrels of all different shapes and sizes (beer barrels, fish barrels, molasses barrels, turpentine barrels, etc.). By the early 1870s, the 42-gallon barrel had been adopted as the standard for oil trade. This was 2 gallons per barrel more than the 40-gallon standard used by many other industries at the time. The extra 2 gallons was to allow for evaporation and leaking during transport [sic] (most barrels were made of wood). Standard Oil began manufacturing 42 gallon barrels that were blue to be used for transporting petroleum. The use of a blue barrel, abbreviated "bbl," guaranteed a buyer that this was a 42-gallon barrel.
In August of 1866, independent American oil producers met in Titusville, PA and agreed that the 42 gallon barrel would be the industry standard in the U.S.A. [3]
Because of the slightly compressible nature of liquids and the compressible nature of gases, the volume of a given mass of liquid or gas at one set of pressure and temperature conditions will not equal the same volume at a different set of pressure and temperature conditions. To provide a common measure of volume, we can specify the volume of a given mass measured at a reference pressure and temperature.

For liquids, the Upstream Oil Industry uses the pressure and temperature at Stock Tank Conditions as the reference conditions for discussing standardized volumes. The stock tank is the last vessel used in the field separation of crude oil and natural gas prior to the transport to other field processing plants (local oil or gas plants) or export to a distant refinery. The Stock Tank Pressure and Stock Tank Temperature make up a field dependent set of conditions which are determined by the pressure and temperature that maximizes the volume of the produced oil. In other words, a crude oil with a specific composition is produced from a reservoir and the field Separator and Stock Tank conditions are adjusted to maximize the volumetric yield of the crude oil. The pressure and temperature conditions that maximize the crude oil volume from one reservoir will be different from the pressure and temperature conditions that maximize the crude oil volume from another reservoir due to the difference in the crude oil compositions. Thus, the stock tank pressure and stock tank temperature in one oilfield may be different from the stock tank pressure and stock tank temperature in another oilfield. Representative stock tank conditions may be on the order of 100 psi and 75°F. Figure 3.02 shows a typical, three-stage, gas-oil Separation Train.

In this figure, the stock tank pressure and temperature, pST and TST, are the field-specific reference pressure and temperature used in all reservoir engineering calculations for crude oil and produced water. When referring to liquid volumes at stock tank conditions, we use the units of Stock Tank Barrels (STB).
For gases, we use Standard Conditions, pSC and TSC, as the reference conditions for volumetric reservoir engineering calculations. Standard conditions are defined by different governments, scientific agencies, industries, or in some instances, specific legal contracts. The Society of Petroleum Engineers (SPE) defines these conditions as pSC = 14.696 psi (101.325 kPa) and 59°F (15°C). Informally, many engineers use pSC = 14.7 psi and 60°F. The appropriate set of standard conditions to be used in engineering calculations will often be dictated by the company and the location where the engineer works. When referring to the gas volumes at standard conditions, we use the units of Standard Cubic Foot (SCF).
For volumetric rate calculations, the U.S. oil and gas industry uses the symbol “q” for the volume of oil or gas produced (or transported) over a 24-hour period. Thus, we have:
- qo = STB/day for oil (at stock tank conditions)
- qw = STB/day for water (at stock tank conditions)
- qg = SCF/day for gas (at standard conditions)
When we consider volumes at a field scale, we often need to use units greater than the stock tank barrel, STB, or the standard cubic foot, SCF. For this, the oil industry uses the uppercase letter “M.” This stands for thousands of STB or SCF. For example, the unit of MSTB refers to thousands of STBs, and the unit of MSCF refers to thousands of SCF. Likewise, the unit of MMSTB refers to millions of STBs, and the unit of MMSCF refers to millions of SCF.
| 1 MMSTB | = 1,000 MSTB | = 1,000,000 STB |
| 1 MMbbl | = 1,000 Mbbl | = 1,000,000 bbl |
| 1 MMSCF | = 1,000 MSCF | = 1,000,000 SCF |
| 1 MM ft3 | = 1,000 M ft3 | = 1,000,000 ft3 |
| 1 MMSTB/day | = 1,000 MSTB/day | = 1,000,000 STB/day |
| 1 MMSCF/day | = 1,000 MSCF/day | = 1,000,000 SCF/day |
[2] Source: Seeking Alphaα - Where Does That 2nd 'B' in the Abbreviation for Crude Barrels (BBL) Come From? [17]
[3]Source: American Oil & Gas Historical Society - History of the 42-Gallon Oil Barrel [18]
3.2: Reservoir Rock Properties
The reservoir rock properties that are of most interest to development geologists and reservoir engineers (amongst others) are Porosity, Compressibility, and Permeability. Porosity is a rock property that defines the fraction of the rock volume that is occupied by the pore volume. Compressibility is the rock property that governs the relative change in the pore volume when pressure is either increased or decreased. Finally, permeability is the rock property that is a measure of the ease (or difficulty) with which liquids or gases can flow through a porous medium.
Rock Porosity
As previously mentioned, porosity, ϕ, is the fraction of the Bulk Rock Volume, , that is occupied by the Pore Volume, . Mathematically, it is defined as:
The bulk volume, Vb, can also be defined as the sum of the volumes of the two constituents of the rock, pore volume and Grain Volume, Vg. That is:
From these two expressions, we can develop several equivalent definitions for porosity:
Figure 3.03 (below) shows the porosities for three different idealized grain packings. In this figure, the rock grains are the spheres and the pore volume is the space between the spheres. Note that the porosities of these three systems are independent on the radii of the grains. In a real rock, the grains would be angular (if quartz grains in sandstones) and some of the void space might be filled with smaller grains, mineral cementation, and clays.
 |
|
 |
|
 |
At this point, we must distinguish between two types of porosity in rock: Total Porosity, , and Effective Porosity, . Real reservoir rock is comprised of connected pores and isolated pores. As the name implies, connected pores are pores which are connected to other pores and are capable of transmitting fluids. Isolated pores are pores, or groups of pores, which do not connect to other pores or form dead-end pathways. These isolated pores are incapable of transmitting fluids. Total porosity is defined as the total pore space (connected plus isolated pores) divided by the bulk volume, while effective porosity is the connected pore volume divided by the bulk volume.
Reservoir engineers are concerned with how fluids are stored and flow in the reservoir. Consequently, reservoir engineers are more concerned with effective porosity,
The porosity is of primary concern to geologists and reservoir engineers because it is a direct measurement of the ability of a reservoir rock to store fluids. There are two ways that oil and gas professionals can obtain measurements of porosity through laboratory measurement and through the use of Well Logs.
3.2.1: Porosity from Laboratory Measurements
One method in which porosity is determined is by laboratory measurements of Core Samples brought to the surface during drilling. Measurement of porosity in the laboratory is part of Routine Core Analysis, sometimes referred to as PKS Analysis (porosity, permeability, and saturation analysis).
Core samples are rock samples that are cut from the reservoir formation using specialized Coring Bits. The extraction of core samples is a very complicated process and requires a lot of planning. When cutting a core, all phases of the coring process must be considered to ensure that the porosity is not altered prior to its delivery to the laboratory. These phases include core cutting, core handling, core preservation, core transport, core sampling, and core testing. Typically, a Formation Evaluation Specialist takes the lead role in designing the core program while working with a development geologist, a reservoir engineer, and a drilling engineer.
After retrieving representative core samples and delivering them to the laboratory, there are several methods that can be used to determine porosity. As shown in Equations 3.01 through 3.03, to determine porosity, we need to determine two of the three volumes, , , or . Once these are determined, then the porosity and the third volume are known.
Bulk Volume, , Determination
Bulk volume can be determined by one of two methods, physical measurement and displacement. The use of physical measurements is only applicable to core samples with regular geometric shapes. As the name implies, physical measurement involves the measurement of the dimensions of the core sample (typically a cylindrical core plug) and calculating the volume from standard volumetric formulae.
Displacement methods involve the immersion of the core sample in mercury inside of a pycnometer or graduated cylinder. Mercury is used in displacement methods to prevent invasion into the pore space. The bulk volume of the sample is the apparent volume change of the mercury in the pycnometer or graduated cylinder. Alternative, Archimedes’ Principle can be used to determine the bulk volume of the core sample from the apparent weight change due to buoyancy when fully immersed.
Grain Volume, , Determination
The most direct method for determining grain volume is to measure the weight of a dried sample and to divide by the density of the rock matrix. Unfortunately, the rock densities are often not accurately known.
A second method, similar to the immersion method for bulk volume determination, can be used for grain volume determination. In this method, a core sample is crushed and the resulting rock grains are placed into a pycnometer or graduated cylinder along with a known volume of liquid. The volume of the rock grains can then be determined from the apparent volume change of the liquid (the Russell Method) after immersion or the apparent weight change (the Melcher-Nutting Method) of the immersed sample due to buoyancy using Archimedes’ Principle.
Unfortunately, the disadvantage of this method is that it is destructive. Once the sample is pulverized, it cannot be used for further testing. Since we have crushed the core sample to its constituent rock grains, the porosity determined from the immersion of these grains is the total porosity, .
A third method is the Boyle’s Law Method. As the name implies, it uses Boyle’s Law for the grain volume determination:
In this method, the core sample is placed into one chamber of an experimental apparatus containing two chambers of known volume connected by a closed valve. An inert gas (helium or nitrogen) is introduced into the chambers at different, but known, pressures. At this point, the total number of moles, nT, in the apparatus can be determined from:
For isothermal conditions, this reduces to Boyle’s Law:
The valve between the chambers is opened and the pressure is allowed to stabilize to the final pressure, pf, and is recorded. If we assume that the core sample was placed into Chamber 1, then we have:
Example 3.01
Given the following data:
- Weight of the crushed core sample in air:
- Weight of the crushed core sample in water:
- Density of water:
Use Archimedes’ Principle to calculate the grain volume of the sample.
Solving for :
The advantages of this method are that it is non-destructive and can be very accurate. The disadvantage of this method is that for low permeability core samples, it may take a long time for the pressures to stabilize. Since the gases can only enter or leave the connected pores, the porosity obtained from the Boyle’s Law Method is the effective porosity, .
Pore Volume, , Determination
Early methods used for pore volume determination, such as the Washburn-Bunting Method, used mercury injection into the pore spaces of the core sample. In these Mercury Injection Methods, high pressure mercury was injected into the core sample and the volume of mercury entering the core was measured. These methods had several drawbacks, including the destructive nature of the test and the compression of any gases in the core sample retaining a residual volume, resulting in measurement inaccuracies.
Example 3.02
Given the data:
When the valve between Chamber 1 and Chamber 2 is opened, the pressure is found to stabilize at . What is the grain volume of the core sample?
A second method, the Resaturation Method, uses a clean dry core sample and resaturates it with a fluid of known density. The change in weight of the sample can then be used to determine the pore volume, Vp, of the sample
Since the fluid can only enter or leave the connected pores, the porosity obtained from the resaturation method is the effective porosity, .
A third method for the determination of the pore volume is the Summation of Fluids Method. In this method, a core sample in its native state (not cleaned or dried) is halved. In one of the halves, mercury injection is used to estimate the gas volume, while the second half is used in the retorting (distillation) process to determine the oil and water volumes. The pore volume is then set equal to the sum of the fluid volumes. The advantage of this method is that the Phase Saturations (fraction of the pore space occupied by each phase – oil, gas, and water) can be determined simultaneously with the porosity. The disadvantages of the method are the destructive nature of the test and the assumption that both halves of the core sample contain similar fluid volumes.
Again, in the summation of fluids method, fluids can only enter or leave the connected pores. Consequently, the porosity obtained from this method is the effective porosity, .
Example 3.03
Given the following data:
- Weight of the clean dried core sample in air:
- Weight of the core sample saturated with water:
- Density of water:
What is the pore volume of the core sample?
| Method | Porosity Type | Advantages | Disadvantages |
|---|---|---|---|
| Grain Determination by Immersion | Total Porosity, |
|
|
| Grain Determination by Boyles Law | Effective Porosity, |
|
|
| Washburn-Bunting (Mercury Injection) | Effective Porosity, |
|
|
| Resaturation | Effective Porosity, |
|
|
| Summation of Fluids | Effective Porosity, |
|
|
3.2.2: Porosity from Well Logs
The most common method of determining porosity is with Well Logs. Well logs are tools sent down the wellbore during the drilling process which measure different reservoir properties of interest to geologists and engineers. Due to the expense of obtaining core samples, typically only a few wells are cored. The wells that do get cored are usually wells early in the life of the reservoir (appraisal wells) and key wells throughout the reservoir. On the other hand, well logs are routinely run in wells, if only to identify the depths of the productive intervals. The three open-hole logs used to evaluate porosity are:
- The sonic log
- The density log
- The neutron log
While none of these logs measures porosity directly, the porosity can be calculated based on theoretical or empirical considerations. The measurements obtained from these logs are not only dependent on the porosity but are also dependent on other rock properties such as:
- Lithology (rock type: sandstone, limestone, shale, etc.)
- The fluids occupying the pore spaces
- The wellbore environment (type of drilling fluid, hole size)
- The geometry of the pores
Since many variables may impact the log readings, corrections need to be applied to the log interpretations and the three logs are typically evaluated together to determine the best estimate of the porosity of rock formations. The log evaluations are also calibrated against core porosity in wells where both core and logs are available.
The Sonic Log measures the acoustic transit time, Δt, of a compressional sound wave traveling through the porous formation. The logging tool consists of one or more transmitters and a series of receivers. The transmitters act as sources of the acoustic signals which are detected by the receivers. The time required for the signal to travel through one foot of the rock formation is the acoustic transit time, Δt. The acoustic travel time, then, is the reciprocal of the sonic velocity through the formation. The units of Δt are micro-seconds/ft (μsec/ft) or millionths of a second per foot.
There are several ways to interpret the sonic log measurements. One of the most common interpretation formulae is the Wyllie Time-Average Equation:
Where:
- ϕsl is the porosity from the sonic log (log measurement) , fraction
- Δtsl is value of the acoustic transit time measured by the sonic log, μsec/ft
- Δtma is value of the acoustic transit time of the rock matrix measured in the laboratory, μsec/ft
- Δtf is value of the acoustic transit time saturating fluid measured in the laboratory, μsec/ft
The presence of hydrocarbons in the reservoir rock results in an over prediction of porosity measured by the sonic log and some corrections may be required. These corrections take the form:
or,
Table 3.03 has typical values of the acoustic transit time for different reservoir formations and commonly encountered reservoir fluids.
| Heading1 | Δtma (μsec/ft) Range |
Δtma (μsec/ft) Commonly Used |
Δtf (μsec/ft) Range |
Δtf (μsec/ft) Commonly Used |
|---|---|---|---|---|
| Sandstone | 55.5 – 51.0 | 55.5 or 51.0 | — | — |
| Limestone | 47.8 – 43.5 | 47.5 | — | — |
| Dolomite | 43.5 | 43.5 | — | — |
| Anhydrite | 50.0 | 50.0 | — | — |
| Salt Formation | 66.7 | 67.0 | — | — |
| Fresh Water Based Drilling Fluid |
— | — | 189.0 | 189.0 |
| Salt Water Based Drilling Fluid |
— | — | 185.0 | 185.0 |
| Gas | — | — | 920.0 | 920.0 |
| Oil | — | — | 230.0 | 230.0 |
| Casing (Iron) | — | — | 57.0 | 57.0 |
Other empirically based equations exit for sonic log interpretation. One form of an alternative equation is:
In this equation, the value of C is in the range of 0.625 to 0.700 and is determined by calibrating the equation to known porosity, such as, to core data when a well is both cored and logged. In Equation 3.12 and Equation 3.13, ϕsonic is the final interpreted porosity from the sonic log.
The Density Log measures the electron density ρe, of the formation (the electron density is the number of electrons per unit volume). The density logging tool emits gamma rays from a chemical source which interact with the electrons of elements in the formation. Detectors in the tool count the returning gamma rays. These returning gamma rays are related to the election density of the elements in the formation.
The electron density is proportional to the bulk density, ρb, of the formation (the bulk density is the density of the fluid-filled rock in grams per unit volume). For a molecular substance, this proportionality is:
Where:
- is the electron density of the formation, electrons/cc
- is the bulk density of the formation, gm/cc
- ΣZ is the sum of the atomic numbers making up the molecule, electrons/molecule
- MW is the molecular weight, gm/molecule
Table 3.04 contains the term in the parenthesis for common substances related to oil and gas production.
| Compound | Chemical Formula |
Actual Density, (gm/cc) |
(electrons/gm) |
Electron Density, (electrons/cc) |
Log Reading, Apparent (gm/cc) |
|---|---|---|---|---|---|
| Quartz | SiO2 | 2.654 | 0.9985 | 2.650 | 2.648 |
| Calcite | CaCO3 | 2.710 | 0.9991 | 2.708 | 2.710 |
| Dolomite | CaCO3MgCO3 | 2.870 | 0.9977 | 2.863 | 2.876 |
| Anhydrite | CaSO4 | 2.960 | 0.9990 | 2.957 | 2.977 |
| Sylvite | KCl | 1.984 | 0.9657 | 1.916 | 1.863 |
| Halite | NaCl | 2.165 | 0.9581 | 2.074 | 2.032 |
| Gypsum | CaSO42H2O | 2.320 | 1.0222 | 2.372 | 2.351 |
| Anthracite Coal | --- | 1.400 - 1.800 | 1.0200 | 1.442 – 1.852 | 1.355 – 1.796 |
| Bituminous Coal | --- | 1.200 - 1.500 | 1.0600 | 1.227 – 1.590 | 1.173 – 1.514 |
| Fresh Water | H2O | 1.000 | 1.1101 | 1.110 | 1.000 |
| Brine (200,000 ppm) | --- | 1.146 | 1.0797 | 1.237 | 1.135 |
| Oil | N(CH2) | 0.850 | 1.1407 | 0.970 | 0.850 |
| Methane | CH4 | 1.2470 | 1.247 | 1.335 - 0.1883 | |
| Gas | --- | 1.2380 | 1.238 | 1.238 - 0.1883 |
One important observation from this table is that the column containing the group in parenthesis in Equation 3.14, , is approximately 1.0. Since this term is close to unity, the electron density is a very close approximation to the bulk density, as also seen in Table 3.03. The logging tool is calibrated by running it against a limestone formation containing fresh water. With this calibration, the Log Reading, Apparent ρba (last column in Table 3.03) is:
For some substances, such as liquid-filled sandstones, limestones, and dolomites, ρba can be used directly as ρb. For other substances, such as sylvite, rock salt, gypsum, anhydrite, coal, and gas bearing formations, further corrections are required. These additional corrections are beyond the scope of this course. Once the bulk density is determined, the porosity can be estimated by:
Where:
- ϕdensity is the final interpreted porosity from the density log, fraction
- ρma is the matrix density (from the Actual Density, ρb, Column in Table 3.03), gm/cc
- ρb is bulk density from density log (Equation 3.15), gm/cc
- ρf is the density of the fluid measured in the laboratory, gm/cc
The Neutron Log measures the amount of hydrogen in the formation being logged. Since the amount of hydrogen per unit volume is approximately the same for oil and water, the neutron log measures the Liquid Filled Porosity (the porosity excluding the Gas-Filled Porosity). The neutron logging tool emits neutrons from a chemical source which collide with nuclei of elements in the formation. The element in the formation with the mass closest to a neutron is hydrogen. Due to the parity in mass, the neutron in a neutron-hydrogen collision loses approximately half of its energy. With enough collisions, the neutron eventually loses enough energy and is absorbed by the hydrogen nucleus and a gamma ray is emitted. The neutron logging tool measures these emitted gamma rays. Note, other hydrogen atoms may be present in clays in the rock, or in the rock itself and corrections for these other hydrogen atoms are required.
Interpretation of the neutron log is performed by first calibrating the logging tool to specific well and formation conditions. Interpretation charts supplied by the logging company are used to interpret the log for deviations from these calibration conditions. The interpretation of the neutron log for ϕneutron is beyond the scope of this course.
As mentioned throughout the discussion on porosity logging, due to the various wellbore and formation conditions encountered during the logging operations (i.e., real conditions, as opposed to laboratory conditions) many corrections may be required to get a good interpretation from the different well logs. In addition, the logs are typically evaluated together to aid in the interpretation. Finally, if core data are available from a well, then the core derived porosity is used to calibrate the logging tools.
Rock (Pore-Volume) Compressibility
In addition to the porosity and its relation to pore-volume, reservoir engineers are also interested in how the pore-volume behaves (increases or decreases) with increases or decreases in pore-pressure. The industry standard relationship for change in pore-volume is based on the isothermal pore-volume compressibility, cPV.
The isothermal pore-volume compressibility is always positive and is defined as:
The units of compressibility are 1/psi. Equation 3.17 implies that as pressure increases the pore-volume increases. Hall [4] correlated the effective rock compressibility as a function of porosity which is shown in Figure 3.04.

For a constant bulk volume and compressibility, we can separate variables in Equation 3.17 and integrate to arrive at the following relationship between pore-volume (or porosity) and pore pressure:
or,
Where ϕref is a reference porosity measured at reference pressure, pref. After some manipulation:
To further simplify this relationship, if we assume a small pore-volume compressibility (as shown in Figure 3.03, we are typically dealing with rock compressibilities on the order of 10-6 1/psi) and apply a Taylor Series expansion to the exponential function (truncated after one term), we obtain:
The rock compressibility determination is performed in the laboratory on core samples. The rock compressibility is an expensive test to run and is not part of the Routine Core Analysis. It must be specifically requested as part of any Special Core Analysis, or SCAL, testing performed on the core sample.
Rock Permeability
The permeability of a porous medium is a measure of the ease (or difficulty) in which a fluid can flow through the pores of the medium. Permeability is a property of the porous medium which in our case is the reservoir rock. The unit of permeability is the Darcy, or D, named after the French engineer Henri Darcy who investigated the flow of water through filter beds in the city of Dijon in the mid-1800s. The unit of Darcy has the dimensions of length-squared. One significant contribution from Darcy’s work (among many), is Darcy’s Law, which was published in 1856 and forms one of the foundations of porous media flow:
Where:
- qw is the flow rate of water, cc/sec
- k is the permeability of the medium, Darcy
- A is cross-sectional area, cm2
- l is the length in the direction of flow, ft (x, y, or z in Cartesian coordinates)
- is the pressure gradient, atm/cm
The unit of the Darcy is defined as the permeability, k, required to allow a flow rate, qw, of one cc of water per second through a medium with a cross-sectional area, A, of one cm2, with an applied pressure gradient, Δp/ΔL, of one atm/cm. As it turns out, the Darcy as a unit is too large for most field applications. In reservoir engineering we typically work with the millidarcy, md, which is one one-thousandth of a Darcy:
Henri Poiseuille later generalized Darcy’s Law to fluids other than water by noting that the flow rate was inversely proportional to the dynamic viscosity, μf, of the fluid flowing through the porous medium. The unit of dynamic viscosity, the poise, is named after Poiseuille and is a property of the fluid. Again, as it turns out, the poise as a unit is also too large for most field applications. In reservoir engineering we typically work with the centipoise, cp, which is one one-hundredth of a poise:
The generalized form of Darcy’s Law for any single-phase fluid which incorporates the fluid viscosity is:
Darcy’s Law has several important assumptions associated with it. These include:
- A rigid porous medium (incompressible medium with no transport of rock grains, e.g. fines movement
- An incompressible, homogeneous, Newtonian fluid that fully saturates (single-phase) the porous medium
- Steady-state, isothermal, and laminar (low Reynolds number) flow conditions
- No interactions between the porous medium and the fluid flowing through it
- A no-slip interface between the porous medium and the fluid flowing through it (zero velocity boundary condition at the rock-fluid interface)
The form of Darcy’s Law discussed so far uses the SI unit system. For oilfield units, we have:
Where:
- qf is the flow rate of the saturating fluid, bbl/day
- 0.001127 is a unit conversion constant
- k is the absolute permeability of the medium, md
- A is cross-sectional area, ft2
- is the pressure gradient, psi/ft
Measurement of the permeability can be done through laboratory or field measurements. In the laboratory, a core sample of known dimensions (A and ΔL) is cleaned and placed into a fluid-tight core holder. A fluid of known viscosity (typically air) is allowed to flow through the core at a metered flow rate. Darcy’s Law is then used to calculate the permeability of the core sample.
In the field, permeability is measured with a Well Test using Pressure Transient Analysis. Under certain conditions, the production rate(s) (can be a zero-production rate) results in well pressures that honor known solutions to the Diffusivity (or Well Test) Equation. When the well test results are compared to the solutions to the diffusivity equation, the permeability of the formation can be estimated.
One common well test is a Pressure Build-Up Test. In a pressure build-up test, the well is produced at a stable (constant) rate, qp, for a production time of tp. The well is then shut in and the pressure is monitored during the shut-in period Δt; where Δt is measured from the beginning of the well is shut-in. The well test is called a build-up test because when the well is shut in, the pressures increase with increasing Δt. One analysis tool for the pressure build-up test is the Horner Plot. A typical Horner plot is shown in Figure 3.05.
In this plot shown in Figure 3.05, pws are the shut-in well pressures measured during the well test, tp and Δt are times in hours (Δt measured from the time that the well is shut-in), qp is the stabilized production rate during the production period prior to well shut-in in STB/day, μo is the oil viscosity in cp, Bo is the Formation Volume Factor in bbl/STB, k is the permeability in md, and h is the reservoir thickness in ft.
In a Horner Plot, the function , decreases as increases. As can be seen in this figure, the slope of the Horner Plot is related to the permeability of the reservoir near the well. If the shut-in pressures, pws, are measured and the slope calculated, then the permeability can be determined if all the other parameters in the definition of the slope are known.
In semi-logarithmic plots (plots with one conventional axis and one logarithmic axis), such as that in Figure 3.05, the slope is normally taken over one logarithmic cycle. That is:
While there is no universal correlation between permeability, field measurements suggest that as the porosity of a formation increases, the permeability of the formation also increases. This behavior is captured in a permeability-porosity cross-plot. One such example of a permeability-porosity cross plot is illustrated in Figure 3.06.
A permeability-porosity cross-plot is a field dependent transform that relates core derived permeability to core derived porosity. Note that the permeability-porosity transform shown in Figure 3.06 is plotted on a semi-logarithmic plot with the permeability plotted on the logarithmic scale. Also note that in the middle of the plot (ϕ = 20 percent) there is an approximate four order of magnitude error bar in the permeability data. This is typical for a permeability-porosity transform. While the results from these transforms may be crude, they are often the only source of permeability data when building complex models of oil or gas reservoirs. Note, geologists have developed methods for capturing this scatter into their models in the form of Scatter Plots, but the development of such plots is beyond the scope of this course.
The permeability in the presence of a single-phase fluid is called the absolute permeability. Since we will be dealing with multi-phase flow, we will need to discuss extensions to Darcy’s which allow for more than one phase. We will do this later in this lesson when we discuss Reservoir Rock-Fluid Interaction Properties.
3.3: Reservoir Fluid Properties
Reservoir fluid properties are normally measured in the laboratory. Pressure-Volume-Temperature (PVT) properties relate these properties to each other at equilibrium conditions. These variables, typically used for volumetric related reservoir behavior, are measured in a laboratory PVT Cell. A PVT Cell is a high-pressure vessel (container) that allows for the control and measurement of pressure, volume, and temperature.
In addition to laboratory measurements, reservoir PVT properties can be determined from Equations-of-State (EOS). Equations-of-state are theoretically derived equations that relate the State Variables: pressure, volume, and temperature (state variables are variables that define the thermodynamic state of a system). Three common examples of equations-of-state include:
Isothermal compressibility:
Real gas law:
Van der Waal’s Cubic EOS:
In Equation 3.26, the negative sign is required because the volume of a fluid decreases as pressure increase (i.e., the derivative is negative). Note that all of these relationships allow for the determination of one of the state variables, p, V, or T, if the two other variables are known (two degrees of freedom). For the isothermal compressibility EOS, Equation 3.26, temperature can be considered a variable if we have tables or equations where the value of cf can be defined for a specific temperature.
In addition to the equations-of-state, fluid PVT correlations are also used in the oil and gas industry. These correlations can be either graphical or mathematical in nature. Fluid property correlations are simply plots, curve fits, or regressions of many laboratory measurements covering a wide range of data. In general, these correlations may not be as accurate as laboratory measurements or equations-of-state, but they have their uses in reservoir engineering.
3.3.1: Water Properties
All oil and gas reservoirs have water associated with them. Since it is a common part of the system, we will need to discuss how it is stored and moves in the reservoir.
Water Formation Volume Factor, Bw
The water (or more correctly, the brine) Formation Volume Factor, Bw, (sometimes referred to as the FVF) is a pressure and temperature dependent property that relates the volume of 1.0 stock tank barrel, STB, of water to its volume in barrels, bbl, at another pressure. It has the units of bbls/STB. We have already discussed the use of the stock tank pressure and temperature as an oilfield reference system.
By definition, if we had 1.0 STB of water at pST and TST, and that same STB occupied 1.02 bbls at reservoir conditions, pr and Tr, then it would have a formation volume factor of:
We can also define the formation volume factor in terms of densities at stock tank conditions and at reservoir conditions. If we assume the mass of 1.0 STB, m1 STB, then at reservoir conditions, we would have:
which implies:
Water Isothermal Compressibility, cw
Water is considered to be a slightly compressible liquid with a very low value of compressibility. From Equation 3.26 we have:
One correlation for water compressibility[5] , cw, is:
Where:
- p is the pressure, psi
- C is the salt concentration, gm/L
- T is temperature, °F
We can develop an explicit formula for the water formation volume factor based on the water compressibility. If we take 1.0 STB of water and its volume in barrels at a reservoir pressure and temperature, then we would have: Vw (bbl) = Bw (pr, Tr) (bbl/STB) x 1.0 STB. Now,
or,
Water Viscosity, μw
In the laboratory, the water viscosity is measured with an apparatus called a Viscometer. The mechanics and test procedures for a viscometer are beyond the scope of this course, and we will work with known correlations. One correlation from McCain has the form:
with
and
where
- μw 14.7 psi is the water viscosity at 14.7 psi and temperature, T °F
- S is the salt concentration in weight percent, Wt% (note different unit from Equation 3.31)
Once the viscosity at 14.7 psi and T °F are determined, the water viscosity at other pressures can be determined from:
Water Density, ρw
The density of water is also a property of interest in petroleum engineering. McCain[6] provides the following correlation for estimating the water density at reference conditions:
where
- ρw ST is the water density at sock tank conditions, lb/ft3
- S is the salt concentration in weight percent, Wt%
The water density at reservoir conditions can then be calculated using Equation 3.29.
[5] Petro Wiki: Produced water compressibility [19]
[6] McCain, W.D. Jr.: McCain, W.D. Jr. 1990. The Properties of Petroleum Fluids, second edition. Tulsa, Oklahoma: PennWell Books.
3.3.2: Crude Oil Properties
As discussed in Lesson 2, crude oil is a complex mixture of hydrocarbon molecules. As engineers, we are interested in the bulk (large scale) properties of the crude oil and natural gas. As discussed earlier, these properties are typically measured in the laboratory PVT cell. A PVT cell is essentially a piston which allows the volume to be either increased or decreased. It is fitted with a pressure gauge to allow for pressures to be recorded; a measuring device to allow for the determination of the volume of the cell; and temperature control to ensure the test is conducted at the desired temperature.
For reservoirs containing black oils, the laboratory experiment used to determine PVT properties is the Differential Liberation Test. This test is illustrated in Figure 3.07.

In a differential liberation test, a crude oil sample (green) is introduced into the cell at the initial reservoir pressure and temperature (Step 1 in Figure 3.07). The volume of the cell is then increased by extending the piston outward (Step 2), and the pressure and volume are recorded. At Step 2, the pressure in the cell will be less that the original pressure due to the expansion of the crude oil. This process is continued for several pressure steps until the first bubble of gas (red) is observed through a window in the cell (Step 3). This pressure is the bubble-point pressure of the crude oil. Up until the bubble-point pressure is reached, all measurements have been single-phase (liquid hydrocarbon) measurements.
After the bubble-point pressure has been reached, the volume is increased further until a significant volume of free gas has developed (Step 4). At this point, the pressure and the oil and gas volumes in the cell are measured. The gas is then expelled from the piston under isobaric (constant pressure) conditions by reducing the piston volume and allowing the gas to escape through a valve in the system (Step 5). This process is then repeated until the desired final pressure is reached (Step 8). The pressure, liquid volume, and gas volume are then used in the calculation of the appropriate properties for black oils.
What is the differential liberation test trying to model? In the reservoir, as gas comes out of solution, it typically has a much lower viscosity than the oil phase. Consequently, as gas evolves from the oil, this difference in the viscosity allows the gas to move faster than the oil and to separate from the source oil from which it evolved. This is illustrated in Figure 3.08. In addition, due to the density differences between oil and gas phases, gravity will also act to separate the two phases. It is the properties of the separated phases that we are most interested in, as these are more representative of the processes occurring in the reservoir.

API Gravity of the Crude Oil, °API
In the oil and gas industry, crude oils are characterized by the API gravity (American Petroleum Institute gravity) of the oil. The units of the API gravity are degrees, °API (read as degrees API). The API gravity is defined as:
Where:
- ϒo is the specific gravity of the crude oil at 60 °F, dimensionless
- °API is the API gravity, degrees API
The API gravity scale acts as an inverse relationship to density (and specific gravity), that is, as density increases, the API gravity decreases. Crude oils are often graded by their API gravity:
- Light crude oil: °API > 31.5°
- Intermediate crude oil: 22.1° ≤ °API ≤ 31.5°
- Heavy crude oil: °API < 22.1o
Molecular Weight of the Crude Oil, MWo
Samples of the crude oil taken during the differential liberation test can be extracted from the PVT cell, and the compositions of the crude oil samples can be measured as functions of pressure. If the mole fractions, xi, of all components are measured from an oil sample (any sample, not just a sample from a differential liberation test), then the molecular weight in lbs/lbs-mole of the oil sample, MWo, can be calculated from:
If laboratory data are unavailable, then the Cragoe[7] correlation can be used to estimate the molecular weight:
Where:
- MWo is the molecular weight of the crude oil, lb/lb-mole
- °API is the API gravity, degrees API
Bubble-Point Pressure of the Crude Oil, pb
As already discussed, the bubble-point pressure is the pressure that first bubble of gas evolves from an undersaturated crude oil during pressure reduction. The laboratory method for calculating the bubble-point pressure, pb, of a crude oil was discussed earlier in the context of the differential liberation test. Other PVT tests, such as the Constant Composition Expansion Test, can be used to determine the bubble-point pressure of the crude oil. The constant composition expansion test is similar to the differential liberation test, however, the evolved gas is not expelled from the PVT cell during the test. For all measurements made up to and including the bubble-point pressure, the constant composition expansion test and the differential liberation test give identical results.
When measured data are not available, Standing’s correlation[8] can be used to estimate the bubble-point pressure:
with
Where:
- Rso is the solution gas-oil ratio of the crude oil, SCF/STB (to be discussed)
- ϒg is the gas gravity (MWg/MWair), dimensionless (to be discussed)
- T is the temperature, °F
- °API is the API gravity, degrees API
Solution Gas-Oil Ratio, Rso
As we have discussed, most crude oils (possibly excluding some extremely heavy crude oils: °API ≈ 10°) contain Dissolved Gas. This dissolved natural gas consists mostly of the low-end molecular weight hydrocarbons (methane, ethane, propane, and butane) and some inorganic impurities (nitrogen, carbon-dioxide, hydrogen-sulfide, etc.). The volume of this dissolved gas is quantified by the Solution Gas-Oil Ratio, Rso (sometimes simply referred to as Rs). The solution gas-oil ratio is defined as the volume of gas, measured is SCF or MSCF, in solution in 1.0 STB of crude oil. As such, it has the units of SCF/STB or MSCF/STB. A typical plot of Rso is illustrated in Figure 3.09.

In this figure, we can see that the reservoir is an undersaturated oil reservoir. The initial reservoir pressure, pi, is greater than the bubble-point pressure. If this reservoir were to undergo pressure depletion from oil production, then the average reservoir pressure would decline over time, and the pressure would eventually reach the bubble-point pressure. During this time period, the volume of gas in solution in the crude oil remains constant at the initial value of Rso i.
Once the reservoir pressure reaches the bubble-point pressure, pb, gas begins to come out of solution. As the gas comes out of solution and evolves into Free Gas, the volume of gas remaining in solution, Rso, must decrease. This is the behavior observed in Figure 3.09. The volume of free gas liberated from the original stock tank barrel can be calculated as (Rso i – Rso) in SCF/STB or MSCF/STB.
The laboratory procedure for determining the solution gas-oil ratio was discussed in terms of the differential liberation test. The Rso values are calculated by summing the appropriate gas volumes obtained during the differential test and dividing by the final oil volume. When this is done, all volumes need to be corrected back to the reference volumes of STB and SCF to get to the appropriate Rso curve.
When laboratory derived Rso data are unavailable, then Equation 3.41 and Equation 3.42 can be used to estimate the solution gas-oil ratio. This is done by placing an assumed pressure into Equation 3.42 and using Equation 3.41 to calculate the pressure associated with that assumed Rso value (not the bubble-point pressure as explicitly written in the equation).
Oil Formation Volume Factor, Bo
The Oil Formation Volume Factor, Bo, is comparable to the water formation volume factor. It relates volume of 1.0 STB of crude oil at stock tank conditions, pST and TST, to its volume at reservoir conditions, pr and Tr. A typical plot of Bo is illustrated in Figure 3.10.

This figure shows the formation volume factor of the crude oil for the same reservoir as that shown in Figure 3.09 (identical pi and pb). As the pressure depletes from the initial pressure to the bubble-point pressure, the formation volume factor increases. This is indicative of the crude oil expanding (remember, the formation volume factor is based on 1.0 STB of oil – when the FVF increases, it is because the volume in reservoir barrels, bbl, of that STB is getting larger). This is the typical behavior that would be expected by a slightly compressible fluid - as confining pressure is reduced, we would expect that the volume would expand.
When the reservoir pressure reaches the bubble-point pressure, the formation volume factor begins to decrease. This is indicative of the crude oil shrinking. This is the opposite of the expected behavior of a slightly compressible fluid. This implies that as confining pressure is reduced the volume of the crude oil gets smaller. The reason for this behavior is that the crude oil is composed of the liquid hydrocarbon and the gas dissolved in it. As the gas comes out of solution, the crude oil loses the volume occupied by the solution gas.
Oil FVF above the Bubble-Point Pressure Pressure, p > pb
Because the formation volume factor of crude oil behaves differently above and below the bubble-point pressure, we must use correlations that show the proper trends. Since the crude oil behaves as a typical slightly compressible fluid above the bubble-point pressure, we can use the definition of compressibility, Equation 3.32, above the bubble-point pressure:
and
Where, for crude oils, we use pb as the reference pressure.
Oil FVF below the Bubble-Point Pressure, p < pb
Below the bubble-point pressure, we can use Standing’s correlation[8] to estimate the oil phase formation volume factor:
with
Where:
- Bo is the oil formation volume factor, bbl/STB
- Rso is the solution gas-oil ratio of the crude oil, SCF/STB
- ϒg is the gas gravity (MWg/MWair), dimensionless (to be discussed)
- ϒo is the oil specific gravity (ρo/ρw), dimensionless
- T is the temperature, °F
These equations are valid below and up to and including the bubble-point pressure. Therefore, we can use these equations to generate Bob for Equation 3.43b if it is unavailable from laboratory measurements.
Oil Phase Compressibility above the Bubble-Point Pressure, p > pb
As discussed, above the bubble-point pressure, crude oil acts like a slightly compressible fluid. One correlation for oil phase compressibility, co, above the bubble-point pressure from Vazquez and Beggs[9] is:
Where:
- co is the oil compressibility, 1/psi
- Rso is the solution gas-oil ratio of the crude oil (for p > pb; Rso = Rso i), SCF/STB
- T is the temperature, °F
- ϒg is the gas gravity (MWg/MWair), dimensionless (to be discussed)
- °API is the API gravity, degrees API
- p is the pressure, psi
Oil Phase Compressibility below the Bubble-Point Pressure, p ≤ pb.
Crude oil above the bubble-point pressure can contain large amounts of dissolved solution gas (high values of Rso). At higher Rso values, the crude oil has higher compressibility values due to the solution gas. At pressures below the bubble-point pressure, gas comes out of solution and the compressibility values begin to get smaller as the crude oil tends to behave more and more like a Dead Oil (dead oil is gas free oil; while crude oil with dissolved gas is often referred to as Live Oil). One common correlation for oil phase compressibility, co, below the bubble-point pressure from McCain, Rollins, and Villena[10] is:
Equation 3.46b
Where:
- co is the oil compressibility, 1/psi
- p is the pressure, psi
- T is the temperature, °F
- °API is the API gravity, degrees API
- Rso b is the solution gas-oil ratio of the crude oil at pb (Rso b = Rso i), SCF/STB
Oil Phase Density above the Bubble-Point Pressure, p > pb
One the values of pb, Rso, ϒg, Bo, and co are determined (either by laboratory measurements or by correlations), the oil phase density itself is specified (there are degrees of freedom remaining for ρo). As we discussed earlier, above the bubble-point pressure, crude oil behaves like a slightly compressible fluid. As such, we can use the definition of compressibility based on density:
Now, if we assume 1.0 STB of oil, at reservoir conditions, then we have:
and
Substituting Equation 3.48 into Equation 3.47 results in:
After integration of Equation 3.49 we have:
Oil Phase Density below the Bubble-Point Pressure, p ≤ pb
Below the bubble-point pressure, the crude oil loses mass (mass of the liberated gas), so we must account for the mass of the liquid oil and the mass of the gas remaining in solution when estimating the oil density below the bubble-point pressure. We can do this with a simple material balance. Below (and up to) the bubble-point pressure, the density of the crude oil can be calculated by dividing the total mass of the oil plus dissolved gas by the total volume. In terms of the properties discussed so far, we have:
Where:
- ρo is the oil density, lb/ft3
- ρo ST is the density of the dead oil (gas free oil) at stock tank conditions, lb/ft3
- ϒg is the gas gravity (MWg/MWair), dimensionless (to be discussed)
- Rso is the solution gas-oil ratio of the crude oil at pr and Tr, SCF/STB
- Bo is the oil phase formation volume factor at pr and Tr, bbl/STB
Note that we can use the properties in at the bubble-point pressure, Rso i and Bob, in Equation 3.51 to obtain ρob for input into Equation 3.50.
Oil Phase Viscosity above the Bubble-Point Pressure, p > pb
The viscosity of a crude oil is also impacted by the amount of gas in solution. The typical viscosity behavior of crude oil is shown in Figure 3.11.

Oil Phase Viscosity below the Bubble-Point Pressure, p ≤ pb
The estimation of the oil viscosity below the bubble-point pressure is a two-step process. In the first step, the dead oil (gas free) viscosity is calculated and in the second step the live oil (oil with solution gas) viscosity is calculated. The dead oil viscosity at reservoir temperature can be calculate by[11]:
The second step is to calculate the live oil viscosity with the dissolved gas:
with
and
Where:
- A and B are correlation parameters
- μoD is the dead oil at Tr, cp
- °API is the API gravity, degrees API
- T is the temperature, °F
- Rso is the solution gas-oil ratio of the crude oil at pr and Tr, SCF/STB
Oil Phase Viscosity above the Bubble-Point Pressure, p > pb
The oil viscosity above the bubble-point pressure can found by calculating the viscosity at the bubble-point pressure, μob and Rso i, and adjusting it to higher pressures[11]:
with
Where:
- C is a correlation parameter
- μob is the live oil viscosity at pb and Tr, cp
- p is the pressure of interest, psi
- pb is the bubble-point pressure, psi
[7] Cragoe, C.S.: “Thermodynamic Properties of Petroleum Products,” U.S. Dept. of Commerce, Washington, DC (1929) 97.
[8] Standing, M.B.: Volumetric and Phase Behavior of Oil Field Hydrocarbon Systems, SPE, Richardson, TX (1977) 124.
[9] Vazquez, M. and Beggs, H.D.: "Correlations for Fluid Physical Property Prediction," JPT (June 1980) 968-70.
[10] McCain, W.D. Jr., Rollins, J.B., and Villena, A.J.: "The Coefficient of Isothermal Compressibility of Black Oils at Pressures Below the Bubblepoint," SPEFE (Sept. 1988) 659-62; Trans., AIME, 285. 10.
[11] W.D. McCain .Jr. “Reservoir·Fluid Property Correlations-State of the Art,” SPE Reservoir Engineering, (May 1991) p. 266.
3.3.3: Natural Gas Properties
For natural gases we are also most interested in the Gas Formation Volume Factor, Bg, and the Gas Viscosity, μg, as these properties strongly influence gas storage (and accumulation) and gas flow. For most reservoir engineering calculations, the gas formation volume factor (and Gas Compressibility, cg, and Gas Density, ρg) can be determined from the Real Gas Law, Equation 3.27:
Where:
- p is the pressure of interest, psi
- V is the volume, ft3
- Z is the oil super-compressibility factor, dimensionless
- R is the gas constant, (psi ft3) / (lb-moles °R)
- T is temperature, °R (°R = °F + 460.67)
Gas Super-Compressibility Factor, Z
The gas supercompresibility factor, Z (or Z-Factor, or Real Gas Deviation Factor), is a function of pressure and temperature that corrects the Ideal Gas Law for high pressure and high temperature conditions. In the oil and gas industry, the z-factor correlation for hydrocarbon gases that is universally accepted in the Standing-Katz Correlation[12]. This correlation is shown graphically in Figure 3.12.
As illustrated in Figure 3.12 The Standing-Katz Correlation correlates the z-factor to the Pseudo-Reduced Pressure, ppr, and Pseudo-Reduced Temperature, Tpr. The pseudo-reduced properties are defined by:
and
Where:
- p is the pressure of interest, psi
- ppc is the pseudo-critical pressure, psi
- T is temperature of interest, °R
- Tpc is pseudo-critical temperature, °R
All of these properties are called pseudo-properties because the pseudo-critical pressure and pseudo-critical temperature are not the true, measured critical properties, but are calculated properties:
and
with
Where:
- ppc is the pseudo-critical pressure, psi
- Tpc is the pseudo-critical temperature, °R
- ϒg is the gas gravity (MWg/MWair), dimensionless
- MWg is the molecular weight of the gas, lb/lb-mole
- MWair is the molecular weight of air, lb/lb-mole (28.97 lb/lb-mole)
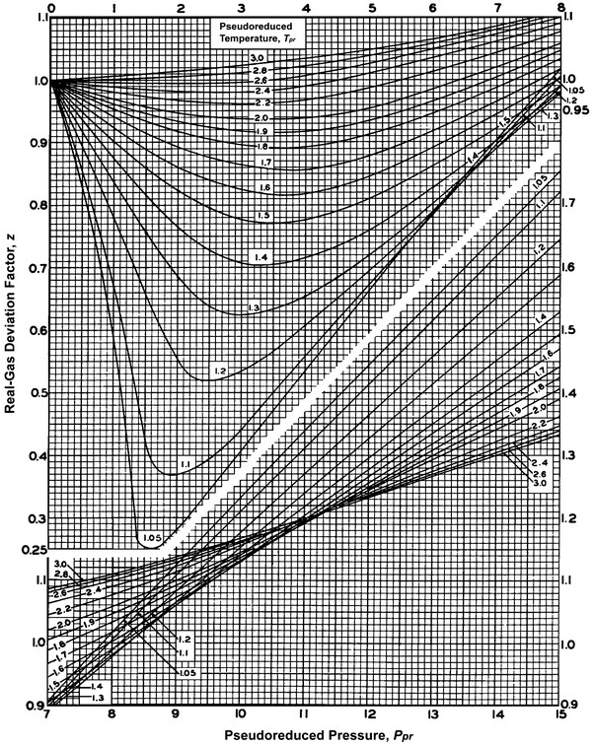
In cases where significant concentrations of inorganic impurities, CO2 and H2S are present, then corrections to Equation 3.61 and Equation 3.61 are required:
and
with
Where:
- ppc corrected is the corrected pseudo-critical pressure, psi
- ppc Eq. 3.61 is the pseudo-critical pressure from Equation 3.61, psi
- Tpc corrected is the corrected pseudo-critical temperature, °R
- Tpc Eq. 3.60 is the corrected pseudo-critical from Equation 3.60, °R
- ϵcorrection is the correction for CO2 and H2S, °R
- yCO2 is the mole fraction of CO2 in the gas phase, fraction
- yH2S is the mole fraction of H2S in the gas phase, fraction
The Standing-Katz[12] correlation has also been mathematically curve fit[13]. The equation for z-factor then becomes:
with
It should be noted that the solution of this equation for the z-factor requires an iteration procedure. This is because the z-factor appears both on the left-hand side of Equation 3.66 and the right-hand side of the equation through the pseudo-reduced density, ρpr. Typically, this is solved with a Newton-Raphson iteration procedure which is beyond the scope of this class. For our purposes, if supercompressibility factors are required, we can simply read the chart to obtain them.
Real Gas Formation Volume Factor, Bg
The Formation Volume Factor, Bg, of a real gas, like its oil phase analog, is used to convert one standard cubic foot, SCF, of gas at reference conditions to its volume at reservoir conditions. For natural gases, in the U.S. domestic oil and gas industry, we use the standard conditions of pSC = 14.7 psi and 60 °F. The gas formation volume factor for a real gas can be calculated directly from the Real Gas Law once we have an estimate of the super-compressibility factor. If we assume one lb-mole of natural gas, then the volume that it would occupy at standard conditions would be (assuming ZSC = 1.0 at standard conditions – a very good assumption):
At reservoir conditions, that same lb-mole would occupy a volume of:
Now, the gas phase formation volume factor we can define as:
There are times when we would like to consider the volume of gas in reservoir barrels, bbl. This is because we have used reservoir barrels as the units for the liquid (oil and water) volumes, and we would like to determine the volume occupied by the gas and liquids combined. We can convert the units of Equation 3.68a by applying the unit conversion constant of 1 bbl = 5.615 ft3:
Where:
- Bg is the gas formation volume factor, ft3/SCF (Equation 3.68a) or bbl/SCF (Equation 3.68b)
- Z is the supercompressibility factor at reservoir conditions, pr and Tr, dimensionless
- Tr is the reservoir temperature, °R
- TSC is the reference (standard) temperature (520 °R in U.S. domestic industry), °R
- pr is the reservoir pressure, psi
- pSC is the reference (standard) pressure (14.7 psi in the U.S. domestic industry), psi
Real Gas Compressibility, cg
The isothermal compressibility of a real gas can also be determined directly from the Real Gas Law. Starting with the definition of isothermal compressibility:
Substituting the Real Gas Law, Equation 3.27, into Equation 3.69:
or
The derivative, , can be calculated by differentiating Equation 3.66 and Equation 3.67 with respect to pressure.
Real Gas Density, ρg
The density of a real gas can also be determined directly from the Real Gas Law. Starting with the Real Gas Law:
Now the number of moles is equal to a mass divided by the molecular weight, n = m / MWg. Substituting into the Real Gas Law:
Now from the definition of gas density and the substitution of the Real Gas Law:
Where:
- ρg is the gas density, lb/ft3
- p is the pressure of interest, psi
- MWg is the molecular weight of the gas, lb/lb-mole
- Z is the supercompressibility factor at reservoir conditions, pr and Tr, dimensionless
- R is the Gas Constant, 10.73 ft3 psi / °R lb-mole
- T is the temperature of interest, °R
Real Gas Specific Gravity, γg
The specific gravity of a real gas can also be determined directly from the Real Gas Law. For gases, the specific gravity is defined as the ratio of the density of the gas to the density of air at standard conditions. Dividing Equation 3.71 written for a gas by Equation 3.71 written for air at standard conditions (Z = 1.0) results in:
Now, the molecular weight of gas is 28.87 lb/lb-mole:
Real Gas Viscosity, μg.
The viscosity of natural gases can be determined by the correlation of Lee, Gonzalez, and Eakin[14]:
with
Where:
- μg is the gas viscosity, cp
- K, X, and Y are correlation coefficients
- ρg is the gas density at the pressure and temperature of interest, gm/cc
- MWg is the molecular weight of the gas, lb/lb-mole
- T is the temperature of interest, °R
[12] Standing, M.B. and Katz, D.L.: "Density of Natural Gases," Trans., AIME (1942) 146, 140-49.
[13] Dranchuk, P.M. and Abou-Kassem, J.H.: "Calculations of z-Factors for Natural Gases Using Equations of State," J. Cdn. Pet. Tech. (July-Sept. 1975) 34-36.
[14] Lee, A.L., Gonzalez, M.H., and Eakin, B.E.: "The Viscosity of Natural Gases," JPT (Aug. 1966) 997-1000; Trans., AIME (1966) 234.
3.4: Reservoir Rock - Fluid Interaction Properties
To this point in the lesson, we have discussed Rock Properties and Fluid Properties, but we must also discuss how the rock and different fluids interact. In other words, how does the rock interact with the fluids and how do the various fluids interact with each other? At the pore and capillary scales, these interactions occur through the various attractive and repulsive forces acting on each component in the system (rock and fluids). These pore-scale forces include capillary forces, surface tensions, interfacial tensions, van der Waal forces, etc. While these topics are interesting in their own right, as engineers, we are interested in how these pore and capillary scale forces manifest themselves at a much larger macro-scale.
Phase Saturations, So, Sg, and Sw
To start the discussion about rock-fluid interaction properties, we must first define the phase saturations, So, Sg, and Sw, in the reservoir. The phase saturation is defined as the fraction of the pore volume occupied by a particular phase. For example, if the pore-volume of a porous medium by 65 percent oil, 25 percent gas, and 10 percent water, then the phase saturations would be:
- So = 0.65
- Sg = 0.25
- Sw = 0.10
Thus, if we had a core sample of rock with a bulk volume, Vb = 200.0 cc, an effective porosity, ϕ = 0.22, and the phase saturations listed above, then the core sample would contain:
- Vo=So Vp=SoϕVb = (0.65)(0.22)(200.0 cc) = 28.6 cc of oil
- Vg=Sg Vp=SgϕVb = (0.25)(0.22)(200.0 cc) = 11.0 cc of gas
- Vw=Sw Vp=SwϕVb = (0.10)(0.22)(200.0 cc) = 4.4 cc of water
where Vo, Vg, and Vw are the volumes of oil, gas, and water, respectively, in the core sample. By definition, the phase saturations must always sum to 1.0:
This relationship is known as the Saturation Constraint.
Capillary Pressure, pcow and pcgo
It has been observed that when two or more immiscible fluids occupy the pore-volume and capillaries of a porous medium, the pressures of the different phases are not equal, but are different from each other. This macro-scale phenomenon, known as capillary pressure, is due to interactions of the surface and interfacial tensions of the rock and fluids in the confined dimensions of the rock pores and capillaries. A force balance on the surface and interfacial tensions require that the pressures of the various phases are different. At the macro-scale, this phenomenon is quantified with the Capillary Pressure Relationships:
and
As shown in Equation 3.77 and Equation 3.78, the capillary pressure is the difference between the two phase pressures and is a function of the phase saturations. As written, these equations assume that the reservoir rock is Water Wetting Surface (the surface of the rock preferentially favors contact with the water phase). If we were to write these equations for an Oil Wetting Surface (the surface of the rock preferentially favors contact with the oil phase), then we would have:
and
We will not go into the details of Wettability, Water Wetting Surfaces, or Oil Wetting Surfaces; however, water wet reservoirs are the more common for petroleum rocks, and we will focus on them (Equation 3.77 and Equation 3.78). Please note that while water wetting rocks are the more common for reservoir rock lithologies, there are many examples of oil wet rocks in the petroleum literature. Figure 3.13 shows a typical drainage capillary pressure relationship for a water wet rock.
In Figure 3.13, the solid line is the drainage capillary pressure curve for a wetting phase (in our case, water in a water-wet rock). The capillary pressure, pe, is the Entry Pressure which is the pressure that is required to force a non-wetting phase (in our case, oil in a water-wet rock). The entry pressure is the pressure that is required to force the first drop of oil into the water-wet rock. Remember, the term “water-wet” implies that the rock has a preference to stay in contact with water. The entry pressure is the pressure required to overcome this preference. At some value of water saturation, the capillary pressure measurements begin to go asymptotic to the vertical. This water saturation, Swir, is the Irreducible Water Saturation and represents the minimum water saturation that the reservoir rock can reach in the presence of an oil phase. As indicated in this figure, irreducible water saturation is caused by capillary forces acting on the oil, water, and rock components of the system.

In this figure, the term “Drainage Capillary Pressure” appears; this refers to the manner in which the data were measured. There are two ways that we can measure capillary pressure. We could first fill the core sample with the wetting phase (in our case, water) and measure the capillary pressure by increasing the saturation of the non-wetting phase (in our case oil). This is identical to decreasing the saturation of the wetting-phase. This process, where the wetting phase saturation is decreased, is referred to as a Drainage Process and represents processes where the wetting phase is allowed to “drain” from the rock.
Alternatively, we could have first filled the core sample with the non-wetting phase (in our case, oil) and measured the capillary pressure by increasing the saturation of the wetting phase (in our case, water). This process, where the wetting phase saturation is increased, is referred to as an Imbibition Process and represents processes where the wetting phase is allowed to “imbibe” into the core. Both processes, drainage processes and imbibition processes, occur in oil and gas reservoirs.
It turns out that when you conduct the experiment using these two processes, you get different results. When this phenomenon occurs (measurements are dependent on the saturation history – increasing or decreasing wetting phase saturation), it is referred to as Hysteresis. Typical results for oil-water drainage and imbibition capillary pressure measurements including the impact of hysteresis are shown in Figure 3.14.
In Figure 3.14, we see that as we increase the saturation during an imbibition measurement cycle, the water saturation reaches an asymptotic maximum value, Sw max (or, 1 - Sorw). This trapped oil saturation, Sorw, is called the Residual Oil Saturation to Water and is the result of capillary forces occurring in the reservoir rock. We will discuss these end-point saturations, Swir and Sorw, in more detail when we discuss relative permeabilities.
While both drainage processes and imbibition processes occur in the reservoir, the topic of hysteresis is beyond the scope of this course. For this course, we will focus on the drainage capillary pressure of water wet reservoirs.

In the laboratory, capillary pressures are measured using Special Core Analysis (also known as SCAL) methods and must be specifically requested from the core laboratory. The drainage capillary pressure curves (Figure 3.13 and green curve in Figure 3.14) can be estimated from the Brooks-Corey Model[15]:
Where:
- pcow is the oil-water capillary pressure, psi
- λ is the pore-size distribution, dimensionless
- po and pw are the pressures of the oil phase and water phase, respectively, psi
- pe is the entry pressure, psi
- Sw is the water (wetting) phase saturation, fraction
- Swir is the irreducible water saturation, fraction
In the Brooks-Corey Model[15], λ, Swir, and pe can be obtained from the capillary pressure data. In addition, Swir can be obtained from open-hole well logs or by relative permeability data.
Relative Permeability, krow and krw
We have already discussed Darcy’s Law in the context of single-phase flow and absolute permeability. Darcy’s Law, Equation 3.24, was written earlier as:
Where qf is the volumetric flow rate in bbl/day, and all of the properties used in Equation 3.24 were discussed earlier. Note that we can convert the units of flow rate in Darcy’s Law from bbl/day to STB/day by the inclusion of the formation volume factor of the flowing fluid, Bf:
One of the assumptions listed with these versions of Darcy’s Law was that the flowing fluid is an incompressible, homogeneous, Newtonian fluid that fully saturates (single-phase) the porous medium. As we have already seen, the flow of fluids in real petroleum reservoirs is typically up to three-phase flow, and in some rare instances, may be as high as four-phase flow.
For multi-phase flow, we can rewrite Equation 3.82 for each of the phases present, regardless of whether the fluids are mobile or are stationary (we only care about their presence). Assuming three phases; oil, water, and gas, we have:
and
Note that we have assigned a phase designation to both the pressure, pf, and the permeability, kf. As discussed earlier, due to the capillary pressures, each of the phases present in the reservoir may have a different pressure, and consequently, we must distinguish between pressures (and pressure gradients) that are specific to each phase.
When we write a permeability value that is specific to an individual phase, kf, that permeability is referred to as the Effective Permeability to that phase. Therefore, in Equation 3.83, we have the effective permeability to oil, the effective permeability to water, and the effective permeability to gas (ko, kw, and kg, respectively).
The effective permeability is defined as the permeability to a specific phase in the presence of one or more other phases. These effective permeabilities, kf, are related to the absolute permeability, k, appearing in Equation 3.24 and Equation 3.82 through the Relative Permeability Relationships:
and
Where:
- kro, krw, and krg are the relative permeabilities to oil, water and gas, respectively, fraction
- k is absolute permeability (permeability for single-phase flow: Equation 3.24 and Equation 3.82), md
Substituting Equation 3.84 into these into Equation 3.83:
and
Relative permeabilities are functions of the phase saturations. A typical set of oil-water relative permeability curves is shown in Figure 3.15.
In Figure 3.15, the water saturation is plotted on the x-axis. The most important features that can be seen in this figure are the trends of the relative permeability curves. As the water saturation increase, the relative permeability to oil decreases while the relative permeability to water increases. This is because as the water saturation increases, fewer pathways become available for oil to flow while more pathways become available for water to flow.
In this figure, the parameters of irreducible water saturation, Swir, and residual oil saturation to water, Sorw, are identical to the values discussed earlier in the section on capillary pressure curves and shown in Figure 3.14. The water saturation range, Swir ≤ Sw ≤ 1 – Sorw, represents the range in which both the oil and water are mobile. Note that outside of this range, one of the relative permeability values is equal to zero, from Equation 3.85 a zero value of relative permeability implies that the flow rate will be zero.
On this plot, we can see that the maximum water saturation, Sw max = 1 – Sorw. We use this terminology because, as stated, the x-axis is the water saturation; while Sorw is an oil saturation. In other words, from Figure 3.15 we can see that Sorw is approximately 0.2, while due to the saturation constraint, ∑f=o,wSf = 1, Sw max must be 0.8.
For a two-phase, oil-gas system we have a somewhat similar set of relative permeability curves as with the two-phase, oil-water system. Figure 3.16 shows a typical set of gas-oil relative permeability curves.


In the gas-oil relative permeability curves, the gas saturation, Sg, is plotted on the x-axis. There are several important differences between the oil-gas system and the oil-water system that must be further discussed. One difference is the critical gas saturation, Sgc. The critical gas saturation is similar to Swir for water, in that it represents the value at which gas will begin to flow in situations the gas saturation is increasing (or, conversely, the saturation at which gas will stop flowing in situations the gas saturation is decreasing). We can also see oil is present and is mobile below Sgc (it has finite values below Sgc). This is because of the dissolved gas in the oil phase. As gas comes out of solution from a mobile oil phase, the gas saturation needs to build up to Sgc before it can begin to flow. While this is occurring, the oil phase remains mobile. Therefore, for gas-oil systems, oil is mobile in the range 0 ≤ Sg ≤ 1 – Sorg – Swir, and gas is mobile in the range Sgc ≤ Sg ≤ 1 – Sorg – Swir.
A second difference between the oil-water curves and the gas-oil curves is the use of the term krow in Figure 3.15 and the term krog in Figure 3.16. This is because the relative permeabilities to oil are different when measured in an oil-water system and in a gas-oil system. The is also true for the residual oil saturations, Sorw and Sorg. These differences are due to the differences in the surface tensions and resulting capillary forces between oil and water and between gas and oil.
A third difference is due to the irreducible water saturation, Swir. As we have already discussed, the irreducible water saturation is the lowest water saturation in the reservoir. Since all real oil and gas reservoirs contain water, the initial water saturation in these reservoirs, Swi, must be at least equal to the irreducible water saturation, Swir, or greater: Swi ≥ Swir. Therefore, to get representative laboratory measurements or calculations from correlations, we must include Swir in the analyses. Therefore, when we take laboratory measurements for gas-oil curves, we take them in the presence of an immobile, irreducible water saturation. Also note the application of the saturation constraint for the liquid (oil and water) saturations.
Relative permeability measurements also require special laboratory techniques and must be requested as a part of Special Core Analysis procedures when ordering tests from a core laboratory. There are two general approaches for laboratory measurements of relative permeability, the Unsteady State Method and the Steady State Method. Of the two methods, the Steady State Method (also known as the Penn State Method) is the more accurate laboratory procedure; however, it takes more time (and money) to perform these tests.
When laboratory data are not available, then the relative permeabilities can be calculated using a Power Law Model.
For oil-water curves, we have:
and
While for gas-oil systems we have:
and
Where:
- krow is the relative permeability to oil measured in an oil-water system, fraction
- krw is the relative permeability to water measured in an oil-water system, fraction
- krog is the relative permeability to oil measured in a gas-oil system in the presence of an irreducible water saturation, fraction
- krg is the relative permeability to gas measured in a gas-oil system in the presence of an irreducible water saturation, fraction
- krow(Swir) is the relative permeability to oil at the irreducible water saturation measured in an oil-water system, fraction
- krw(1 – Sorw) is the relative permeability to water at the maximum water saturation, measured in an oil-water system, fraction
- krog(Swir) is the relative permeability to oil at the irreducible water saturation measured in a gas-oil system in the presence of an irreducible water saturation, fraction
- krg(1 – Sliquid) is the relative permeability to gas at the maximum gas saturation, 1 – Sorg – Swir, in a gas-oil system in the presence of an irreducible water saturation, fraction
- So, Sw, and Sg are the oil, water, and gas saturations, respectively, fraction
- Swir is the irreducible water saturations, fraction
- Sorw is the residual oil saturation to a water displacement
- Sorg is the residual oil saturation to a gas displacement in a gas-oil system in the presence of an irreducible water saturation, fraction
- Sgc is the critical gas saturation where gas begins to flow in a gas-oil system in the presence of an irreducible water saturation, fraction
- now and nw are oil and water exponents, respectively, in an oil-water system (these exponents are referred to as Corey Exponents), dimensionless
- nog and ng are oil and gas exponents, respectively, in a gas-oil system in the presence of an irreducible water saturation (these exponents are also referred to as Corey Exponents), dimensionless
Most of these values can be seen in Figure 3.15 and Figure 3.16. Note that all of the groups in the parenthesis in Equation 3.86 through Equation 3.87 go from 0.0 to 1.0 in their respective mobile saturation ranges. These groups are often referred to as Normalized Saturations.
[15] Brooks, R.H. and Corey, A.T. 1964. Hydraulic Properties of Porous Media. Hydrology Paper No. 3, Colorado State University, Fort Collins, Colorado, 22–27.
3.5: Key Learnings
In this lesson, we discussed the following topics:
- The properties of interest to petroleum engineers are divided into three categories:
- Rock properties
- Fluid properties
- Rock-Fluid interaction properties
- These properties are most commonly used to improve our understanding of:
- Storage of oil, water, and gas in a petroleum reservoir
- Transport (movement) of oil, water, and gas in the reservoir
- The rock properties that we discussed included:
- Porosity (ability of a rock to store fluids)
- Compressibility (property of the rock that governs how volumes behave with changes in pressure)
- Permeability (ability of a rock to transmit fluids)
- Common methods used to determine porosity are:
- Laboratory measurements
- Grain determination by immersion
- Grain determination by Boyle’s Law
- Washburn-Bunting (mercury injection)
- Summation of fluids
- Well logs (field measurements):
- Sonic log
- Density log
- Neutron log
- Laboratory measurements
- Common methods used to determine permeability are:
- Laboratory measurements: Core Floods
- Field measurements:
- Well tests (or pressure transient analysis)
- Permeability-porosity cross-plots
- Fluid Properties:
- Formation volume factor: oil, gas, and water property that describes the reservoir volume occupied by one STB of liquid or one SCF of gas
- Compressibility: oil, gas, and water property that describes the change in volume with a change in pressure
- Viscosity: oil, gas, and water property that describes the ease with which a fluid can flow through a porous medium
- Density: oil, gas, and water property that quantifies the weight of a unit volume of fluid
- Specific gravity: oil, gas, and water property that normalizes the density to the density of a standard fluid – water for liquids and air for gases
- Bubble-point pressure: oil property describing the pressure that the first bubble of gas evolves from the oil with reducing pressures
- Solution Gas-Oil Ratio: oil property describing the amount of gas (in SCF) dissolved in one STB of oil
- Gas super-compressibility or real gas deviation factor: gas property that describes the deviation of a real gas from the ideal gas law
- API Gravity: oil property related to specific gravity
- Molecular weight: oil, gas, and water property that quantifies the weight of one mole of fluid molecules
- These properties (excluding molecular weight and specific gravity) are, in general, pressure dependent properties
- Rock-fluid interaction properties
- Phase saturation: oil, gas, and water property describing the fraction of the pore-volume occupied by the phase
- Capillary pressure: oil-water and gas-oil property that describes the difference in the pressures between the paired pressures
- Effective permeability: oil, gas, and water property that describes the permeability to one phase in the presence of one or more other phases in the porous medium
- Relative permeability: oil, gas, and water property that is the ratio of the effective permeability to a phase divided by the absolute permeability of the porous medium
- These properties are, in general, saturation dependent properties
3.6: Summary and Final Tasks
Summary
In this lesson, we learned that the two most critical considerations in petroleum engineering in general, and reservoir engineering, in particular, are the ability of the reservoir rock to store fluids and the ability of the reservoir rock to transmit fluids. We then learned that the properties that govern these two considerations can be divided into three categories: rock, fluid, and rock-fluid interaction properties. We also saw how properties within these categories need to be integrated to make meaningful analyses of subsurface phenomenon. For example, the multiphase version of Darcy’s Law, Equation 3-85, contains rock properties (permeability), fluid properties (viscosity and formation volume factor), and rock-fluid interaction properties (capillary pressure and relative permeability).
In addition, we discussed the data sources (field, laboratory, or derive from correlations) of the required data. We saw that there were multiple sources of reservoir properties. For rock properties, we saw that laboratory (core) and field measurements could be used (for example, core experiments and well logs for porosity determination and core floods and well tests for permeability determination).
For fluid properties, we saw that laboratory measurements (PVT cell) and property correlations could be used. We also saw that most of the fluid properties are pressure dependent.
Finally, we discussed the rock-fluid interaction properties. We started this discussion with an introduction to phase saturations and continued to discuss capillary pressures and relative permeabilities. We saw that the rock-fluid interaction properties were dependent on the phase saturations.
Final Tasks
Complete all of the Lesson 3 tasks!
You have reached the end of Lesson 3! Double-check the to-do list on the Lesson 3 Overview page [20] to make sure you have completed all of the activities listed there before you begin Lesson 4.
Lesson 4: Reservoir Engineering for Oil Reservoirs
4.0: Lesson Overview
Reservoir Engineering is the Petroleum Engineering Discipline which is concerned with the reservoir and oil accumulation oil as a whole. With the help of other petroleum professionals, such as drilling engineers, production engineers, and geologists, reservoir engineers attempt to optimize oil production from the reservoir or field in its entirety. Typical tasks performed by reservoir engineers working on oilfields include estimating the original oil-in-place, or STOOIP (Stock Tank Oil Originally In-Place), analyzing current production rate and pressure trends from the wells and the reservoir, forecasting future performance from these trends, and determining the Estimated Ultimate Recovery, or EUR, of a well, reservoir, or field.
There may be several methods available for performing the aforementioned tasks. Where multiple methods exist, we will discuss the more common methods available to the practicing reservoir engineer. In addition, we will discuss the assumptions inherent in each method.
Learning Objectives
By the end of this lesson, you should be able to:
- list some of the daily tasks performed by reservoir engineers;
- discuss two methods of calculating the Stock Tank Oil Originally in-Place, STOOIP, in an oil accumulation;
- calculate the STOOIP of a reservoir using the Volumetric Method and Material Balance Method;
- list and describe the five drive mechanisms associated with oil production given the proper data;
- list the major flow regimes experienced by vertical production wells;
- calculate the stabilized production rates from a production well given the current flow regime and given appropriate data;
- understand the concept of well damage or stimulation and know how to incorporate it into well production rate calculations;
- forecast future production from a reservoir or production well using the Material Balance Method and Decline Curve Analysis;
- list the three decline types considered by Arps Decline Curves;
- perform decline curve analysis using Arps Decline Curves; and
- understand the difference between economically recoverable oil and Estimated Ultimate Recovery (EUR).
Lesson 4 Checklist
| To Read | Read the Lesson 4 online material | Click the Introduction link below to continue reading the lesson 4 material |
|---|---|---|
| To Do | Lesson 4 Problem Set | Submit your solutions to the Lesson 4 Problem Set assignment in Canvas |
Please refer to the Calendar in Canvas for specific time frames and due dates.
Questions?
If you have questions, please feel free to post them to the Course Q&A Discussion Board in Canvas. While you are there, feel free to post your own responses if you, too, are able to help a classmate.
4.1: Introduction
In Lesson 3, we went over the basic rock, fluid, and rock-fluid interaction properties used by petroleum engineers on a daily basis. These form the building blocks for reservoir engineering calculations and forecasting procedures. In this lesson, we will discuss how these properties are used by reservoir engineers to predict how oil wells and oil fields behave.
For reservoir engineers, two main concerns are the estimation of the in-place fluids and the estimation of the rates and volumes of fluids produced from the production wells and from the field. For in-place fluid calculations, the Volumetric Method, which is based on static geological data, and the Material Balance Method, which is based on dynamic production and pressure data, are used. Both methods are commonly used in the oil and gas industry today.
For well performance, we will use Darcy’s Law in our analyses. In Lesson 3, we briefly discussed Darcy’s Law for fluid flow through porous media. The multi-phase version of Darcy’s Law (Equation 3.85), written for phase “ ” is:
Where is the pressure drop in the direction, which causes fluid flow. Darcy’s Law governs flow both at the well locations and in the interior of the reservoir. Consequently, this equation will be a fundamental tool for evaluating the performance of individual wells and the reservoir in its entirety.
Finally, we will discuss the application of material balance methods in the reservoir. Material balance is a tool used in many engineering disciplines; however, in this lesson, we will apply it to crude oil reservoirs. Put simply, material balance states that “matter can be neither created nor destroyed.” For our purposes, this implies that any change in mass in the reservoir must equal the mass being removed through the wells. As discussed earlier, material balance can be used for the estimation of the STOOIP (Stock Tank Oil Originally In-Place). In addition, it can be used for estimating the reservoir and field performance. We will discuss several material balance methods for crude oil reservoirs. In the next lesson, we will apply material balance to natural gas reservoirs.
4.2: Estimation of Stock Tank Oil Originally In-Place, STOOIP Using the Volumetric Method
As mentioned earlier, the Volumetric Method for STOOIP uses estimates of static geologic data to determine the volumes of the in-place fluids (crude oil, natural gas, and water). Static data are data which do not change with time due to oil and gas production. These static data are measured from core and log data.
For the volumetric method, the Gross Rock Volume (total rock volume of the reservoir zone of interest) and average values of porosity, fluid saturation, Net-to-Gross ratio (ratio of the volume of the productive reservoir to the total rock volume, i.e., the ratio of the volume of the reservoir that contributes to flow to the total rock volume), and the fluid formation volume factors ( ). While these properties can be determined on a point-by-point basis from core and log data at the well locations, development geologists use specialized geological modeling techniques to determine the inter-well properties and the averaged values of these properties.
By simply using the definition of reservoir volumes, the in-place volumes of the different reservoir fluids can be determined by:
Where:
- is the in-place volume of phase p, STB for crude oil and water or SCF for natural gas
- is the gross rock volume, ft3
- is the net-to-gross thickness ratio, fraction
- is the average net reservoir thickness, ft
- is the average gross reservoir thickness, ft
- is the average reservoir porosity, fraction
- is the average phase saturation, fraction
- is a unit conversion constant, 5.615 ft3/bbl for crude oil and water or 1.0 for natural gas
- is the average formation volume factor of phase , bbl/STB for crude oil and water or ft3/SCF for natural gas
In Equation 4.02, , is the average net thickness (the thickness of the reservoir that (1) contains hydrocarbons and (2) has sufficiently high permeability to contribute to flow), and is the average gross thickness (the total thickness of the reservoir). The net-to-gross ratio is simply the fraction that converts the total reservoir thickness to the thickness that contributes to hydrocarbon storage and flow in the reservoir. We can further define the gross rock volume as:
Where:
- is the gross rock volume, ft3
- 43,560 is a unit conversion constant, ft2/acre
- is the mapped area of the reservoir, acres
- is the average gross reservoir thickness, ft
Specifically, in standard SPE (Society of Petroleum Engineers) nomenclature, we have:
and
Where:
- 5.615 is a unit conversion constant, ft3/bbl
- is the Stock Tank Oil Originally In-Place (STOOIP), STB
- is the Original Gas In-Place (OGIP), SCF
- is the original water in-place, STB
Note that in Equation 4.04a, we used the saturation constraint, . To use the Volumetric Method to determine the Stock Tank Oil Originally In-Place, all of the pressure dependent properties are evaluated at the initial reservoir pressure, , as are all of the saturations, ,, and . All of the averages in these equations are averages over location (not averages over time).
The volumetric method for estimating the in-place volumes is considered to be less accurate than the material balance method. The reason for this is because of the use of all of the averages used in the volumetric method. This defect in the volumetric method can be improved by the use of an iso-contour parameter, . The iso-contour method calculates the composite property, , from the individual constituents:
The composite property, , is evaluated at the known at the points of Well Control (well locations where the properties , , , , and can be measured and are assumed to be known). Since the values that make up are all known at the points of well control, they can be used to evaluate without any averaging. Once values of are evaluated at the points of well control, they can then be averaged to determine . With the fluids in-place can be calculated with:
and
This approach reduces the averaging processes from the four averages required in Equation 4.04 to one required in Equation 4.06.
We will defer the discussion of the material balance method for the estimation of STOOIP until later in this lesson when we discuss field performance.
4.3: Drive Mechanisms in Oil Reservoirs
As with all gases and liquids in nature (weather fronts, sea and air currents, etc.), crude oil in the reservoir flows from locations of high pressure (the interior of the reservoir) to locations of low pressure (production wells). It is this pressure differential that is the driving force for fluid flow and production from wells. To start our discussion on fluid movement, we will begin with a discussion of the Drive Mechanisms in an oil reservoir. Drive mechanisms are the physical phenomena that occur in the reservoir that help to keep the reservoir pressures high.
There are five drive mechanisms that are associated with the Primary Production (production that occurs without any pressure maintenance supplied by fluid injection or by use of chemical, miscible, or thermal enhanced recovery methods) of a crude oil reservoir. These are:
Rock and fluid expansion occur due to the slightly compressible nature of crude oil, Interstitial (or Connate) Water, and reservoir rock. Interstitial, or connate, water is the initial water saturation in the reservoir at discovery. In Lesson 3, we saw that as pressure is reduced the compressibility of the rock and fluids (Equation 3.17, Equation 3.26, Equation 3.30, and Equation 3.43a) causes the volumes of the oil and water to expand and the pore-volume to shrink (equivalent to the rock grain volume expanding). All of these phenomena cause the pressure to remain higher than it would otherwise have been had they not been occurring (engineering analysis would indicate that if the fluids are expanding and the pore-volume is shrinking, then the in-situ fluids will be displaced to areas of low pressure).
We can think of rock and fluid expansion with the simple analogy of a water (or oil) filled balloon. If we fill the balloon with water, then the size of the balloon increases due to the increased pressure required to force the water into the balloon. In addition, if we pinch down on the balloon opening, then the water would remain in place inside of the balloon. In this example, the pore-volume in the reservoir is analogous to the water filled space in the balloon and the in-place fluid is the high-pressure water. Now, if we were to release the balloon opening to the low pressure atmosphere, then the pore-volume in the balloon would shrink and, to a lesser extent, the water inside the balloon would increase. These two effects cause the water to flow out of the balloon to the atmosphere. One conceptual issue with this analogy is the highly compressible nature of the rubber balloon. In a reservoir, the rock grains are many orders of magnitude less than the compressibility of rubber. Consequently, the flow of fluids from a hydrocarbon reservoir will not be as dramatic as that presented in this example.
Rock and fluid expansion occurs in most reservoirs; however, due to the small changes in volume associated with the slightly compressible nature of oil and water, and the low compressibilities associated with most reservoir rock, this drive mechanism has a very low recovery efficiency and typically accounts for less than five percent recovery of the STOOIP. In addition, in the presence of a free gas phase, its impact is dwarfed by the highly compressible nature of gas (note: gas expansion is excluded from rock and fluid expansion drive because the expansion of gas is included as separate drive mechanisms in solution gas drive and gas cap drive). Consequently, rock and fluid expansion may only be significant in undersaturated crude oil reservoirs (oil reservoirs discovered at pressures above the bubble-point pressure of the crude oil, .
Solution gas drive is caused by the solubility of natural gases in crude oils. This was discussed in Lesson 3 and is quantified with the oil property of the solution gas-oil ratio, . In undersaturated oil reservoirs, oil is found as a single-phase hydrocarbon fluid at discovery. As wells are drilled and put into production, the reservoir pressure declines (but supported by rock and fluid expansion) until it reaches the bubble-point pressure. At this time, gas comes out of solution and also begins to expand. It is the expansion of the gas that was originally in solution in the oil phase that we refer to as solution gas drive.
An analogy that we can use for solution gas drive is a bottle full of a carbonated beverage. If we were to shake a bottle of carbonated beverage with our thumb covering the bottle opening, the beverage would remain in the bottle. Now, if we were to remove our thumb from the bottle opening, then the gas in the beverage would come out of solution and expand in the bottle. This expansion of the liberated gas would drive both the beverage (and any gas remaining in solution in the beverage) and the free gas out of the bottle.
Typically, solution gas drive accounts for between 15 – 20 percent recovery of the STOOIP in normal oil reservoirs.
Gas cap drive is similar to solution gas drive; however, it only occurs in saturated oil reservoirs (oil reservoirs discovered below the bubble-point pressure of the crude oil). In saturated oil reservoirs, the free gas forms a Gas Cap (portion of the reservoir overlain by free gas due to gravity segregation). For example, the red colored region of the Numbi field in Figure 3.01 [21] is a gas cap. As wells are drilled and put into production, the pressure declines (again, other drive mechanisms may provide support to partially maintain the reservoir pressure), and the gas cap begins to expand. It is the expansion of the gas that was originally free in the reservoir that we refer to as gas cap drive.
Please note that during pressure decline, gas will also come out of solution. The expansion of this liberated gas is still referred to as solution gas drive. Thus, in this situation, we would have combined drives occurring simultaneously in the reservoir including gas cap drive and solution gas drive, and, to a lesser extent, rock and fluid expansion.
Gas cap drive can account for up to 30 percent recovery of the STOOIP depending on the size of the original gas cap.
Gravity drainage is another drive mechanism that can occur in both saturated and undersaturated oil reservoirs. In very thick reservoirs or in highly dipping reservoirs, gravity drainage can be a very effective drive mechanism and may account for up to 40 percent recovery of the STOOIP. In order to be effective, wells must be completed deep in the reservoir and must have a large Oil Column (reservoir depth containing oil) above the completion.
The last drive mechanism associated with oil reservoirs is aquifer drive, or water encroachment. If a reservoir is in contact with a water-bearing aquifer, then as the reservoir pressure declines, the rock and water in the aquifer expand and water is expelled from the aquifer and into the reservoir. This encroachment of water into the reservoir provides pressure support and helps to displace oil from the regions of the reservoir in contact with the aquifer to production wells. Aquifer drive may account for 35 – 45 percent recovery of the STOOIP depending on the size of the aquifer.
As previously discussed, these drive mechanisms commonly act simultaneously. When this occurs, we refer to the reservoir as a reservoir undergoing combined drive. Table 4.01 shows the drive mechanisms typically found in crude oil reservoirs and the maximum Recovery Factors (percentage of STOOIP recovered) typically observed in the field.
| Recovery Mechanism | Typical Recovery Efficiencies (Percent STOOIP) |
|---|---|
| Rock and Fluid Expansion | Up to 5 percent |
| Solution Gas Drive | 20 |
| Gas Cap Drive | 30 |
| Gravity Drainage | 40 |
| Aquifer Drive (Weak Aquifer) | 35 |
| Aquifer Drive (Strong Aquifer) | 45 |
| Combined Drive Mechanisms | 60 – very rarely this high |
The recovery factors shown in Table 4.01 may be a little deceptive since they represent the maximum recovery factors that can be expected from the reservoir for the different drive mechanisms. Typically, overall (combined) recovery factors from primary production rarely exceed 30 – 35 percent recovery of the STOOIP of the reservoir.
4.4: Performance of Oil Wells
4.4: Performance of Oil Wells section of this lesson will cover the following topics:
- 4.4.1: Stabilized Performance of Oil Wells [22]
- 4.4.1.1: Steady-State Flow of Oil to a Vertical Production Well with No Well Damage or Well Stimulation [23]
- 4.4.1.2: Steady-State Flow of Oil to a Vertical Production Well with Well Damage or Well Stimulation [24]
- 4.4.1.3: Steady-State Flow of Oil to a Vertical Production Well in Terms of the Average Pressure [25]
- 4.4.1.4: Pseudo Steady-State Flow of Oil to a Vertical Production well [26]
- 4.4.1.5: Inflow Performance Relationship for Stabilized Flow to an Oil Production Well [27]
- 4.4.2: Transient Performance of Oil Wells [28]
Note: You can access specific subsections of the lesson by clicking on the links above or continue reading through the lesson using the link below.
4.4.1: Stabilized Performance of Oil Wells
4.4.1: Stabilized Performance of Oil Wells section of this lesson will cover the following topics:
- 4.4.1.1: Steady-State Flow of Oil to a Vertical Production Well with No Well Damage or Well Stimulation [23]
- 4.4.1.2: Steady-State Flow of Oil to a Vertical Production Well with Well Damage or Well Stimulation [24]
- 4.4.1.3: Steady-State Flow of Oil to a Vertical Production Well in Terms of the Average Pressure [25]
- 4.4.1.4: Pseudo Steady-State Flow of Oil to a Vertical Production well [26]
- 4.4.1.5: Inflow Performance Relationship for Stabilized Flow to an Oil Production Well [27]
Note: You can access specific sections by clicking on the links above or continue reading through the lesson using the link below.
4.4.1.1: Steady-State Flow of Oil to a Vertical Production Well with No Well Damage or Well Stimulation
As stated earlier, the flow of oil to a production well is governed by Darcy’s Law. In this section, well damage is defined as a near-well permeability reduction (non-geological) caused by drilling or production. We will start our discussion by assuming that steady-state conditions prevail for the system. While steady-state conditions seldom occur in actual reservoirs, the analysis of production wells under these conditions forms the basis of the analysis methods of wells under more common reservoir conditions (pseudo steady-state conditions or transient, time-dependent conditions).
For steady-state analysis, we need to make the following assumptions:
- Flow is steady-state and Darcy’s Law applies and all of the inherent assumptions of Darcy’s Law are valid in the system.
- The drainage volume is radial-cylindrical (see Figure 4.01).
- The drainage volume is bounded in the interior with a cylindrical well (radius equal to ) and kept at flowing well pressure of
- The drainage volume is bounded on the exterior with a cylindrical boundary (radius equal to ) which has an external pressure of ( < )
- The drainage volume is bounded on the top and bottom (constant height) no-flow boundaries.
- Within the drainage volume the rock properties are homogeneous (uniform with location).
- Within the drainage volume the rock properties are isotropic (uniform in all directions).
- Flow is horizontal.
With these assumptions, we can use the single-phase version of Darcy’s Law:
Now, for radial flow, we have:
Substituting into Darcy’s Law, we have:
The purpose of the negative sign in Equation 4.07 now becomes apparent: for a positive pressure gradient (pressure increasing with radius), flow is in the negative r-direction (flow is inward to the well: note direction of radii in Figure 4.01). Separating variables and integrating results in:
Now, using the assumption of a homogeneous permeability (constant with respect to location) and slightly compressible fluid (approximately constant , , and ), we have:

Performing the integration results in Equation 4.12 results in:
or,
Rearranging Equation 4.14 results in:
Equation 4.15 describes the steady-state flow of a single-phase, incompressible or slightly compressible fluid to a well in a radial-cylindrical drainage volume.
4.4.1.2: Steady-State Flow of Oil to a Vertical Production Well with Well Damage or Well Stimulation
During drilling operations, filtrate from the drilling fluid can seep into the reservoir, causing several potential problems including swelling of clays, resulting in a restriction of pores causing a thin zone of absolute permeability degradation near the wellbore, and the formation of a two-phase zone, resulting in effective permeability impairment due to the impact of relative permeability near the well. In addition, fluid production may cause Fines Movement (movement of loose rock materials and debris) from the reservoir interior towards the well. Finally, the well may also be Stimulated (near well increase in permeability) by the use of a Hydraulic Fracturing Treatment or an Acid Stimulation Treatment.
This well damage or stimulation is introduced into the analyses with a Skin Factor (local, near-wellbore adjustment to the pressure drop – reduced or increased – due to permeability modification for reasons other than geological reasons). This damage or stimulation is called a “skin” factor because it results in a relatively small zone of increased pressure-drop (or increase) near the well. This skin zone is illustrated in Figure 4.02 as the light green zone adjacent to the well.

In reservoir Engineering, we quantify this additional pressure drop in the skin zone by use of a dimensionless parameter, . From Equation 4.14, we have:
By inspection, we can see that the left-hand side of this equation is dimensionless which implies that the right-hand side must also be dimensionless. Therefore, we can add our dimensionless skin factor, , to the left-hand side of the equation:
By doing this, in order to maintain the equality, we have either (1) modified the pressure drop, , if the production rate, , is fixed or, (2) modified the production rate if the pressure drop is fixed. Rearranging Equation 4.17 to the form of Equation 4.15 results in:
Well damage will occur if the permeability in the skin zone is less than the natural permeability of the reservoir, while stimulation will occur if the permeability in the skin zone is greater than the natural permeability of the reservoir. From Equation 4.18, we can see that if the skin factor, , is positive, then it results in a reduction in the production rate if the pressure drop is fixed. Therefore, a positive skin factor is an indication of damage to the well. On the other hand, a negative value of skin factor results in an increase in the production rate if the pressure drop is fixed. Therefore, a negative value of the skin factor is an indication of stimulation to the well.
In the field, the skin factor can be determined from a pressure transient test, such as a pressure build-up test. In Lesson 3, we described a pressure build-up test and its analysis tool, the Horner Plot (see Figure 3.05). For convenience, this figure has been copied from Lesson 3 and is shown as Figure 4.03.
In that lesson, we discussed the Horner Plot in the context of field measurements of reservoir permeability. In that discussion, we saw that if we first produced a well at a stabilized rate, , for a certain period of time, , (the stabilized production time) and followed this by shutting in the well, then we could estimate the effective permeability to oil in the reservoir, , by the way that the shut-in pressures, , Built-Up (increased) over time. We quantified our analyses using the resulting Horner Plot:
Where:
Where:
- is the effective permeability to oil, md
- 162.6 is an equation constant
- is the oil production rate during the stabilized production period, STB/day
- is the oil viscosity, cp
- is the oil phase formation volume factor, bbl.STB
- is the slope of the Horner plot, in psi/cycle
- is the thickness of the reservoir, ft
- is the shut-in well pressure estimated from the linear portion of the plot, psi
Remember, as we discussed in Lesson 3, the effective permeability is the product of the relative permeability to oil and the absolute permeability of the rock formation:
We need to keep the relative permeability in our field calculations because all reservoirs will contain a water saturation (at the minimum it will be the irreducible water saturation, ). In addition to the effective permeability to oil, we can also determine the skin factor from the well test. For an arbitrary shut-in time increment, , the skin factor can be calculated from:
By convention, the time used in the skin analysis is normally taken to be one hour: . Substituting into Equation 4.22a:
Where:
- 1.1513 and 3.2275 are equation constants
- is the slope of the linear portion of the Horner plot, psi/cycle
- is the shut-in well pressure after 1 hr estimated from the linear portion of the Horner plot (see Figure 4.03), psi
- is the last measured flowing pressure during the stabilized production period ( at , i.e., ), psi
- is the total time duration of the stabilized production period, hrs
- is the time increment from the start of the well shut-in period, hrs
- is the effective permeability to oil, md
- is the porosity of the reservoir, fraction
- is oil viscosity, cp
- is total compressibility of the system, 1/psi
- is the well radius, ft
We can further simplify Equation 4.22b in cases where . In these cases, the expression in the first logarithmic term, , causing this term to vanish: remember, . In these cases, Equation 4.22b becomes:
When reservoir or production engineers design a pressure build-up test, they normally design it so that this approximation is valid. We can see from Equation 4.22, that in order to estimate the skin factor, we must first estimate the effective permeability, , and slope, , from Equation 4.19 and Equation 4.20.
You will notice that I use the term “estimate” when I discuss the application of these field methods for the determination of reservoir or well properties as opposed to “calculate”; this is intentional. While Equation 4.19 through Equation 4.22 are theoretically sound equations, (1) all of the properties used in them (, , , , , , , , , and ), to some degree have measurement error associated with them, and (2) many of the assumptions used in the equation development (uniform thickness, uniform permeability, etc.) may not be strictly applicable to our reservoir.

4.4.1.3: Steady-State Flow of Oil to a Vertical Production Well in Terms of the Average Pressure
In our earlier discussions, we used the pressure drop from the external radius, at to determine the production rate, . In many situations, we may not know the reservoir pressure at ; however, we may know the average reservoir pressure, . In fact, as we will see during our discussion on material balance, this is actually the more common situation. This situation is depicted in Figure 4.04, where the pressure at the external radius, has been replaced with the average pressure, , in the interior of the drainage volume.
We can also develop equations for production rate for cases where we only know . To do this, we start with Equation 4.12. Rather than integrating this equation from to , we can change the limits of integration from to an arbitrary radius, , and the corresponding pressure at this radius, :
This results in an equation similar to Equation 4.14, but incorporating the arbitrary integration limits:
Solving for the pressure, , results in:
Equation 4.25 describes the Pressure Distribution (pressure as a function of location, which in our case is the pressure as a function radius) in the drainage volume. As one would expect, this equation indicates that as the radius, , increases away from the production well, the pressure also increases (i.e., fluids are flowing from regions of high pressure to the region of low pressure, the production well). The volumetric average of any property, (where upper case “” is any point-by-point property), can be calculated from:

Now, the volume of a cylinder is defined as:
Differentiating Equation 4.27 with respect to volume assuming a uniform thickness, , results in:
Substituting Equation 4.27 and Equation 4.28 into Equation 4.26 yields:
Now, substituting Equation 4.25 into Equation 4.29:
Performing the integration yields:
or,
or,
If we assume that , then . This is a very good assumption because the radius of the drainage volume of a well is typically on the order of hundreds or thousands of feet while the radius of the well is normally less than one foot. Using this approximation, Equation 4.31c becomes:
or, after rearranging:
Using the same methodology discussed earlier, we can also introduce the skin factor, , to account for well damage or stimulation:
Equation 4.34 is the relationship between the production rate of a liquid, , and the average reservoir pressure, . This equation has a similar form to that of Equation 4.19, but with two notable differences:
- The factor of ½ in the denominator of Equation 4.34
- The use of the average reservoir pressure in the drainage volume, , the pressure drop calculation in Equation 4.34
As I mentioned earlier, the use of, , has important consequences when applying material balance methods. We will discuss this later in this lesson.
4.4.1.4: Pseudo Steady-State Flow of Oil to a Vertical Production well
In all of our discussions on well performance, we assumed that Steady-State Conditions (time-invariant conditions) were occurring in the reservoir. Steady-state implies that nothing changes in the drainage volume with time or production. This simplification is not appropriate for most real production situations. Figure 4.05 shows the more common Transient Flow Conditions (time-dependent conditions) that occurs in the reservoir.

In this figure, the early-time pressures (green curves) form a pressure disturbance that over time propagates outward toward the external radius of the drainage volume, . At some point in time, this pressure disturbance reaches the external boundary (bold red curve). This time is referred to as the time to pseudo steady-state, . Pseudo steady-state is a flow regime which is defined by a uniform pressure drop from one time to the next, , that is equal everywhere in the drainage volume. This is illustrated in Figure 4.05 by the blue curves. The solid dual-headed arrows indicate that the pressure drop is the same at each radius in the reservoir.
The transient behavior of a radial-cylindrical drainage volume with uniform (constant) reservoir properties is governed by the partial differential equation (diffusivity equation):
I will derive this equation later in the lesson when we discuss fully transient flow; however, for the time being, we will consider its use in the context of pseudo steady-state flow. Without going into the details, the solution to this equation at times greater than can be approximated by:
Where:
- 5.615 is a unit conversion constant, ft3/bbl
- 1.127x10-3, 141.22, and 0.012648 are equation constants
- is the flowing well pressure, psi
- is the initial reservoir pressure, psi
- is viscosity, cp
- is the formation volume factor, bbl/STB
- is the liquid rate in STB/day
- is the permeability, md
- is the reservoir thickness, ft
- is the time, days
- is the porosity of the reservoir, fraction
- is total compressibility of the system, 1/psi
- is the external radius of the drainage volume, ft
- is the well radius, ft
Now, for slightly compressible liquids, we can calculate the average reservoir pressure by using the definition of compressibility:
In Equation 4.37, we set equal to the volume produced from the well over the time period , , and equal to the pore volume of the drainage volume in ft3. Substituting from Equation 4.37 into Equation 4.36 results in:
If we again assume that , then and the two time-dependent terms, , cancel. This results in:
Using the same methodology discussed earlier, we can also include the skin factor, , to account for well damage or stimulation:
We should not be surprised that the time dependent terms in Equation 4.38 canceled because during the pseudo steady-state flow regime, the pressure drop, , is uniform everywhere (see Figure 4.05). Thus, once the pressure distribution is formed at (red curve in Figure 4.05), the shape of the curve must remain intact throughout the remainder of the productive life of the well (assuming no changes in the production rate, ). The downward shift in the curves shown in Figure 4.05 are due to the reduction in the average reservoir pressure, , during pressure depletion.
4.4.1.5: Inflow Performance Relationship for Stabilized Flow to an Oil Production Well
The well performance equations that we have discussed to this point; Equation 4.18, Equation 4.34, and Equation 4.40; are known collectively as the well Inflow Performance Relationships, IPR (relationship between the flowing well pressure, , and the production rate, , from the well). Table 4.02 summarizes the flow regimes and the IPR equations.
| Steady-State Flow Regime | Pseudo Steady-State Flow Regime | |
|---|---|---|
| Pressure Distribution | ||
| In terms of at the external radius, , of the drainage volume | ||
| Drawdown | ||
| Productivity Index |
||
| IPR | ||
| In terms of in the interior of the drainage volume | ||
| Drawdown | ||
| Productivity Index |
||
| IPR | ||
| [A] Note, we did derive the equations in the shaded cells, but they are included for future reference. | ||
In Table 4.02, I introduced some new terminology. The pressure drop in these equations, , is referred to as the Drawdown or the Drawdown Pressure; while the term multiplying the drawdown is the referred to as Productivity Index, PI (sometimes the productivity index is also referred to by the symbol ). The oilfield units of the drawdown are psi; while the oilfield units of the productivity index are STB/(day psi).
Using this terminology, we can simplify the Inflow Performance Relationship to:
Where the appropriate definitions for the drawdown and productivity index are selected from Table 4.02 given the prevailing reservoir conditions (flow regime). Equation 4.41 is very useful for practical applications. In the field, we can change the well flowing pressure, , by changing the choke size on the well and measure the resulting stabilized production rate, . By doing this several times, we can estimate the productivity index from:
To do this, we must have some knowledge of the field pressure, typically measured by shutting in the well of interest or by shutting in Offset Wells (adjacent wells). Using this approach, the productivity of the well can be established without the need of knowing the individual well properties (, , , etc.) or the flow regime (steady-state or pseudo steady-state). The measured drawdowns and production rates provide the appropriate productivity index to allow for future well calculations.
In fact, we can use the field measured productivity indices even in cases with mixed flow boundaries/regimes. For example, we may have a situation where a strong aquifer is located south of a production well which keeps the southern external boundary of the drainage area nearly constant (steady-state). While north of this production well, pressure depletion may be occurring due to production from offset wells. In this situation, we do not need to make any assumptions regarding the flow regime, which best describes the well or what definitions of drawdown or productivity index we need to use. If we do the field measurement, then the test will provide the correct results for that specific well.
4.4.2: Transient Performance of Oil Wells
In our earlier discussions, we assumed that the well had produced for sufficient time to allow the pressures and production rates to stabilize. Transient Flow (time-dependent flow) describes the full time-dependence of these pressures and rates. If we were to produce a well at a constant rate, , then the flowing well pressure, , would behave as illustrated in Figure 4.06 on the following page.
4.4.2.1: Flow Regimes during Transient Flow
In Figure 4.06, the flowing well pressures, , are plotted as a function of time for a constant production rate. These flowing well pressures are the points, “•”, plotted in Figure 4.05. In this figure, several flow regimes are illustrated; some we have already discussed; others we have not.
For early times (solid red curve), the well pressure response is dominated well damage, well storage, or both. We have already discussed well damage earlier in this lesson. Well storage is the pressure response due to the liquids and gas in the well itself. Because the liquids are slightly compressible, and the gas is compressible, the flowing pressure of the well, , will be influenced by the compressibility of the fluids in the well.
The transient period (solid light green curve) in Figure 4.06 is flow regime that we are discussing in this subsection. The transient behavior of the well is described by the partial differential equation, Equation 4.30. The general solution to this equation forms the basis for Pressure Transient Analysis, PTA – such as the Pressure Build-Up Test and Horner Plot – that we discussed earlier.
The solid, dark green curve represents the late transient flow regime. As we have discussed, as a pressure disturbance caused by production travels through the reservoir, it will eventually encounter the boundaries of the drainage volume. For radial-cylindrical drainage areas in reservoirs with Homogeneous (uniform) and Isotropic (no directional preference) properties, this pressure disturbance comes into contact with all of the boundaries instantaneously (or at least over a short time interval).

For square drainage areas, the pressure disturbance will contact the edges of the boundary first followed by the corners. For rectangular drainage areas, the pressure disturbance would first contact the boundaries on the short side of the rectangle, followed by the boundaries on the long side of the rectangle, and finally the corners of the rectangle. Therefore, for shapes other than cylindrical, the time duration for the pressure disturbance to contact all of the drainage volume boundaries may be drawn out. The late transient period is then defined as the period for the pressure disturbance to contact the first boundary through the last boundary of the drainage volume.
The boundary dominated period is shown by the two blue curves in Figure 4.06 with the dashed blue curve representing the steady-state flow regime and the solid blue curve representing the pseudo steady-state regime. We have already discussed these two flow regimes in detail in this lesson.
4.4.2.2: Derivation of the Diffusivity Equation in Radial-Cylindrical Coordinates
The derivation of the diffusivity equation in radial-cylindrical coordinates will be the last topic in our discussion on individual well performance. It also gives us the opportunity to introduce the topic of material balance, as we will use this concept in the following derivation.
If we perform a mass balance on a thin ring or Representative Elemental Volume, REV, in the reservoir as shown in Figure 4.07, then we would have:
Equation 4.43 simply states that any mass entering the REV at its outer boundary less the mass exiting the REV at its inner boundary must be accumulating in the REV. We can elaborate on the definitions of terms in Equation 4.43 as:
and,
Where:
- 5.615 is a unit conversion constant, ft3/bbl
- is the liquid density, lb/ft3
- is the liquid rate, bbl/day
- is the radial coordinate in a radial-cylindrical coordinate system, ft
- is the radius of the representative elemental volume, REV, ft
- is time, days
- is the porosity of the reservoir, fraction
- REV is the bulk volume of the representative elemental volume, REV, ft3
- is the reservoir thickness, ft

Substituting Equation 4.44 through Equation 4.46 into Equation 4.43 results in:
or,
Dividing by the term results in:
Now, substituting Darcy’s Law, Equation 4.05 with and without the formation volume factor, B, (we want the flow rate in reservoir bbl/day not STB/day):
If we assume that the permeability, k, and the thickness, h, are uniform, then we have:
or,
or, after applying the chain rule:
Now, using the definition of compressibility for slightly compressible liquids:
Substituting Equation 4.51 into results Equation 4.50c in:
Equation 4.52 is the nonlinear diffusivity equation. We say that it is Nonlinear because the two density terms in the equation are functions of pressure. In this nonlinear form, we cannot solve the equation analytically (exactly). In order to obtain analytical solutions to this equation, we must first Linearize it. To do this, we apply the chain rule to the left-hand side of Equation 4.52:
or,
Note that the term, , is the first derivative squared and not the second derivative, . To complete the linearization process, we must assume the pressure gradient, , is small. If this is the case, then is very small, and we can remove it from Equation 4.53b:
or,
Which we can put into the compact format as:
or,
Where:
- 0.006328 is an equation constant (5.615 x 0.001127)
- is the radial coordinate in a radial-cylindrical coordinate system, ft
- is the pressure, psi
- is the porosity of the reservoir, fraction
- is the liquid viscosity, cp
- is the liquid compressibility, 1/psi
- is the reservoir permeability, md
- is time, days
- is the hydraulic diffusive , ft2/day
Equation 4.55 is the linear form of the diffusivity equation that describes the transient flow of a slightly compressible liquid through porous media. As we have already shown, solutions to this equation are useful in pressure transient analysis. The solutions to the diffusivity equation also have applications in the oil and gas production in:
- Rate Transient Analysis (analysis of time-dependent production rates)
- Type Curve Analysis (analysis of production rates using generalized, dimensionless plots)
- Unsteady-State Aquifer Performance (performance of aquifers in contact with hydrocarbon reservoirs)
The name Diffusivity Equation comes from the fact that this equation governs the diffusion process (with appropriate changes to the equation parameters and variables to make it relevant for diffusion). In addition, this equation also governs the process of heat conduction in solids, again, with appropriate changes to the equation parameters and variables.
4.5: Field Performance of Oil Reservoirs
To this point in the lesson, we have focused on the performance of individual wells. As reservoir engineers, we are also interested in the overall performance of the reservoir. It is important to note that we cannot simply sum the rates of the individual wells to determine the performance of the reservoir in its entirety. This is because Well Interference (interaction between wells) often occurs in the reservoir, which is not properly accounted for in our individual well analyses. This well interference occurs when the pressure disturbance caused by production from one well travels and comes into contact with the pressure disturbance caused by another well.
4.5: Field Performance of Oil Reservoirs section of this lesson will cover the following topics:
- 4.5.1: Field and Well Performance of Oil Reservoirs by Material Balance [31]
- 4.5.2: Field and Well Performance of Oil Reservoirs by Decline Curve Analysis [36]
Note: You can access specific subsections of the lesson by clicking on the links above or continue reading through the lesson using the link below.
4.5.1: Field and Well Performance of Oil Reservoirs by Material Balance
4.5.1: Field and Well Performance of Oil Reservoirs by Material Balance section of this lesson will cover the following topics:
- 4.5.1.1: Volumetric, Undersaturated Oil Reservoirs [32]
- 4.5.1.2: Non-Volumetric, Undersaturated Oil Reservoirs [35]
Note: You can access specific subsections of the lesson by clicking on the links above or continue reading through the lesson using the link below.
4.5.1.1: Volumetric, Undersaturated Oil Reservoirs
We were introduced to the concept of material balance earlier in this lesson when we discussed the derivation of the diffusivity equation. As we discussed in Lesson 2, an undersaturated oil reservoir is defined as a reservoir in which the initial pressure is greater that the bubble-point pressure of the crude oil. This results in a single, liquid hydrocarbon phase in the reservoir. As we discussed, there will be some water saturation in the reservoir also.
In this section, we will discuss the material balance method for Volumetric Reservoirs (reservoirs where the pore volume occupied by hydrocarbons remains constant with time – and pressure depletion). The Material Balance Method is applicable for both the reservoir in its entirety and to individual wells. From the volumetric method for estimating in-place fluids, we know that:
I have simplified this version of the equation (from Equation 4.04a) by assuming that the bulk volume in bbls, , is based on the net rock volume (that is, the net-to-gross ratio and the unit conversion constant, 5.615 ft3/bbl, have already been applied); the initial gas saturation is zero (because the reservoir is above the bubble-point pressure); and the water saturation is at its minimum value of .
In the Volumetric Method for STOOIP determination discussed earlier, all of the pressure dependent properties are evaluated at the initial reservoir pressure. Equation 4.56 is valid for any pressure conditions. If we evaluate Equation 4.56 twice, once at the initial conditions and once at some arbitrary, future condition (), then we would have:
and
Subtracting these two equations results:
Now, in this equation is the change in the oil-in-place (STB) in the reservoir from the initial condition to the future condition. Now, from material balance (mass is neither created nor destroyed), this change in mass is due to the expansion of the oil and must have been the mass of the oil produced from the wells during the time period, :
To make Equation 4.58b more convenient, we can substitute Equation 4.57a back into the equation:
or after multiplying both sides by the oil formation volume factor, , and rearranging:
Where:
- is the stock tank oil originally oil-in-place, STB
- is the oil-in-place at a future date, STB
- is the net rock volume, bbl
- is the porosity averaged over the reservoir, fraction
- is the irreducible water saturation averaged over the reservoir, fraction
- is the initial oil formation volume factor averaged over the reservoir, bbl/STB
- is the oil formation volume at a future time averaged over the reservoir, bbl/STB
- is the change in oil-in-place, STB
- is the oil production, STB
Equation 4.58d is the Material Balance Equation for volumetric reservoirs containing an undersaturated crude oil which remain above the bubble-point pressure. In this equation, the left-hand side represents the reservoir barrels removed from the reservoir through the production wells, while the right-hand side represents the expansion of oil in the reservoir. This equality is the general principle of material balance. We can use this equation in two ways:
- as a method to determine the STOOIP of the reservoir
- make future reservoir forecasts
4.5.1.1.1: Material Balance Method for Estimating the Stock Tank Oil Originally In-Place
In our earlier discussion on the estimation of Stock Tank Oil Originally In-Place, I mentioned that the two methods available for this task were the Volumetric Method and the Material Balance Method. We are now in a position to discuss the use of material balance for the estimation of the original oil-in-place in the reservoir. If we solve Equation 4.58d for STOOIP, , then we have:
Now in the field, if we accurately meter the oil production, , and actively measure average reservoir pressures (to evaluate ), then we can estimate and plot (on the y-axis) and on the x-axis (or, alternatively, time, t, on the x-axis). This results in a plot like that shown in Figure 4.08.

If all of the assumptions inherent in the development of Equation 4.59 are valid, then the data in Figure 4.08 should plot as a straight line with a zero slope and a y-intercept of (STOOIP), that is, the green curve in this figure. If these assumptions are not valid and there is more energy in the system other than the oil expansion, then the data will plot as a non-idealized curve, that is, the red curve.
The use of the material balance method to evaluate the original oil-in-place has several requirements associated with it. First, the Material Balance Method requires that production data are available. Therefore, it requires that the reservoir has been producing for some Historical Production Period (time period where the field has been on production). We must also have accurate estimates of the produced oil, , during this historical production period. This is typically a good assumption because we are selling the oil and must have accurate estimates for all of our sales obligations. In addition, it assumes that we have accurate estimates of the average reservoir pressure, , with time. This is part of a standard data acquisition program in the field and typically requires the involvement of reservoir engineers, production engineers, and geologists for good, representative estimates of average pressure. Finally, we must have accurate laboratory measurements of the formation volume factors, .
4.5.1.1.2: Material Balance Method for Making Future Reservoir Predictions
If we know the original oil-in-place from either the Volumetric Method or the Material Balance Method, then we can use Equation 4.58d to make future forecasts of reservoir performance with cumulative oil production, . We can do this by simply assuming average reservoir pressures, ; evaluating anticipated production at that pressure, , using Equation 4.58d; and estimating the stabilized oil production rate using either Equation 4.34 or Equation 4.40. Figure 4.09 shows a typical reservoir forecast in terms of .
In Figure 4.09, the historical production period is shown with the solid green data points and solid trendline, while the forecast is shown with the dashed green line. The noisy historical production data are a result of metering errors.
As I mentioned during our discussion on stabilized pressures, the use of in the drawdown calculation of the inflow performance is more consistent with material balance concept than the use of in the drawdown. This is because material balance is based on averaged reservoir properties. Therefore, for making predictions Equation 4.34 or Equation 4.40 should be used.

4.5.1.2: Non-Volumetric, Undersaturated Oil Reservoirs
In the development of Equation 4.58d, we assumed that the reservoir was volumetric (the pore-volume occupied by the oil was constant, and oil production was due to oil expansion only). If we remove this restriction and allow the pore-volume and rock to expand, then the volume of oil displaced to the wells (in bbl) becomes:
We have already seen that expansion of the original oil-in-place (in bbl) was described by Equation 4.58d:
The expansion of the water and rock can be determined by the definitions of compressibility. These definitions were given by Equation 3.21 and Equation 3.32. If we assume the initial pressure is the reference pressure, then:
Now, the expansion of water (in bbl) becomes:
Note that the use of this equation implies that the water volume is becoming larger (expanding) as the average pressure, decreases.
The change in pore-volume (in bbl) becomes:
Note that the use of this equation implies that the pore-volume is becoming smaller (contracting) as the average pressure, , decreases.
Both the increase in the water volume and the decrease in the pore-volume cause oil to be expelled from the reservoir, resulting in an increase in oil production (in bbl):
or,
Where:
- , , , and are the volume changes, bbl
- is the stock tank oil originally oil-in-place, STB
- is the initial oil formation volume factor averaged over the reservoir, bbl/STB
- is the oil formation volume at a future time averaged over the reservoir, bbl/STB
- is the net rock volume, bbl
- is the pore-volume, bbl
- is the pore-volume, bbl
- is the initial porosity averaged over the reservoir, fraction
- is the current porosity averaged over the reservoir, fraction
- is the irreducible water saturation averaged over the reservoir, fraction
- is the current water saturation averaged over the reservoir, fraction
- is the water compressibility, 1/psi
- is the rock, pore-volume compressibility, 1/psi
- is the current pressure averaged over the reservoir, psi
- is the current pressure averaged over the reservoir, psi
- is the oil production, STB
Equation 4.65b is the Material Balance Equation for Non-Volumetric, Undersaturated Reservoirs that remain above the bubble-point pressure. This equation will become more complicated as we add additional expansion terms. We can simplify the material balance equation using standard Society of Petroleum Engineering symbols as:
Where:
- is the sum of all Flow (production) from the reservoir, bbl
- is the stock tank oil originally oil-in-place, STB
- is the total Expansion of the system, bbl/STB
Again, we can use this equation for estimating the original oil-in-place and making future reservoir forecasts. To estimate the original oil-in-place, we divide Equation 4.66 by and plot (y-axis) versus (x-axis), (similar to how we generated Figure 4.08).
Equation 4.65b is valid for reservoirs with oil production caused by the expansion of the rock and fluids. It will now be instructive to go back to our discussion on the Drive Mechanisms for Oil Reservoirs. In that discussion, we listed all of the drive mechanisms associated with oil production and their approximate recovery factors (see Table 4.01). These drive mechanisms are:
- rock and fluid expansion
- solution gas drive
- gas cap drive
- gravity drainage
- natural aquifer drive (or water encroachment)
Without going into the details of the of each drive mechanism, Table 4.03 lists the expansion terms and production associated with each.
| Reservoir Drive Mechanisms in Terms of Standard Rock and Fluid Properties (from Lesson 3) | ||||
|---|---|---|---|---|
| Drive Mechanism | Expansion | Quantified | Production | Maximum Recoveries |
| Rock and Fluid Expansion | Oil Expansion | Up to 5 percent | ||
| Water Expansion (Interstitial Water) |
Up to 5 percent | |||
| Rock Expansion | Up to 5 percent | |||
| Solution Gas Drive | Solution Gas Expansion | 20 percent | ||
| Gas Cap Drive | Gas Cap Expansion | 30 percent | ||
| Gravity Drainage | Gravity Drainage | Not explicit in Material Balance Equation | 40 percent | |
| Natural Aquifer Drive | Water Encroachment | 45 percent | ||
| Production | ||||
| Drive Mechanism | Expansion | Quantified | Production | Maximum Recoveries |
| Production | Oil Production | |||
| Gas Production | ||||
| Water Production | ||||
Using the definitions shown in Table 4.03, we can rewrite Equation 4.66 as:
Where the entries in Equation 4.67 are listed in Table 4.04.
| Term | Description |
|---|---|
| Total volume of withdrawal (production) at reservoir conditions in bbl: and (SCF/STB) and (ft3/SCF) | |
| Cumulative oil Production in bbl | |
| Cumulative gas production in bbl | |
| Cumulative GOR (Gas-Oil Ratio) = Total gas produced over time divided by total oil produced over time. | |
| Cumulative water production in bbl | |
| Total expansion in the reservoir in bbl/STB: (bbl/STB) and (ft3/SCF). | |
| Total expansion of the oil and liberated gas dissolved in it. Expansion of the oil (above the bubble-point pressure) or shrinkage of the oil (below the bubble-point pressure due to liberation of gas) plus the expansion of the liberated gas | |
| is the ratio of gas cap volume, (SCF), to original oil volume, (bbl). A gas cap also implies that the initial pressure in the oil column must be equal to the bubble-point pressure. Note: is dimensionless. | |
| Expansion of the original of initial free gas (gas cap). | |
| Even though water has low compressibility, the volume of interstitial water in the system is normally large enough to be significant. The water will expand to fill the emptying pore-volume as the reservoir depletes. As the reservoir is produced, the pressure declines and the entire reservoir pore-volume is reduced due to compaction. The change in volume expels an equal volume of fluid (as production) and is additive in the expansion terms. | |
| If the reservoir is connected to an active aquifer, then once the pressure drop is communicated throughout the reservoir, the water will migrate into the reservoir resulting in a net water encroachment, in bbl. |
4.5.2: Field and Well Performance of Oil Reservoirs by Decline Curve Analysis
To this point in the lesson, everything that we have discussed is theoretical. That is, we developed these methods from first principles: Darcy’s Law, the definition of compressibility, basic rock and fluid properties, etc. Decline curve analysis is an Empirical Method (method based on observations) that is commonly used the oil and gas Industry. We will complete this lesson with a discussion on decline curves.
4.5.2: Field and Well Performance of Oil Reservoirs by Decline Curve Analysis section of this lesson will cover the following topics:
Note: You can access specific subsections of the lesson by clicking on the links above or continue reading through the lesson using the '>' link below.
4.5.2.1: Field and Well Performance with Arps Decline Curves
In a classic paper, J. J. Arps[1] took many observations from other investigators and concluded that the decline in the oil production rate, , over time from actual oil reservoirs could be described by the equations:
where the decline rate, , is a time dependent function:
Where:
- is the oil production rate, STB/day
- is the time, days (other units of time, such as months or years, can be used with an appropriate unit conversion constant)
- is the time dependent decline rate (time dependence defined by Equation 4.63), days-1
- is the initial decline rate (constant), days-1
- is a constant (typically used as a tuning parameter to match actual field data) and is in the range of , dimensionless
Decline curve analysis is essentially a curve fitting, or trend-line, analysis procedure where the form of the trend-line is developed from Arps[1] observations (Equation 4.68 and Equation 4.69). In this procedure, once the form of the trend-lines is established, we can use the parameters, , ,and to best match the data. We can develop these trend-lines or rate-time relationships if we integrate Equation 4.68 with respect to time. The resulting relationships have three forms depending on the value of the b-parameter.
[1] Arps, J. J.: “Analysis of Decline Curves,” SPE-945228-G, Trans. of the AIME (1945)
4.5.2.1.1: Exponential Decline (b=0)
If , then from Equation 4.69, , and we can integrate Equation 4.68 to obtain:
or,
Equation 4.70b is one of the rate-time relationships observed by Arps[1]. This equation is referred to as Exponential Decline because of the presence of the exponential term. We can also develop a rate cumulative production relationship by noting that:
Multiplying Equation 4.70b by and integrating results in:
or, after substituting Equation 4.70b into Equation 4.72a:
or, finally:
Equation 4.72 is the rate cumulative production relationship for exponential decline. The form of Equation 4.72b has two important applications. First, if we know the Abandonment Rate for the reservoir or well, , (rate at which the revenue from the oil sales would pay for the operating expenses of the reservoir or well), then we would have:
This would tell us the volume of oil that the reservoir or well would produce above the economic threshold. The second application of Equation 4.72b is if we would like to determine the production from the reservoir or well at an infinite time regardless of the economics. The volume of oil that can be recovered from a reservoir or well with no regard to the economics is called the Estimated Ultimate Recovery, or EUR, of the reservoir or well. We can determine the EUR by simply allowing the rate from reservoir or well to decline to 0 STB/day production rate (infinite time). That is:
The form of Equation 4.72c has one important application: to make future well forecasts. We can see that Equation 4.72c is a straight line in with a slope of (compare this straight-line relationship to the plot in Figure 4.09). Exponential decline is most often associated with the Rock and Fluid Expansion Drive Mechanism. In exponential decline, we have two parameters, and , with which to match the field data.
[1] Arps, J. J.: “Analysis of Decline Curves,” SPE-945228-G, Trans. of the AIME (1945)
4.5.2.1.2: Hyperbolic Decline (0<b<1)
If is in the range, , then the integration of Equation 4.68 and Equation 4.69 results in the rate-time relationship:
While a second integration with respect to time results in the rate-cumulative production relationship:
When the constant is in the range , we refer to the resulting production decline as Hyperbolic Decline. In hyperbolic decline, we have all three parameters, , , and , with which to match the field data.
4.5.2.1.3: Harmonic Decline (b=1)
If , then the integration of Equation 4.68 and Equation 4.69 results in the rate-time relationship:
While a second integration with respect to time results in the rate-cumulative production relationship:
When , we refer to the resulting production decline as Harmonic Decline. In harmonic decline, we have two parameters, and , with which to match the field data. Table 4.05 summarizes the results of Arps[1] Decline Curve Analyses.
| Relationship | Exponential Decline |
Hyperbolic Decline |
Harmonic Decline |
|---|---|---|---|
| Range of b-parameter | |||
| Rate-Time Relationship | |||
| Cumulative Production-Time Relationship | |||
| Rate-Cumulative Production Relationships | or |
or |
or |
| Maximum Economic Recovery | |||
| Estimated Ultimate Recovery, EUR |
Table 4.05 indicates that the EUR of a reservoir or well undergoing harmonic decline will be infinity. For this reason, a value of is considered to be an upper limit of this parameter. It is rarely used in any real analyses and is considered the theoretical maximum value of the parameter .
Using the relationships in Table 4.05, we can constrain (bracket) our production forecast from the Material Balance Method. This is shown in Figure 4.10. This figure illustrates why harmonic decline leads to an infinite EUR – the production can never achieve a zero rate and the area under the curve becomes infinite.
Finally, the decline curves allow us to convert the forecasts to forecasts.

Since decline curve analysis is a curve fitting, trend-line analysis technique, one important assumption in the use of decline curves is that whatever processes that occurred in the past that helped to establish the trend of the data must continue to occur into the future. This includes naturally occurring processes, such as, no changes in the reservoir drive mechanism, and operational changes, such as, no change to the specified flowing pressures of the wells, .
[1] Arps, J. J.: “Analysis of Decline Curves,” SPE-945228-G, Trans. of the AIME (1945)
4.6: Key Learnings
- Three of the key tasks performed by reservoir engineers are the estimation of the Stock Tank Oil Originally in-Place, STOOIP, in an oil reservoir or drainage volume, estimation of the stabilized production rate from a well, forecast future performance of an oil reservoir or well.
- Two common methods for calculating the STOOIP in an oil accumulation are:
- The Volumetric Method
- The Material Balance Method
- Drive mechanisms are the physical phenomena that keep reservoir pressures high and cause fluids to move to lower pressure areas in the reservoir. There are five drive mechanisms in an oil reservoir:
- Rock and fluid expansion
- Solution gas drive
- Gas cap drive
- Gravity drainage
- Natural aquifer drive (or water encroachment)
- The major flow regimes experienced by vertical production wells occur in sequence due to the pressure disturbance caused by production propagating radially outward from the well. These flow regimes are:
- Well dominated flow
- Transient flow
- Late transient flow
- Boundary dominated flow
- The stabilized production rates from a production well occur during the boundary dominate flow regime. These stabilized production rates are governed by the inflow performance relationships.
- Well damage or stimulation can occur in all production wells. Well damage/stimulation is quantified by the Skin Factor. A positive (+) skin factor results from well damage, while a negative (-) skin factor results from well stimulation.
- Two common methods for making future reservoir or well forecasts are:
- The Material Balance Method
- Decline curve analysis
- Exponential decline
- Hyperbolic decline
- Harmonic decline
4.7: Summary and Final Tasks
Summary
In this lesson, we discussed three very important tasks performed by reservoir engineers:
- estimation of the Stock Tank Oil Originally In-Place or STOOIP
- estimation of the stabilized production rate from a vertical oil well
- forecasting the future performance of oil reservoir and wells
We saw that there were two methods commonly used in the oil and gas industry estimating the STOOIP:
- the Volumetric Method
- the Material Balance Method
We discussed that of these two methods, the material balance method is typically assumed to be more accurate as it is based on dynamic data.
We also discussed the five Drive Mechanisms associated with oil reservoirs:
- Rock and fluid expansion
- Solution gas drive
- Gas cap drive
- Gravity drainage
- Natural aquifer drive (or water encroachment)
Later in the lesson, we saw how these drive mechanisms could be quantified and put into the material balance equation
We also discussed the stabilized production rates from vertical oil production wells. We saw that there were several flow regimes possible in a hydrocarbon reservoir that occurred at different stages in a well’s productive life. In Figure 4.06, we saw that these flow regimes occurred sequentially as the pressure disturbance caused by production propagates outward from the well. These flow regimes are:
- Well dominated flow
- Wellbore storage
- Damage/Stimulation
- Transient flow
- Late transient flow
- Boundary dominated flow
- Steady-state
- Pseudo steady-state
The well dominated flow regime is controlled by well properties and well damage/stimulation, not reservoir properties. The transient flow regime is governed by the diffusivity equation and is characterized by time-dependent rates and/or pressures. The onset of the late transient period occurs when the pressure disturbance from the production well reaches the first boundary of the drainage volume. The end of the late transient period occurs when the pressure disturbance reaches the last boundary of the drainage volume. The boundary dominated flow regime is the last regime experienced by the well. It is during this period that stabilized production occurs. Stabilized production is described by one of the Inflow Performance Relationships shown in Table 4.02.
For forecasting future reservoir or well performance, we discussed two methods:
- The Material Balance Approach
- Decline Curve Analysis
- Exponential decline
- Hyperbolic decline
- Harmonic decline
The Material Balance Method is an analytical (theoretically based) approach based on measured rock and fluid properties. It accounts for all drive mechanisms encountered in the field. Gravity drainage is considered implicitly in the choice of the datum depth used to evaluate the reservoir pressures. Decline curve analysis is an empirical (observation based) approach that uses trends in the observed data and analysis of these trends using simple mathematic expressions. Decline curve analysis is categorized based on the value of the b-parameter: exponential , hyperbolic , and harmonic .
Harmonic decline results in unrealistic EURs and is typically used as the theoretical limit for the b-parameter.
Final Tasks
Complete all of the Lesson 4 tasks!
You have reached the end of Lesson 4! Double-check the to-do list on the Lesson 4 Overview page [41] to make sure you have completed all of the activities listed there before you begin Lesson 5.
Lesson 5: Reservoir Engineering for Gas Reservoirs
5.0: Lesson Overview
In this lesson, we will discuss Reservoir Engineering for natural gas reservoirs. The tasks performed by reservoir engineers working on gas fields are much the same as those performed for oilfields. These tasks include estimating the original-gas-in-place, or OGIP, analyzing current production rate and pressure trends from the wells and the reservoir, forecasting future performance from these trends, and determining the economic recovery and the Estimated Ultimate Recovery (EUR) of a well, reservoir, or field.
The main difference between natural gas as a produced phase and oil as a produced phase is the highly compressible nature of gas. In many of the methods we discussed for oil reservoirs, we assumed that the oil phase compressibility obeyed the definition of compressibility for a slightly compressible liquid, Equation 3.47:
Natural gas is a Real Gas, and as such, it will obey the Real Gas Law, Equation 3.27:
The fact that natural gas is a real gas and obeys the Real Gas Law has many significant ramifications to the reservoir engineering tasks that we have discussed. In this lesson, we will use the Real Gas Law to develop our equations for the stabilized inflow performance relationships, the transient diffusivity equation, material balance equation, and decline curve analysis.
Learning Objectives
By the end of this lesson, you should be able to:
- discuss the difference between compressible fluids (gases) and slightly compressible fluids (crude oils);
- discuss two methods of calculating the Original-Gas-in-Place, OGIP, in a gas accumulation;
- calculate the OGIP of a natural gas reservoir using the Volumetric Method and Material Balance Method given appropriate data;
- list and describe the four drive mechanisms associated with gas production;
- calculate the stabilized production rates from a gas production well given the current flow regime and given appropriate data;
- list the three formulations used in the stabilized production rates from a gas production well and the pressure ranges where these formulations are appropriate;
- forecast future production from a natural gas reservoir or production well using the Material Balance Method and Decline Curve Analysis given appropriate data; and
- estimate the economically recoverable gas and Estimated Ultimate Recovery (EUR) from a natural gas reservoir
Lesson 5 Checklist
| To Read | Read the Lesson 5 online material | Click the Introduction link below to continue reading the lesson 5 material |
|---|---|---|
| To Do | Lesson 5 Problem Set | Submit your solutions to the Lesson 5 Problem Set assignment in Canvas |
Please refer to the Calendar in Canvas for specific time frames and due dates.
Questions?
If you have questions, please feel free to post them to the Course Q&A Discussion Board in Canvas. While you are there, feel free to post your own responses if you, too, are able to help a classmate.
5.1: Introduction
In Lesson 3, we discussed basic Rock, Fluid, and Rock-Fluid Interaction properties; while in Lesson 4, we applied these properties to oil reservoirs. In this lesson, we will discuss how these properties are used by reservoir engineers working on gas reservoirs.
The tasks for reservoir engineers working on gas wells or gas fields are much the same as the tasks involved for oilfields: the estimation of the original gas-in-place, OGIP, and the estimation of the rates and volumes of fluids produced from the production wells and from the field. For in-place fluid calculations, the Volumetric Method and the Material Balance Method are just as applicable for gas reservoirs as they are for oil reservoirs. We will see, however, that there are differences in the forms of the equations due to the compressible nature of gas. In addition, we will see that the stabilized Inflow Performance Relationships, IPR, (boundary dominated well production rates from Darcy’s Law) and the time dependent diffusivity equation are also impacted by the compressible nature of the gas.
5.2: Estimation of Original Gas In-Place, OGIP, Using the Volumetric Method
The Volumetric Method for OGIP is essentially the same for gas reservoirs. The method uses static geologic data to determine the volume of the pore space of the reservoir. Once the volume of the pore space is estimated, then the gas formation volume factor, can be used to estimate the OGIP.
By simply using the definition of reservoir volumes, the original-gas-in-place of the reservoir be determined by:
or, equivalently (after applying the Saturation Constant):
Where:
- is the original-gas-in-place of the reservoir, SCF
- is the gross rock volume, ft3
- is the net-to-gross thickness ratio, fraction
- is the average net reservoir thickness, ft
- is the average gross reservoir thickness, ft
- is the average initial gas saturation, fraction
- is the average initial water saturation, fraction
- is the average reservoir porosity, fraction
- is the average formation volume factor of the gas at initial conditions (pri and Tr), ft3/SCF
As with the oil volumetric equation (Equation 4.02), Equation 5.01 is evaluated at initial pressure and saturation conditions because the original in-place volume is the desired result. Also, as with the volumetric oil equation, the net-to-gross ratio in the volumetric gas equation is simply the thickness fraction that converts the total reservoir thickness to the thickness that contributes to hydrocarbon storage and flow in the reservoir. We use thickness to apply the net-to-gross ratio because rock formations are formed as layers during deposition, and we assume that layers of poor-quality rock may be deposited and intermixed with layers of good quality reservoir rock. We can further define the gross rock volume as:
Where:
- is the gross rock volume, ft3
- is a unit conversion constant, ft2/acre
- is the mapped area of the reservoir, acres
- is the average gross reservoir thickness, ft
As with oil reservoirs, the volumetric method for estimating the in-place volumes is also considered to be less accurate than the material balance method. The reason again being the use of all of the averages in Equation 5.01. This can also be improved by the use of the iso-contour technique describe in Lesson 4.
5.3: Drive Mechanisms in Gas Reservoirs
In Lesson 4, we discussed the drive mechanisms associated with oil reservoirs. For gas reservoirs, there are three drive mechanisms that are associated with conventional gas reservoirs and a fourth drive mechanism associated with unconventional gas reservoirs. These are:
- gas expansion (most significant drive mechanism in conventional gas reservoirs);
- gas desorption (may only be present in certain unconventional gas reservoirs);
- rock and fluid expansion (expansion of the reservoir rock and interstitial water – typically only significant in over-pressured gas reservoirs); and
- natural aquifer drive (or water encroachment).
In this list, I make a distinction between Conventional and Unconventional Gas Reservoirs. Conventional gas reservoirs are reservoirs with sufficiently high permeability to allow for production using conventual well technologies. Unconventional reservoirs are reservoirs with low permeabilities that require special production technologies that allow for economic recoveries of gas. Typically, the threshold to define an unconventional gas reservoir is a reservoir with a permeability less than 0.1 md.
Gas expansion is the primary drive mechanism in most conventional gas reservoirs. Again, the analogy of a gas-filled balloon a very appropriate analogy. If a balloon is filled with high pressure gas and the end is opened to the low pressure atmosphere, then gas will expand and exit the balloon. This mechanism is very efficient and commonly results in recoveries as high as 85 percent of the original-gas-in-place.
A drive mechanism that is associated with certain unconventional gas reservoirs is gas desorption. As we have already discussed, unconventional gas reservoirs are reservoirs with permeabilities less than 0.1 md. These unconventional reservoirs include:
- tight oil and gas sandstones or carbonates;
- shale gas and shale oil reservoirs; and
- coal seam methane reservoirs.
The last two of these unconventional gas reservoir types, shale gas reservoirs and coal seam methane reservoirs, have a high content of organic material in the reservoir rock. This organic rich rock material has the ability to Adsorb gas onto its surface (gas stored by adhesion onto the surface). As pressure is depleted, this adsorbed gas is released to the pore-volume of the reservoir by the Desorption Process. This desorption of gas may dominate production from the unconventional gas reservoirs in which it occurs.
Rock and fluid expansion in gas reservoirs is identical to that in oil reservoirs. It occurs due to the slightly compressible nature of the Interstitial (or Connate) Water and the reservoir rock. This expansion adds energy to the reservoir and acts to keep the reservoir pressure higher than it would be otherwise. This expansion mechanism is always dominated by gas expansion and may only be significant in cases of over-pressured reservoirs.
The final drive mechanism associated with conventional gas reservoirs is aquifer drive, or water encroachment. As with oil reservoirs, this drive mechanism occurs when the reservoir is in communication with a water-bearing aquifer. As the reservoir pressure declines, the rock and water in the aquifer expand, and water is expelled from the aquifer and into the reservoir. This encroachment of water into the reservoir provides pressure support.
These last two drive mechanisms may be slightly deceptive as to whether they aid in gas production or not. Both of these methods tend to keep reservoir pressures high; however, the principle drive mechanisms, gas expansion, and gas desorption, rely on pressure depletion. In addition, water encroachment may also result in trapped gas behind the invading water front.
5.4: Performance of Gas Wells
5.4: Performance Gass Wells section of this lesson will cover the following topics:
- 5.4.1: Stabilized Inflow Performance of Gas Wells [42]
- 5.4.1.1: Stabilized Flow of Gas to a Vertical Production Well in Terms of Pressure [43]
- 5.4.1.2: Stabilized Flow of Gas to a Vertical Production Well in Terms of Pressure-Squared [44]
- 5.4.1.3: Stabilized Flow of Gas to a Vertical Production Well in Terms of the Real Gas Pseudo-Pressure, m(p) [45]
- 5.4.1.4: The Rawlins and Schellhardt Backpressure or Deliverability Equation [46]
- 5.4.2: Transient Performance of Gas Wells [47]
- 5.4.2.1: Derivation of the Diffusivity Equation in Radial-Cylindrical Coordinates for Compressible Gas Flow [48]
- 5.4.2.2: The Diffusivity Equation for a Gas in Radial-Cylindrical Coordinates in Terms of Pressure [49]
- 5.4.2.3: The Diffusivity Equation for a Gas in Radial-Cylindrical Coordinates in Terms of Pressure-Squared [50]
- 5.4.2.4: The Diffusivity Equation for a Gas in Radial-Cylindrical Coordinates in Terms of Real Gas Pseodo-Pressure, m(p) [51]
5.4.1: Stabilized Inflow Performance of Gas Wells
We have already discussed, the stabilized production of gas is similar to the flow of oil; however, due to the compressible nature of gas, we must consider the pressure dependencies of the gas properties more rigorously than we did for oil. I will again start with the steady-state inflow performance relationship.
For steady-state analysis, we need to make the following assumptions:
- Flow is steady-state and Darcy’s Law applies and all of the assumptions inherent Darcy’s Law are valid in the system
- The drainage volume is radial-cylindrical (see Figure 4.01)
- The drainage volume is bounded in the interior with a cylindrical well (radius equal to ) and kept at flowing well pressure of
- The drainage volume is bounded on the exterior with a cylindrical boundary (radius equal to ) which has an external pressure of
- The drainage volume is bounded on the top and bottom (constant height) no-flow boundaries
- Within the drainage volume, the rock properties are homogeneous (uniform with location)
- Within the drainage volume, the rock properties are isotropic (uniform in all directions)
- Flow is horizontal
With these assumptions, we can use the single-phase version of Darcy’s Law:
In Equation 5.03, we are using the effective permeability to gas in the presence of a water phase to allow for an irreducible, immobile water phase in the reservoir. Now, for radial flow, we have:
Substituting into Darcy’s Law, we have:
Separating variables and integrating results in:
Now, using the assumption of a homogeneous permeability, we have:
To this point, the derivation of the stabilized inflow performance relationship for gas is identical to the derivation for oil. In the derivation of the inflow performance relationship for oil, we assumed that were constant, and we removed them from the integral. As stated earlier, the properties, and , are pressure dependent properties due to the compressible nature of gas and may need to be treated differently from the treatment of the oil properties. These differences manifest themselves in how we treat the integral in Equation 5.08.
There are three methods used in the industry to evaluate the integral in Equation 5.08. These methods lead to three different formulations for the inflow performance relationship for gas. These are:
- Stabilized Production of Gas in Terms of Pressure
- Stabilized Production of Gas in Terms of Pressure-Squared
- Stabilized Production of Gas in Terms of Pseudo-Pressure
In addition to these three analytical inflow performance relationships, we will discuss one common empirical inflow performance relationship, the Rawlins and Schellhardt Backpressure or Deliverability Equation[1].
[1] Rawlins, E.L. and Schellhardt, M.A. 1935. Backpressure Data on Natural Gas Wells and Their Application to Production Practices, 7. Monograph Series, U.S. Bureau of Mines.
5.4.1.1: Stabilized Flow of Gas to a Vertical Production Well in Terms of Pressure
To develop the inflow performance relationships for gas, we will need to use the definition of the gas formation volume factor, , Equation 3.68:
or,
Since Equation 5.08 is written in terms of bbl/day, we need use the form of in bbl/SCF. Substituting Equation 5.09 into Equation 5.08 results in:
Now, if we assume that the term, , is constant with pressure, then we can remove it from the integral (in essence, this is what we did for the oil equation). While at first glance, this may seem like a bad assumption because we are removing p and two pressure dependent functions, and , from an integration with respect to pressure; within certain pressure ranges it is not a bad assumption. This is because we are not interested in how the individual components in the group, , behave with respect to pressure but are concerned with how the group behaves in its entirety. I will discuss this in more detail later in this lesson. If we remove this group from the integral in Equation 5.10, then we obtain:
Performing the two integrations in Equation 5.11:
or,
Rearranging Equation 5.13 results in:
or,
Now, if we use the normal U.S. definitions of Standard Pressure and Standard Temperature , then we have:
Equation 5.14c is the steady-state inflow performance relationship for single-phase gas production. All that remains is to discuss how to evaluate the term, . Typically, we do this by evaluating the average pressure as the arithmetic mean pressure:
and use that average pressure to evaluate and . Because all of the pressure terms in this equation are written directly as , we refer to this formulation as the Inflow Performance Relationship for Gas in Terms of Pressure. As with the oil inflow performance relationship, we can add a skin factor to account for damage or stimulation and write similar equations in terms of (rather than ) for the pseudo steady-state flow regime.
5.4.1.2: Stabilized Flow of Gas to a Vertical Production Well in Terms of Pressure-Squared
To develop the inflow performance relationship in terms of pressure, we assumed that the group, , was relatively constant in the pressure range of interest, and we removed the entire group from the pressure integral in Equation 5.10. In the pressure-squared formulation, we assume that the product is relatively constant with pressure and remove it from Equation 5.10, leaving:
Again, we will see that the product can be safely assumed to be relatively constant over a particular pressure range. Performing both integrations in Equation 5.16 results in:
Rearranging Equation 5.17 results in:
or,
or, after substituting the normal U.S. definitions of and :
In this equation, we evaluate and at the arithmetic mean average pressure, Equation 5.15. Again, we can add a skin factor to account for well damage or stimulation and write similar equations in terms of average pressure for the pseudo-steady state flow regime. Equation 5.18c is the Inflow Performance Relationship for Gas in Terms of Pressure-Squared.
5.4.1.3: Stabilized Flow of Gas to a Vertical Production Well in Terms of the Real Gas Pseudo-Pressure, m(p)
In the two previous developments of the stabilized inflow performance relationship for gas (in terms of pressure and the pressure-squared), we made simplifying assumptions on the pressure dependency of the group, . I stated that within certain pressure ranges these assumptions were valid. However, there may be cases where these assumptions are not valid over the entire pressure range of interest. In these cases, we need to develop a general equation that is valid for all pressures. We can achieve this with the Real Gas Pseudo-Pressure Formulation. We define the real gas pseudo-pressure, , as:
The terminology, , implies that the real gas pseudo-pressure is a function of pressure. The units of are . We can see from Equation 5.19 that:
or,
The relationships expressed in Equation 5.20 are illustrated in Figure 5.01. In this figure, , is plotted on the y-axis and is plotted on the x-axis. The blue area under the curve represents while the total area (blue plus green areas) under the curve represents . These are two of the integrals in Equation 5.20. The green area under the curve then represents .

Substituting Equation 5.20b into Equation 5.10 results in:
Performing the integration on the left-hand side of Equation 5.21 results in:
Rearranging Equation 5.22 results in:
or,
or, after substituting the normal U.S. definitions of and :
The only thing remaining for the pseudo-pressure formulation is the construction of the function. To do this, we perform numerical integration on the function. There are many ways to perform numerical integration; however, one of the most common methods is to approximate the area under the curve with a series of rectangles and to sum the areas of these rectangles. This is illustrated in Figure 5.02.

Using this approach, we can approximate the integral (area under the curve) with:
The Real Gas Pseudo-Pressure Formulation is the most rigorous and general formulation for the inflow performance relationship for gas and is valid over all pressure ranges. Even in pressure ranges where another formulation may be valid, the real gas pseudo-pressure formulation is more rigorous.
As I just mentioned, there are pressure ranges where the Pressure Formulation and the Pressure-Squared Formulation are valid. If we were to plot the group (on the y-axis) versus on the x-axis, then we would develop the plot shown in Figure 5.03. This plot illustrates that the group is approximately constant for p > 3,000 psi and that the Pressure Formulation is valid when all pressures in the pressure range of interest are greater than 3,000 psi.

We can also plot (on the y-axis) versus on the x-axis to develop the plot shown in Figure 5.04. This plot illustrates that the product is approximately constant for p < 2,000 and that the Pressure-Squared Formulation is valid when all pressures are less than 2,000 psi.

5.4.1.4: The Rawlins and Schellhardt Backpressure or Deliverability Equation
One final relationship that is often used in the oil and gas industry is the empirical Rawlins and Schellhardt Backpressure or Deliverability Equation[1]. This equation has the form:
As with all observation-based empirical relationships, to use this equation it must be tuned with appropriate data to determine the values of the tuning parameters, and . To do this, the gas well must be produced at several flowing pressures, , and the resulting stabilized rates measured. Once these tests (Deliverability Tests) are performed, the equation parameters, and , are used to fit the equation to the test results. Table 5.01 a-g summarizes all of the Stabilized Inflow Performance Relationships for gas wells discussed to this point.
| In Terms of Pressure including Damage or Stimulation: All pressures greater than 3,000 psi |
||
|---|---|---|
| Steady-State Flow Regime | Pseudo Steady-State Flow Regime | |
| Drawdown | ||
| Productivity Index |
||
| IPR | ||
| In terms of Pressure including Damage or Stimulation: All pressures greater than 3,000 psi |
||
|---|---|---|
| Steady-State Flow Regime | Pseudo Steady-State Flow Regime | |
| Drawdown | ||
| Productivity Index |
||
| IPR | ||
| In terms of Pressure-Squared including Damage or Stimulation: All pressures less than 2,000 psi |
||
|---|---|---|
| Steady-State Flow Regime | Pseudo Steady-State Flow Regime | |
| Drawdown | ||
| Productivity Index |
||
| IPR | ||
| In terms of Pressure-Squared including Damage or Stimulation: All pressures less than 2,000 psi |
||
|---|---|---|
| Steady-State Flow Regime | Pseudo Steady-State Flow Regime | |
| Drawdown | ||
| Productivity Index |
||
| IPR | ||
| In terms of the Real Gas Pseudo-Pressure including Damage or Stimulation: Valid over the entire pressure range |
||
|---|---|---|
| Steady-State Flow Regime | Pseudo Steady-State Flow Regime | |
| Drawdown | ||
| Productivity Index |
||
| IPR | ||
| In terms of the Real Gas Pseudo-Pressure including Damage or Stimulation: Valid over the entire pressure range |
||
|---|---|---|
| Steady-State Flow Regime | Pseudo Steady-State Flow Regime | |
| Drawdown | ||
| Productivity Index |
||
| IPR | ||
| The Rawlins and Schellhardt Backpressure or Deliverability Equation[1] | ||
|---|---|---|
| Steady-State Flow Regime | Pseudo Steady-State Flow Regime | |
| IPR | ||
The following parameters are used in Table 5.01 or in the development of these equations:
- reservoir pressure at the external boundary of the drainage volume, psi
- flowing well pressure, psi
- average reservoir pressure within the drainage volume, psi
- the real gas pseudo-pressure, psi2/cp
- external radius of the drainage volume, ft
- radius of the well, ft
- pressure at standard conditions (14.7 psi in the U.S.A), psi
- temperature at standard conditions (520°R in the U.S.A), °R
- temperature of the reservoir, °R
- effective permeability to gas in the presence of an immobile water phase, md
- thickness of the reservoir, ft
- gas viscosity, cp
- gas super-compressibility factor, dimensionless
- skin factor, dimensionless
- is the oil production rate during the stabilized production period, SCF/day
- factor in Rawlins and Schellhardt Backpressure or Deliverability Equation[1], SCF/(day-psi(2xn))
- exponent in Rawlins and Schellhardt Backpressure or Deliverability Equation[1], dimensionless
- is the oil phase formation volume factor, bbl/SCF
5.4.2: Transient Performance of Gas Wells
In our earlier discussions on the performance of oil wells, we discussed transient (time dependent) flow and the flow regimes encountered during transient flow. These flow regimes also occur in gas wells and are:
- Well dominated flow
- Wellbore storage
- Damage/Stimulation
- Transient flow
- Late transient flow
- Boundary dominated flow
- Steady-state
- Pseudo steady-state
5.4.2.1: Derivation of the Diffusivity Equation in Radial-Cylindrical Coordinates for Compressible Gas Flow
As with the flow of oil, we begin the derivation of diffusivity equation for compressible gas flow with a mass balance on a thin ring or Representative Elemental Volume, REV, in the reservoir as shown in Figure 5.05. This mass balance results in:
We can elaborate on the definitions of terms in Equation 5.26 as:
and,
Where:
- is the gas density, lb/ft3
- is the gas rate, ft3/day
- is the radial coordinate in a radial-cylindrical coordinate system, ft
- is the radius of the representative elemental volume, REV, ft
- is time, days
- is the porosity of the reservoir, fraction
- is the bulk volume of the representative elemental volume, REV, ft3
- is the reservoir thickness, ft

Substituting Equation 5.27 through Equation 5.29 into Equation 5.26 results in:
or,
Dividing by the term results in:
Now, substituting Darcy’s Law, Equation 5.06 with and without the formation volume factor, , (we want the flow rate in reservoir ft3/day not SCF/day). The unit conversion factor of 5.615 ft3/bbl converts Darcy’s Law from bbl/day to ft3/day:
If we assume that the permeability, , and the thickness, , are uniform, then we have:
or,
To this point, the derivation for the compressible gas equation is identical to the derivation for a slightly compressible liquid equation. This derivation will begin to deviate now. Applying the definition of density for a real gas (Equation 3.71):
Equation 5.34 is a direct result of the Real Gas Law. Substituting into Equation 5.33b results in:
or,
or,
Now, we saw in Lesson 3 that for a real gas, the definition of compressibility is (Equation 3.70b):
or,
Substituting into Equation 5.35c results in:
Equation 5.37 is the nonlinear diffusivity equation describing the transient behavior of compressible (real) gases. We say that it is Nonlinear because of the functions of pressure appearing in the equation. In this nonlinear form, we cannot solve the equation analytically (exactly). In order to obtain analytical solutions to this equation, we must first Linearize it. We do this in the same manner as we linearized the stabilized flow equations: by use of the Pressure, the Pressure-Squared, and the Pseudo-Pressure Formulations.
5.4.2.2: The Diffusivity Equation for a Gas in Radial-Cylindrical Coordinates in Terms of Pressure
As we have already seen, in the pressure range of , the group can be considered to be approximately constant. With this simplification, we can remove the group from the spatial derivative on the left-hand side of Equation 5.37 to obtain:
This is the diffusivity equation for real gases in terms pressure, p. While this may at first glance appear to be linearized, it is not. Both the gas compressibility term, , and the gas viscosity term, , are pressure dependent. When using the pressure formulation, we typically evaluate these terms at either the initial pressure condition, , or the average condition, . (Note: other more rigorous methods are available for the evaluation of the product; however, they are beyond the scope of this course.)
5.4.2.3: The Diffusivity Equation for a Gas in Radial-Cylindrical Coordinates in Terms of Pressure-Squared
In the pressure-squared formulation, we assume that the product is constant. We have already seen that this approximation is valid for . With this simplification, Equation 5.37 becomes:
Now, we can use the identity:
or,
Substituting Equation 5.40b into Equation 5.39 results in:
This is the diffusivity equation for real gases in terms pressure-squared, . Again, the product represents a non-linear term which we evaluate at either the initial pressure, , or the average pressure, .
5.4.2.4: The Diffusivity Equation for a Gas in Radial-Cylindrical Coordinates in Terms of Real Gas Pseudo-Pressure, m(p)
Finally, we will investigate the use of the real gas pseudo-pressure in the diffusivity equation. For this, we differentiate the definition of the pseudo-pressure integral, Equation 5.19, using the fundamental theorem of calculus:
or,
Substituting Equation 5.42b into Equation 5.39 results in:
Again, we evaluate the product at either the initial pressure, , or the average pressure, . In this development, we have:
- is an equation constant (5.615 x 0.001127)
- is the radial coordinate in a radial-cylindrical coordinate system, ft
- is the pressure, psi
- is the real gas pseudo-pressure, psi2/cp
- is the porosity of the reservoir, fraction
- is the gas compressibility, 1/psi
- is the gas viscosity, cp
- is the effective permeability to gas, md
- is time, days
5.5: Field Performance of Gas Reservoirs
5.5: Field Performance of Gas Reservoirs section of this lesson will cover the following topics:
5.5.1: Field and Well Performance of Gas Reservoirs by Material Balance
Volumetric Gas Reservoirs
We were introduced to the concept of material balance in Lesson 4 when we discussed oil reservoirs. In this section, we will discuss the material balance method for Volumetric Gas Reservoirs (reservoirs where the pore-volume occupied by the gas remains constant with time and pressure depletion). We can approach the development of the material balance method from the perspective of the Volumetric Method, as we did in Lesson 4 for oil reservoirs, or from the perspective of the Real Gas Law. I will discuss both of these perspectives in this lesson.
From the perspective of the Volumetric Method for estimating in-place fluids, from Equation 5.01, we know that the original gas-in-place:
As I did for oil reservoirs, I simplified this version of the equation (from Equation 5.01) by assuming that the bulk volume , is in bbls and is based on the net rock volume (that is, the net-to-gross ratio and the unit conversion constant, 5.615 ft3/bbl, have already been applied). I also assumed that the water saturation is at its minimum value of .
Equation 5.44 is valid for any pressure conditions. In the Volumetric Method for OGIP estimation discussed earlier, all of the pressure dependent properties are evaluated at the initial reservoir pressure. If we evaluate Equation 5.44 twice, once at the initial conditions and once at some arbitrary, future condition (), then we would have:
and
Where and are in bbl/SCF (Equation 5.09b). Subtracting Equation 5.45b from Equation 4.45a results in:
in this equation is the change in the gas-in-place (SCF) in the reservoir from the initial condition to the future condition. Now, from material balance (mass is neither created nor destroyed), this change in mass is due to the expansion of the gas and must be equal to the mass of the cumulative gas produced from the wells during the time period, :
To make Equation 5.47 more convenient, we can substitute Equation 5.45a back into the equation:
or after multiplying both sides by the gas formation volume factor, , and rearranging:
Where:
- is the original-gas-in-place, OGIP, SCF
- is the current-gas-in-place, CGIP, at a future date, SCF
- is the net rock volume, bbl
- is the porosity averaged over the reservoir, fraction
- is the irreducible water saturation averaged over the reservoir, fraction
- is the initial gas formation volume factor averaged over the reservoir, bbl/SCF
- is the gas formation volume at a future time averaged over the reservoir, bbl/SCF
- is the change in gas-in-place, SCF
- is the gas production, SCF
This is the derivation of the Material Balance Equation for volumetric reservoirs containing a natural gas. In this equation, the left-hand side represents the reservoir barrels of natural gas removed from the reservoir through the production wells, while the right-hand side represents the expansion of natural gas in the reservoir. From the perspective of the Volumetric Equation (Equation 5.01), the Material Balance method states that the standard cubic feet of gas produced through the wells must equal the change in standard cubic feet in the pore-volume of the reservoir.
As I mentioned earlier, we can also look at the material balance method from the perspective of the Real Gas Law:
We start with a lb-mol balance in the reservoir where the lb-mols produced from the reservoir, , must equal the lb-mols initially in the reservoir, minus the lb-mols currently in the reservoir, ,:
Substituting the appropriate conditions on these quantities (standard conditions for , initial reservoir conditions for , and current reservoir conditions for ), we have:
In this equation, I used the definition of a Volumetric Reservoir (time invariant pore-volume) to remove the volume occupied by the gas from the parenthesis on the right-hand side of the equation. The unit conversion constant of 5.615 ft3/bbl was required because the units of are in barrels. Dividing by results in:
Factoring from the parenthesis results in:
Finally, noting that is the reciprocal of the initial gas phase formation volume factor, , and that is the original-gas-in-place, :
or,
Note that we could have easily substituted the definitions of the gas phase formation volume factors into Equation 5.52 to obtain Equation 5.48b. Also note that Equation 5.53c is the equation of a straight line with on the y-axis and on the x-axis. This is illustrated in Figure 5.06.

As with material balance for oil reservoirs, this equation and its plot can be used to make an estimate of the OGIP or to make future reservoir forecasts. We can estimate a future forecast of the volume produced, , at any reservoir pressure, , by simply dividing the pressure of interest by its corresponding Z-factor and looking up the cumulative gas produced, , at that value from the . For estimating the OGIP, we can see from Equation 5.53c, that the x-intercept () occurs when . Therefore, we can look at the x-intercept of the to estimate the OGIP, , directly.
In addition, we can use the as a diagnostic plot to help us identify the type of reservoir we are working with. Figure 5.07 shows common reservoir types on a .
Getting back to Equation 5.48b, we can also use it to estimate the original-gas-in-place and to make future forecasts. This is done by redefining terms in Equation 5.48b.
Where:
- is the sum of all Flow (production) from the reservoir, bbl
- is the original-gas-in-place, SCF
- is the total Expansion of the system, bbl/SCF
Note that Equation 5.54 for gas is identical to Equation 4.66 from Lesson 4 for oil with the exception that the original-gas-in-place, , replaces the original-oil-in-place, .

When we include additional derive mechanisms into our material balance equation, we can rewrite Equation 5.54 as:
This equation is identical to Equation 4.67 from Lesson 4 for oil reservoirs with the exception that the original-gas-in-place is substituted for the original-oil-in-place. The entries in Equation 5.55 are listed in Table 5.02.
| Term | Description |
|---|---|
| Total volume of withdrawal (production) at reservoir conditions in bbl | |
| Cumulative gas production in bbl | |
| Cumulative water production in bbl | |
| Total expansion in the reservoir in bbl/SCF | |
| Total expansion of the gas, bbl/SCF | |
| In over-pressured reservoirs, the expansion of the water and rock may add appreciable energy to the system, dimensionless | |
| If the reservoir is connected to an active aquifer, then once the pressure drop is communicated throughout the reservoir, the water will migrate into the reservoir resulting in a net water encroachment, We, bbl |
Where:
- is the original-gas-in-place, SCF
- is the gas production, SCF
- is the initial gas phase formation volume factor averaged over the reservoir, bbl/SCF
- is the gas phase formation volume at a future time averaged over the reservoir, bbl/SCF
- is the net rock volume, bbl
- is the current porosity averaged over the reservoir, fraction
- is the irreducible water saturation averaged over the reservoir, fraction
- is the water compressibility, 1/psi
- is the rock pore-volume compressibility, 1/psi
- is the current pressure averaged over the reservoir, psi
- is the current pressure averaged over the reservoir, psi
Since Equation 5.55 is a direct counterpart to the oil material balance equation, all of the analysis techniques discussed in Lesson 4 for oil reservoirs are applicable to gas reservoirs.
5.5.2: Field and Well Performance of Gas Reservoirs with Arps Decline Curve Analysis
Since decline curve analysis is an empirical curve fitting / trend-line technique, it can also be used for gas reservoirs with no modifications. We assume that the compressible nature of the gas is built into the established trends. When using Arps[2] Decline Curves, the same assumption applies for gas reservoirs: whatever processes that occurred in the past that helped to establish the trend of the data must continue to occur into the future.
As with oil reservoirs, decline curves for gas reservoirs can be used to make reservoir or well forecasts in both the time and domains, estimate the economic cumulative production from the reservoir or well (given the economic abandonment rate), and estimate the EUR (no economic limit) from the reservoir or well.
[2] Arps, J. J.: “Analysis of Decline Curves,” SPE-945228-G, Trans. of the AIME (1945)
5.6: Key Learnings
- Three of the key tasks performed by reservoir engineers working on a natural gas accumulation are the estimation of the Original-Gas-in-Place, OGIP, in a gas accumulation, the estimation of the stabilized production rate from a vertical production well, and the forecasting of future performance of a gas reservoir or well.
- These tasks have analogs with crude oil reservoirs, but there are significant differences between the methods used to analyze gas reservoirs due to the highly compressible nature of natural gas
- Two common methods for calculating the OGIP in a gas accumulation are:
- The Volumetric Method
- The Material Balance Method
- There are four drive mechanisms in a gas reservoir:
- Gas expansion (most significant drive mechanism in conventional gas reservoirs)
- Gas desorption (may only be present in certain unconventional gas reservoirs)
- Rock and fluid expansion (expansion of the reservoir rock and interstitial water – typically only significant in over-pressured gas reservoirs)
- Natural aquifer drive (or water encroachment)
- The major flow regimes experienced by vertical gas production wells are identical to those experienced by vertical oil production wells. These flow regimes are:
- Well dominated flow
- Transient flow
- Late transient flow
- Boundary dominated flow
- The stabilized production rates from a gas production well occur during the boundary dominated flow regime. These stabilized production rates are governed by the inflow performance relationships.
- The stabilized inflow performance of gas wells and the transient performance of gas wells can be estimated with three formulations. These formulations are based on the manner in which the term, , is integrated. These three formulations are:
- Pressure Formulation: valid for
- Pressure-Squared Formulation: valid for
- Pseudo-Pressure Formulation: valid for all pressures
- The Pseudo-Pressure Formulation is the most rigorous formulation within any pressure range of interest (even if another formulation is valid in that pressure range)
- Two common methods for making future reservoir or well forecasts for gas accumulations are:
- The Material Balance Method
- Decline curve analysis
- Exponential decline
- Hyperbolic decline
- Harmonic decline
5.7: Summary and Final Tasks
Summary
In this lesson, we discussed three very important tasks performed by reservoir engineers working on natural gas reservoirs. These tasks are identical to those performed by reservoir engineers working on oil reservoirs. These are:
- estimation of the Original-Gas-In-Place or OGIP;
- estimation of the stabilized production rate from a vertical gas well; and
- forecasting the future performance of gas reservoir and wells.
We saw that there were two methods commonly used in the oil and gas industry estimating the OGIP:
- the Volumetric Method
- the Material Balance Method
We also discussed that of these two methods, the material balance method is typically assumed to be more accurate as it is based on dynamic data.
We discussed the four Drive Mechanisms associated with gas reservoirs:
- gas expansion (most significant drive mechanism in conventional gas reservoirs)
- gas desorption (may only be present in certain unconventional gas reservoirs)
- rock and fluid expansion (expansion of the reservoir rock and interstitial water – typically only significant in over-pressured gas reservoirs)
- natural aquifer drive (or water encroachment)
We saw that the gas desorption mechanism is only applicable for unconventional gas reservoirs with significant organic content in the rock. The criteria of high organic content in the rock is normally met in:
- coal seam methane reservoirs
- shale gas reservoirs
We also discussed the stabilized production rates from vertical gas production wells. We saw that there were several flow regimes possible in a hydrocarbon reservoir (both natural gas and crude oil) that occurred at different stages in a well’s productive life. In Figure 4.06 from Lesson 4, we saw that these flow regimes occurred sequentially as the pressure disturbance caused by production propagates outward from the well towards the boundaries. These flow regimes are:
- Well dominated flow
- Wellbore storage
- Damage/Stimulation
- Transient flow
- Late transient flow
- Boundary dominated flow
- Steady-state
- Pseudo steady-state
In both gas and oil wells, the initial well dominated flow regime is controlled by well properties and well damage/stimulation, not reservoir properties. The transient flow regime is governed by the diffusivity equation and is characterized by time dependent rates and/or pressures. The onset of the late transient period occurs when the pressure disturbance from the production well reaches the first boundary of the drainage volume. The end of the late transient period occurs when the pressure disturbance reaches the last boundary of the drainage volume. The boundary dominated flow regime is the last flow regime experienced by the well. Stabilized production occurs during the boundary dominated flow period and is described by one of the Inflow Performance Relationships, IPRs that we derived in this lesson.
In natural gas wells, three different formulations can be used to develop the stabilized IPRs and the transient diffusivity equation. These formulations are based on the manner in which the term, , is integrated in the development of the different equations. These three formulations are:
- Pressure Formulation: valid for
- Pressure-Squared Formulation: valid for
- Pseudo-Pressure Formulation: valid for all pressures
The Pseudo-Pressure Formulation is the most rigorous formulation within any pressure range of interest (even if another formulation is valid in that pressure range).
For forecasting future reservoir or well performance, we discussed two methods: Material Balance Analysis and Decline Curve Analysis. In the Material Balance Method, we needed to modify the governing equations from their oil counterparts to account for the highly compressible nature of gas. We did this by incorporating the Real Gas Law into the equations rather than the definition of a slightly compressible fluid (note, water and its expansion in a gas reservoir are still treated as slightly compressible). For Decline Curve Analysis, we did not need to make any modifications to the Arps[2] [55] Equations.
Final Tasks
Complete all of the Lesson 5 tasks!
You have reached the end of Lesson 5! Double-check the to-do list on the Lesson 5 Overview page [56] to make sure you have completed all of the activities listed there before you begin Lesson 6.
Lesson 6: Production Engineering: Flow in Well Tubing
6.0: Lesson Overview
You will have two weeks to complete Lesson 6.
Lesson 6 is very extensive, and you will have two weeks to read through the lesson and complete the associated assignments. Please use your time wisely and don't let yourself fall behind; you will need the extra week to work your way effectively through the material.
Please refer to the Calendar in Canvas for specific time frames and due dates.
In this lesson, we will discuss fluid flow in the oil and gas wells. Production Engineers are concerned with optimizing production from a given well. Well Modeling is a tool that allows production engineers to determine production rates and pressure drops in a well. This allows the engineer to identify bottlenecks in the production system (reservoir, tubing, well head) and seek methods to alleviate these bottlenecks (debottleneck the well).
Production engineers use tubing calculations and well modeling during all phases of the well’s productive life - from designing the initial completion to developing well intervention strategies as conditions in the reservoir change (pressure and saturations).
Learning Objectives
By the end of this lesson, you should be able to:
- list and understand the different well orientations used to produce crude oil and natural gas;
- describe the basics of tubing hydraulics (fluid flow in well tubing) during crude oil and natural gas production;
- state the physical parameters that impact pressure losses in well tubing;
- discuss the different flow regimes that can occur in vertical and horizontal flow through well tubing;
- explain the concept of the energy balance and how it relates to tubing hydraulics and the Darcy-Weisbach Equation;
- explain the concept of friction losses in well tubing and understand the factors that control frictional losses during production and injection;
- identify the equations that can be used to estimate the pressure drop in single-phase liquid and gas flow;
- perform tubing hydraulics calculations for single-phase liquid and gas flow;
- describe the differences between a Pressure Traverse Calculation and a Tubing Performance Calculation for single-phase and multi-phase flow;
- list and describe the static and dynamic data considered in tubing hydraulics calculations;
- describe the concept of a flow pattern map and how these maps are incorporated into multi-phase tubing hydraulics calculations; and
- list the different multi-phase flow correlations used in the oil and gas industry and their applications.
Lesson 6 Checklist
| To Read | Read the Lesson 6 online material | Click the Introduction link below to continue reading the Lesson 6 material |
|---|---|---|
| To Do | Lesson 6 Quiz | Take the Lesson 6 Quiz in Canvas |
Please refer to the Calendar in Canvas for specific time frames and due dates.
Questions?
If you have questions, please feel free to post them to the Course Q&A Discussion Board in Canvas. While you are there, feel free to post your own responses if you, too, are able to help a classmate.
6.1: Introduction
In earlier lessons, we learned that production engineers are tasked with optimizing the production or injection from individual wells. This optimization involves monitoring the well to determine if its performance can be improved; stimulating the well with acidizing or hydraulic fracturing if there is well damage; applying artificial lift (gas lift or pumps) to improve the economics of low rate wells; performing well workovers to shut-off excess gas or water production; along with many other types of well interventions.
In order to understand how wells are performing, we must first understand the tubing hydraulics (flow behavior in production or injection wells). For this, we need an introduction to modern oil and gas wells and a brief description of the nature of the problem to be solved.
6.2: Introduction to Gas and Liquid Flow through Well Tubing
In oil and gas production, Tubing is the pipe or conduit where fluids are transported from the reservoir to the surface. This is shown Figure 6.01. Figure 6.01 shows the Wellbore Schematic for a typical vertical well. This figure is a schematic cross-section through the axis of the well. This schematic shows two types of pipe, casing and tubing. The casing is used and installed during the drilling process, and we will discuss the purpose of the casing when we discuss the drilling process in Lesson 8. For now, we are interested in the tubing.
The tubing is the inner most string of pipe in the well. As I stated, this is the conduit that connects the reservoir to the surface. Reservoir fluids flow from the reservoir, through the perforations, into the tubing, and the up the well. In this well schematic, fluids are prevented from flowing through the Annular Space between the tubing and Production Casing String with a Packer (a packer is a device that seals the annular space between the production casing and tubing and mechanically prevents fluids from flowing through the annulus). It is the tubing that will be the focus of this lesson.

Wells drilled for oil and gas production (or fluid injection) are not always straight, vertical wells. Wells can be designed to be straight, deviated, or horizontal. This is shown in Figure 6.02 for three common well types: vertical wells, deviated wells, and horizontal wells. In addition to wells that were planned to be deviated, wells that were planned to be straight, vertical wells often deviate from the true vertical direction during the drilling process.

In the field, the measurement of the three-dimensional path of a well is called a Directional Survey. A directional survey can be performed with either magnetic or gyroscopic instrumentation. The data recorded during a directional survey include:
- the True Vertical Depth, TVD
- the Measured Depth, MD
- the well inclination from the vertical (0° for a vertical well and 90° for a horizontal well). Note, for our flow calculations, we will use inclination from the horizontal
- the well direction N-S-E-W or 0 - 360°)
The objectives of the directional survey are to:
- determine the exact bottom-hole location;
- monitor the well’s progress during drill to ensure the well will reach the intended target;
- orient the deflection of any tools run in the well to ensure tools can traverse the well path;
- establish the relationship of TVD and MD for in support of well logging and wellbore hydraulics modeling; and
- calculate the TVD of various geologic formations to allow for proper geological mapping.
Figure 6.02 depicts three wells. In this figure, the Kelly Bushing is the mechanical assembly that rotates on the rig floor causing the drill pipe and drill bit to rotate. We will learn much more about the Kelly Bushing in Lesson 8. The Kelly Bushing (and, essentially, the rig floor) is a common reference point for depths/lengths in a well. This figure shows four common measurements used in the oil and gas industry for the well lengths and depths:
- TVD: True Vertical Depth is the depth (or length) in the true vertical direction measured from the Kelly Bushing to the point of interest.
- TVD ss: True Vertical Depth sub-sea is the depth (or length) in the true vertical direction measured from the mean sea level to the point of interest.
- MD: Measured Depth is the path length of the depth (or length) measured from the Kelly Bushing to the point of interest.
- KBE: The Kelly Bushing Elevation is the elevation of the Kelly Bushing measured from the sea level.
As we will see, these measurements can have a significant impact on the tubing hydraulics once the well is put onto production or injection. For example, gravity (and hydrostatic pressure) and the geothermal gradient will act in the true vertical direction (TVD), while friction will act along the total length of the tubing (MD).
As oil enters the well and begin flow upwards several Flow Regimes or Flow Patterns can occur in the tubing. These flow patterns in vertical flow are shown in Table 6.01.
| Vertical Cross-section | Description |
|---|---|
 |
Mist Flow:
|
Annular Flow:
|
|
Churn Flow:
|
|
Slug Flow:
|
|
Bubble Flow:
|
|
Single-Phase Flow:
|
|
| Image by Greg King © Penn State, is licensed under CC BY-NC-SA 4.0 [57] | |
When crude oil first enters the well and tubing, it may be above its bubble-point pressure (note, if the reservoir is below the bubble-point pressure, then free gas will enter the well and tubing and a more continuous gas phase will be present in the base of the tubing near the perforations). As the liquid flows up the tubing, pressure is expended as a pressure differential is required to lift the liquid column to the surface.
At some point, the pressure falls below the bubble-point pressure in the tubing, and gas begins to come out of solution. As we discussed in Lesson 2, crude oils and natural gases are complex mixtures hydrocarbon molecules. Figure 6.03 is a Phase Diagram for an undersaturated oil reservoir (crude oil above its bubble-point pressure). In Lesson 4 and Lesson 5, we discussed the behavior of the crude oil and natural gas in the reservoir. This is the solid p-T path shown in Figure 6.03: Path (, ) to (, ).
The dashed p-T path in Figure 6.03 is the path that the fluids take going from the reservoir to the surface separator. Remember, we have seen in Lesson 4 and Lesson 5 that in the reservoir as we remove fluids, the reservoir pressure is reduced. Therefore, the starting point for the path to the separators, Path (, ) to (, , will be the time-dependent current reservoir pressure,

As fluids travel up the well along the dashed path in Figure 6.03, we can see that the tubing flow is a non-isothermal process; the temperature of the flowing fluid changes due to the local geothermal gradient. This has several implications in the tubing hydraulics process. For example, as we see in Figure 6.03, the bubble-point pressure (the pressure where the path enters the two-phase region) for the solid reservoir path, Path (, ) to (, ), is different from the bubble-point pressure for the dashed tubing path, Path (, ) to (, ). It is the bubble-point pressure along the dashed path that results in the onset of the bubble flow pattern shown in Table 6.01.
As flow continues up the tubing in Table 6.01, the pressure continues to fall causing gas bubbles to expand due to the compressible nature of gas and solution gas to come out of solution. As the gas bubbles expand, they begin to coalesce and form gas slugs in the center of the tubing. Due to buoyancy, the gas slugs travel at a higher velocity than the liquid and begin to push the liquid up the tubing.
As flow continues up the tubing, the gas slugs continue to expand and begin to form a continuous phase in the center of the tubing. This is the churn flow pattern shown in Table 6.01. During churn flow, high velocity gas pushes liquids up the well, but liquid tends to slip back downward due to its density. As flow continues upward, the continuous gas phase pushes the liquid up the tubing with gas flowing rapidly in the center of the tubing and the liquid flowing slower in the annular space between the tubing walls and the continuous gas phase. This is the annular flow pattern shown in Table 6.01.
As gas and liquid continue to flow upward, the gas phase expands further, leaving less room on the tubing walls for the liquid. During this flow regime, liquids are pushed upwards in liquid slugs and as mist entrained in the gas.
We should remember that not all of these flow regimes occur in all wells. The flow regimes occurring in the tubing will be determined by the conditions in the well. For example, if an undersaturated crude oil reservoir is being produced and the wellhead pressure, , is kept above the surface bubble-point pressure, then the well will only flow in the single-phase flow regime.
As we can see from Figure 6.02, wells can be planned and executed as deviated (or slanted) wells and as horizontal wells. Flow through the tubing in the horizontal section of a well has distinct flow patterns. These flow patterns are illustrated in Table 6.02.
| Cross-Section | Longitudinal-Section | Description |
|---|---|---|
 |
 |
Single-Phase Flow:
|
 |
 |
Bubble Flow:
|
 |
 |
Plug Flow:
|
 |
 |
Stratified Flow:
|
 |
 |
Wavy Flow:
|
 |
 |
Slug Flow:
|
 |
 |
Annular Flow:
|
 |
 |
Spray Flow:
|
|
Source: All images by Greg King © Penn State, licensed under CC BY-NC-SA 4.0 [57]
|
||
Referring to Table 6.02, as with vertical tubing, if oil enters the horizontal tubing above the bubble-point pressure, then flow will be single-phase and the liquid will be transported in the Single-Phase Flow Regime. As pressure travels horizontally, the pressure differential required to transport the liquid may cause the pressure to drop below the bubble-point pressure of the oil. When this occurs, the tubing fluids enter the Bubble Flow Regime (B). As pressure drops further due to liquid transport, the bubbles expand and coalesce to form gas plugs. When this occurs, the gas and liquid enter the Plug Flow Regime (C). As pressures continue to drop, the gas plugs continue to expand and coalesce, eventually forming a continuous gas phase. If the phase velocities are low, then gravity will act to segregate the phases vertically. This is the Segregated Flow Regime (D). In the segregated flow regime, the surface between the two phases is relatively smooth. If velocities are higher, then the surface of the two segregated phases may develop waves and ripples. This is the Wavy Flow Regime (E). If the velocities are greater still, then the height of the waves may reach the top of the tubing, temporarily closing off the cross-section to the flow of gas. This is the Slug Flow Regime (F). The slug flow regime results in very unstable flow because of the differences in the momentum between the gas and liquid phases due to the different densities and different phase velocities. When the cross-section is cut off to the gas phase, its momentum must be transferred to the liquid phase. At higher velocities, gravity acts too slow to segregate the phases and the flow may enter the Annular Flow Regime (G). In this flow regime, the continuous gas phase occupies the center of the tubing, while liquid phase forms an annular ring between the gas phase and the tubing wall. While gravity may be too slow to create complete vertical segregation, the less dense gas phase may flow higher in the tubing (i.e., the gas and oil may flow in a non-concentric manner). Finally, if the velocity is very high, the gas may occupy most of the cross-section and liquid is transported as a mist that is entrained in the gas. This occurs in the Spray Flow Regime (H). Spray flow is a very stable flow regime with the liquid and gas phases traveling at comparable velocities.
These are the basic flow regimes that can occur in vertical and horizontal tubing. We will revisit these flow regimes when we discuss Multi-Phase Tubing Performance later in this lesson.
6.3: Tubing/Pipe Calculations
6.3: Tubing/Pipe Calculations section of this lesson will cover the following topics and sub-topics:
- 6.3.1: Equations Governing Flow in Pipe and Tubing [58]
- 6.3.2: Single-Phase Flow of Liquids in Tubing [59]
- 6.3.2.1: The Darcy-Weisbach Equation for Single-Segment Oil Production Wells [60]
- 6.3.2.2: The Darcy-Weisbach Equation for Segmented Oil Production Wells [61]
- 6.3.2.3: The Darcy-Weisbach Equation for Segmented Injection Wells [62]
- 6.3.2.4: The Hazen-Williams Equation for Liquid Production/Injection Wells [63]
- 6.3.3: Single-Phase Flow of Gases in Tubing [64]
- 6.3.4: Multi-Phase Flow [67]
6.3.1: Equations Governing Flow in Pipe and Tubing
Bernoulli’s Equation
Bernoulli’s Equation forms the basis of the steady-state tubing performance. Bernoulli’s Equation is simply an energy balance on a given system. In our case, that system is the production tubing. Bernoulli’s Equation can be written as:
In this equation, all of the terms have the units of lbf-ft. The variables in this equation are:
- and are the Internal Energies stored in the fluid at two points in the system, lbf-ft. This internal energy is energy at the molecular level and cannot be measured in an absolute sense. We can establish the relative change in the internal energy () by assigning a zero value at some specific set conditions.
- and are the pressures at two points in the system, psi
- and are the volumes of the fluid at two points in the system, ft3
- The terms and are the Energies of Expansion or Compression, lbf-ft. These terms represent compressional energy stored in the fluid (similar to the energy stored in a compressed spring).
- is the mass of the fluid in the system, lbm
- and are the velocities of the fluid at two points in the system, ft/sec
- is the Universal Gravitational Constant, 32.174 lbm-ft/lbf-sec2
- The terms and are the Kinetic Energy of the fluid in the system, lbf-ft
- is the Local Acceleration due to gravity, ft/sec2. The local acceleration due to gravity varies from location to location but is approximately equal to 32.174 ft/sec2. The ratio of is approximately equal to 1.0 lbf/lbm.
- and are elevations above some reference point, typically sea level, ft
- The terms and are the Potential Energies of the fluid at two points in the system, lbf-ft
- is the Thermal Energy added to or removed from the system, lbf-ft. In Equation 6.01, is positive if thermal energy is added to the system or negative if thermal energy is removed from the system (note: 1 BTU = 778.169 lbf-ft)
- is the work added to or performed by the fluid, lbf-ft. In Equation 6.01, is positive if work is added to the system (for example, with a pump) or negative if work is removed from the system (for example, by turning a turbine)
There are many engineering Thermodynamics concepts in this equation which are out-of-scope for this course; however, we can illustrate the application of Bernoulli’s Equation in the context of flow through tubing with Figure 6.04.

In Figure 6.04, we have a length of vertical tubing defined from a depth of to a depth of with an inner diameter of . A mass of oil enters the tubing at at a volumetric rate of (ft3/sec) at a pressure of and a velocity of . As the oil travels up from the reservoir, the surrounding rock is cooler than the oil due to the local geothermal gradient, and heat is lost () from the hot oil to the surrounding cooler rock. Flowing upward, the oil encounters a downhole pump which supplies work () to the system. The oil finally reaches point in the tubing with a Terminal Pressure of and Terminal Velocity of .
Without going into the thermodynamic details, Equation 6.01 can be rewritten in differential form as:
Where:
and,
- is the pressure at a point in the tubing, psi
- is the distance along the axis of the tubing, ft
- 144 is a unit conversion constant, in2/ft2
- 12 is a unit conversion constant, in/ft
- is the Universal Gravitational Constant, 32.174 lbm-ft/lbf-sec2
- is the Local Acceleration due to gravity, ft/sec2. The local acceleration due to gravity varies from location to location but is approximately 32.174 ft/sec2. The ratio of is approximately 1.0 lbf/lbm
- is the angle of inclination above the horizontal, dimensionless
- is the Darcy-Weisbach Friction Factor, dimensionless
- is the velocity of the fluid at the point in the tubing, ft/sec
- is the density of the fluid, lbm/ft3
- is the Inner Diameter () of the tubing, in
- is the elevation of the point in the tubing above a reference point, typically sea level, ft
The units of each of the terms in Equation 6.02 and Equation 6.03 are psi/ft. The well orientation for Equation 6.02 and Equation 6.03 is shown in Figure 6.05.

In Equation 6.02, I have neglected the Heat Transfer, , and Work, , terms. If we have significant heat transfer or a device that adds or performs work, we can include these terms into the equation.
Expanding on the terms in Equation 6.02, the elevation term, , is simply the change in the potential energy as the fluid flows through the tubing in the direction of . Note that in the convention shown in Figure 6.05 with the z-direction upward, point has a higher potential energy than point because it has a higher elevation. The friction term, , is the irreversible loss of energy due to friction as the fluid flows past the stationary tubing wall. Friction always acts in the direction of opposite of flow. For single-phase flow, the only friction component occurs at the liquid-tubing interface. In multi-phase flow where phases are flowing at different velocities, there will be a friction component occurring at the phase boundaries also. Finally, the acceleration term, , is the change in energy resulting from the acceleration or deceleration of the fluid going around bends in the tubing. The acceleration term is often neglected in tubing calculations.
As mentioned earlier, the friction factor, fDW, in Equation 6.03b is the Darcy-Weisbach friction factor. This equation is co-credited to Henry Darcy, who is the same Darcy that gave us Darcy’s Law. The Darcy-Weisbach friction factor is the ratio of the shear stress at the wall and the kinetic energy of the fluid on a unit volume basis. This friction factor was plotted by Moody[1]as a function of the Reynolds Number[2],[3], , and the Relative Roughness . The Moody Diagram is shown in Figure 6.06.
Note, we will be using the Darcy-Weisbach friction factor, , which is not to be confused with the Fanning Friction Factor, [4]. The Fanning friction factor is ¼ the value of the Darcy-Weisbach friction factor, that is: . The difference between the two friction factors is that the Darcy-Weisbach friction factor is typically used for closed circular pipes, and uses as the diameter, while the Fanning friction factor can be used for open conduits and uses the concept of the “hydraulic radius” as a measure of the diameter: . Where is the hydraulic radius, is the cross-sectional area of flow (length squared), and is the “wetted perimeter” (length). The wetted perimeter is the perimeter of the cross-section in contact with the conduit (portion of the cross-section that is “wetted” by the fluid).
The Reynolds Number, , is a dimensionless group that represents the ratio of the inertial forces to the viscous forces within the fluid and is used to characterize laminar and turbulent flow regimes. For our application of flow through pipe, the Reynolds Number is defined by:
Where:
- is the Reynolds Number, dimensionless
- 1488.0 is a unit conversion constant, ft-sec-cp/lbm
- 12 is a unit conversion constant, in/ft
- 124 in an equation constant
- is the Inner Diameter ( ) of the tubing, in
- is the velocity of the fluid in the tubing, ft/sec
- is the density of the fluid, lbm/ft3
- is the dynamic viscosity of the fluid, cp
Note, Equation 6.04a can be expressed in an equivalent form in terms of flow rate, :
Where the velocity term was replaced with the rate term: .
At lower values of flow is in the laminar flow regime, while at higher values of flow is in the turbulent flow regime. As we see in the Moody Diagram, Figure 6.06, in the turbulent flow regime the friction factor is a function of the Reynolds Number and relative roughness of the pipe . The relative roughness is a dimensionless quantity that is defined as the length of protrusions (lumps, pipe defects and imperfections, pits from corrosion, etc.) divided by the inner diameter of the tubing. It is a measure of the departure of an actual steel pipe from an idealized, smooth pipe. Figure 6.07 illustrates the concepts of absolute and relative roughness, while Table 6.03 shows typical values of the absolute roughness, , for different materials.

In the laminar flow regime , the Darcy-Weisbach friction factor is a function of the Reynolds Number only and can be determined by:

| Material | ||
|---|---|---|
| Idealized smooth surface – any material | 0.0 | 0.0 |
| Concrete – coarse | 0.2500 | 0.009842 |
| Concrete – new smooth | 0.0250 | 0.000984 |
| Drawn tubing | 0.0025 | 0.000098 |
| Glass, Plastic Perspex | 0.0025 | 0.000098 |
| Iron – cast | 0.1500 | 0.005906 |
| Sewers – old | 3.0000 | 0.118110 |
| Steel – mortar lined | 0.1000 | 0.003937 |
| Steel – rusted | 0.5000 | 0.019685 |
| Steel – structural or forged | 0.2500 | 0.009842 |
| Water mains – old | 1.0000 | 0.039370 |
As previously discussed, in the turbulent flow regime, the Darcy-Weisbach friction factor is a function of both the Reynolds Number and the relative roughness. To calculate the friction factor in the turbulent regime, the Implicit Colebrook Equation[6] can be used:
We say that this equation is implicit because the friction factor, , appears on both sides of the equals sign. Therefore, to solve this equation, we must iterate on a solution. That is, we make an initial guess at and use it on the right-hand side of the equation to calculate a new on the left-hand side of the equation. We repeat this process until the two values of (the recently calculated value on the left-hand side of the equation and the value used in the calculation on the right-hand side of the equation) are sufficiently close. To start the process, an Explicit Formula for , such as the Swamee-Jain Equation[7], is used:
We say that Equation 6.07 is an explicit formula because the friction factor does nor appear on the right-hand side of the equation, and we can solve for it explicitly. The Swamee-Jain Equation[7] is an approximation to the Colebrook Equation[6] and can also be used directly in calculations.
[1] Moody, L. F. (1944), "Friction factors for pipe flow", Transactions of the ASME, 66 (8): 671–684
[2] Stokes, George (1851). "On the Effect of the Internal Friction of Fluids on the Motion of Pendulums". Transactions of the Cambridge Philosophical Society. 9: 8–106.
[3] Reynolds, Osborne (1883). "An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels". Philosophical Transactions of the Royal Society. 174 (0): 935–982.
[4] Fanning, J. T. (1877). A practical treatise on water-supply engineering, Van Nostrand, New York, 619
[6] Colebrook, C. F. (1938–1939). "Turbulent Flow in Pipes, With Particular Reference to the Transition Region Between the Smooth and Rough Pipe Laws". Journal of the Institution of Civil Engineers. London, England. 11: 133–156.
[7] Swamee, P.K., and Jain, A.K. (1976). Explicit equations for pipe flow problems. J. Hydraul. Div. ASCE 102 (HY5), 657–664.
6.3.2: Single-Phase Flow of Liquids in Tubing
6.3.2: Single-Phase Flow of Liquids in Tubing section of this lesson will cover the following topics:
- 6.3.2.1: The Darcy-Weisbach Equation for Single-Segment Oil Production Wells [60]
- 6.3.2.2: The Darcy-Weisbach Equation for Segmented Oil Production Wells [61]
- 6.3.2.3: The Darcy-Weisbach Equation for Segmented Injection Wells [62]
- 6.3.2.4: The Hazen-Williams Equation for Liquid Production/Injection Wells [63]
6.3.2.1: The Darcy-Weisbach Equation for Single-Segment Oil Production Wells
The Darcy-Weisbach Equation is one of the most common equations for modeling single-phase liquid flow through pipes and tubing. The Darcy-Weisbach Equation is developed by ignoring the acceleration term in Equation 6.02 and replacing the derivative with a finite-difference approximation:
Where the angle, , is measured from the horizontal and is 90º for true vertical wells and 0º for horizontal wells. Solving this equation for the velocity:
Substituting for the velocity term, :
or, after evaluating the constants and rearranging:
Noting that the term (the change in elevation over the length of the tubing, ):
This is the theoretically derived Darcy-Weisbach Equation for flow through pipe/tubing in oilfield units. This equation relates the flow rate, , to a given pressure drop . In practice, we include a dimensionless efficiency factor, , which is approximately equal to one . This efficiency factor is used to tune the equation to actual field measurements.
This version of the Darcy-Weisbach Equation is the version most often used in industry software. In this equation:
- 411.147 is an equation constant
- 144 is a unit conversion constant, in2/ft2
- is the flow rate through the tubing, bbl/day
- is an efficiency (tuning) factor for the tubing section , dimensionless
- is the Inner Diameter () of the tubing, in
- is the Universal Gravitational Constant, 32.174 lbm-ft/lbf-sec2
- is the Local Acceleration due to gravity, ft/sec2. The local acceleration due to gravity varies from location to location but is approximately 32.174 ft/sec2. The ratio of is approximately 1.0 lbf/lbm
- is the Darcy-Weisbach Friction Factor, dimensionless
- is the density of the fluid, lbm/ft3
- is the length of the section of tubing along its axis, ft
- and are the pressures at two points in a section of tubing, psi
- and are the elevations at two points in a section of tubing, psi
We can use this equation in two ways. The first way to use Equation 6.12, is to specify the flow rate and calculate the pressure drop along the section of the pipe/tubing. This calculation is called a Pressure Traverse calculation and is illustrated in Figure 6.08 for a vertical well. In this figure, two tubing diameters are considered, and multiple production rates are plotted for each tubing size. The pressure traverse calculation is used by production engineers to help select the appropriate tubing size for the anticipated well production rates during the completion design phase of the well.
Alternatively, if we know one pressure and the flow rate, then we can calculate the other pressure. This is normally done by specifying the Well Head Pressure, , and calculating the flowing bottom-hole pressure, , for multiple production rates. This is called Tubing Performance calculation and is illustrated in Figure 6.09 for a well head pressure of and the same two tubing sizes plotted in Figure 6.08: in and .
6.3.2.2: The Darcy-Weisbach Equation for Segmented Oil Production Wells
In our previous discussion, we assumed that properties, such as, viscosity and density (for use in the Reynolds Number calculation in Equation 6.04) or the density (for use in the Darcy-Weisbach Equation itself in Equation 6.12) were constant over the entire length of the pipe/tubing. As fluids flow up the vertical section of tubing, the pressure drop may cause changes in these properties for slightly compressible fluids. In addition, the upward flow of fluids in the vertical section of tubing is a non-isothermal process, and this may also cause changes in these properties as fluids flow upward. As already mentioned, in the extreme case, fluids may drop below the bubble-point pressure, resulting in multi-phase flow through multiple flow regimes (see Table 6.01). For these cases, Segmented Wells can be used.
Segmented wells are wells where the entire well length is partitioned into multiple, smaller well segments. The pressure drop along one segment is calculated using the local pressure and temperature conditions (assuming an appropriate heat transfer model is available). Once the calculations are performed for one segment of tubing, the Terminal Pressure (pressure at the outlet end of the tubing section - in Figure 6.04) is used as the starting pressure (or inlet pressure, ) for the next segment of the well.

In addition to fluid property changes during flow, there may be design reasons for using segmented wells. For example, the deviated and horizontal wells shown in Figure 6.02 will require the use of segmented wells: at least one segment for the non-vertical section of the tubing and at least one segment for the vertical section of the tubing. In addition, there may be reasons for designing a Tapered Tubing String (a tubing string with different inner diameter tubing sizes along different lengths of the well). These wells are designed to keep a desired flow velocity at different depths in the well.
The use of segmented wells for modeling well production is the most common method of modeling actual wells. Well modeling is a common activity for Production Engineers.

6.3.2.3: The Darcy-Weisbach Equation for Segmented Injection Wells
Injection Wells are required for Secondary and Tertiary Oil Production Methods. In secondary and tertiary production, fluids are pumped from the surface and injected into the reservoir. The most common secondary oil production method is Waterflooding. For the purpose of our discussion, this is relevant because the direction of the fluid is reversed in Figure 6.04 and Figure 6.05, resulting in a reversal of the signs in our equations. Therefore, for liquid injection wells, the Darcy-Weisbach Equation becomes (note sign change):
6.3.2.4: The Hazen-Williams Equation for Liquid Production/Injection Wells
In addition to the Darcy-Weisbach Equation for liquid production/injection wells, the Hazen-Williams Equation also has applications in the oil and gas industry (most commonly for injection wells, but also valid for light hydrocarbon liquids). The Hazen-Williams Equation is an Empirical Method (based on observations, not theory) which pre-dates the Darcy-Weisbach Equation. It was used in times prior to the widespread use of computers due to its simplicity, as it does not include a friction factor. The Hazen-Williams formula replaces the general friction factor with a material specific constant, , and modifies the equation constant and exponents. The Hazen-Williams Equation in oilfield units is:
In this equation:
- 15.2 is an equation constant
- 144 is a unit conversion constant, in2/ft2
- is the sign convention used in the equation with “ ” for production or “ ” for injection
- is the flow rate through the tubing, bbl/day
- is the Hazen-Williams (tuning) Factor for the tubing section , dimensionless
- is the Inner Diameter ( ) of the tubing, in
- is the Universal Gravitational Constant, 32.174 lbm-ft/lbf-sec2
- is the Local Acceleration due to gravity, ft/sec2. The local acceleration due to gravity varies from location to location but is approximately 32.174 ft/sec2. The ratio of is approximately 1.0 lbf/lbm
- is the density of the fluid, lbm/ft3
- is the length of the section of tubing along its axis, ft
- and are the pressures at two points in a section of tubing, psi
- and are the elevations at two points in a section of tubing, psi
Note in the Hazen-Williams Equation, that we have replaced the efficiency factor, , with the Hazen-Williams Factor, , and removed the friction factor, (in addition to modifying the constant and exponents). Typical values of for different materials are listed in Table 6.04. While the Hazen-Williams Factor is not an efficiency factor; in practice, it is used in much the same way as in the Darcy-Weisbach Equation: to tune the equation to match field measured data.
The computational simplicity of the Hazen-Williams Equation now becomes apparent – there is no need for the Reynolds Number and friction factor calculations. These calculations are included implicitly in the empirical Hazen-Williams Factor and the modified exponents. As mentioned earlier, the Hazen-Williams Equation is valid for water and light hydrocarbons, such as, gasoline and possibly condensates.
| Material | Minimum Value | Maximum Value |
|---|---|---|
| Polyvinyl chloride (PVC) | 150 | 150 |
| Fiber reinforced plastic (FRP) | 150 | 150 |
| Polyethylene | 140 | 140 |
| Cement, Mortar Lined Ductile Iron Pipe | 140 | 140 |
| Asbestos, cement | 140 | 140 |
| Copper | 130 | 140 |
| Cast iron – new | 130 | 130 |
| Galvanized iron | 120 | 120 |
| Cast iron – 10 years | 107 | 113 |
| Concrete | 100 | 140 |
| Steel | 90 | 110 |
| Cast iron – 20 years | 89 | 100 |
| Cast iron – 30 years | 75 | 90 |
| Cast iron – 40 years | 64 | 83 |
[8] Wikipedia: Hazen–Williams Equation [70]
6.3.3: Single-Phase Flow of Gases in Tubing
6.3.3: Single-Phase Flow of Gases in Tubing section of this lesson will cover the following topics:
6.3.3.1: The Darcy-Weisbach Equation for Gas Production Wells
The Darcy-Weisbach Equation for natural gases can be developed by modifying the equation for liquids using a simple change of units. For standard oilfield units:
or,
Note, this equation assumes that the flow rate, , is in ft3/day; however, it can easily be re-written in M ft3/day or MM ft3/day by adjusting the equation constant, 2,308.59, to either 2.30859 or 2.30859x10-3, respectively. In this equation:
- 411.147 is an equation constant
- 5.615 is a unit conversion constant, ft3/bbl
- Equation constant:
- 2,308.59 (for ft3/day)
- 2.30859 (for M ft3/day)
- 2.30859 x10-3 (for MM ft3/day)
- 144 is a unit conversion constant, in2/ft2
- is the sign convention used in the equation with “ ” for production or “ ” for injection
- is the flow rate through the tubing, ft3/day, M ft3/day, or MM ft3/day
- is an efficiency (tuning) factor for the tubing section, dimensionless
- is the Inner Diameter ( ) of the tubing, in
- is the Universal Gravitational Constant, 32.174 lbm-ft/lbf-sec2
- is the Local Acceleration due to gravity, ft/sec2.
- is the Darcy-Weisbach Friction Factor, dimensionless
- is the density of the fluid, lbm/ft3
- is the length of the section of tubing along its axis, ft
- and are the pressures at two points in a section of tubing, psi
- and are the elevations at two points in a section of tubing, psi
In Lesson 3, we saw that the density of a real gas could be determined by the Real Gas Law (Equation 3.71):
Due to the strong dependence of the gas density on local pressure and temperature, the solution of Equation 6.15b is always performed using the segmented well approach with iterations on the outlet pressure, . Essentially, the segmented well approach explicitly performs a numerical integration of the differential energy balance equation, Equation 6.08 (in terms of ). The steps for this simple iteration are:
- Assume a fixed length, , of tubing (usually in the range of 100 – 200 ft)
- Calculate the temperature (in ºR) halfway up the tubing length using the local temperature gradient in ºR/ft (feet in true vertical depth, )
- Start with the known inlet pressure,
- Assume an outlet pressure,
- Calculate the average pressure in the length of tubing,
- Calculate the Z-Factor and gas density from Equation 6.16 with the temperature from Step 2 and the average pressure from Step 5
- Evaluate the Reynolds Number from Equation 6.04 using this gas density (viscosity may also change with temperature)
- Calculate the Darcy-Weisbach Friction Factor from the Moody Diagram (Figure 6.06), the Colebrook Formula[6] (Equation 6.06), or the Swamee-Jain Equation[7] (Equation 6.07) using the Reynolds Number from Step 7
- Apply the Darcy-Weisbach Equation, Equation 6.15b, to calculate a new outlet pressure,
- Go to Step 5 and continue calculations until two successive iterations of agree to a specified tolerance
- When converged, proceed to the next length of tubing and start from Step 10
6.3.3.2: Other Equations for Gas Production Wells
As seen with this iteration, the use of the Darcy-Weisbach Equation can result in very complicated iteration process and requires the use of a computer for a solution. There are other methods available for gas wells and pipelines that can also be used that do not require an iteration.
One popular method used for gas wells is the Cullender and Smith[9] Method. This method uses a limited range of the relative roughness of 0.0006 to 0.00065 and a specialized friction factor correlation designed specifically for this range (not the generalized Colebrook Formula[6] or the Swamee-Jain Equation[7]). In addition, the method uses a two-step integration based on the trapezoid rule (two well segments). This method also requires an iteration, but it is not as complex as that shown above.
Other popular methods for gas wells and transmission lines include the Weymouth equation, the Panhandle “A” equation, and the Panhandle “B” equation. These equations are empirical equations developed from the generalized energy balance equation but use specialized, explicit friction factor correlations which allow them to be solved in a non-iterative manner. Also note that these equations use the flow rate in SCF/day and not ft3/day as in Equation 6.15. These equations have the form:
with
Where:
- is an equation constant:
- 433.5 (for the Weymouth equation)
- 435.87 (for the Panhandle “A” equation)
- 737.0 (for the Panhandle “B” equation)
- 0.0375 is an equation constant
- 5280.0 is a unit conversion constant, ft/mile
- is the flow rate through the tubing, SCF/day
- is an efficiency (tuning) factor for the tubing section , dimensionless
- is the Inner Diameter of the tubing, in
- is the standard temperature, ºR
- is the standard pressure, psi
- and are the pressures at two points in a section of tubing, psi
- is the specific gravity of the gas, , dimensionless
- is the real gas supercompressibility factor (Z-Factor), dimensionless
- is the average temperature of the tubing section, ºR
- is the length of the section of tubing along its axis, ft
- is a correction factor for change in elevation, dimensionless
- and are the elevations at two points in a section of tubing, ft
- is the angle from the horizontal, degrees or radians
- is an exponent:
- 2.667 (for the Weymouth equation)
- 2.6182 (for the Panhandle “A” equation)
- 2.530 (for the Panhandle “B” equation)
- is an exponent:
- 1.0 (for the Weymouth equation)
- 1.0788 (for the Panhandle “A” equation)
- 1.02 (for the Panhandle “B” equation)
- is an exponent:
- 1.0 (for the Weymouth equation)
- 0.853 (for the Panhandle “A” equation)
- 0.961 (for the Panhandle “B” equation)
- is an exponent:
- 0.5 (for the Weymouth equation)
- 0.5392 (for the Panhandle “A” equation)
- 0.51 (for the Panhandle “B” equation)
In these equations, the Z-Factor can is evaluated at the average pressure, :
Some investigators suggest that a more representative definition of average pressure, and hence a more accurate result, can be obtained with the following definition of average pressure:
When both the inlet pressure and the outlet pressure are known and the rate is the unknown, these equations (the Weymouth equation, the Panhandle “A” equation, and the Panhandle “B” equation) do not need an iteration for a solution. However, if the rate and one pressure are known and the other pressure is the unknown, then an iteration is still required. These equations can be used for tubing calculations or for calculations on long gas transmission pipelines. You will most likely see options for them if you use industry pipe flow or Nodal Analysis software. (Nodal Analysis is a well optimization technique where all components, or nodes, of the production system are modeled – the reservoir, skin, tubing, wellhead choke, flow line, and surface facilities – to identify any bottlenecks in the system for possible remediation or Debottlenecking.) For well modeling applications, Equation 6.17 through Equation 6.19 can be used to evaluate the pressure loss in the wells, in the Flow Lines (small ID pipe used to transport produced oil or gas from the wellhead to a gathering station, field separator, or other surface facility), and in gas transmission lines.
[9] Cullender, M.H., Smith, R.Y.: ''Practical Solution of Gas-Flow Equations for Wells and Pipelines with Large Temperature Gradients," Trans., AIME, 1956, vol. 207, p. 281.
6.3.4: Multi-Phase Flow
Well Modeling
Well Modeling is the process of developing models (supplying input) for actual wells and using these data in Well Modeling Software to perform the analyses required by the engineer. In all of our discussions to this point, we have assumed single-phase flow of either liquid or gas. Pressure loss calculations in multi-phase flow are much more complicated than those for single-phase flow. This is because in single-phase flow, the only frictional losses that occur in the system are at the fluid-pipe interface. In multi-phase flow, there is also the friction loss between the phases. As we have also seen in our discussion on flow regimes in tubing, there are multiple flow regimes that can occur in vertical, deviated, and horizontal wells and these can have a significant impact of energy and momentum transfer.
To quantify the pressure losses occurring in multi-phase flow calculations, we must consider the physics that are occurring in each flow regime. Typically, in the oil and gas industry, for multi-phase flow we evaluate the physics empirically. Table 6.05 lists the important physical data that have been observed to have a significant impact on the pressure drop in well tubing. These empirical physics are input into the well model with a Multi-Phase Flow Correlation.
There are many multi-phase flow correlations available and most pipe flow or nodal analysis software contains options for the most relevant correlations for crude oil and natural gas flow. The details of these multi-phase flow correlations are beyond the scope of this class, so I will briefly give a general description of them and then discuss the common correlations used in the oil and gas industry.
Well Model Data
As we have already discussed, the energy balance is a steady-state equation while our flow calculations are unsteady-state problems. When we use the energy balance equation to solve unsteady-state problems, we are solving a category of physical problems called a Series of Steady-States where the equation is derived for steady-state conditions, but we are solving it with time-dependent input data.
In Table 6.05 there are color coded entries: some of the data I have listed as Static Data which implies they do not change with time or location. Other data I have listed as Dynamic Data which implies that they may change with time, location, or both.
The entries in the green cells (Table 6.05 rows 1-6) are the data that make up a Well Model. These data are entered into the well modeling software and are treated as fixed data for some time period or some length of tubing. For example, I have already mentioned tapered tubing strings where the diameter of the tubing may change with position. When a well model is constructed, these design changes can be implemented as part of the segmented well model.
| Data or Property | Symbol | Description |
|---|---|---|
| Tubing/Pipe Diameter | Dynamic data but treated as static data | |
| Downhole well equipment | Pumps, chokes, etc. | Static data |
| True vertical depth, TVD | Vertical depth – depth in the true vertical direction | |
| Measured depth, MD | Measured depth – physical length of tubing | |
| Absolute or Relative Roughness | Dynamic data but treated as static data | |
| Efficiency | Dynamic data but treated as static data | |
| Liquid Hold-Up | Dynamic data: fraction of a representative elemental volume (REV) occupied by liquid (analogous to liquid saturation in the reservoir). | |
| Gas Hold-Up | Dynamic data: fraction of a representative elemental volume (REV) occupied by gas (analogous to gas saturation in the reservoir). | |
| Slip (or Slip Velocity) | Dynamic data (difference between velocities of two different phases). | |
| Gas-Liquid Ratio | Dynamic data: used as input to our pressure traverse or tubing performance calculation. | |
| Gas-Oil Ratio or | Dynamic data: used as input to our pressure traverse or tubing performance calculation. | |
| Watercut or | Dynamic data: fraction of the water rate in the total liquid rate. Used as input to our pressure traverse or tubing performance calculation. | |
| Water-Oil Ratio or | Dynamic data: ratio of the water water rate to the oil rate. Used as input to our pressure traverse or tubing performance calculation. | |
| Oil, Gas, and Water PVT Properties | Dynamic data: Pressure-Volume-Temperature description of all fluids. | |
| Well Head Pressure | Dynamic data: one of the primary knowns/unknowns of the problem. | |
| Bottom-Hole Pressure | Dynamic data: one of the primary knowns/unknowns of the problem:
|
|
| Production/Injection Rate | Dynamic data: one of the primary knowns/unknowns of the problem. |
Static data may also change due to a well intervention. For example, a production engineer may decide to perform a Tubing Change-Out Workover, where all or portions of the tubing string are removed from the well and replaced with new tubing (either the original size or a new size). When a new tubing string is used, or a new piece of downhole equipment is installed, this is considered a new well design, and a new model must be used.
I have listed some of the data in the table as “Dynamic data but treated as static data.” This is because some data that are typically assumed to be fixed with time may, in fact, change. For example, the efficiency, absolute roughness, and relative roughness may change as the tubing degrades over time due to erosion, corrosion, or wax/asphaltene/scale deposition. I have also included the tubing/pipe diameter in this category of data because severe Scale Deposition (deposition of minerals from the produced water) can be a significant issue with certain produced water compositions and can significantly reduce the effective diameter of the tubing. This is shown in Figure 6.10. This figure also illustrates why tubing change-out workovers may be performed.
I have also highlighted some entries in Table 6.05 with blue cells (rows 7-9.) These entries are dynamic data that typically are not of interest to most production engineers and are not entered explicitly into a well model. These data are entered implicitly into the model by the choice of the multi-phase flow correlation selected by the engineer. I will discuss these dynamic data and these multi-phase flow correlations in more detail later in this lesson.

The table entries highlighted with orange cells (Table 6.05 rows 10-14) are entries with dynamic data that are of interest to the production engineers and are explicitly input into the well model. In actuality, only a subset of these data is required because the rates, , , and , are sufficient to specify the problem. For example, the oil rate, , the gas-oil ratio, , and water-oil ratio, , are sufficient to specify total production. Likewise, the liquid rate, , the gas-liquid ratio, , and watercut, , are also sufficient to specify total production.
Finally, the table entries highlighted with yellow cells (Table 6.05 rows 15-17) are entries that are either specified or calculated by the well model. As I mentioned earlier, as production engineers, we are typically concerned with two types of problems, Pressure Traverse Calculations, where we specify the flow rate and calculate the pressure drop, and Tubing Performance Calculations, where we specify one pressure and the total rate and calculate the other pressure (typically the flow bottom-hole pressure, ).
6.3.4.1: Multi-Phase Flow Correlations
As we have discussed, multi-phase flow through tubing is typically performed using empirical, multi-phase flow correlations. These empirical correlations are developed on the observations made by the investigator in laboratory experiments, field measurements, or both. The differences in the correlations are based on many factors including:
- experimental technique
- tubing orientation
- vertical
- slanted
- horizontal
- tubing type
- smooth
- rough
- fluids used in the experiments
- air-water
- crude oil - natural gas
- pressure-temperature range used in the experiments
- tubing orientation
- flow regimes observed during the experiments and how they are incorporated into the correlations
- trade-off between the desired accuracy and the desired degree of mathematical simplicity or ease of application
In most cases, the multi-phase flow correlations are based on the flow regimes that we have already discussed. For use in a multi-phase flow correlation, these flow regimes are plotted as Flow Pattern Maps. Examples of the flow pattern maps are shown in Figure 6.11 (for vertical flow) and Figure 6.12 (for horizontal flow).

Where: and

Where:
and
The example flow regime maps shown in Figure 6.11 and Figure 6.12 illustrate two important points. The first point is how the flow regimes are incorporated into the flow correlations. The variables on the x-axis and y-axis are calculated, and that point on the map indicates the flow regime that is occurring in a well segment based on the investigator’s experimental or field results. For the flow regime identified on the flow pattern map, different mathematical expressions are used to quantify the Liquid Hold-Up, Gas Hold-Up, the slip velocity, and the friction factors within that particular flow regime. These dynamic data are the data that I identified in Table 6.05 with the blue cells. Once the dynamic data are calculated for a particular segment in a segmented well model, they are used in the energy balance equation to determine the pressure loss in that segment.
The second point illustrated by the example flow pattern maps is that the definitions of the x-axis and y-axis are different for each multi-phase flow correlation. This gets back to the empirical nature of the multi-phase flow correlations. Different investigators and different experimental/field procedures may result in different mathematical groups controlling the dynamics of the flow. The choice of these mathematical groups may also lie in the personal preference of the investigator.
For multi-phase flow, the fluid properties are typically calculated as mixture properties. These mixture properties are based on the Phase Hold-Up, and . Hold-Up is the local fraction of the pipe volume occupied by the phase. In multi-phase flow correlations, the hold-up is determined from the map based on the mathematical expressions related to the flow regime. Once the hold-up is determined, fluid properties can be determined for the flowing mixture by:
for viscosity, some investigators prefer to use a different definition of mixture viscosity:
As a practical point, a working production engineer typically is not expected to know the details of the multi-phase flow correlation used in a well model. There is no universal rule for selecting the proper correlation for use for a particular well, group of wells, or wells in a field. The production engineer simply performs Flow Tests on his/her wells to see the actual pressure drops at the current reservoir conditions (orange and yellow table entries in Table 6.05) for known production rates and selects the multi-phase flow correlation that best matches the flow test results. Many software packages allow for the use of different multi-phase flow correlations for different segments of a segmented well model for one well. In other words, one well may use a different multi-phase flow correlation along different segments of the well.
Description of Multi-Phase Flow Correlations in Use in the Oil and Gas Industry
There are many multi-phase correlations used in the oil and gas industry. It is beyond the scope of this course to discuss all of the correlations in use today. Table 6.06 lists many of these correlations used in industry software along with notes describing their preferred applications.
| Single-Phase Flow |
Gas | Darcy-Weisbach | Theoretical Energy Balance. Uses a general friction factor. Requires an iteritive solution for copressible fluids. Can be used for wells (verticle, inclined, or horizontal), flow lines, or transmission lines. |
| Weymouth | Empiricla Energy Balance. Uses an equation specific friction factor. A non-iterative solutionis possible if inlet and outlet ressures are specified. An iterative solution is required otherwise. Can be used for wells, flow lines, or transmission lines. | ||
| Panhandle "A" | Empiricla Energy Balance. Uses an equation specific friction factor. A non-iterative solutionis possible if inlet and outlet ressures are specified. An iterative solution is required otherwise. Can be used for wells, flow lines, or transmission lines. | ||
| Panhandle "B" | Empiricla Energy Balance. Uses an equation specific friction factor. A non-iterative solutionis possible if inlet and outlet ressures are specified. An iterative solution is required otherwise. Can be used for wells, flow lines, or transmission lines. | ||
| Cullender and Smith | Empirical Energy Balance. Uses an equationspecific friction factor. Requires an iterative solution. | ||
| Liquid | Darcy-Weisbach | Theoretical Energy Balance. Uses a general friction factor. Requires an iterative solution for slightly compressible liquids. Can be used for wells (vertical, inclined, or horizontal), flow lines, or transmission lines. | |
| Hazen-Williams | Empirical. The friction factor is replaced with material specific constant. Requires an iterative solution for slightly compressible liquids. Used for water disposal, water source, water injection, or light hydrocarbon wells (possible use in condensate reservoirs). | ||
| Multi-Phase Flow |
Vertical Flow |
Fancher and Brown (no slip and no flow pattern map) |
The no slip assumption and no pattern map imply that the correlation is not generally applicable.The no slip assumption is only applicable in flow regimes where liquid and gas velocities are the same. |
|---|---|---|---|
| Hagedorn and Brown | Developed from experiments on 1,500 ft experimental well using 1 inch to 4 inch tubing. Experiments included thre-phase flow. One of the most commonly used multi-phase flow correlations for vertical or near vertical wells. | ||
| Beggs and Brill (no slip) |
The no slip assumption is only applicable in flow regimes where liquid and gas velocities are the same. One of the few multi-phase flow corrections capable of modeling vertical, inclined, or horizontal flow. Assumes smooth pipe. | ||
| Beggs and Brill (with Darcy-Weisbach friction factor) |
The no slip assumption is only applicable in flow regimes where liquid and gas velocities are the same. One of the few multi-phase flow corrections capable of modeling vertical, inclined, or horizontal flow. Pipe is allowed to include roughness. | ||
| Orkiszewski | Took existing correlations and compared them to field results. Selected the best correlations for different regimes and developed a single correlation. This is apopular multi-phase flow correlation, but may exhibit discontinuities when crossing regime boundaries. | ||
| Gray | Developed for gas condensate reservoirs (most accurate for these reservoirs). Uses non-compositional approach. It is based on the observation that hold-up is not as great in condensate wells as in oil wells. Roughness is ignored, but uses an efficiency instead. | ||
| Gray (with Darcy-Weiabach friction factor) |
Developed for gas condensate reservoirs (most accurate for these reservoirs). Similar to the standard Gray correlation, but roughness is incorporated through the Moody Diagram. | ||
| Duns and Ros | Uses combined experimental and field measurements. The first multi-phase flow correlation to use flow pattern mapping. A popular multi-phase flow correlation. | ||
| Horizontal Flow |
Eaton-Flanigan | This correlation is a hybrid correlation of the Eaton hold-up and friction loss correlations and the Flanigan inclined pipe correlation | |
| Eaton-Dunkler-Flanigan | This correlation is another hybrid correlation of the Eaton hold-up correlation, the Dukler friction correlation, and the Flanigan inclined pipe correlation. | ||
| Beggs and Brill (no slip) |
The no slip assumption is only applicable in flow regimes where liquid and gas velocities are the same. One of the few multi-phase flow correlations capable of modeling vertical, inclined, or horizontal flow. Assumes smooth pipe. | ||
| Beggs and Brill (with Darcy-Weisbach friction factor) |
The no slip assumption is only applicable in flow regimes where liquid and gas velocities are the same. One of the few multi-phase flow correlations capable of modeling vertical, inclined, or horizontal flow. Pipe is allowed to include roughness. |
6.3.4.2: Multi-Phase Flow Calculations
The analyses used for multi-phase flow are identical to those used for single-phase flow: pressure traverse calculations and tubing performance calculations. Figure 6.13 shows typical multi-phase pressure traverse plots using the Hagedorn and Brown Correlation. As seen in the legends of these plots, this figure indicates that the pressure drop is dependent on all of the properties listed in Table 6.05.
The difference in the pressure traverse curves shown in Figure 6.13, is the Watercut (fraction of water) in the produced stream: 0.0 for the family of curves on the left and 0.5 for the family of curves on the right. In these pressure traverse curves, the Static Properties (properties that are assumed to be constant over time) are the tubing I.D. the tubing lengths (TVD and MD), the oil API gravity, the gas specific gravity, and the water specific gravity; while the Dynamic Properties (properties that normally vary over time) are the wellhead pressure, the watercut , the gas/liquid ratio (GLR), and the production (liquid) rate. Other dynamic properties that are changing in the calculations include the flow regime, the hold-up, the local fluid (and mixture) properties, and friction factor.

Figure 6.14 shows typical multi-phase tubing performance curves using the Hagedorn and Brown correlation. This figure shows a single, 10,000 ft tubing string with three different watercut values, 0.0, 0.5, and 0.9. The reason that the curve with the highest watercut (blue curve) has the highest flowing bottom-hole pressures, , is because water has a higher density than the oil which results in a heaver fluid column in the well. In the case of Figure 6.14, the 35º API crude oil has a specific gravity of 0.85, while the water has a specific gravity of 1.0.

6.4: Key Learnings
- Three common well orientations for crude oil and natural gas production are vertical wells, deviated (or slanted) wells, and horizontal wells. These wells have different applications in field development, but all can be modeled with contemporary well modeling software.
- Tubing hydraulics during crude oil and natural gas production is a very complex physical problem, particularly for multi-phase flow. These parameters that impact tubing hydraulics include:
- the well design: well orientation and tubing size
- the well condition: absolute and relative roughness
- the production rate: dependent on reservoir inflow performance
- number and types of flowing phases: this will change based on:
- the location of the fluids in the well (with respect to the local bubble-point pressure)
- pressure depletion in the reservoir
- the fluid properties: density, viscosity, etc.
- the local flow regimes in the segment tubing:
- laminar or turbulent
- multi-phase flow regimes illustrated in Table 6.01 and Table 6.02
- Fluids flowing through tubing do not flow as homogeneous fluids but may go through many flow regimes or flow patterns:
- for vertical flow:
- single-phase flow
- bubble flow
- slug flow
- churn flow
- annular flow
- mist flow
- for horizontal flow:
- single-phase flow
- bubble flow
- plug flow
- stratified flow
- wavy flow
- slug flow
- annular flow
- spray flow
- for vertical flow:
- The well does not necessarily need to pass through all of these flow regimes. The flow patterns can be quantified for numerical calculations with flow pattern maps. Flow regime maps are empirically based maps that indicate the flow regime at know pipe/tubing conditions (x-axis and y-axis on the flow pattern map).
- The fundamental relationship for tubing hydraulics is the energy equation developed by Bernoulli.
- The energy balance equation that was specifically adapted from Bernoulli’s equation for pipe/tubing flow is the Darcy-Weisbach Equation. The Darcy-Weisbach Equation can be used for all single-phase flow conditions. Friction losses in well tubing are calculated with Darcy-Weisbach Friction Factor. The Darcy-Weisbach Friction Factor is plotted in the Moody Diagram as a function of the Reynolds Number and the relative roughness of the pipe/tubing.
- Other empirical single- phase flow correlations can be used for tubing hydraulics:
- liquids: the Hazen-Williams Equation for water and light hydrocarbons
- gases: the Weymouth equation, the Panhandle “A” equation, and the Panhandle “B” equation
- There are two main types of tubing hydraulics calculations used by Production Engineers: Pressure Traverse Calculations and Tubing Performance Calculations. Pressure traverse calculations are based on a known flow rate, , and an unknown pressure drop, . Tubing performance calculations are based on a known flow rate, , a known wellhead pressure, , and an unknown flowing bottom-hole pressure, .
- For multi-phase flow, the flow problem is too complex to solve theoretically, and empirical flow correlations based on the flow patterns maps are used. The flow pattern maps have empirical correlations for hold-up, slip, and friction for the different flow regimes observed in laboratory and field experiments. These correlations are used in the energy balance equation to perform tubing hydraulics calculations. The multi-phase correlations currently in use in the oil and gas industry include:
- Verical flow:
- Fancher and Brown
- Hagedorn and Brown
- Beggs and Brill
- Orkiszewski
- Gray
- Duns and Ros
- Horizontal and deviated flow:
- Eaton-Flanigan
- Eaton-Dukler-Flanigan
- Beggs and Brill
- Verical flow:
6.5: Summary and Final Tasks
Summary
In this lesson, we discussed a very important task performed by production engineers working on crude oil and natural gas production wells. This task is to calculate the pressure drop in well tubing. As we will see, this is a very powerful tool for helping production engineers design and optimize production and injection wells. In addition to aiding in the initial well design, these analyses help in decisions on improving well performance, such as, adding artificial lift (gas lift or pump) to the well, stimulating the well (hydraulic fracture or acidation), and other workovers and well interventions.
In this lesson, we discussed the basics of tubing hydraulics related to oil and gas production. The well hydraulics are governed by an energy balance that relates the pressure, velocity, and elevation of a flowing fluid to its potential energy and frictional losses. The resulting equation, the Darcy-Weisbach Equation, related the rate flowing through the pipe/tubing to the pressure drop in the tubing.
For single-phase flow, the flow problem can be solved with theoretical considerations, while for multi-phase flow empirical correlations are used. These multi-phase flow correlations are based on flow pattern maps which enable different mathematical descriptions of dynamic two-phase data (such as, hold-up, slip velocity, and frictional losses) in different flow regimes. For selection of the appropriate correlation, production engineers reply on flow tests to assess the accuracy of the different flow correlations and to calibrate these correlations to their wells.
Final Tasks
Complete all of the Lesson 6 tasks!
You have reached the end of Lesson 6! Double-check the to-do list on the Lesson 6 Overview page [73] to make sure you have completed all of the activities listed there before you begin Lesson 7.
Lesson 7: Production Engineering: Well Intervention
7.0: Lesson Overview
In this lesson, we will discuss the design of oil and gas wells. As we have discussed in earlier lessons, Production Engineers are concerned with optimizing production from a given well. To achieve this, production engineers are the key architects of well design. In this lesson, we will discuss several important aspects of well design considered by the production engineer. These well design aspects include:
- well orientation
- completion design
- well stimulation
- artificial lift
We will see that two of the main tools used in the well design have already been discussed in this course:
- The Inflow Performance Relationships, IPR (Lesson 4 and Lesson 5)
- The Tubing Performance Curves, TPC (Lesson 6)
While the initial well design is the design that the well will use for the majority of its productive life, it may change over the life of the reservoir. Routine modifications to the well in response to changing well or reservoir conditions are referred to as Well Interventions or Workovers. Modifications to the well design may also be proactive, such a well recompletion, in advance of a change in the reservoir management strategy for the reservoir or field.
Many of the design aspects of the well, such as well stimulation or artificial lift, can be included in the initial well design or may be applied later in the life of the well as part of a workover.
Learning Objectives
By the end of this lesson, you should be able to:
- list and understand the overriding well considerations of well design;
- describe several of the more common well objectives of a well design;
- discuss important well components in well design and how production engineers use the components to address the overriding well considerations and well objectives;
- list and explain the different well orientations used in the oil and gas industry and discuss some of the common applications of these well orientations;
- discuss the need for sand control in wells and what components of the well are used to address sand control;
- list and discuss the mechanisms of unwanted fluid production from a well;
- discuss the need for zonal isolation in wells and what components of the well are used to address zonal isolation;
- explain the role of the well completion in a well;
- list and discuss common pieces of well equipment and their uses in a well completion;
- describe the role of production tubing in a well;
- discuss how to determine the appropriate size of the production tubing for a well;
- explain the significance of the Inflow Performance Relationship and Tubing Performance Curve in well design;
- explain the need and role of well stimulation in well design; and
- explain the need and role of artificial lift in well design.
Lesson 7 Checklist
| To Read | Read the Lesson 7 online material | Click the Introduction link below to continue reading the Lesson 7 material |
|---|---|---|
| To Do | Lesson 7 Quiz | Take the Lesson 7 Quiz in Canvas |
Please refer to the Calendar in Canvas for specific time frames and due dates.
Questions?
If you have questions, please feel free to post them to the Course Q&A Discussion Board in Canvas. While you are there, feel free to post your own responses if you, too, are able to help a classmate.
7.1: Introduction
In this lesson, we will discuss several tasks performed by production engineers. In particular, we will discuss well designs, artificial lift, well stimulation, and well interventions. Most fields and reservoirs are developed by Asset Teams composed of Development Geologists, Drilling Engineers, Production Engineers, and Reservoir Engineers. The responsibilities of each team member often overlap those from other disciplines; however, the tasks listed above are predominantly carried out by the production engineer.
To illustrate the overlap, the overall field development strategy is developed by the team based on their own knowledge and skills. Based on the anticipate geology, the development geologist and production engineer will design the well. This well design includes the completion design and the tubing size (the completion is the portion of the well that connects the well tubing to the reservoir). As we will see, the completion design is heavily influenced by the geology of the reservoir. The implementation of the completion design is performed by the drilling engineer and the production engineer.
7.2: Well Design
The overriding well design considerations are:
- well costs;
- tubing and completion longevity;
- well simplicity and reliability;
- ability to achieve all (or most) of the objectives of the well.
As in all industries, the oil and gas industry is focused on keeping expenses as low as possible. This is true for well designs which are planned to be as low cost as possible while retaining the ability to keep the well safe for people and the environment. One important aspect of low costs is the longevity, or life span, of the well and completion. While changing tubulars and well completions is a common practice in the oil and gas industry; multiple, frequent changes goes against the concept of low costs.
Two aspects of the well design that lead to a longer life span are the durability of the equipment and the flexibility of the well to handle changing reservoir conditions. As we have seen in earlier lessons, these changing reservoir conditions include lower pressures caused by fluid production, lower production rates caused by the lower pressures, and changing Gas-Oil Ratios (GOR) and Watercuts () over the life of the reservoir. Flexibility in well design includes the ability of the original design to handle all of the anticipated reservoir changes or, if this is not possible, designing the original completion to be able to be modified to handle these changes at the lowest possible costs.
Finally, the well must be able achieve the objectives of the well. There are many objectives other than oil or gas production that can be designed into the well. These include:
- sand control for reservoirs made up of unconsolidated reservoir rock or rock susceptible to Fines Movement (movement of fine-grained materials within the rock);
- zonal isolation for reservoirs with multiple zones (to allow each individual zone to be shut in, if required);
- well stimulation for reservoirs with low permeability or susceptible to well damage; and
- artificial lift for low rate wells.
7.3: Well Design Considerations
The main well consideration is the anticipated production rate from the reservoir. As we saw in the previous lesson, the pressure drop for a given tubing size is directly related to the production rate (or rates for multi-phase flow). For a naturally flowing well, the reservoir pressure must be great enough to lift the reservoir fluids up the well and deliver these fluids to the surface facilities. Therefore, the producing rate needs to be considered in the sizing of the tubing.
For the same reasons, the current and future reservoir pressures must also be considered in the well design. It is this pressure that drives the fluids to the production facilities. If the pressure has dropped too low due to fluid production, then artificial lift (gas lift or pumps) may be required.
The geology of the reservoir is also of vital importance in the well design. As we will see, reservoirs consisting of a single zone (or reservoir layer) may have one type of completion, while reservoirs comprised of multiple zones may require more complex completions. Typically, we would like to be able to isolate individual zones (or groups of zones) at some future point in time if required. This would occur if the reservoir conditions in some zones change at a different rate than in other zones. For example, if a well is originally producing at a low watercut, , and at some future date, one layer begins to produce water at a higher watercut than the other reservoir layers, then, we would want to be able to isolate this high watercut zone (to shut it in), while continuing to produce from the low watercut zones. We will see that some well completions will allow us to provide this ability for zonal isolation, while others will not.
In addition, as mentioned earlier, if the reservoir rock is comprised of unconsolidated rock or rock susceptible to fines migration, then we will need to design wells and completions that allow for sand control. If sand or fines enter the well, they will settle at the bottom of the well and may eventually result in Sand Fill: sand or rock material accumulating in the well and covering some or all of the well perforations.
Also, if the reservoir rock is low permeability, then we may need to consider stimulating the well in our original completion design. This how we produce gas in unconventional gas wells, such as Marcellus Shale wells in Western Pennsylvania. Figure 7.01 illustrates a typical well completion for a Marcellus Shale well.

In this completion design, a long horizontal well is stimulated with multiple hydraulic fractures. The need for this type of completion is because of the ultra-low permeabilities in shale reservoirs. Shale permeabilities, including the Marcellus Shale, range from nano-Darcies (10-9 Darcies) to micro-Darcies (10-6 Darcies). These orders of magnitude are in contrast to the milli-Darcies, md, (10-3 Darcies) that we typically deal with in the oil and gas industry. The reason that the Marcellus Shale has opened up in the last two decades is because of completions like that shown in Figure 7.01 and the technologies behind these completions.
In addition, deep wells will inevitably encounter high pressures and temperatures and often encounter high concentrations of Acid (Corrosive) Gases, hydrogen-sulfide, H2S, and carbon-dioxide, CO2. In addition to being a very corrosive gas, H2S, is highly toxic. The high pressures and temperatures require all downhole equipment be certified for those conditions. All well tubulars in highly corrosive environments require special CRA (Corrosive Resistant Alloys) steel.
In earlier lessons, we discussed the drive mechanisms in oil reservoirs. These drive mechanisms may have some significance in the types of well completions used in the reservoir. The natural drive mechanisms for oil reservoirs encountered during Primary Production (the first stage of oil production) are:
- rock and fluid expansion
- solution gas drive
- gas cap drive
- gravity drainage
- natural aquifer drive (or water encroachment)
From this list, two of the drive mechanisms, solution gas drive and gas cap drive, are drive mechanisms that are due to the presence of a free gas phase. If this free gas results in high producing GORs, then the well completion must be capable of handling this gas or capable of isolating the reservoir zones containing the free gas. Likewise, the natural aquifer drive may result in mobile water in the reservoir and excessive water production with high watercuts. Again, the well completion must be designed to be able to isolate this water production.
During Secondary Production (a second stage of oil production), we may inject gas or water into the reservoir to displace oil towards the production wells. In these cases, we will need totally different well designs for our injection wells than we would use for our production wells. In addition, since we are adding these external fluids into the reservoir, we must plan our production wells to eventually produce some of these fluids. For example, if we are injecting water, even if our original well and completion design allows for zonal isolation, we will eventually start producing this water. As we saw in Lesson 6, the presence of water in the produced fluids will result in a heavier well stream, and we may need to consider artificial lift (gas lift or pump) for our production wells. As a second example, if we inject steam to improve recovery of high viscosity oils, then all of our downhole equipment must be certified for production at these elevated reservoir temperatures.
As we can see, there are many possible situations that can be encountered by a single well and infinitely more combinations of these situations. Therefore, there is no “cookbook” for well design. The best advice that I can give is to let the nature of the problem dictate the nature of solution. We can go over several common situations and example completion and well designs used in these situations.
In this lesson, we will discuss the following aspects of well design:
- well orientation
- completion design
- tubing size
- artificial lift
- well stimulation
7.4: Well Orientation
We will start our discussion on well design by discussing the well orientation. In past lessons, we discussed three of the more common designs: vertical, deviated, and horizontal. These will be the well orientations that we will focus on. There are shown in Figure 7.02.

There are many other well orientations and configurations that are possible. One broad category of these more complex wells is the category of Multi-Lateral Wells. A small subset of possible multi-lateral wells is shown in Figure 7.03. Using the naming convention in Figure 7.03, a horizontal well would be called a Single-Lateral Well. The term Lateral refers to the number of horizontal branches emanating from a single vertical well section.
Historically, the most common on-shore wells have been vertical wells. This is because of their simplicity and economics. It turns out that straight vertical wells are the most economic wells that can be drilled. Rigs are contracted on a daily basis, and the fastest way to drill a well is with a vertical well (This is the shortest distance to the target because the measured depth, MD (the length that is actually drilled), is equal to the true vertical depth, TVD – see Figure 7.02.).
For offshore production wells, the most common wells tend to be deviated wells. In offshore drilling, we are normally dealing with a rig at one to three fixed drilling centers, the Production Platforms (there are other drilling centers). In these situations, the drilling rig is at a fixed position, and the vertical section of the well is drilled. The bottom-hole well target for the well is the desired location where we want to produce. In order to reach this location, we need to deviate from the vertical and drill towards the bottom-hole target. The point where we deviate from the vertical is referred to as the Kickoff Point. Deviated wells are typically more expensive than vertical wells because the measured depth is greater than the true vertical depth, so the drilled footage is greater. In addition, all casing and tubing will need to be the measured depth of the well, so costs such as casing, tubing, and cement, will be greater for a deviated well.
On-shore wells are now commonly drilled from Well Pads (temporary, compact drilling sites that are prepared specifically for drilling using local materials – for example, gravel and wood – and then removed once drilling operations are completed). Pad drilling is a relatively recent innovation and, as it turns out, deviated wells drilled from Multi-Well Pads can leave a smaller environmental footprint than vertical wells drilled from Single-Well Pads. Therefore, there is an environmental incentive for drilling deviated wells from multi-well pads. There may not be an economic incentive for multi-well pad drilling as any synergies and cost reductions captured at the surface must compensate any cost increases associated with the deviated well.

Deviated wells drilled from multi-well pads are similar to deviated wells drilled from an offshore drilling center. Wells with a common surface location are drilled to different bottom-hole targets identified by geologists and reservoir engineers.
There are many uses for deviated and horizontal (or single-lateral) wells. These include to:
- avoid well surface locations that:
- are environmentally sensitive;
- are logistically difficult (heavily forested, no suitable access roads or infrastructure, heavily populated regions, etc.);
- drill an offshore bottom-hole target from an onshore surface location;
- produce from thin formations;
- produce from low permeability formations
- produce a thin oil column in a gas or gas condensate reservoir;
- maximize the contact area of the well and reservoir;
- reduce pressure drop near the well:
- minimize production of unwanted fluids in Coning situations (I will discuss coning later in this lesson);
- minimize sand production;
- intercept natural fractures in naturally fractured reservoirs;
- assist in steam drive production of heavy oils.
If the bottom-hole target location of a well is positioned directly below a non-desirable surface location from environmental, economic, logistics, or safety perspectives, then vertical wells may not be the best option if the target location can be reached with a deviated or horizontal well. If a more desirable surface location can be found within the Drilling Radius for that bottom-hole location, then deviated or horizontal wells should be considered.
From a production perspective, horizontal wells are often more desirable for thin bottom-hole targets (reservoirs or oil columns). While vertical well lengths are limited to the reservoir thickness, that restriction does not apply to horizontal wells (see Figure 7.02). The longer the well length, the more contact area is exposed to the well. This increases the inflow performance of the well and results in higher production rates at comparable or lower drawdowns. One advantage of these lower drawdown pressures is that this helps reduce production of unwanted fluids in coning situations. I will discuss this later in this lesson.
Finally, for specialized situations, such as Naturally Fractured Reservoirs or Steam Flooding, horizontal wells also have applications.
7.5: Well Completion Design
The well completion is the lowermost portion of the well, comprised of tubulars and downhole equipment, that enables the safe and effective production from an oil or gas well. The objectives of the completion are to:
- connect the reservoir to the production tubing;
- provide a conduit for well stimulation fluids;
- protect the well from sand/fines production;
- isolate productive zones from non-producing zones;
- isolate oil producing zones from high GOR (gas-oil ratio) and high watercut zones in oil reservoirs;
- isolate gas producing zones from high GLR (gas-liquid ratio) zone in gas reservoirs;
- provide a means to measure changes in reservoir conditions (pressure, saturation, rate) by well tests, cased-hole logs, and production logs.
Before we can discuss well completions, we will need to discuss sources of production problems. The problems that we will further discuss in this lesson are production of sand and production of unwanted fluids (gas and water from oil reservoirs and water from gas reservoirs).
We have already discussed that in reservoirs made of unconsolidated reservoir rock or in reservoirs with fine rock materials, there is a possibility that the rock material and debris may be dragged along with the produced fluids and enter the well. As I mentioned earlier, this this is referred to as Fines Movement or Fines Migration. Once inside the well, if the velocity of the fluids going up the well is less than the settling velocity of the sand, then Sand Fill will occur in the well. Sand fill is the settling of sand and debris originating from the reservoir which entered the well and settled on the bottom of the well. This has the potential to cover some or all of the perforations in a perforated well. This is illustrated in Figure 7.04.
In this figure, sand fill has covered approximately half of the perforations and is severely restricting flow from the reservoir. The ineffective perforations and the restricted flow shown in Figure 7.04 result in well damage and is quantified as a Skin Factor in our Inflow Performance calculations.
If the velocities of the fluids are greater than the settling velocity of the sand, then produced sand will continue upward and cause erosion of the tubing and possible damage to any down-hole equipment (down-hole pumps, pressure gauges, etc.). The detection and avoidance of sand production is referred to as Sand Control.
Another potential problem in hydrocarbon production is the production of unwanted reservoirs fluids. As petroleum engineers, we are attempting maximize the recovery and profit of a well for our employers and key stake holders. To achieve this, we are interested in producing the most valuable resource from the well. In the case of oil reservoirs, this means the production of oil. While natural gas is also produced from oil reservoirs and has a sales value, crude oil has historically commanded a higher commodities price than natural gas. Consequently, production engineers working on oil reservoirs will focus their attention on oil production and, in fact, in many cases attempt to shut off gas production.

As we have seen in earlier lessons, free gas in the reservoir (either liberated solution gas or initial free gas) expands and displaces oil to the production wells. This expanding gas is the cause of two of the oil drive mechanisms: solution gas drive (liberated solution gas) and gas cap drive (initial free gas). From the reservoir side, the production of the free gas results in removing a source of reservoir energy available to oil production.
From the tubing side, the production of free gas can have different impacts based on the production rate of the free gas, At low rates, the addition of gas will lighten the well column and aid oil production. On the other hand, excessive gas rates may result in higher frictional losses and, in turn, result in a high back-pressure across the perforations. From our discussions on inflow performance and Darcy’s Law, we saw that the lower that we can keep the flowing well pressure, the greater the drawdown will be and the higher the oil production rate will be. It is the role of the production engineer to assess the impact of gas production (both from the reservoir side and the tubing side) to determine if/when gas shut-off is required.
For both oil reservoirs and gas reservoirs, the production of water is always avoided if economically warranted. Since water is a heaver fluid than either gas or oil, water production results in a heavier well column and a larger back-pressure across the perforations. In addition, depending on the produced water chemistry, it may need to be treated to remove any heavy metals and disposed of. Water treatment and disposal require additional costs which reduce the economics of the well.
The detection, avoidance, treatment, and disposal of water is referred to as Water Control. The best method of water control is to shut off water in the reservoir. There are three common causes of production of unwanted fluid production. These are:
- lateral fluid movement from a gas cap or aquifer,
- lateral fluid movement from gas or water injection, and
- gas and water production from coning.
These mechanisms are shown in Figure 7.05 in the context of water production. In Figure 7.05 (A), water is being pulled laterally from the aquifer by the production from the well. The movement of water from the aquifer to the well is, in large part, governed by the permeability of the different reservoir layers with the water moving faster in the reservoir units with the highest permeability. In Figure 7.05 (B), water is being injected into the reservoir. The objective of this secondary waterflood is to displace oil to the production well with the injected water. At some point, the injected water Breaks Through to the production well resulting in increased producing watercuts. Finally, in Figure 7.05 (C), water is being pulled upward from a underlying or Bottom Water Aquifer. The production of water in this manner is referred to as water coning.

(A) Production Well with Lateral, Edge-Water Production.
(B) Production Well with Lateral, Injected-Water Production.
(C) Production Well with Bottom-Water Coning Production.
Each of these water producing mechanisms has a direct analog with a gas production mechanism. These gas production mechanisms are shown in Figure 7.06. The avoidance of production of sand and unwanted fluids are two major design criteria for well completions.
There are many types of completions, however, we will focus on the following:
- an Open-Hole or Bare Foot completion
- a Screen or Liner completion
- Slotted Liner completion
- Screen completion
- Gravel pack completion
- Cased and Perforated completion
7.5.1: Open Hole and Barefoot Completion
The least complex and least costly well completion is a Barefoot, Open-Hole completion. An open-hole completion is a completion that does not have any casing or tubulars cemented across the reservoir section, while a barefoot completion has no tubulars, casing or tubing, across the reservoir section (a barefoot completion is a subset of an open-hole completion). Two examples of barefoot, open-hole completions are shown in Figure 7.07, one without tubing and one with tubing.

(A) Production Well with Lateral Gas Production from the Gas Cap.
(B) Production Well with Lateral Gas Production from the Injection Well.
(C) Production Well with Gas Coning from the Gas Cap.
As with all decisions on completion design, there are advantages, disadvantages, and trade-offs associated with each decision regarding the open-hole, barefoot completions.
The advantages of a barefoot, open-hole completion include:
- they are the least expensive completion technique;
- they are adaptable to special drilling techniques that minimize reservoir damage (wells can be drilled to the top of the reservoir, casing set and cemented in place, and drilling/completion fluids changed to less damaging fluids for drilling through the reservoir);
- no perforating expenses;
- no issues with open-hole logging (time-lapse open-hole logs can be run for improved reservoir characterization and surveillance);
- large wellbore radius, , across the reservoir (From Lesson 4 and Lesson 5, we saw that a large wellbore radius improves Productivity Index and Inflow Performance – Table 7.01 and Table 7.02 have been reproduced to illustrate this point and to aid in later discussions);
- large diameter conduit to surface which results in lower pressure losses in high production rate wells (in Lesson 6, we saw that the pressure losses were significantly impacted by the the inner diameter of the conduit to the flow);
- the well can be easily deepened if desired;
- the completion can be modified at a later date with an inner casing string or liner if desired.
The disadvantages of a barefoot, open-hole completion include:
- as illustrated, sand production cannot be permanently controlled without a Major Rig Workover, MRWO (an expensive well intervention requiring a drilling rig and hoist). Temporary sand control can be performed with multiple bailer/clean-out well interventions (less expensive Slickline Workover). We will discuss Major Rig Workovers, Coiled Tubing Workovers, Wireline Workovers, and Slickline Workovers later in this lesson;
- as illustrated, excessive gas or water production cannot be easily controlled;
- selective well stimulation (acidizing or hydraulic fracturing of specific depth(s) in the reservoir) more difficult than with Cased and Perforated Completions;
- while the large diameter conduit for fluids flowing to the surface has the advantage of lower pressure losses, it has the disadvantage of lower velocity for the same volumetric rate. If the velocity of multiphase flow is too low, then the heavier fluids may segregate toward the bottom of the well causing a segregated water phase across the reservoir.


From the lists of advantages and disadvantages for barefoot, open-hole completions, we can see that these well completions would typically target reservoirs locations with limited chance of production of sand or unwanted fluids. These completion designs also illustrate that a field-wide well completion to be used on each and every well may not be desirable. For example, production wells close to a source of gas or water (see Figure 7.05 and Figure 7.06) may not be good candidates for the barefoot open-hole completions shown in Figure 7.07, while wells in the same reservoir down-dip from the gas cap or up-dip from the aquifer may be suitable candidates for these completions. In terms of sand control, the well completions shown in Figure 7.07 normally target hard, consolidated reservoir rocks.
There are several features of the well completions shown in Figure 7.07 that require further discussion. One common feature to these well completions is that there are no tubulars (casing or tubing) across the sandface. By definition, this is what makes these two completions barefoot completions. A second common feature to these completions is that casing has been set at the top of the reservoir. There are several reasons for running and setting this casing. These include:
- preventing reservoir fluids from entering porous and permeable formations above the reservoir;
- preventing heavier fluids from porous and permeable formations above the reservoir from entering the reservoir;
- preventing rock material and drilling debris from formations above the reservoir from entering the wellbore and settling across the reservoir sandface;
- preventing catastrophic wellbore collapse and loss of the well.
As seen in Figure 7.07, we can run a barefoot completion with or without a tubing string. Again, there are advantages and disadvantages to running a tubing string.
The advantages of running a tubing string include:
- the tubing permits for easy Circulation of fluids (corrosion inhibitors, scale inhibitors, solvents, Workover Fluids, or Kill Fluids) down the tubing and up the annulus (or Reverse Circulating fluids down the annulus and up the tubing). By running a tubing string without a production packer, we are setting up a three-dimensional U-Tube for these circulation process. Note, there are ways to circulate fluids with the temporary installation of Coiled Tubing (spooled tubing capable of being run into the well with the use of a drilling rig).
- provides multiple flow paths for artificial lift systems.
- protects the casing from erosion, corrosion, abrasion, or excess pressures.
- provides a means for monitoring bottom-hole pressures.
The disadvantages of running the tubing string in the completion in Figure 7.07 (B) are:
- the cost of the tubing;
- the rig time required to run the tubing:
- costs involved in paying the Day Rate for the rig;
- deferred production and revenue from the well.
Even the decision to run or not to run a Production Packer has advantages, disadvantages, trade-offs, and costs associated with it. A packer is device that is used to provide annular isolation for the well (prevent fluid flow through the annular space between the tubing and casing) and to anchor (secure) the tubing string to the production casing.
The advantages of including the production packer in the completion are:
- most common means of providing zonal control (isolation of reservoir layers) used in the industry
- isolates casing leaks or poor cement jobs in the well:
- protects the well from unwanted fluids entering the well;
- protects the subsurface environment from produced fluids exiting the well;
- protects the casing from excess pressure and corrosive fluids;
- protects the tubing from tubing leaks (Without a packer, the annular space between the tubing and casing will be filled with a static gas column while the tubing will be with a flowing liquid. The pressure differential caused by this pressure gradient disparity is conducive to tubing leaks. With a packer, the annular space is filled with a static fluid while the tubing is filled with a flowing fluid. This reduced pressure differential helps to prevent tubing leaks.)
- well safety (in conjunction with sub-surface safety valves)
- supports some of the weight of the tubing string
- some artificial lift systems
Many of these objectives, advantages, and disadvantages will become more clear later in the lesson when we discuss Zonal Isolation.
The disadvantage of running a Production packer are:
- additional cost (packer costs);
- difficulty in Recompleting the Well:
- Retrievable Packers can be easily unseated and removed; however, are much more expensive for the same functionality and less reliable than a permanent packer;
- Permanent Packers are extremely difficult to remove from a well once seated. To remove a permanent packer, the tubing above the packer must be removed (a standard operating procedure in the field), but the permanent packer must be milled out with a drilling rig and special milling bit.
Figure 7.08 is a schematic diagram of a simple, retrievable packer. I am supplying this Petrowiki link in the text (as well as in the reference) because the article contains a lot of good information on well completions and packers. While I was at it, I also provided the link to a Wikipedia article on well completions. The Wikipedia article has a good glossary of terms for much of the equipment that I will be discussing in the remainder of this lesson (and some terms that I will not be discussing). The links to these two articles are:
- PetroWiki Article [1]: Packers [74]
- Wikipedia Article: Completion (Oil and Gas Wells) [75]

Use your mouse wheel to zoom in and out, left mouse button to rotate, and right mouse button to move the model.
In this schematic, the threads at the top and the bottom of the packer are used to couple it to the tubing string. The packing element in the schematic is the element that creates the seal in the annulus. There are many ways that a packer can be actuated. These include:
- mechanical actuation (applying weight from the tubing string and rotating it with the rig). This is the actuation method used in the schematic diagram. Weight from the tubing string causes the sealing element to compress outward forming the seal;
- pressure actuation (inflating the sealing element with pressurized drilling, completion, or work over fluid);
- electrically actuated (inflating the sealing element with an electrically controlled pump – both pump and packer are run at the end of wire line. This method of actuation is typically used for tubing retrievable packer.)
The two links that I supplied provide additional information on the design aspects of production packers. As I mentioned earlier, the completions shown in Figure 7.07, the decision to use a production packer or not may be optional. When we begin to discuss Zonal Isolation, the use of the packers will become required.
As you can see from this discussion, the production engineer must make many decisions for a well completion, even for a completion as basic as that shown in Figure 7.07. The criteria for these decisions were listed in the first bullet list in the Well Design Section: The Overriding Well Design Considerations bullet list. One key aspect of the production engineers’ job is to be kept informed on the latest innovations is sub-surface well technology.
[1] Society of Petroleum Engineers technology website: Petrowiki [77]
7.5.2: Liner Completion
As we discussed earlier, barefoot completions normally target hard, consolidated reservoir rocks. Wells in reservoirs that are susceptible to sand production will require different well completions. For wells requiring sand control, we can use Open-Hole Slotted Liner Completions, Open-Hole Screen Completions, or most commonly, Gravel Pack Completions.
A liner is a casing string that does not go to the surface. A typical Cemented Liner Completion is shown in Figure 7.09 (A). This particular completion does not offer any sand control capability but is included here to introduce the concept of a liner. As we can see from this figure, the liner does not go to the surface but is hung from a Liner Hanger. The cemented liner completion has many of the advantages of a Cased and Perforated Completion (to be discussed) but at a reduced cost. Because the liner in this completion is cemented in-place, (A) it does not represent an open-hole completion and (2) it requires perforations for the well to access the reservoir.
The other completion in Figure 7.09 (B) either the Slotted Liner Completion or the Screen Completion, is an open-hole completion and does offer some sand control capability. Note that we have not cemented the slotted liner or screen set across the reservoir, so these are open-hole completions, but not barefoot completions.
A slotted liner is a liner with pre-milled slots, while a screen is a liner with pre-milled holes. These liners do not require perforations to achieve access to the reservoir. Figure 7.10 provides a more detailed illustration of these liner types.
There are many applications for slotted liners and screens but in the context of this discussion, they provide partial sand control with the physical dimensions of the openings acting as filters against the sand production. This sand control, however, is limited because the openings may eventually plug, causing a reduction in the oil rate.
The most common method of sand control is with gravel pack completions. Two examples of gravel pack completions, one cased and perforated completion and one open-hole completion, are shown in Figure 7.11. In these completions, gravel is placed either between a slotted liner (or screen) and the casing (or sandface) to act as a filter for the formation sand.
The gravel is selected to have good permeability so as not to create a significant pressure drop through the gravel pack and to have good filtering capability. This gravel is often treated with resin to improve its filtering capability.
There are many variants to the gravel pack, such as pre-packed liners or screens (two concentric slotted liners or screens with gravel pre-packed between them) or frac-pack (combination of hydraulic fracturing and gravel packing [2]. This further illustrates the need for the production engineer to work with the oilfield service providers and manufacturers to be aware of all technology innovations. In fact, a significant portion of the production engineer’s time is working with the service companies and manufactures to develop solutions for the completion needs of their wells.
I have included the link to an article from the Schlumberger Oilfield Review with a lot of good information on sand control and frac-packing:
- Schlumberger Oilfield Review [2]: Frac Packing - Fracturing for Sand Control [78]




[2] Schlumberger Oilfield Review: Frac Packing: Fracturing for Sand Control [78]
7.5.3: Cased and Perforated Completion
An example of a Cased and Perforated (“Cased and Perf’ed”) Completion across a single-layer reservoir is shown in Figure 7.12.
The advantages of a cased and perforated completion in the well (Figure 7.12) include:
- in single-layer reservoirs, a cased and perforated completion is a simple, durable completion;
- for multiple-layer reservoirs, a cased and perforated completion allows for zonal isolation for different zones;
- for multiple-layer reservoirs, a cased and perforated completion allows selective stimulation (different stimulation treatments for different reservoir zones);
- very flexible with many possible cased and perforated completions available for the same problems.
The disadvantages of a cased and perforated completion in the well (Figure 7.12) include:
- the costs of the perforating thick reservoir zones may be excessive;
- well logs for future reservoir evaluation, workover planning, or determination to Plug and Abandon the well are limited to Cased Hole Logs (subset of well logs that are not impacted or are designed not to be impacted by the presence of the casing);
- deepening of the well is more difficult than in open-hole completions.
As alluded to throughout the lesson, casing is high quality steel pipe that is major structural part of the oil or gas wells. Off the shelf, the casing has no openings and, consequently, requires Perforation to gain access to the reservoir. There are many grades and specifications for the casing steel quality. The objectives of the casing are:
- provide wellbore stability;
- protect natural aquifers from work fluids and produced fluids;
- control well pressures during drilling, production, and workovers;
- aid in zonal isolation in cased and perforated well completions.

All modern wells use strings of multiple casing. The casing strings that can be used in the oil and gas wells include:
- conductor casing
- surface casing
- intermediate casing
- production casing
- liner
- liner tie-back casing
Several of these casing strings are shown in Figure 7.13. We will discuss the different casing strings and their roles in drilling the well in Lesson 8 when we discuss drilling operations. In our current discussion on cased and perforated completions, however, we are referring to the production casing. The role of the production casing is to:
- aid in zonal isolation;
- protect the wellbore and the outer casing strings from reservoir pressures;
- protect the well and environment in case of a tubing leak.

Cased and perforated wells are completed by first drilling through the reservoir (or sometimes a little deeper than the bottom of the reservoir). The production casing is then run and cemented in-place. Next, the tubing string is run, and all packers are set. Finally, the perforation guns are run and fired to create the access to the reservoir.
A perforation gun is an array of shaped charges that can be arranged in many configurations to achieve the objectives of the well. The perforation guns can be conveyed (deployed) either on wireline (wireline conveyed perforation guns) or on the tubing itself (Tubing Conveyed Perforation, TCP, guns). Figure 7.14 shows a typical TCP gun.
Cased and perforated completions provide the highest level of control for the well, and when used in conjunction of systems of Packers and Bridge Plugs, are capable of providing Zonal Isolation across multiple reservoir zones.
We have already discussed packers earlier in the lesson (see Figure 7.08). As I stated, packers provide isolation in the annulus of the well. On the other hand, bridge plugs provide isolation inside the tubing of the well. Figure 7.15 shows a picture of a bridge plug. The bridge plug can either be conveyed on a wireline or with a workover string. The sealing element of the bridge plug is then set inside the tubing to create the isolation. A bridge plug can be either retrievable or permanent.

We are now in a position to discuss the role of well completions and Zonal Isolation. I think many of the concepts on zonal isolation that we discussed earlier in the lesson will become much clearer starting from this point.
In our earlier examples, Figure 7.07 through Figure 7.12, we considered a reservoir with a single layer or zone. Now, let’s consider a reservoir with two reservoir zones with the possibility of producing unwanted fluids from one or both of the zones as shown in Figure 7.05 and Figure 7.06.
If we know that water will be produced from the lower reservoir interval (a common problem based on the density of water compared to that of gas or oil), then we may consider a well completion such as that shown in Figure 7.16. This completion is a common completion when we are certain that water will enter the well in the lowermost zone.
In Figure 7-16 (A), the well is initially completed with no bridge plug installed. The Blast Joint shown in this figure is a thicker walled / stronger section of tubing that is placed across all perforations in multiple zone completions to protect the production tubing string from erosion due to the jetting action of produced fluids through the perforations. In the configuration shown in Figure 7.16 (A), oil production is allowed from both reservoir zones with the fluids from the lower zone, Reservoir Zone 1, being produced through the tubing and fluids from higher zone, Reservoir Zone 2, being produced through the Annulus (space between the tubing and casing).
At some later date, water production occurs from the lower reservoir zone, Reservoir Zone 1, from one of the water sources shown in Figure 7.5. When this water production becomes too excessive, a bridge plug can be run through the tubing on wireline and seated at the appropriate depth as in Figure 7.16 (B). This is what we refer to as zonal isolation which we use to isolate production of unwanted fluids.
The action of running and seating the bridge plug at a date after production has begun is referred to as a Well Intervention or a Workover. In the case of this example, this is specifically referred to as a Water Shut-Off Workover. Since we are able to the run the bridge plug on a wireline through the tubing (not requiring a drilling rig), we can also refer to this as a Wireline Workover or a Through-Tubing Workover.

For the well’s initial completion Figure 7.16 (A), water production from the lower intervals (as opposed to water production from higher layers – see Figure 7.05) may be assessed prior to drilling the well by the behavior of Offset (neighboring) wells or with open-hole logs and Drill Stem Tests (DSTs) after drilling the well. If the well is in an exploratory geologic basin or new field or reservoir, then you need to incorporate flexibility into completion designs of the early wells.
The advantages of this completion (Figure 7.16) are:
- produce oil at high rates due to flow through both the tubing and annulus resulting in faster payout for the well and the possibility of improved long-term economics;
- provide the ability to selectively isolate (shut-off) the bottom zone, Reservoir Zone 1, with a relatively inexpensive wireline workover.
The disadvantages of this completion (Figure 7.16) are:
- the upper zone cannot be produced through the tubing;
- only the zone serviced by the tubing can be isolated with a relatively inexpensive bridge plug;
- working over the upper zone requires the temporary shut-in of both zones;
- the casing is subjected to higher pressures (the pressure of Reservoir Layer 2), corrosion, and erosion from production;
- the potential for tubing leaks to develop if a differential pressure exists due to differential reservoir pressures;
- only the lower zone (the zone being produced through the tubing) can be assisted with artificial lift;
- sand production from the upper zone may create sand-fill in the annulus and cause stuck pipe if the tubing is attempted to be pulled (a Tubing Change-Out Workover).


To help illustrate the flexibility of the cased and perforated completion, if water is known to be produced from the upper layer, Reservoir Zone 2, then there are tools available (cross-over valve/choke) which can be used to change the flow paths for the produced fluids. That is, at the time of implementing the original completion, if it is suspected that water production may come from the upper zone, then a cross-over valve can be installed to have the fluids from the lower interval, Reservoir Zone 1, enter the well as in this figure but cross-over to the annulus up-hole, while the fluids from the higher interval enter the well as seen in the figure but cross-over to the tubing. In this case, we would be able to isolate the upper zone (now produced through the tubing) with a bridge plug, but not the lower zone (now produced through the annulus).
Again, to further illustrate the flexibility of the cased hole and perforated completion, we can discuss another well completion for this well. From the list of disadvantages for this completion, we see that we are subjecting the casing to high levels of well stress (high pressures, possible corrosion, and possible erosion). If a critical objective of the well is to protect the casing from these well stresses, then the well completion shown in Figure 7.17 may be considered.


This example shows the same two-zone reservoir as in the earlier example (Figure 7.16). In this completion, we have used a Packer – Tail-Pipe Assembly to provide zonal isolation of the water prone, lower layer. This completion, however, results in commingled (mixed) production from the two layers in the tubing. Commingled production may result in production problems if the fluid chemistries in the produced fluids are incompatible. Wax or asphaltene deposition may occur from the two oils if they are significantly different, while scale deposition from produced waters may occur it the chemistries (dissolved solids) of the produced waters are significantly different.
The advantages of this completion (Figure 7.17) are:
- there is no annular flow, so there are no issues with high pressures, corrosion, or erosion acting on the casing;
- the pressure gradient in the annulus and tubing are approximately equal which protects the tubing from tubing leaks.
The disadvantages of this completion (Figure 7.17) are:
- lower production rates – both reservoir zones are being produced through a single tubing string. The smaller cross-sectional area for flow creates a larger pressure drop in the tubing and restricts the total production from the well;
- production from the two reservoir zones is commingled;
- only the lower zone can be isolated with a relatively inexpensive bridge plug.
We can design a third completion for this well and two-zone reservoir which addresses some of the disadvantages of the packer – tail pipe assembly. This type of completion is referred to as a dual-string completion and is shown in Figure 7.18.

In Figure 7.18, we have completed the well with two tubing strings. The key to this completion is the dual-packer. This type of completion can only be run if the original wellbore and production casing have sufficient Inner Diameters to support this equipment and the tools required to run this equipment. This issue is typically considered during the design and planning stage of the well, and if a dual-string completion is to be used in the well, then a larger diameter well can be drilled.
A detailed schematic of a dual packer is shown in Figure 7.19.
The advantages of this completion (Figure 7.19) are:
- there is no annular flow, so there are no issues with high pressures, corrosion, or erosion acting on the casing;
- the pressure gradient in the annulus and tubing are approximately equal which protects the tubing from tubing leaks;
- wireline workovers practical for both reservoir zones;
- production from the two reservoir zones is not commingled;
- both zones can be isolated with a relatively inexpensive bridge plug.
The disadvantages of this completion (Figure 7.19) are:
- expensive completion (two tubing strings);
- the dual string completion is a complex well completion;
- these completions can only be run if the wellbore and production casing have sufficiently large inner diameters;
- lower production rates – production rates are lower because the cross-section to flow is further reduced;
- logging the well may be problematic as logging tools must be available for the restricted dimensions in these completions.
To this point, we have limited our discussion to two-zone reservoirs. I will provide one last example of multi-zone well completion using Sliding Sleeves. This multi-zone completion can also be used for the two-zone reservoir example that we have been discussing. A sliding sleeve completion for a multiple zone reservoir is shown in Figure 7.20.
A sliding sleeve is a device that is run as part of the tubing string that can be shifted to an open position to allow communication between the tubing and annulus or shifted into a closed position to prevent tubing-annuls communication. The sliding sleeve can be shifted to the open or closed position multiple times using wireline or coiled tubing. In this completion, the lowest reservoir zone can be isolated with a bridge plug.

The advantages of this completion (Figure 7.20) are:
- there is no annular flow, so there are no issues with high pressures, corrosion, or erosion acting on the casing;
- the pressure gradient in the annulus and tubing are approximately equal which protects the tubing from tubing leaks (the sliding sleeves themselves may leak);
- all zones can be isolated with a relatively inexpensive wireline or coiled tubing workover.
The disadvantages of this completion (Figure 7.20) are:
- high costs for multiple sliding sleeves and packers;
- lower production rates – production from all reservoirs zones flow through a common tubing string;
- the sliding sleeve completion is a very complex well completion (sliding sleeves and packers susceptible to failure);
- difficulty in monitoring performance of individual reservoir zones.
In the bullet list of overriding Well Design Considerations, we listed simplicity as one of the overarching goals for the well completion. As we have seen in these examples, there may be number of completions that can be used to achieve the specific objectives of the well: sand control, unwanted fluid control, etc. As we have also seen, these well completions can get very complex. One measure of the complexity of the completion is by the number of packers that are required by the completion. Remember, any piece of equipment put into a well; a packer, a bridge plug, a sliding sleeve; can fail. By keeping the completion design simple we are reducing the possibility of the entire completion failing based on the failure of one key component.
We are always trying to make our completions as simple as possible with the ability to achieve the completion objectives: sand control, water control, gas control, amongst others. When we design the completion, we can try to reduce the complexity of the completion by grouping layers in the reservoir. If several adjacent reservoir layers act in unison, then we can reduce the complexity of the completion by grouping the layers as if they were a single layer.
7.6: Tubing Size
We have just considered two design aspects of a well: the orientation of the well and the well completion design. A third aspect of the well design is the tubing size. In Lesson 4 and Lesson 5, we discussed the stabilized production rates from oil wells and gas wells, respectively. Ideally, we would like to design the size of the well tubing to be capable of producing all of the oil or gas without creating a bottleneck in the production. In those lessons, we saw that the inflow performance relationship, IPR, could be represented by the general equation (formerly Equation 4.41):
Where:
- is either the oil production rate (Table 7.01) or gas production rate (Table 7.02):
- Oil: STB/day
- Gas: SCF/day
- is the Productivity Index of the well (see Tables for details):
- Oil: STB/(day-psi)
- Gas:
- Pressure Approach: SCF/(day-psi)
- Pressure-Squared Approach: SCF/(day-psi2)
- Pseudo-Pressure Approach: SCF/(day-psi2/cp)
- Rawlins and Schellhardt Backpressure Approach[3]: SCF/(day-psi2n)
- Drawdown, or its equivalent (see Tables for details):
- Oil: psi
- Gas:
- Pressure Approach: psi
- Pressure-Squared Approach: psi2
- Pseudo-Pressure Approach: psi2/cp
- Rawlins and Schellhardt Backpressure Approach[3]: psi2n
In Lesson 4 and Lesson 5, we assumed that we knew the flowing pressure, , or its equivalent, , etc. in Equation 7.01. With that assumption, we were able to calculate the flow rate from the reservoir to the well. What we did not consider at that time was the impact of the tubing and completion.
| Steady-State Flow Regime | Pseudo Steady-State Flow Regime | |
|---|---|---|
| Pressure Distribution | ||
| In terms of at the external radius, , of the drainage volume | ||
| Drawdown | ||
| Productivity Index |
||
| IPR | ||
| In terms of in the interior of the drainage volume | ||
| Drawdown | ||
| Productivity Index |
||
| IPR | ||
| [A] Note, we did derive the equations in the shaded cells, but they are included for future reference. | ||
| In Terms of Pressure including Damage or Stimulation: All pressures greater than 3,000 psi |
||
|---|---|---|
| Steady-State Flow Regime | Pseudo Steady-State Flow Regime | |
| Drawdown | ||
| Productivity Index |
||
| IPR | ||
| In terms of Pressure including Damage or Stimulation: All pressures greater than 3,000 psi |
||
|---|---|---|
| Steady-State Flow Regime | Pseudo Steady-State Flow Regime | |
| Drawdown | ||
| Productivity Index |
||
| IPR | ||
| In terms of Pressure-Squared including Damage or Stimulation: All pressures less than 2,000 psi |
||
|---|---|---|
| Steady-State Flow Regime | Pseudo Steady-State Flow Regime | |
| Drawdown | ||
| Productivity Index |
||
| IPR | ||
| In terms of Pressure-Squared including Damage or Stimulation: All pressures less than 2,000 psi |
||
|---|---|---|
| Steady-State Flow Regime | Pseudo Steady-State Flow Regime | |
| Drawdown | ||
| Productivity Index |
||
| IPR | ||
| In terms of the Real Gas Pseudo-Pressure including Damage or Stimulation: Valid over the entire pressure range |
||
|---|---|---|
| Steady-State Flow Regime | Pseudo Steady-State Flow Regime | |
| Drawdown | ||
| Productivity Index |
||
| IPR | ||
| In terms of the Real Gas Pseudo-Pressure including Damage or Stimulation: Valid over the entire pressure range |
||
|---|---|---|
| Steady-State Flow Regime | Pseudo Steady-State Flow Regime | |
| Drawdown | ||
| Productivity Index |
||
| IPR | ||
| The Rawlins and Schellhardt Backpressure or Deliverability Equation[1] | ||
|---|---|---|
| Steady-State Flow Regime | Pseudo Steady-State Flow Regime | |
| IPR | ||
As we saw in Lesson 6, the well hydraulics in the tubing is dependent on the production rate. For single-phase flow, this dependency was shown in the Darcy-Weisbach Equation (formerly Equation 6.12):
and for multi-phase flow was illustrated during our discussion on the multi-phase flow correlations (see Table 6.04). In that lesson, we discussed topics, such as:
- Multi-Segmented well modeling
- Pressure Traverse Curves, PTC
- Tubing Performance Curves, TPC
A hypothetical tubing performance curve for a 2.0 inch outer diameter (O.D. – remember, the I.D. of the tubing controls the pressure drop, but by convention we quote the tubing size by its outer diameter, O.D.) tubing is shown in Figure 7.21. In the legend of this figure, we see some of the static and dynamic properties that impact tubing performance (see Table 6.04). In particular, we can see the wellhead pressure, , is 100 psi in this example/figure. This wellhead pressure would be the pressure on the gauge of the wellhead shown in Figure 7.13. The flowing well pressure, , in this figure is the solution of the well hydraulics equations (Darcy-Weisbach Equation or multi-phase flow correlation) which represents the pressure at the bottom of the tubing string (y-axis on this plot) that is required to lift the reservoir fluids at a given production rate (x-axis on this plot).
Note, that we can rearrange Equation 7.01 and solve for :
This is the equation for a straight line in with a slope of and a y-intercept of The pressure, , acting as the y-intercept is the average pressure in the reservoir (for pseudo-steady state flow) and would slowly drift downward as the reservoir pressure is depleted with production. For multi-phase flow, we would not get a straight line, but a curve. For our straight-line example, the IPR is the red line in Figure 7.21. The Inflow Performance Relationship (IPR) represents the rate that fluids can be supplied from the reservoir at a given flowing pressure, while the Tubing Performance Curve, TPC, represents the rate that fluids can be received by the tubing and lifted to the surface at a 100 psi . The intersection of these two curves, then, represents the operating point for the well at this wellhead pressure.

If we were to build a well hydraulics model for a well to run sensitivities on the tubing size, then a plot such as Figure 7.22 would result. When I say “… build a well hydraulics model …”, this model can be a simple as a hand calculation model[4] (the industry standard method thirty years ago), an Excel spreadsheet model, or a current generation software model. The details to include in such a model depend on the objectives of the model. Any well model built with an objective of aiding in the completion design would need to include any pressure losses associated with the completion (for example, pressure drop due to flow through the gravel pack, flow through the perforations, or flow through a hydraulic fracture). We will discuss some of these additional pressure drops later in this lesson.
For sizing the tubing of the well, we would simply be able to calculate the associated with going from one tubing size (O.D.) to the next incremental tubing size (O.D.), run the economics to determine if the larger, more expensive tubing size would pay for itself with its incremental production rate (meet corporate economic hurdles), and continue until we found a tubing size (O.D.) that was uneconomic or could not physically fit inside our production casing.
One example that we can use for estimation of the tubing size is the payback time for an incremental increase in the tubing size. The payback time is the time period required to recoup an investment (or, in other words, the time period that the investment ties up our money). If the incremental rate from the IPR-TPC analysis shown in Figure 7.22 is (STB/day), the total incremental cost for increasing the tubing size is ($), and oil price is ($/STB), then the payback time, (days) is:

In this equation, the numerator is the incremental cost of the larger tubing size in dollars, while the denominator represents the daily revenue of the incremental oil sales in $/day. If a detailed estimate of is required, then we can allow the rate to change over time using the decline curve analysis methods discussed in Lesson 4 and Lesson 5 (rather than using a constant based on stabilized rates).
Earlier, I used the phrase “… corporate economic hurdles …;” I can illustrate the concept of an economic hurdle with our definition of payback time, Equation 7.04. Perhaps the company that you work for dictates that all design aspects of the well must pay for themselves in one year or less; then, we could use the IPR-TPC analysis to determine the largest tubing size that yields a from Equation 7.04 that meets this one-year threshold.
When sizing tubing, we must also be aware that there are other considerations to be evaluated. For example, if we plan to run logging tools on wireline or perform a through-tubing workover, then we would need to size the tubing so that the inner diameter, I.D., would be able to accommodate the physical dimensions of the tools that we plan to run plus any tolerances. From the tubing sizes used in this example, 2.0, 2.5, and 3.5 inch O.D., we can see that the dimensions used in oil and gas wells can be important design criteria for the tubing size selection.
[3] Rawlins, E.L. and Schellhardt, M.A. 1935. Backpressure Data on Natural Gas Wells and Their Application to Production Practices, 7. Monograph Series, U.S. Bureau of Mines.
[4] Brown, K.,E.: The Technology of Artificial Lift Methods (Vols. 1 – 4), Petroleum Publishing Co., Tulsa, O.K. (1977)
7.7: Well Stimulation
We can also use the Tubing Performance Curves and Inflow Performance Curves to aid in other decisions concerning the well design. When we complete a well, we may want to consider stimulating the well or applying artificial lift in the original completion design.
We briefly discussed well stimulation when we were discussing the skin factor, in Lesson 4 and Lesson 5. In these lessons, we saw that the skin factor is part of the definition of the productivity index, (see Table 7.01 and Table 7.02) and is positive for damage and negative for stimulation.
We will use two simple models of skin to illustrate its use when considering well stimulation in the completion design. These two simple skin models are:
and
Where:
- is the skin factor, dimensionless
- is the hydraulic fracture length, ft
- is the well radius, ft
- is the permeability of the reservoir, md
- is the permeability of the stimulated zone, md
- is the radius of the stimulated zone, ft
These two skin models are based on different idealizations of reservoir/well system which are shown in Figure 7.23.

Equation 7.05 uses the idealization of the fracture half-length, as an effective wellbore radius. This idealization is valid if the flow patterns in the reservoir are approximately radial away from the fracture. It is observed that typically after some time period, the flow patterns do establish themselves as radial. You can substitute this definition of skin into any of the inflow performance relationships in Table 7.01 or Table 7.02, perform some algebra, and see that the fracture half-length takes the place of the well radius in a well if there is no other skin in that well.
This definition of skin is applicable for the simple modeling of hydraulically fractured vertical wells. Obviously, this simple description of skin would not be applicable for very complex completions such as that shown in Figure 7.01 with multiple fracture stages. For simple completion designs, we can analyze hydraulic fracture treatments with different fracture lengths to determine the optimal fracture length for our well.
Equation 7.06 defines a skin facture in an equivalent, homogeneous drainage area (single-zone reservoir) that would give the same IPR (rate – drawdown pressure relationship) as our actual composite reservoir (two-zone reservoir). In an acid matrix stimulation treatment in formations susceptible to acid (such as carbonate reservoirs – limestones and dolomites), when we acidize the well, the acid travels out radially from the well increasing the permeability as it reacts with the formation. At some point, typically several inches away from the well, the acid is spent and no longer has any impact on the permeability. Therefore, if we start off with a homogeneous reservoir and inject acid into a susceptible formation, then we would create a composite reservoir similar to the one shown in Figure 7.22 (B). Equation 7.06 is called the Hawkins formula.
Note from Equation 7.06 that if we are increasing the permeability, then the skin factor is negative, signifying stimulation. Therefore, we can use this model of skin to analyze acid treatments with acid types and acid volumes (effective ) to determine the optimal acid treatment for our well.
Once we select the optimal tubing size, then we can use the effective skin factors from Equation 7.05 or Equation 7.06 in the IPR equation to perform our IPR-TPC analyses. This may take several iterations if the stimulation treatment design impacts the choice for the optimal tubing size. A typical IPR-TPC Analysis for different stimulation treatments (effective skin values), is shown in Figure 7.23. The payback time for the stimulation treatments can also be determined from Equation 7.04.

7.8: Artificial Lift
Another aspect of well design is the application of artificial lift. When no artificial lift is applied, we refer to the well as a Natural Lift Well or a Naturally Flowing Well (i.e., the higher reservoir pressure is capable of lifting the heavy liquids without any assistance). As the reservoir pressure depletes due to production or the density of the fluid column in the well increases due to increasing water production rates, then artificial lift may be required to produce the wells at economic rates.
Artificial lift refers to the application of pumps or gas injection to assist the lifting of the heavier reservoir liquids. These methods may be applied early in the life of the field or reservoir to enhance the economics of marginal wells or later in the life of the field or reservoir as subsurface conditions change. In addition to increasing the production rates of wells, due to the reduction in the flowing bottom hole pressures of wells, from Material Balance Considerations, artificial lift can also increase the total recovery from the reservoir.
There are several methods of artificial lift including:
- beam pumps (Nodding Donkey, Sucker Rod Pump)
- electrical submersible pumps (ESPs)
- hydraulic pumps
- progressive cavity pumps (PCP pump)
- gas lift
We will only discuss two methods of artificial: ESPs and gas lift. The design of ESPs and gas lift systems can also be considered in the IPR-TPC analysis. To perform the analyses, a segmented well hydraulics model (discussed in Lesson 6) must be designed to generate the appropriate tubing performance curves for use in the analysis. This is done by adding Downhole Devices into our well model. A downhole device is a piece of oilfield equipment with known rate pressure-rate behavior. Current generation well hydraulics software has options for all common downhole devices including (but not limited to) downhole pumps, gas lift valves, chokes, sub-surface safety valves (SSSV), gravel packs, perforations, etc.
A well completion with a downhole ESP device is shown in Figure 7.24. There are two ways to generate the tubing performance curves for ESP wells/completions:
- the horsepower conversion method
- Pump Curve method (a pump curve is a series of curves including the pump head (pressure boost) versus capacity (flow rate), power input (horse power) versus capacity, and pump efficiency versus capacity – all plotted on the same graph). The pump curve method requires that the user supply a pump curve for a specific pump to the model and the software iteratively determines the pressure boost and temperature change for the prevailing well conditions. This method is more accurate than the horsepower conversion method because the pump efficiency is a function of the capacity but is iterative.
I am including the links to a PetroWiki article and a Schlumberger Oilfield Review article on Electric Submersible Pumps.
- PetroWiki [5]: Electrical Submersible Pumps [81]
- Schlumberger Oilfield Review: Defining Electrical Submersible Pumps [82] [6]
The Schlumberger Oilfield Review link (second link) provides a simple schematic of an ESP (Figure 1 in the article) and an example of a pump curve (Figure 2 in the article).
The horsepower conversion method is a simple method to implement because it is non-iterative, so we will continue our discussion using this method. In this method, the pressure boost through the pump (difference between the outlet and inlet pressures) and the temperature change of a fluid going through the pump are defined by:
and
Where:
- 942.86 and 0.185 are equation constants
- is the pressure boost from the pump, psi
- is the temperature increase through the pump, ºF
- is power rating of the pump (power is the rate of work, +W, in Figure 7.24), horsepower
- is the density of the well fluids (mixture), lbm/ft3
- is the pump efficiency (assumed constant in the horsepower conversion method), dimensionless
- is the total production rate of the well fluids (mixture) at the pump height, bbl/day
- is the specific heat of the fluid, BTU/(lbm-ºF)

Figure 7.25 shows a typical Inflow Performance Relationship – Tubing Performance Curve for ESP Optimization and Design. Typically, when optimizing ESPs, we evaluate:
- the size of the pump (horsepower rating)
- the number of pump stages
- the depth of the pump

Gas lift is an artificial lift method in which we install Gas Lift Valves in the tubing to inject gas into the flowing well stream. The lift gas injected is injected down the annulus and enters the tubing through the gas lift valves. The objective of introducing the external gas into the well stream is to lighten the well column.
I am including the link to the PetroWiki [5] article on Gas Lift:
- PetroWiki: Gas Lift [83]
This article contains more details on gas lift than I am covering in the course lessons including discussions on two variants of gas lift: continuous gas lift and intermittent gas lift.
A typical completion with gas lift valves is shown in Figure 7.26. The gas lift device in a well hydraulics model would simply be the gas lift injection rate of the valve against the backpressure of the produced fluids. The Inflow Performance Relationship – Tubing Performance Curve for Gas Lift Optimization and Design looks like the one illustrated in Figure 7.25. When optimizing the gas lift design, the parameters that are typically investigated include:
- the gas lift rate
- the placement of the gas lift valves (particularly the bottom valve)

[5] Society of Petroleum Engineers technology website: PetroWiki [77]
[6] Rick, von Flatern: “Electrical Submersible Pumps,” Oilfield Review, Schlumberger (2015)
7.9: Key Learnings
- The overriding well design considerations are:
- well costs
- tubing and completion longevity
- well simplicity and reliability
- ability to achieve all (or most) of the objectives of the well
- Well objectives determine how a specific well should be designed. Several more common well objectives include:
- sand control for reservoirs made up of unconsolidated reservoir rock or rock susceptible to Fines Movement (movement of fine-grained materials within the rock)
- zonal isolation for reservoirs with multiple zones (to allow each individual zone to be shut in, if required)
- well stimulation for reservoirs with low permeability or susceptible to well damage
- artificial lift for low rate wells
- Five common well design considerations are:
- well orientation
- completion design
- tubing size
- artificial lift
- well stimulation
- Three common well orientations for crude oil and natural gas production are:
- vertical wells
- deviated (or slanted) wells
- horizontal wells
- These well orientations have different applications in field development including costs and the avoidance of surface locations that are costly, environmentally sensitive, unsafe, or lack appropriate infrastructure (road access, water sources, etc.).
- The well completion is defined as the portion of the well that connects the reservoir to the tubing. Three common forms of a well completion are:
- an open-hole or bare foot completion
- a screen or liner completion
- a cased and perforated (a cased and perf’ed) completion
- Sand control is required in wells producing from unconsolidated or weakly cemented reservoir formations. It is required because fines movement caused by the pressure drop (drawdown) in the reservoir and fluid production dragging loose rock material and debris to the well. Production of this loose material may accumulate in the well as sand fill which may cause production, logging, and workover problems for the well.
- Sand is controlled in the well design through the well completion. The most common form of sand control is some form of gravel pack:
- gravel pack (with slotted liner or screen)
- pre-packed liner
- pre-packed screen
- frac-pack
- Unwanted fluid production is defined as the production of fluids other than the fluid(s) for which the well is designed. This may include gas and water from oil wells or water from gas wells. The well is typically designed for the fluid(s) that achieve the highest revenues from the well. Unwanted fluid production may come from:
- lateral fluid migration through the reservoir
- downward coning of gas from a primary or secondary gas cap or upward coning of water from a bottom-water reservoir
- injection from offset injection wells
- Unwanted fluid production is controlled in the well design by a well completion with zonal isolation. By far, the most versatile well completion for zonal isolation is a cased and perforated well completion. Zonal isolation in a cased and perforated well may be controlled with (amongst others):
- packers
- bridge plugs
- sliding sleeves
- Multiple well completions may achieve the desired zonal isolation (i.e., there is no unique well completion for a well). The overriding well design considerations (first bullet point above) are used to select the final well completion.
- Tubing is the conduit for fluids from the completion to the surface. The flow of fluids up the tubing is governed by well hydraulics in the form of a Tubing Performance Curve.
- Plotting the Inflow Performance Relationship (IPR) on the same graph and the Tubing Performance Curve (TPC) is the foundation of nodal analysis. The IPR defines the rate of fluid production from the reservoir at a given flowing pressure, while the TPC defines the that the rate that fluids can be “pushed up” the tubing at the same flowing pressure. The intersection of these two relationships defines the operating point of the well at the current reservoir and tubing conditions. The Inflow Performance Relationship – Tubing Performance Curve analysis (nodal analysis) provides a powerful tool for defining the appropriate:
- tubing size
- well stimulation treatment
- artificial lift requirement
7.10: Summary and Final Tasks
Summary
In this lesson, we discussed five key design aspects for oil and gas wells considered by production engineers:
- well orientation
- well completion
- tubing size
- well stimulation
- artificial lift
In addition, we discussed two common problems with well production: sand production from unconsolidated reservoir formations and production of unwanted fluids. The sources of unwanted fluid production are:
- lateral fluid migration through the reservoir
- downward coning of gas from a primary or secondary gas cap or upward coning of water from a bottom-water reservoir
- injection from offset injection wells
We also saw that we could mitigate these two problems (sand production and unwanted fluid production) with proper well completions. For sand production, the most commonly used completion involves some form of a gravel pack where the gravel acts as a filter against the sand production. For unwanted fluid production, we build zonal isolation into our well completion designs. For these wells, we can use cased and perforated completions, along with systems of packers, bridge plugs, and sliding sleeves to provide zonal isolation to prevent production of unwanted fluids.
For determining the proper tubing size to use in a well, we plotted the Inflow Performance Relationship and the Tubing Performance Curve on the same graph. The intersection of these curves represents the operating point of the well. By testing multiple tubing strings, we can evaluate the impact of tubing size on the operating point of the well and determine those tubing strings that meet our economic hurdles.
Finally, we discussed well stimulation and artificial lift. We saw that the same analysis method could be used for these aspects of the well design. When evaluating well stimulation, we modified the Inflow Performance Relationship with simple skin models to evaluate the impact on the operating point; while for artificial lift, we saw that pump or gas lift devices had to be incorporated into the well hydraulics model to generate the appropriate Tubing Performance Curves for evaluation and optimization in our analyses.
Final Tasks
Complete all of the Lesson 7 tasks!
You have reached the end of Lesson 7! Double-check the to-do list on the Lesson 7 Overview page [84] to make sure you have completed all of the activities listed there before you begin Lesson 8.
Lesson 8: Drilling Engineering - Drilling Contracts, The Rig Crew, and Drilling Rigs
8.0: Lesson Overview
In this lesson, we will begin to discuss the drilling process. In particular, we will discuss:
- the life-cycle of a field or reservoir and the role of the drilling engineer in each phase of production;
- drilling contracts;
- personnel on a rig crew and personnel at the rig site; and
- types of drilling rigs.
We will also see that drilling engineers work on all tasks involving a drilling rig. Typical tasks performed by a drilling engineer include (but are not limited to):
- help to develop (as part of an Asset Team) well proposals for all wells drilled in a field or reservoir;
- help to develop workover proposals for wells requiring major rig workovers;
- combine the well proposals and major rig workover proposals to develop a rig schedule that ensures that the drilling company has enough rig work to warrant a long-term contract (this benefits their own company, the field operator, by having sufficient work to guarantee a long-term contract results in improved contracts rates);
- perform all drilling calculations (drilling fluid specifications, casing depth targets, cement properties, etc.) to develop the rig specifications for all of the work on the rig schedule to ensure the rigs under contract are capable of handling all work on the rig schedule;
- select all equipment: bit size and type, casing and connection grades, drill pipe grades, etc.;
- liaise with the drilling company and suppliers to ensure that off-the-shelf equipment/supplies and long lead time equipment/supplies are available at the appropriate times on the rig schedule;
- liaise with the local, state, and national governments to ensure that all permits are acquired; and
- work at the rig-site to look after the interests of the operating company.
We will see that operating oil and gas companies, even the large integrated major companies, do not drill their own wells. The drilling operations are typically contracted to drilling companies. The drilling contracts discussed in the lesson are:
- day-rate contracts
- turn key contracts
Finally, we will discuss the types of rigs available for drilling oil and gas wells. We will discuss cable tool rigs from an historical perspective and then discuss modern rotatory rigs. We will then finish the lesson by discussing the different rig-types available for off-shore operations.
Learning Objectives
By the end of this lesson, you should be able to:
- discuss the life cycle of a producing oil or gas field;
- describe the role of the drilling engineer during the life cycle of the field;
- compare and contrast the similarities and differences in exploration wells, appraisal wells, delineations wells, and development wells;
- list and explain some of the most important components of a well proposal;
- list and describe the role of a rig schedule in field development;
- discuss the difference between a day-rate drilling contract and a turn key drilling contract;
- list important terms in a day-rate contract;
- list the job responsibilities of key members of an onshore rig crew including:
- drilling contractor personnel;
- operating company personnel;
- service company personnel;
- list the job responsibilities of key members of an offshore rig crew;
- differentiate between a cable tool drilling rig and a rotary drilling rig;
- explain the differences and pros and cons of rotatory table drilling rigs and a top-drive drilling rigs;
- list the major components of a modern drilling rig; and
- identify the differences in the available off-shore drilling rigs.
Lesson 8 Checklist
| To Read | Read the Lesson 8 online material | Click the Introduction link below to continue reading the Lesson 8 material |
|---|---|---|
| To Do | Lesson 8 Quiz | Take the Lesson 8 Quiz in Canvas |
Please refer to the Calendar in Canvas for specific time frames and due dates.
Questions?
If you have questions, please feel free to post them to the Course Q&A Discussion Board in Canvas. While you are there, feel free to post your own responses if you, too, are able to help a classmate.
8.1: Introduction
The typical life-cycle of most oil or gas fields can be classified into five stages:
- Exploration Stage
- Appraisal/Delineation Stage
- Development Stage
- Plateau Stage
- Decline Stage
- Abandonment Stage
Life Cycle of an Oil or Gas Field or Reservoir
The life-cycle is illustrated in Figure 8.01. Drilling engineers are essential during all stages of this life-cycle.

The life-cycle of an oil or gas field starts with Exploration Stage where undrilled acreage is evaluated to determine its potential for future commercial development. During the exploration stage of field development, Exploration Geologists and Geophysicists (amongst others) develop prospects which look promising for future evaluation. Once these prospects are generated, exploration wells are drilled to prove whether hydrocarbons actually exist at the locations identified by the geologists.
The statistical success rate of exploration wells (exploration wells finding commercially viable hydrocarbon reservoirs) is between 25 – 45 percent[1]. Once a well encounters a crude oil or natural gas reservoir, that well is designated the Discovery Well for the reservoir. This starts the beginning of the Appraisal and Delineation Stage of the field development.
During the Appraisal and Delineation Stage of the field development, wells are drilled to provide data for the Development Geologists to evaluate the newly discovered reservoir. Wells drilled in the interior of the reservoir are referred to as Appraisal Wells and are used to gather information from Core Analysis, Well Logging, and Well Tests that can be used to analyze important reservoir properties and create trend maps of these properties, such as, depth, thickness, porosity, water saturation, permeability, etc. Wells drilled towards the periphery of the reservoir are referred to as Delineation Wells and are used determine the areal extent and size of the reservoir. During this stage in the life-cycle, the appraisal and delineation wells produce limited amounts of hydrocarbons. Oil or gas production, when it occurs during the appraisal and delineation stage, is typically limited to the volumes produced during well tests where the wells are allowed to flow for limited periods of time (several days) to determine the production rates that can be anticipated from the reservoir. Additional fluids may be produced if an Extended (long-term) Well Test or if a Pilot Test is run during the appraisal and delineation period.
Once the development geologists and reservoir engineers feel that the reservoir has been adequately appraised and delineated, the Development Stage begins. In the development stage, all of the wells required for initial Field Development Plan are drilled, completed, and tied back to the production facilities. During this period, multiple drilling rigs may be running simultaneously in order to drill and complete all of production wells, injection wells, and, possibly, observation wells required by the development plan in a timely manner.
After the field has been put onto production, the wells produce into production facilities which have a fixed capacity. If the production potential from all of the development wells exceeds the production capacity of the surface facilities, then production will be limited by the capacity of the production facilities. (In other words, the facilities act as a bottleneck in the system, and the wells must be produced below their potentials). As reservoir pressure is depleted, the potential production capacity of the wells declines (due to the reduced drawdown), and they can no longer produce oil at the full capacity of the facilities. (In other words, at some time, the reservoir pressure declines to the point where the wells become the bottleneck in the system.)
The early period of production, when the facility capacity is the bottleneck, is often referred to as Plateau Stage of production because the facility capacity is relative constant over time (barring any upgrades or additions to the facilities). The later period of production, when the well capacity is the bottleneck is referred to as the Decline Stage of production because the well capacity is tied to the reservoir pressure which is continually decreasing with time. Both of these stages are illustrated in Figure 8.01.
While being the more common name, I personally do not like the term “Plateau Stage” because this has somewhat of a passive sound to it. In order to keep the facilities producing at capacity, there is a lot of activity that needs to be performed behind the scenes. From the start of production, the reservoir pressure will decline due to fluid withdrawals. In addition, as time increases, unwanted water or gas production may increase and Well Interventions (Workovers). To keep oil production at the facilities capacity, Infill Wells may need to be drilled; completion designs may need to be altered; wells may need to be stimulated; water or gas shut-off workovers may become necessary; artificial lift may be required, secondary production techniques may be used; etc. So, during this plateau stage, a lot of reservoir management activities may be required to keep the facilities fully utilized. Therefore, I prefer to call this period the Reservoir Management Stage or Managed Plateau Stage of production.
At some point in time, the reservoir management options can no longer keep production at the facilities capacity, and the field production rate will eventually go into decline. During this stage, reservoir management activities are still performed, but with the objective of arresting the decline rate, not keeping the facilities fully utilized.
Finally, at some finite, non-zero production rate, the revenues generated by the oil and gas sales can no longer support the costs of the operations, and the field must be abandoned. This stage is referred to as the Abandonment Stage of the field.
As stated above, drilling engineers are required during all stages of this life-cycle.
[1] Energy Information Administration / OGJ.
8.1.1: Exploration Phase

As discussed earlier, the exploration geologist and geophysicist (amongst others) generate locations for future exploration prospects. Once exploration prospects are generated, drilling engineers work with the exploration geologists to develop the drilling proposal(s) for any Exploration Wells. Exploration wells are wells which are drilled with an objective of proving or disproving the presence of commercial hydrocarbon accumulations. A popular slang term for the first Exploration Well drilled in a geologic basin or region is a “Wildcat Well”.
The drilling proposal is a plan for the well. Normally, an exploration geologist and the drilling engineer take the joint lead role in the development of the well proposal. This proposal typically includes:
- the objectives of the well (the reasons for drilling the well)
- the proposed drilling rig to be used for the well
- the surface location of the rig site (latitude and longitude)
- the well target:
- the bottom-hole location (latitude and longitude) of the well
- the target depth(s) of the well
- directional drilling information
- the wellbore diameter and depth of the wellbore (wellbore diameters will change during drilling operations due to changes in drill bits)
- the specifications for all bits required during drilling operations
- the anticipated geologic cross-section and stratigraphic column during drilling operations
- the pore-pressure profile anticipated during drilling operations (pore pressures versus depth)
- the fracture pressure profile anticipated during drilling operations (formation fracture pressures are the pressures at which the rock will mechanically fail – fracture)
- the casing design and specifications for the well
- the drilling fluid (mud) design for the well
- the well control and safety procedures for the well
- the required data acquisition that is essential for the exploration geologist to appraise the well
- the anticipated time required to drill the well (depth versus time forecast)
- cost estimates for the well:
- one estimate for an unsuccessful well (no hydrocarbons discovered)
- one estimate for a successful well (hydrocarbons discovered) which may include completion costs and additional data acquisition cost (well logs, core data, etc.)
Once a drilling proposal is generated and approved, the drilling engineer coordinates with the drilling companies, service companies, suppliers, and manufactures for all of the equipment required by the well. Some of this equipment may can be purchased “off the shelf” and can be delivered in a relatively short time; while other equipment (Long Lead Time Equipment) may need to be manufactured to specifications developed specifically for the well. This long lead time equipment may take over a year for delivery. The logistics of coordinating the on-time delivery of the equipment for the well is the responsibility of the drilling engineer.
Drilling engineers also interact and coordinate with the company’s Health, Safety, and Environment (HSE) Departments and government permitting agencies to ensure that the well meets the company’s and the government’s HSE guidelines and that all of the government permits are properly obtained.
Only after the required equipment is onsite (or guaranteed to be delivered on time) and all permits are in hand can drilling operations begin. Again, a drilling engineer takes the lead role in all drilling operations. Whenever a drilling rig is required for some operation (drilling, cementing, Major Rig Workover (MRWO)), a drilling engineer will take the lead. Depending on the organization of the company, the drilling engineer who designed the well may not necessarily be the drilling engineer in charge of drilling the well. A company may be organized in a manner where Staff Drilling Engineers are working with the exploration geologists developing drilling proposals and developing the plans and logistics for the wells, while Field Drilling Engineers are drilling the wells.
8.1.2: Appraisal and Delineation Phase

Appraisal and delineation wells are wells with at least one objective of gaining data to improve the understanding of the reservoir. During this phase of the life-cycle, a rig schedule is typically developed with input from most Asset Team members, but most notably the drilling engineer(s), the development geologist(s), and the reservoir engineer(s). The rig schedule prioritizes the wells to be drilled based on the objectives of the well and the logistics of the well (availability of off-the-shelf equipment and the need for long lead time equipment).
During the appraisal and delineation period, the drilling engineers continue to work with the development geologists to create the drilling proposals. During this phase of the life-cycle, the rig schedule is heavily weighted with drilling activity; however, Plugging and Abandoning (P&A) and Temporary Well Suspension (mothballing the wells for future use as development wells) activities are also included.
During this period, a learning curve for drilling the wells is formed, as the geologic formations to be drilled through and the Drilling Penetration Rates through these formations become understood. Often, this learning curve is applied to the Development Plan and economics of the field or reservoir.
If multiple drilling rigs are available for the project, then the different appraisal and delineation wells in the rig schedule are prioritized and assigned. On the other hand, if a single rig or several rigs are servicing multiple projects, then gaps in the rig schedule are assigned to a project to allow for the timely interpretation of data from a well, so that future wells and well proposals can benefit from that data.
8.1.3: Development Phase
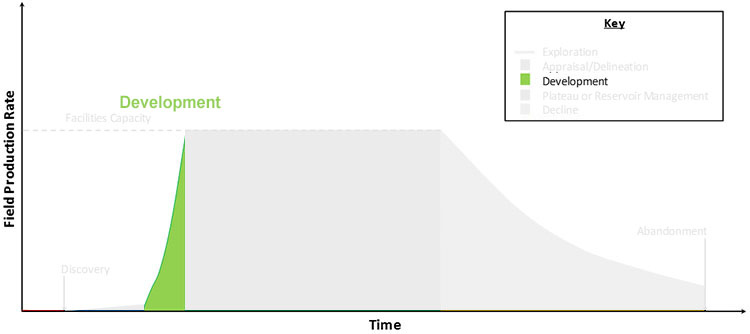
During the development phase, wells are drilled with the primary objective of hydrocarbon production. This is the phase in the field or reservoir life-cycle where the development plan is implemented. There is a strong economic incentive (time value of money) for developing the field or reservoir.
During the development phase of the life-cycle, the rig schedule is almost exclusively dedicated to drilling the wells considered in the original development plan. During development drilling, the learning curve becomes steeper (more is learned over a shorter period) and the drilling times typically become shorter as the drilling engineers and drilling crews make use of the lessons learned from previous wells.
8.1.4: Plateau Phase

As stated earlier, during the Plateau Phases of the field life-cycle, multiple Reservoir Management activities occur. If the field or reservoir is being developed with a Phased Development (development performed in distinct phases), then the drilling of wells required in the later phases of the development occurs.
During this phase, the drilling rig is often used for activities other than drilling. As discussed in earlier, the production of unwanted fluids from the reservoir may require the drilling rig to be used for major rig workovers. These MRWOs require the use of the rig to perform well remediation activities that cannot be performed using a Slickline (a non-electrical conducting wire used to run workover tools), a Wireline (an electrical conducting wire used to run these tools), or coiled tubing (tubing wound on large spools which can be run using a non-rig Coiled Tubing Unit). Workovers requiring a MRWO include some Secondary Cementing Operations (repairing poorly cemented casing sections that were not properly cemented during the original – or Primary Cementing Operations or Squeeze Cementing Operations – Zonal Isolation technique of forcing cement into perforation intervals producing unwanted fluids), pull tubing for tubing change-out operations, pulling the tubing and completion to recomplete the well, deepening the well, milling operations, etc.
8.1.5: Decline Phase

Later in the life of the field or reservoir, the drilling of additional new wells may be required after all phases of the original development plan have been completed and the reservoir management activities focus on arresting the reservoir decline. For example, in order to arrest the declining oil or gas production rates, Infill Drilling may be applied. Infill drilling is a method where the original drainage areas are reduced by drilling new wells between two or more existing wells. Also, in oil reservoirs, Pattern Realignment may be used in Secondary Recovery Operations (gas or water injection) to adjust the producer-injector patterns to recover any oil not recoverable from the original patterns.
As stated earlier, all oil and gas field activities that require a drilling rig are planned and supervised by drilling engineers. As such, the role of the drilling engineer spans the entire life span of the field or reservoir from exploration to decline and abandonment.
8.2: Drilling Contracts
Many people are surprised to learn that the large oil and gas companies that they see in the news or purchase their gasoline from do not drill their own wells. The actual drilling of wells is typically performed by a Drilling Company or Drilling Contractor that specializes in drilling operations. These drilling companies have the expensive equipment (drilling rigs), personnel, and expertise for performing the complex activities associated with oil or gas well drilling. In almost all cases, a Field Operator or Field Operating Company (the oil or gas company operating the field and requiring the services of a drilling company) will develop a contract with a drilling contractor to drill wells in the field. To minimize rig transport time (and cost) and to develop reasonable terms for a good long-term contract, field operators will normally develop a one- to two-year queue of desired work to guarantee to the drilling company. Therefore, the contracting process is performed after the field operator has a mature, robust plan for the field or lease development and a viable rig schedule.
There are many contract types used in the oil and gas industry, but two of the more common contract types are the Day-Rate Contract and the Turnkey Contract. Of these two contract types, the day-rate contract is the more common contract.
In a day-rate contract, the drilling engineers for the operating company design the well, and the operating company leases the drilling rig, its personnel, and routine supplies at a fixed daily rate (Day Rate) from the drilling contractor. This day rate may or may not include fuel (depending on the terms of the contract) and does not include the costs of Capital Goods or special services (such as well logging, cementing, or stimulation). Capital Goods or Tangible Drilling Supplies are tangible items required for the well, such as Casing, Tubing, Completion Equipment, Down-Hole Pumps, etc. (the term “tangible items” refers to items that can literally be touched). Typically, the day rate accounts for approximately one half of the costs required to drill the well. The Total Daily Cost required to drill a well is referred to as the Spread Rate.
To summarize, in a day-rate contract, drilling engineers working for the operating company design the well and plan all of the equipment specifications. In addition, the operating company leases the rig and its rig crew at a specified daily rate (day rate) which accounts for approximately one half of the daily expenditures. The actual daily rate to drill the well is the spread rate.
In a turnkey contract the operating company pays the drilling contractor to design and drill the well for a fixed cost. Thus, the operating company provides the objectives of the well, the desired data acquisition program for the well, the surface location of the well, the bottom-hole location of the well, and the target depth(s) of the well. Drilling engineers working for the drilling company then design and execute the well and coordinate all service work with the Service Companies.
8.3: Rig Personnel
While drilling a well, drilling operations continue 24/7. This is because the drilling contractor would like to maximize the use and revenue from the drilling rig, and the operating company is paying for the rig on a daily basis (for a day-rate contract). Therefore, multiple rig crews are required to run a rig continuously during drilling operations, and multiple companies may be performing Simultaneous Operations (SIMOPS) at various points in the drilling process.
The personnel involved in drilling an oil or gas well include:
- 8.3.1: Drilling Contractor Personnel (Land Rigs)
- 8.3.2: Drilling Contractor Personnel (Offshore Rigs)
- 8.3.3: Operating Company Personnel
- 8.3.4: Service Company Personnel
8.3.1: Drilling Contractor Personnel (Land Rigs)
- Tool Pusher:
The drilling company employee in charge of all drilling and non-drilling operations occurring on and around the drilling rig. He/she is the lead, onsite representative of the drilling contracting company. In addition, the tool pusher is the key contact between the drilling contracting company and The Company Man (lead wellsite representative of the operating company). The Drillers (below) report to the tool pusher. From the drilling company’s perspective, the tool pusher is the principal representative in charge of the safety and environmental aspects of the drilling operations. - Drilling Crew:
- Driller:
The drilling company employee in charge of drilling operations and supervision of a drilling crew. The driller reports to the tool pusher. - Derrickman (one per crew):
The derrickman is typically second in rank in a drill crew behind the driller (Some large offshore drilling crews may have a position of assistant driller ranked between the derrickman and the driller.). In old movies or documentaries, you may have watched scenes of a person working at the top of the Derrick of a drilling rig who is manually moving and handling Drillpipe; this is the derrickman. Historically, this would have been one of the more physically demanding and dangerous jobs on the rig crew. Most modern drilling rigs have automated pipe-handling equipment to preserve safe procedures during current drilling operations. - Roughnecks (several per drill crew):
Experienced members of a drilling crew who may work on the rig floor or up on the derrick. Typical tasks for a roughneck include tending to engines and pumps during operations, coupling or uncoupling Stands of Drillpipe during Tripping Operations into or out of the wellbore, and racking or unracking drillpipe. - Skilled Technicians:
Mechanics, electricians, crane operators, welders, etc., for operating and maintaining specialized rig equipment. - Roustabouts (several per rig crew):
General laborers working on or around the drilling rig. These are entry level jobs on a drilling rig and, in some companies, may be available for summer internships to engineering students. Typical tasks for a roustabout may include unloading, lifting, and hauling materials and supplies used for drilling operations, cleaning and maintaining the rig site (picking up litter, weeding, mowing the grass at the rig site, etc.), maintaining the roads (clearing brush and debris), etc.
- Driller:
8.3.2: Drilling Contractor Personnel (Offshore Rigs)
When drilling offshore, additional crew members are required to handle the marine operations related to the drilling rig. These additional crew members include:
- Offshore Installation Manager:
The Offshore Installation Manager, or OIM, is the chief executive on the offshore installation. The OIM is the final authority for all decisions made on the installation. The operations that are performed under the supervision of the OIM include Drilling Operations, Marine Operations, Mechanical Services, Electrical Services, and Hotel Services. Often, the position of the OIM is assigned to former naval officers or highly experienced offshore tool pushers. - Tool Pusher:
The role of the tool pusher on an offshore installation is identical to that of his/her onshore counterpart. The tool pusher is responsible for all drilling operations. - Barge Master:
The Barge Master (and his/her crew) is responsible for all marine operations that occur on a Mobile Offshore Drilling Unit (MODU). An MODU is drilling rig placed on a mobile marine vessel, such as a ship or barge, that can be moved onto the surface location of the well by either towing or by self-propulsion. The barge master is equivalent to a ship’s captain and is responsible for all marine operations including navigation, hull and deck maintenance, crane operations, helicopter operations, radio operations, supply logistics, etc. - Chief Mechanic:
The Chief Mechanic (and his/her staff) oversees the Mechanical Department and is responsible for the maintenance of all mechanical equipment. - Chief Electrician:
The Chief Electrician (and his/her staff) oversees the Electrical Department and is responsible for the maintenance of all electrical equipment. - Camp Boss:
The Camp Boss (and his/her staff) is responsible for all hotel services on the offshore installation. Work crews on an offshore installation typically work on 7/7, 14/14, or 28/28 day on-duty/off-duty schedules. During their on-duty time on the offshore installation, they must be housed, fed, entertained, etc. The camp boss is responsible for maintenance of all office space, living accommodations, galley (kitchen) services, laundry services, and entertainment services on the offshore installation.
8.3.3: Operating Company Personnel
- Drilling Superintendent:
The operating company employee in charge of drilling operations. The drilling superintendent typically works in a field office away from the rig site and supervises simultaneous drilling operations of multiple wells. The rig-site company man reports to the drilling superintendent. From the operating company’s perspective, the drilling superintendent is the principal representative in charge of the safety and environmental aspects of the drilling operations. The position of the drilling superintendent is typically given to experienced drilling engineers. - Wellsite Personnel:
- Company Man:
The operating company representative at the rig site. This function is typically handled by an experienced drilling engineer or wellsite geologist who looks after the interests of the operating company. In addition, the company man liaises with the tool pusher to ensure the well plans are carried out to the operating company’s specifications and safety standards. - Wellsite Geologist:
An operating company geologist who reviews the geologic progress of the well as it is being drilled. Typical tasks performed by a wellsite geologist include planning and reviewing well logs during Well Log Operations (well logs are records of geological data versus depth used by geologists to evaluate a well); reviewing Logging while Drilling (LWD) or Measurement while Drilling (MWD) data if available (LWD and MWD are relatively recent developments that include logging equipment on the Bottom-Hole Assembly (BHA) of the drill string and are used to obtain real-time logs of the wellbore.); and Mud Logging (the analysis of rock cuttings as they are brought up-hole by the Drilling Fluid or Drilling Mud. The main roles of the wellsite geologist are to keep the company man and drilling superintendent appraised of the progress of the well (particularly as it approaches the reservoir targets), to inform the driller and company man when important geologic Marker Beds may be encountered so new drill bits or drilling fluids can be made ready, and to provide written reports and records to development geologists to aid in their interpretations of the well and reservoir.
- Company Man:
8.3.4: Service Company Personnel
In addition to the operating company and the drilling company, specialized companies, called Service Companies, provide specific well services at the rig-site during certain operations. The service company personnel also form an integral part of the well drilling team.
- Drilling Fluids Engineer or “Mud Man”:
The Drilling Fluids Engineer (often referred to as “a Mud Man”) is a wellsite specialist who ensures that the properties of the Drilling Fluid (often referred to as “Mud”) meet the specifications for the section of the wellbore that is currently being drilled. As the well depth increases, the specifications of the drilling fluid will change as the rock and fluid properties encountered by the well change. The drilling fluids engineer ensures that (1) the Mud Pumps are operating properly, (2) any drilling fluid additives are onsite and are capable of achieving the specifications required by the current and future sections of the wellbore, and (3) all additives are added at the appropriate times (or, if required, the mud is switched out entirely) when well conditions change. The term “mud” is used in oil and gas well drilling because historically the most common water-based drilling fluids were mixtures of water and finely ground, bentonite clays which, in fact, are muds. - Cement Engineer:
The Cement Engineer is a wellsite specialist who ensures that (1) the Cement Pumps are operating properly, (2) cementing operations are performed in a safe manner and are capable of achieving the cementing objectives of the well, (3) the cement properties (rheology, fluid loss, slurry thickening time, slurry setting time, etc.) meet the specifications required for the cementing operation, and (4) cement additives are onsite and can achieve the desired cement properties. During the oil and gas well drilling, Casing must be cemented into place to protect the environment from the wellbore (and to protect the wellbore from the environment). Casing is steel pipe used to isolate the environment from the wellbore and from the drilling operations. During cementing operations, a cement slurry is pumped downward through the interior of the casing and then upward through the annular space between the wellbore and the outer diameter (O.D.) of the casing. The cement is then allowed to set in this annular space. - Logging Engineer:
As discussed earlier, Well Logs or Open-Hole Logs are run periodically during drilling operations (prior to the setting of casing – most importantly over the producing intervals prior to the installation of the production casing string or liner). Well logs are records from measuring devices that are used to evaluate certain properties of the downhole rocks. The logging engineers make sure that all logging equipment is working properly and that all logging tools are accurately calibrated. Typical processes logs measure reservoir properties such as porosity, fluid saturations, and permeability (after calibration with well logs or well tests). - Well Test Engineer (Optional):
Once a well has reached its target formation(s), it may be tested with a Drill Stem Test (DST). In a drill stem test, the formation of interest is isolated using a temporary completion, and fluids are produced through the drill pipe or a DST string. The well is flowed at a predetermined rate-time schedule to estimate reservoir characteristics such as reservoir pressure, reservoir permeability, and anticipated production rates. The main objective of a DST is to determine whether the well is economically viable and warrants a permanent completion or whether the well should be Plugged and Abandoned (P&A’ed). Drill stem tests are typically run on Exploration Wells or Appraisal Wells where reservoir properties may not be fully understood. In Development Wells in reservoirs with known property ranges and property trends, DSTs may not be required to determine whether a well should be completed or not, and that decision can be made from open-hole logs. - Well Completions and Stimulation Engineers:
Once a well has reached its target formation(s) and the decision to complete the well has been made, the well is completed and stimulated (not all wells are stimulated). As we discussed in earlier lessons, stimulation refers to the process of Acidizing or Hydraulically Fracturing (Frac’ing) the well in order to improve the flow conditions near the well. Due to the controversies associated with the hydraulic fracturing process, you may have seen photos or videos of wells being hydraulically fractured in the news or on the Internet. The completions and stimulation engineers coordinate the completions operations with the tool pusher and company man, ensure that the completion or stimulation process meets the objectives of the well, and supervise the crews performing the work. Typically the role of a completions engineer is assigned to a production engineer.
8.4: The Drilling Rig
8.4: The Drilling Rig section of this lesson will cover the following topics:
Note: You can access specific subsections of the lesson by clicking on the links above or continue reading through the lesson using the link below.
8.4.1: Cable Tool Rigs
Cable tool rigs were the first drilling rigs used for hydrocarbon wells. They were used in the United States in the second half of the nineteenth century (1800s) to drill shallow hydrocarbon wells in the Appalachian Region. While these rigs are no longer used in modern oil and gas well drilling, they are of historical note. Cable tool rigs were originally used in the United States for drilling water wells in the early 1800s but had their origins in the percussive drilling techniques used by ancient Chinese and Persian civilizations. They were adapted in the mid- to late-1800s for drilling hydrocarbon wells. Figure 8.02 provides an illustration of a cable tool drilling rig.
| Diagram | Index |
|---|---|
 |
|
| Cable-tool drilling is done by raising and dropping a string of tools on the end of a cable. The up and down motion is imparted by the walking beam. The tools are pulled from or lowered into the hole by winding or unwinding the drill cable on the bull wheel. Casing is raised or lowered by the casing line and calf wheel. The cuttings are removed from the hole by the bailer, which is raised and lowered by the sand line and reel. | |
| Source: Ball, M. W.: This Fascinating Oil Business, The Bobs-Merrill Company, p. 103 (Cable Tool Drilling Rig [94]) |
|
The cable tool itself is essentially a heavy metal chisel that is suspended from a wire cable which, in turn, is attached to a spring pole or Walking Beam (similar to a lever and fulcrum system). The cable tool is repeatedly raised, using the spring pole or walking beam, and allowed to drop (free fall) down the wellbore causing the rock to fail at the point of impact at the bottom of the hole. When enough rock fragments accumulate at the bottom of the wellbore, water is poured into the hole, and Bailers are lowered to remove the rock cuttings and debris.
Historically, bailers were simply buckets used to lift the debris from the wellbore to the surface. Modern bailers are tools which are run on wireline or slickline with a sealed compartment at low pressure. When the compartment is opened, the surge of fluids at hydrostatic pressure into the low-pressure chamber carry the sand and drilling debris into the bailer. The tool is then lifted to the surface.
Cable tool rigs are of historical note because Colonel Drake’s well in Titusville, PA (considered the first well drilled with the specific objective of producing oil) was drilled with a cable tool rig in 1859 to a depth of 69.5 ft. The drilling of Drake’s Well is considered to be the start of the modern oil and gas industry. Cable tool rigs began to be replaced with rotary drilling rigs in the 1890s.
8.4.2: Rotary Rigs
As previously mentioned, rotary rigs began to replace cable tool rigs in the late 1890s. The discovery well for the prolific Spindletop Oilfield in Beaumont, TX was drilled to a depth of 1,039.0 ft with an early rotary rig in 1901 (Spindletop discovery date was January 10, 1901).
In a rotary rig, torque (rotation) is applied to the Drill Pipe or Drill String (hollow steel tubing) with a drill bit attached to the end of the Bottom-Hole Assembly (BHA). As the name implies, the bottom-hole assembly is attached to the bottom end of the Drill String, nearest to the formation being drilled. The drill string is the combined length of drill pipe extending from the rotary system on the drilling rig to the bottom-hole assembly at the bottom of the wellbore). The BHA contains all of the equipment required to drill the current section of the wellbore. This equipment may include Drill Collars (heavy steel tubing used to add weight to the drill bit), directional drilling equipment, LWD or MWD tools, etc.
There are several ways to classify rotary drilling rigs. However, in this class, we will classify them by the location on the rig of the Rotary System. The Rotary System is one of the major systems on the drilling rig and is where the torque is applied. We will discuss two types of rigs with two different rotary systems: a conventional rotary table rig and a top-drive rotary rig.
The following pages will discuss two types of rotary rigs.
- 8.4.2.1: Conventional Rotary Rig or Rotary Table Rig or Kelly Drive Rig
- 8.4.2.2: Top-Drive Rig
8.4.2.1: Conventional Rotary Rig or Rotary Table Rig or Kelly Drive Rig
A conventional rotary rig or rotary table rig or kelly drive rig is a drilling rig where the rotation of the drill string and bit is applied from a rotary table on the rig floor. The conventional rotary rig was the most common rig used during the past century (1900s) and is the drilling rig that you are probably most familiar with from old movies and documentaries. A schematic of a conventional rotary drilling rig is shown in the schematic diagram in Figure 8.03.
| Diagram | Index |
|---|---|
 |
|
| Source: D.T.E. Drilling Components of a Land-Based Rotary Drilling Platform [95] | |
As identified in this figure, the Derrick or Mast (Item 14) is the tall steel structure with its base on the rig floor. On the rig floor the Kelly (Item 19), the Kelly Bushing (not shown), and the Turn Table or Rotary Table (Item 20) are also identified in this figure. These are the components of the Rotary System that provides the torque to the drill string on a conventional rotary rig. A photograph of an actual kelly, kelly bushing, and turn table / rotary table is provided in Figure 8.04(A) while a schematic diagram of the entire assembly is shown in Figure 8.04(B) .
The kelly is a hollow square or hexagonal piece of pipe through which the drill pipe can be passed. This is the pipe marked (I) in Figure 8.04. The kelly is matched to a similarly shaped bushing (square or hexagonal), the kelly bushing, marked (II) in Figure 8.04 which is raised above the rig floor. You can think of the kelly as a hollow square or hexagonal bolt and the kelly bushing as a matching square or hexagonal wrench that turns the bolt. The kelly bushing is set into the master bushing, marked (III) in the photo, with four large metal pins, which in turn sits in the rotary table, marked (IV) in the photo. The rotary table provides the torque required to rotate the master bushing, kelly bushing, kelly drill pipe, and drill bit. The slight rotational blur in the photo implies that the rotary table and kelly were rotating when the photo was taken.
Also shown in Figure 8.04(A) is the Mousehole, marked as (V) in the photo, along with a Joint of Drill Pipe (painted yellow in the lower left-hand corner). The mousehole is the temporary storage location for the next Joint of Drill Pipe to be added to the Drill String. A joint of drill pipe is a 30-foot piece of pipe that is the basic element of the Drill String. Oil and gas companies purchase drill pipe from the steel companies by the joint. Typically, two (a Double) or three (a Triple) joints of drill pipe are connected to form a 60-foot or 90-foot Stands of drill pipe that are racked and stored on the side of the derrick as shown as Item 16 in Figure 8.03 and in the photo in Figure 8.05. Note that the Mousehole is not the same as the Rat Hole (Item 21) in Figure 8.03. On the rig floor, the rat hole is a hole on the rig floor with a large diameter piece of casing extending above the rig floor that is used to temporarily store the kelly when it is disconnected.

Source (Part B): Drilling Formulas: What is Kelly Rig? [97]

8.4.2.2: Top-Drive Rig
Figure 8.06 shows a schematic diagram of a typical top-drive rig. In a top-drive drilling rig, the top-drive (Item 6 in Figure 8.06) is suspended from the traveling block (Item 5 in Figure 8.06) and attached to a guide system (gear train and rail system) on the derrick. The top-drive is an electrical motor that has the ability to travel vertically up and down and to impart torque to the drill pipe. These drilling rigs began to appear in the late 1990s. Although the top-drive supplies the torque for the system, a rotary table is still used to supply stability to the drill string and as a redundant (back-up) rotary system.
The advantages of a top-drive rig are that longer sections of drill pipe can be (1) connected to the drill string when the rig crew is drilling ahead, (2) connected to the drill string when tripping into the hole, or (3) unconnected from the drill string when tripping out of the hole.
As we saw in our discussion of a Conventional Rotary Table Rigs, the next 30-foot joint of drill pipe to be added to the drill string is temporarily stored in the mousehole on the rig floor. This joint of drill pipe is added to the drill string when drilling ahead or tripping into the wellbore. Tripping is the process of running drill pipe into or out of the hole for purposes other than drilling ahead. For example, if a drill bit needs to be changed due to wear, then the entire drill string needs to be pulled from the wellbore (tripping out of the hole), the drill bit needs to be replaced, and the drill string needs to be run back into the wellbore (tripping into the hole) to resume normal drilling operations. You can imagine how much ineffective rig time (in terms of not drilling ahead) is used tripping into or out of the wellbore and making or breaking connections in the drill string–particularly if the well's TD (Total Depth) is 10,000–15,000 feet (or a shallower well has a 10,000-foot horizontal section).
| Diagram | Index |
|---|---|
 |
|
| Source: United States Department of Labor - Oil and Gas Home - Illustrated Glossary Drilling Rig Components [100] Note: On the website linked above, you can select a name from the list or a number on the graphic to see a definition and a more detailed photo of the object. |
|
I would recommend that you go to the website and use the links to get a description of each component of the rig.
The improved efficiencies coming from a top-drive is that an entire 90-foot stand (or triple) of drill pipe can be connected to the drill string rather than a single 30-foot joint. This is because the top-drive can go to the full height of the derrick using the traveling block to connect to the entire stand of drill pipe. Note, however, that not all top-drives use a triple when connecting drill pipe; some use a Double (two joints), while others use a single joint from a mousehole.
Many of the concepts that we have been discussing are best illustrated with a series of YouTube videos and screen captures.
The Drill Training - Run drill pipe through rotary table YouTube clip (1:07) is an animation of how drill pipe connections are made on a conventional rotary rig. As I mentioned, on a conventional rotary table rig, only one joint (30 feet) of drill pipe can be added to the drill string at one time.
Highlights from this video include:
- Figure 8.07: Screen Capture at 9 seconds into the video: Rig Components
- Figure 8.08: Screen Capture at 19 seconds into the video: Use of Slips
- Figure 8.09: Screen Capture at 23 seconds into the video: Use of Mechanical Tongs

In the screen capture shown in Figure 8.07, we see many of the components discussed in this lesson: the kelly, kelly bushing, rotary table, mousehole, and rat hole. Throughout the video, you can see these components of the rig used in action.

In the screen capture shown in Figure 8.08, we see the slips (yellow). As shown in the video, the slips are used to suspend the drill string when it is disconnected from the rig’s hoisting system.
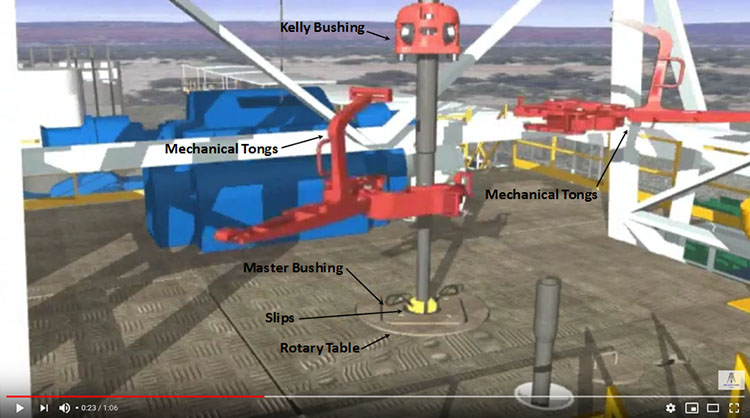
In the screen capture shown in Figure 8.09, we see the mechanical tongs (red). As shown in the video, the mechanical tongs are used to grip the kelly and drill string to aid in uncoupling (unscrewing) the two.
The A Drill Pipe Connection YouTube clip (5:42) below is of several Roughnecks (discussed earlier in this lesson) on an actual rig crew performing the same operations that you saw in the animation. Again, these tasks are being performed on a conventional rotary table drilling rig.
At several points in the video you can see a roughneck Throw Chain around the drill pipe. The Winding Chain is used to apply the torque that is used to screw or unscrew the threads in the drill pipe to couple or uncouple the joints.
What I like about this clip, and the reason that I selected it, was because of the “non-standard operating procedure” that seems to be occurring in the video. Did you spot it?
At around 2:52 into the video, it appears that while two of the roughnecks were trying to remove the slips from the master bushing, the hoist system on the derrick was attempting to assist them by lifting the kelly and drill pipe to release pressure from the slips. Instead of freeing the slips, the hoist appears to have lifted the entire section of the rig floor covering the rotary table, along with the two roughnecks. You can hear someone laughing in the video.
At around 3:31 into the video, one of the roughnecks and the hoist appear to use a piece of drill pipe to tamp the section of rig floor back into place. This piece of drill pipe is then placed into the mousehole as the next piece of drill pipe to be connected to the drill string. This is not a standard operating procedure on the rig floor. After this incident, you can see the rotary table and kelly bushing rotating in the manner discussed in these lesson notes.
In the tripping pipe with top drive YouTube clip (5:12), we will now see a rig crew performing the same operations on a top-drive rig.
In this video, you can see two roughnecks connecting Doubles (two joints) of drill pipe to the drill string as they trip into the wellbore. You can tell that they are connecting doubles by counting the joints as they go into the wellbore. You can also tell that they are tripping into the hole because as they add the new drill pipe, they just run it into the hole and do not drill.
The Making a connection on a top drive triple from the derrick YouTube clip (3:26) is of a Derrickman (discussed earlier in this lesson) making connections on a top-drive rig from the perspective of the monkey board (Item 4 in Figure 8.06).
In this video, the derrickman appears to be connecting Triples (I think that I count three joints of drill pipe looking downward to the rig floor). As I mentioned, this video is taken from the monkey board on the top of the derrick.
The improved efficiency of the top-drive rigs comes from its ability to connect longer sections of drill pipe during tripping and drilling operations. This is done in less rig time and with less cost than a conventional rig. The two major advantages of a top-drive drilling rig are:
- the ability to handle multiple joints (two or three joints) of drill pipe at one time during connecting/unconnecting operations
- the ability to rotate the drill pipe while tripping into or out of the wellbore to avoid Stuck Pipe during tripping operations
Extended Reach Drilling enables wells with long horizontal or near-horizontal lengths to be drilled through the reservoir in a more efficient manner than in the past. These long horizontal wells are one of the technology enhancements that has resulted in the “shale boom” in the U.S. domestic oil and gas industry in formations such as the low permeability Marcellus Shale in western Pennsylvania, Ohio, and West Virginia. The other technological advancement required for the shale boom was the ability to stimulate these extended reach wells with multiple hydraulic fractures (as we discussed in Lesson 7).
8.4.3: Offshore Drilling Rigs
In 2015, offshore oil production accounted for approximately 30 percent of global oil production[2]. The more prolific offshore regions of the world include the U.S. Gulf of Mexico, the North Sea, the Arabian/Persian Gulf, the Caspian Sea, offshore West Africa, amongst others. The principles of rotary drilling for offshore oil and gas are essentially the same as those of onshore drilling; however, the rigs used for offshore drilling must be placed on sea-going vessels or on fixed Production, Drilling, and Quarters platforms.
When placed on sea-going vessels, the drilling rig forms an integral component of a Mobile Offshore Drilling Unit (MODU). The MODUs discussed in this lesson are Jack-Up Rigs, Semi-Submersible Rigs, and Drill Ships. Drilling rigs on fixed Production, Drilling, and Quarters (PDQ) platforms are not mobile, and hence, not considered to be a Mobile Offshore Drilling Unit.
Before we continue with this discussion, we must make a distinction between an offshore platform and an offshore rig; they are not synonymous. An offshore oil or gas platform (or some other offshore facility such as a Floating Production Storage and Offloading (FPSO) vessel) is used for production, injection, artificial lift, fluid separation and treating, fluid export, and possibly drilling. In other words, an offshore platform is used for all operations associated with the extraction of hydrocarbons from offshore oil or gas fields. On the other hand, an offshore rig is used exclusively for drilling and workover operations.
The following pages will discuss four types of offshore drilling rigs.
- 8.4.3.1: Jack-Up Rig
- 8.4.3.2: Semi-Submersible Rig
- 8.4.3.3: Drill Ships
- 8.4.3.4: Drilling Rigs on Fixed Production Platforms
[2] U.S. Energy Information: Offshore production nearly 30% of global crude oil output in 2015
8.4.3.1: Jack-Up Rig
A jack-up rig is a floating drilling rig with (typically) three retractable legs which can be raised while the rig is moved onto location (either self-propelled or towed) and lowered into the seabed to jack-up (lift) the rig to a safe height above the water level, cantilever the rig to the desired surface location of the well, and provide a stable platform for drilling operations. Figure 8.10 shows a jack-up rig with its legs retracted being towed onto location.
When on location, the legs are lowered until they reach the seabed. Once the legs reach the seabed, further extension allows the rig itself to be raised to the desired height above the water level and preparations for drilling can be commenced. The legs on a jack-up rig can be up to 500 ft. in height. Considering a 100 ft air space between the waves and hull of the rig, this allows for water depths of approximately 400 ft for drilling operations. The rotary rig on a jack-up rig can either be a conventional kelly drive rig or a top-drive rig.

Jack-up rigs are used to drill wells in shallow waters, typically less than 400 ft of water, and can be used to drill wells to a Total Depth (TD) of 30,000–35,000 ft. Due to their mobility, jack-up rigs can be used to drill exploration wells, appraisal wells, and development wells.
Below are three YouTube videos of jack-up rigs in action. The first YouTube video, Jackup Drilling Rig How Does It Work? (1:36), is an animation showing a jack-up rig being towed to a Well Jacket (the small structure to the right of the video). A well jacket is an offshore structure that typically contains a minimal amount of production equipment, such as, multiple trees/well heads, minimal surface production equipment (a test separator, metering equipment, etc.), and a helideck. A Tree (or Christmas Tree) is the system of valves, chokes, and gages that sits on the top of the well head and is used to direct, control, and shut-in production during the well’s productive life. An illustration of a Christmas Tree and well head is shown in Figure 8.11.
Multiple deviated wells are drilled from the well jacket to various bottom-hole targets and depths. In earlier lessons, we discussed that deviated wells are the most common well orientations used offshore. The clip you are about to watch illustrates why this is the case
Since the well jacket is already in place in this video, we know that the jack-up rig will be drilling a Development Well. This is because the oil company already knows that hydrocarbons are present below and have invested in the well jacket. Also shown in this clip is a supply boat arriving at approximately 1:12 into the video.
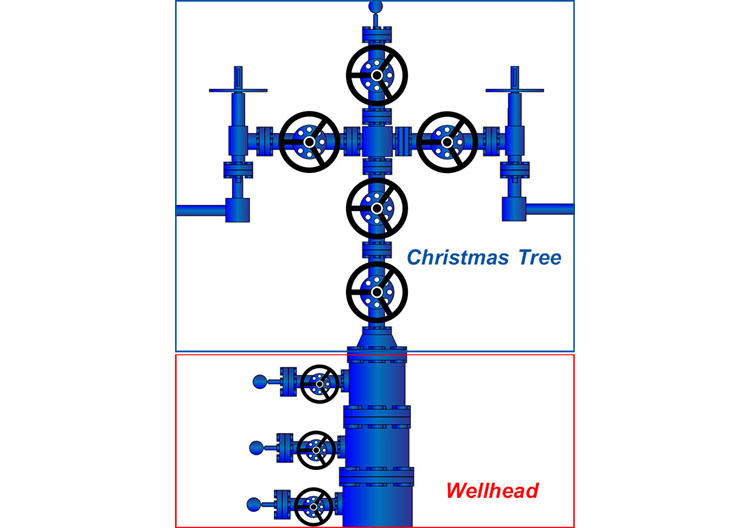
In the second YouTube video, Jack-up Rig (0:46), both real footage and animations are included. This video clip seems to be showing two distinct operations. In the first segment (real footage) from 0:00 to 0:12, we see an actual jack-up rig in-place next to two small offshore structures. The structure nearest to the drilling rig is a well jacket as discussed earlier. The second small structure connected by the bridge is a small production platform. These structures are referred to as Bridge-Linked Structures. Since these two structures are present, we know that the jack-up rig is drilling a Development Well.
The animation then begins at 0:12 and appears to show a rig drilling an exploration or appraisal well. We know this because there are no production facilities present in the animation. In fact, the narrator states “… if they hit oil, they will cap the well, jack the rig down, and then tow it to its next location … and a permanent drilling platform will take over pumping the oil.”
I selected this video for two reasons:
- It shows footage of an actual jack-up rig and two offshore structures
- It shows an exploration or appraisal well being drilled from the jack-up rig
I will have a little commentary on some of the narrator’s comments after you watch the video.
I did have a few issues with the narrator in this video. Now that you are an “insider,” did you catch some mistakes made by the narrator? Everything was going well until he stated “… and a permanent drilling platform will take over pumping the oil.” What he should have said was: “… and an offshore facility will take over producing the oil.” As we just learned, a platform produces the oil (this “platform” may be a simple well jacket as we have seen, a large complex Production, Drilling, and Quarters (PDQ) Platform, or a Floating Production, Storage, and Offtake (FPSO) vessel). Regardless, a “permanent drilling platform,” if they existed, would drill, it will not “pump” anything (except for fluids required in drilling, cementing, completion, or workover operations).
Second, the narrator assumed that the discovery well would need to be pumped. As we have seen in earlier lessons, not all reservoirs need artificial lift; many flow naturally. The decision to use artificial lift on this potential discovery will be up to the production engineer and the Asset Team.
The third YouTube video, Haven jack-up test (2:59), is actual footage of a jack-up rig being jacked up, either in a fabrication yard or for periodic maintenance. I selected this video because it shows actual footage of the jack-up and jack-down operations.
8.4.3.2: Semi-Submersible Rig
A Semi-Submersible Rig or a “Semi-Sub” or a “Semi” or a “Floater” is a drilling rig that is used to drill wells in water depths inaccessible to jack-up rigs (water depths greater than 400 ft). Semi-submersible rigs are buoyant and, unlike jack-up rigs which rest on the seabed, float during drilling operations. A semi-submersible rig is a drilling rig that is situated on a deck space that rests on several columns which, in turn, are attached to floating pontoons. Figure 8.12 shows a semi-submersible drilling rig.
During transport (either self-propelled or towed), the pontoons allow the vessel to float in the water until it is on location. Once on location, water is used as ballast to partially flood the pontoons and columns to allow them to sink to a position below the water level. This is done to create greater stability during drilling operations by adding mass to the vessel and providing it with a deeper draft. The columns provide additional stability to the vessel during drilling operations due to their small cross-sectional area as little wind, wave, or tidal energies are imparted to the columns and the vessel (this is called Wave Transparency). In addition, a system of Thrusters (high energy propellers) is used to control the pitch, roll, and yaw of the vessel and to provide Dynamic Positioning to keep the rig at the same surface location during drilling operations. The thrusters are the yellow devices under the pontoons in Figure 8.12. Semi-submersible drilling rigs are considered to be the most stable of the deeper water MODUs.
Semi-submersible rigs are used to drill wells in water depths up to 9,500 ft. The current world record water depth for a semi-submersible rig using dynamic positioning is 9,472 ft.[3] Due to their stability, semi-submersible rigs are also preferred in harsh offshore environments. Semi-submersible drilling rigs are capable of drilling wells to a TD (total depth) of 30,000 – 35,000 ft.
I have included a video below, Maersk Drilling - Ultra deepwater semi-submersible rig - Maersk Developer (17:48), showing an animation of a semi-submersible drilling rig. The drilling rig shown in this animation is the Maersk Developer rig, a very modern rig (Note: rigs like this one do exist – this is not a “rig-of-the-future” video.). This is a promotional video, so you may need to overlook its commercial nature. I selected this video clip because it ties together a lot of the concepts that we have discussed in this and past lessons; it shows the interior of the rig; and it discusses many of the rig specifications considered in the design (remember, you as a drilling engineer will need to coordinate with the drilling company for the proper rig specifications when contracting a rig).
In the video, the narrator discusses two concepts that we have not gone over yet, a Riser and a Moon Pool. A Riser is a piece of vertical pipe that attaches to the Tree (see Figure 8.11) and, in the case of a Subsea Tree (a tree that sits on the seabed) extends upward to the water surface. Risers act as conduits for drilling and completion fluids during drilling operations or as conduits for produced fluids during production operations.
A Moon Pool is a hole in the deck of a ship or vessel that allows for communication from the deck to the water surface. I will discuss the moon pool in more detail when we discuss Drill Ships. The rotary system of the drilling rig sits above the moon pool. It is where the drill pipe goes from the rig through the deck and into the water.
Here is the link to the video (17:48) on the “Maersk Developer,” a semi-submersible drilling rig:
[3] PetroWiki: Semi Submersibles [109]
8.4.3.3: Drill Ships
As the name implies, a Drill Ship is a sea-going ship that is specifically modified to perform deep water drilling operations. They are equipped with an on-board drilling rig that sits above a Moon Pool (a hole in the ship’s structure from the main deck through to the hull). The Moon Pool (or “Wet Deck”) allows drill pipe to extend from the rotary system of the drilling rig, through the structure of the ship, through the hull, into the water to the sea floor, and into the wellbore. Figure 8.13 provides a picture of a drill ship.
Drill ships are used for deepwater drilling in regions with little onshore logistical support. Drill ships can typically store large quantities of supplies which allows for their use in more remote regions. Consequently, drill ships are often used for exploration well drilling in remote, deep water locations.
Like semi-submersible drilling rigs, drill ships are kept on location during drilling operations with the use of a system of dynamic positioning thrusters. As previously discussed, however, semi-submersible drilling rigs are considered to be a more stable drilling platform than drill ships.
8.4.3.4: Drilling Rigs on Fixed Production Platforms
In addition to the Mobile Offshore Drilling Unit (MODU) discussed so far, offshore wells can be drilled from fixed production platforms. Figure 8.14 shows a picture of the Hibernia Platform in the Atlantic Ocean offshore of Newfoundland, Canada. As seen in this photo, the Hibernia Platform has two drilling rigs for simultaneous drilling or workover operations. In addition to these rig activities, the Hibernia Platform handles production activities such as fluid separation and processing.

8.5: Key Learnings
- There are six stages in the life cycle of a producing oil or gas field
- Exploration Stage
- Appraisal/Delineation Stage
- Development Stage
- Plateau Stage
- Decline Stage
- Abandonment Stage
During the Exploration Stage, wells are drilled with the objective of proving the existence or non-existence of oil or gas at locations deemed promising by geophysicists and exploration geologists. During the Appraisal/Delineation Stage, wells are drilled with the objective of gaining information about the reservoir. The appraisal wells and delineation wells may or may not be suspended for future use as development wells. During the Development Stage, production and injection wells are drilled as part of the original development plan designed by the engineers and geologists that make up the Asset Team for the reservoir. During the Plateau Stage, production and injection wells are drilled with the objective of keeping the surface facilities producing at 100 percent capacity. During the Decline Stage, infill production wells and pattern realignment wells are drilled to attempt to arrest the natural decline of the reservoir. Finally, during the Abandonment Stage, all wells are abandoned.
- Drilling engineers take the lead role in developing well proposals and rig schedules during all stages of the field development
- Drilling engineers take the lead role in any activity requiring a drilling rig. They are active members of any Asset Team during all phases of the life cycle of an oil or gas field. The drilling engineers reform all activities designing the well. They perform all calculations relating to the well design including: drilling fluid specifications, casing design (grades and depth), cement calculations, and drill string design
- Drilling engineers take an active role in coordinating all rig activities including: liaising with the drilling contractor, supply companies, government agencies, internal HSE (Health, Safety, and Environment Groups) and any other groups required for safe and efficient rig operations.
- Many companies and their personnel are involved in drilling oil and gas wells. These include:
- Drilling contractor company
- Operating company
- Service companies
- Cable tool rigs had their origins in the percussive drilling techniques used by ancient Chinese and Persian civilizations and are of historic importance because Colonel Edwin Drake used a cable tool rig to drill for oil in Titusville, PA in 1859. This event is considered to be the beginning of the modern oil and gas industry.
- Rotatory rigs are used almost exclusively in the oil and gas industry today. The two most common rotary drilling rigs are:
- Conventional rotary table rig
- Top-drive rig
- The conventional rotary table rig applies torque to the drill string and drill bit through a series of mechanical devices that sit on the rig floor. These are:
- Kelly
- Kelly bushing
- Master bushing
- Rotary table (or turn table)
- The rotary table is the device that is connected to the main power system of the rig (usually through a chain and gear system). The rotary table imparts the rotation (torque) to the master bushing, kelly bushing, kelly, drill string, and drill bit).
- The drill string is made up of 30-foot joints of drill pipe. These joints are connected as doubles (two joints) or triples (three joints) and racked and stored onto the side of the derrick as stands of drill pipe depending on the specifications of the rig.
- On a conventional rotary table rig, drill pipe is added to the drill string, one joint at a time. The next joint of drill pipe to be added to the drill string is temporarily stored in the mousehole on the rig floor.
- A top-drive rig applies torque to the drill string and drill bit with a motor mounted on the traveling block of the derrick.
- On a top-drive rig, a single joint, a double, or a triple of drill pipe can be added to the drill string during a connection. When multiple joints are connected, a significant reduction in the time required to connect drill pipe is achieved. This creates a more efficient drilling process.
- In this lesson, we also discussed three Mobile Offshore Drilling Units (or MODUs) used for offshore drilling:
- Jack-Up rigs
- Semi-Submersible rigs
- Drill ships
- A jack-up drilling rig is a rig with three or more (typically three) retractable legs that can be used to jack the rig up above the wave action of the water surface. Jack-up rigs are towed (or self-propelled) to the well’s surface location. Jack-up rigs can be used in water depths of up to 400 ft of water; can be used to drill wells to a Total Depth (TD) of 30,000 – 35,000 ft; and can be used to drill exploration, appraisal, delineation, or development wells.
- A semi-submersible drilling rig is a rig with multiple pontoons that are used to keep the rig floating while drilling. A semi-submersible rig uses a system of thrusters for dynamic positioning of the rig while drilling and is considered the most stable drilling rig for offshore drilling. Semi-submersible rigs can be used to drill wells in water depths up to 9,500 ft and are capable of drilling wells to a TD of 30,000 – 35,000 ft.
- A drill ship is a sea-going ship that is specifically modified to perform deep water drilling operations. Drill ships are used for deep water drilling in regions with little onshore logistical support. They can typically store large quantities of supplies which allows for their use in drilling exploration wells in more remote regions. In addition, drill ships can be used to drill appraisal, delineation, and development wells in oil or gas fields beneath deep water surface locations.
- In addition to the Mobile Offshore Drilling Units, we saw that offshore drilling can be performed off of large Production, Drilling, and Quarters Platforms.
8.6: Summary and Final Tasks
Summary
We began this lesson by discussing the life cycle of a producing field. The six stages of field development are:
- Exploration Stage
- Appraisal/Delineation Stage
- Development Stage
- Plateau Stage
- Decline Stage
- Abandonment Stage
We then discussed the role of the drilling engineer in each of these stages. The main point of this discussion was that whenever a drilling rig is involved in a field activity, a drilling engineer typically takes the primary role in developing the rig program (drilling fluid properties, cement properties, casing design, drill pipe specifications, etc.) and coordinating the rig activity with all required companies and agencies.
We then discussed the role of the drilling contract company in the oil and gas industry. We discussed two common contracts used by operating companies to obtain the services of a drilling company, its equipment (including the rig), and its personnel:
- Day-rate contract (most common contract)
- Turn key contract
We then discussed the various members of the rig crew, their roles and responsibilities, whom they report to, the company that employed them (operating company, drilling company, or service company). Later in the lesson, we saw several YouTube videos showing the rig crew personnel performing some of their duties.
We also discussed historic rigs (cable tool rigs) and modern rigs (rotary rigs). The two rotary rigs that we discussed in detail were the conventional rotary table rig and the top-drive rig. The conventional rotary rig has been the work-horse of the industry for most of the 20th century, but the top-drive rig, a relatively recent innovation, is fast becoming the industry standard.
The two major advantages of a top-drive drilling rig are:
- The ability to handle multiple joints (two or three joints) of drill pipe at one time during connecting/unconnenting operations
- The ability to rotate the drill pipe while tripping into or out of the wellbore to avoid Stuck Pipe during tripping operations
Finally, we discussed the mobile and fixed drilling in offshore environments. In particular, we discussed:
- Mobile Offshore Drilling Units (MODUs):
- Jack-up rigs
- Semi-submersible rigs
- Drill ships
- Fixed drilling centers on large Production, Drilling, and Quarters (PDQ) Platforms
Final Tasks
Complete all of the Lesson 8 tasks!
You have reached the end of Lesson 8! Double-check the to-do list on the Lesson 8 Overview page [112] to make sure you have completed all of the activities listed there before you begin Lesson 9.
Lesson 9: Drilling Engineering: Drilling Rig Systems and the Drilling Process
9.0: Lesson Overview
In this lesson, we will continue discussing the drilling of oil and gas wells. In particular, we will discusst the major systems and sub-systems of modern rotary drilling rigs including their roles in the drilling process.
Learning Objectives
By the end of this lesson, you should be able to:
- describe and discuss the five major systems of a drilling rig:
- the Power System,
- the Hoisting System,
- the Circulation System,
- the Rotary System, and
- the Well Control System (Blowout Prevention System);
- discuss the role of these systems in the drilling of oil and gas wells;
- list the sub-systems that comprise these five major systems;
- describe the important sub-systems on the drilling rig;
- discuss the drilling process and how rig activities and systems interact during this process
Lesson 9 Checklist
| To Read | Read the Lesson 9 online material | Click the Introduction link below to continue reading the Lesson 9 material |
|---|---|---|
| To Do | Lesson 9 Quiz | Take the Lesson 9 Quiz in Canvas |
Please refer to the Calendar in Canvas for specific time frames and due dates.
Questions?
If you have questions, please feel free to post them to the Course Q&A Discussion Board in Canvas. While you are there, feel free to post your own responses if you, too, are able to help a classmate.
9.1: Introduction
In the last lesson, we learned about Rig Contracts, the Rig Crew, and Different Drilling Rigs. In this lesson, we will continue our discussions of the drilling rig and start a discussion on the drilling process. In Lesson 8, we saw that there are different onshore and offshore drilling rigs. While these rigs have different applications and there are pros and cons for each, there are many similarities. We will continue our discussion on drilling rigs with these similarities.
9.2: Major Systems on a Drilling Rig
While there are different types of drilling rigs, these rigs obviously share many similarities since the tasks that they perform are identical. In particular, all modern hydrocarbon rotary rigs contain five main systems. These systems are:
- the Power System
- the Hoisting System
- the Rotary System
- the Circulation System
- the Well Control System (Blowout Prevention System)
These systems are shown in Figure 9.01. In addition, Figure 9.02 shows a more detailed schematic diagram of a rotary table, land rig.

 |
||
|
|
|
| Source: Serintel: Oil and Gas Portal - Drilling Technologies [113] | ||
9.2.1: The Power System
The power system on a drilling rig provides the power for the other main systems on the rig and other ancillary systems, such as electrical systems, pumps, etc. The system typically consists of a prime mover (the component of the power system that generates the raw power) and a means to transmit the raw power to the end-use components on the rig.
In the detailed rig schematic (Figure 9.02a), the power system is comprised of:
- the Fuel Storage (Item 37)
- the Engines and Generators (Item 38)

Historically, coal was used to generate the power for drilling rigs; however, modern drilling rigs use other sources of fuel. Typically, modern rigs are now run using an internal combustion engine with diesel or lease fuel. Diesel oil is a petroleum-based fuel that is a product of the distillation process. If the rig is running in a developed field, then the field may have a small on-site refinery that is used to distill the diesel fuel. If the rig is drilling an exploration, appraisal, or delineation well, then the fuel will need to be delivered from an external source and stored on-site.
Lease fuel is typically produced natural gas. As we have learned, natural gas is always produced along with crude oil. Again, if the rig is drilling wells in a developed field, then the field may use the natural gas or Natural Gas Liquids (NGL) to fuel the prime mover. This natural gas may be processed to remove NGLs if a gas plant is available on site; may need to burn these hydrocarbon liquids (possible sales product) if a gas plant is unavailable; or may burn the processed NGLs (butane).
The transmission of the power can be:
- mechanical
- direct current (DC) electrical generator
- alternating current (AC) electrical generator with silicon-controlled rectifier (SCR) to direct current (DC)
In the mechanical transmission, power is generated with the prime mover and is transmitted to the end-use components by the application of chains and sprockets (similar to a bicycle), drive belts, drive shafts, etc. In a direct current (DC) electrical system, an internal combustion engine operates an electrical generator (in this case a DC generator) and the electrical energy is transmitted to the motors, electrical actuators, etc. Finally, in an alternating current (AC) electrical system, an internal combustion engine operates an electrical generator (in this case an AC generator) which is converted to DC with a silicon-controlled rectifier (SCR). AC-SCR power systems are the most widely used power systems on modern drilling rigs.
9.2.2: The Hoisting System
The hoisting system on a drilling rig does the heavy lifting on the rig. It is used to raise, lower, and suspend the drill string and lift casing and tubing for installation into the well.
In the detailed rig schematic (Figure 9.02b) the hoisting system is comprised of:
- the Crown Block (Item 1)
- the Mast/Derrick (Item 2)
- the Monkey Board (Item 3)
- the Traveling Block (Item 4)
- the Hook (Item 5)
- the Swivel (Item 6)
- the Drawworks (Item 13)
- the Weight Indicator (Item 14)
- the Drilling Line (Item 39)

A schematic of the hoisting system is shown in Figure 9.03 for a kelly drive rig. In this figure, the derrick (or mast) provides the structural support for the hoist system. It must be capable of supporting the entire load on the system including the weight of the drill string (accounting for buoyancy effects) and any frictional forces.
The crown block and the traveling block form a Block and Tackle System on the rig. The drill line can be strung as pairs of 2 through 12 lines (six pairs). The greater the number of lines (and pulleys) in the block and tackle system, the greater its lifting power but at the expense of slower upward and downward movement of the system.

The drawworks of the hoisting system is a winch that reels the drilling line in or out causing the traveling block to move up or down. The drawworks is the component of the hoisting system that consumes energy from the power system. The drum on the drawworks is grooved to accommodate a specific size drilling line. Figure 9.04 shows a photo of an actual drawworks used on a drilling rig .
Not shown on the schematic or the photo is the braking system on the drawworks. Modern rigs use both a mechanical brake and an electromagnetic brake. The braking system is an integral part of the drilling process because it is used to control the Weight-on-Bit (WOB) during drilling. The two most important drilling parameters within the Driller‘s control to maximize the Rate of Penetration (ROP) are the weight-on-bit and the rotational speed of the rotary system in Revolutions per Minute (RPM).
The weight-on-bit is achieved with the weight of the drill pipe and Drill Collars, however the optimum weight-on-bit is often less than the total weight of the drill string. The brake is used to take up some of the weight of the drill string, so that the weight-on-bit is only a fraction of the total weight.

Also shown in Figure 9.03 is the Swivel. The swivel is the link that connects the hoisting system to the rotary system and to the circulation system. The function of the swivel is to:
- hold the weight of the drill string on the hoisting system (the hoisting system does not rotate);
- allow rotation of the drill string below it (the drill string, Bottom-Hole Assembly (BHA), and drill bit all rotate);
- allow passage of the drilling fluid from the circulation system (non-rotating) to the drill string, Bottom-Hole Assembly (BHA), and drill bit of the rotary system.
9.2.3: The Circulation System
The circulation system on the rig is the system that allows for circulation of the Drilling Fluid or Mud down through the hollow drill string and up through the annular space between the drill string and wellbore. It is a continuous system of pumps, distribution lines, storage tanks, storage pits, and cleansing units that allows the drilling fluid to fulfill its primary objectives (these will be discussed later in this lesson). The mud pumps of the circulation system and the drawworks of the hoisting systems are the two largest draws on the power from the power system
In the detailed rig schematic (Figure 9.02c), the circulation system is comprised of:
- the Swivel (Item 6)
- the Rotary Hose (Item 17)
- the Mud Return Line (Item 23)
- the Shale Shaker (Item 24)
- the Choke Manifold (Item 25)
- the Mud Gas Separator (Item 26)
- the Degasser (Item 27)
- the Reserve Pit (Item 28)
- the Mud Pits (Item 29)
- the Desander (Item 30)
- the Desilter (Item 31)
- the Mud Pumps (Item 32)
- the Mud Discharge Line (Item 33)
- the Bulk Mud Components Storage (Item 34)
- the Mud House (Item 35)
- the Water Tank (Item 36)

Drilling fluid is mixed in the mud pits and pumped by the mud pumps through the swivel, through the blow out preventer (not part of the circulation system) down the hollow drill pipe, through holes (Jet Nozzles) in the bit, up the annular space between drill pipe and wellbore (where it lifts the rock cuttings), to the surface, through the Solids Control Equipment (Shale Shaker, Desander, and Desilter), and back to the mud pits. A schematic of the circulation system is shown in Figure 9.05.
In this figure, fresh water-based drilling fluid (mud) is mixed with water from the Water Tank (not shown in Figure 9.05) and components from the Bulk Mud Components Storage (not shown in Figure 9.05) in the Mud Pit. The Mud Pumps then pump the mud through the swivel, kelly, kelly bushing, and rotary table down to the drill string.
The mud pumps on a typical drilling rig are either single-action or double-action Reciprocating (Positive Displacement) Pumps which may contain two pistons-cylinders (duplex pump) or three pistons-cylinders (triplex pump). Figure 9.06 shows schematics of a single piston-cylinder in (A) a single-action and (B) a double-action reciprocating pump.
In these pumps, the positive pressure and negative pressure (suction) in the cylinder cause the valves to open and close (note: the valves in the schematic are simple representations of the actual valves). Due to the high viscosity of the drilling fluid, the inlet side of the pump may require a Charge Pump to keep fluids moving into the cylinders at high pressures and to prevent Cavitation in the pump.


From the mud pumps, the drilling fluid goes to the swivel, through the blow out preventer, and down the hollow drill string and bottom-hole assembly. The drilling fluid then goes through jet nozzles in the drill bit; at which point, it begins its return to the surface. The drilling fluid travels up the annular space between the drill pipe and the wellbore, picking up and carrying the drill cuttings up the hole.
Once the drilling fluid reaches the surface, it goes through the mud return line to the gas-mud separator and the solids control equipment. The shale shaker is where the large cuttings from the returning drilling fluid are removed. The shale shaker is a set of vibrating mesh screens that allow the mud to pass through while filtering out cuttings of different size at screen screen mesh sizes. A Mudlogger or a Well-Site Geologist may be stationed at the shale shaker to analyze the cuttings to determine the lithology of the rock and the depth within the Stratigraphic Column at which the well is currently being drilled.
The drilling fluid then passes through the Desander and Desilter. These are hydrocyclones which use centrifugal forces to separate the smaller solids from the drilling fluid. The desander typically removes solids with a diameter in the range of 45 – 74 μm, while the desilter removes solids with a diameter in the range of 15 – 44 μm.
The drilling fluid is then sent through a degasser to remove any gas bubbles that have been picked up during the circulation. These gasses may include natural gas from the subsurface or air acquired during the solids control. Typically, the degasser is a piece of equipment that subjects the drilling fluid to slight vacuum to cause the gas to expand for extraction. The drilling fluid is then returned to the mud pit to start the circulation process over again.
We have discussed the mechanics of how the drilling fluid is circulated during the drilling process, but we have not discussed the role of the drilling fluid. The term “mud” is often used in oil and gas well drilling because historically the most common water-based drilling fluids were mixtures of water and finely ground, bentonite clays which, in fact, are muds.
There are many objectives for using a drilling fluid. These include:
- lift drill cuttings from the bottom of the wellbore to the surface;
- suspend cuttings to prevent them from falling downhole if circulation is temporarily ceased;
- release the cuttings when they are brought to the surface;
- stabilize the borehole during drilling operations (exert hydrostatic or hydrodynamic pressure on the borehole to prevent rock caving into the wellbore);
- control formation pore pressures to assure desired well control (apply hydrostatic and hydrodynamic pressures in excess of the formation pore pressures to prevent fluids from entering the wellbore);
- deposit an impermeable filter cake onto the wellbore walls to further prevent fluids from permeable formations from entering the wellbore;
- minimize reservoir damage (assure low skin values) when drilling through the reservoir section of the well;
- cool the drill bit during drilling operations;
- lubricate the drill bit during drilling operations;
- allow for pressure signals from Logging While Drilling (LWD) or Measurement While Drilling (MWD) tools to be transmitted to the surface (LWD and MWD data are transmitted to the surface using pressure pulses in the drilling fluid);
- allow for pressure signals to be sent to the bottom of the well to pressure actuate certain downhole equipment;
- minimize environmental impact on subsurface natural aquifers.
As I stated earlier, historically drilling fluids were mixtures of bentonite clay, water, and certain additives to manipulate the properties of the mud (density, viscosity, fluid loss properties, gelling qualities, etc.). Today, there are several different options available for drilling fluids. These include:
- water-based muds (WBM)
- oil-based muds (OBM)
- foams
- air
Of the listed drilling fluids, the water-based muds and the oil-based muds are the most common; foam drilling and air drilling can only be used under specialized conditions. Of the two liquid based mud systems (water-based muds and oil-based muds), water-based muds are the most common mud system. They are more environmentally friendly and are used almost exclusively to drill the shallow portions of the well where fresh water aquifers exist to minimize any contamination to those aquifers. As this implies, drilling fluids can be – and often are – switched during the course of drilling operations in single well.
In addition, water-based muds are cheaper than oil-based muds, so they are used to reduce drilling costs and commonly represent the “default” selection for a drilling fluid. In other words, water-based muds are often used unless there is a specific reason to switch to an oil-based mud.
Oil-based muds are formulated with diesel oil, mineral oil, or synthetic oils as a continuous phase and water as a dispersed phase in an emulsion. In addition, additives such as emulsifiers and gelling agents are also used. They were specifically developed to address certain drilling problems encountered with water-based muds. The reasons for using an oil-based mud include:
- drilling through shales that are susceptible to swelling (in particular, highly smectite-rich shales). Shales contain a large amount of clay material and when these clays come in contact with the water in a water-based mud system, the clays may swell causing the shales to collapse into the hole. Smectite-rich shale formations are often referred to as “Gumbo” or “Gumbo Clays” in the drilling industry;
- reducing torque and drag problems in deviated wells. Since oil, a lubricant, is the continuous phase in the mud system, the torque and drag between the drill pipe and the wellbore is reduced with oil-based muds;
- achieving greater thermal stability at greater depths. Oil-based muds have been found to retain their stability (retain their desired properties) at greater down hole temperatures;
- achieving greater resistance to chemical contamination. Many substances found down-hole (salt, CO2, H2S, etc.) are soluble in water. The introduction of these substances into the water-based mud system may have a deleterious impact on different mud properties (density, viscosity, fluid loss properties, gelling properties, etc.). These substances are not soluble in oil and, therefore, have will not impact oil-based mud properties.
The first three bullet points in this list are becoming more common problems in the oil and gas industry. The shale boom in the U.S. has made long horizontal sections in shale reservoirs targets for drilling. In addition, deviated wells and deeper wells are also becoming more common. For these reasons, the use of oil-based muds is also becoming more common.
There are also several disadvantages with oil-based muds. These include:
- high initial costs. Often in an active drilling campaign, if certain depth intervals require an oil-based mud, the mud is stored and reused in different wells;
- slow rates of penetration. Historically, the rate of penetration has been statistically slower for oil-based muds than it is for water-based muds. The rate of penetration is the speed at which the drilling process progresses (depth versus time) and is a function of many factors other than mud type, including: weight on bit, RPM, lithologies being drilled through, bit type, bit wear, etc.;
- environmental concerns:
- oil contamination of subsurface fresh water aquifers,
- cleaning and disposal of oil contaminated rock cuttings;
- kick detection. If gas enters the wellbore (a Kick), it may go into solution in the oil in deeper, higher pressure sections of the well and come out of solution closer to the surface;
- formation evaluation. Some readings from well logs or core analysis may be sensitive to oil entering the formation of interest (for example, if oil from the oil-based mud enters the reservoir in the near-well vicinity, then tools used to detect oil saturation may read artificially high).
Other drilling fluids currently in use that were listed earlier are foams and air. In the context of drilling fluids, foams have the consistency of shaving cream. Both foam and air drilling are used in hard rock regions, such as in the Rocky Mountains, where drill bits render the drill cuttings to dust. Thus, the foam or air only needs to lift this dust to the surface. Air drilling is always an environmentally friendly option if it is applicable because environmental contamination by air is never an issue.
9.2.4: The Rotary System
The rotary system on a drilling rig is the system that causes the drill bit rotate at the bottom of wellbore. We have discussed some components of the rotary system when we discussed rotary table and top-drive rigs, but we have not yet discussed the entire system.
In the detailed rig schematic (Figure 9.02d), the rotary system is comprised of:
- the Swivel (Item 6)
- the Kelly (Item 8) – the functionality on a top-drive rig is handled by the top-drive
- the Kelly Bushing (Item 9) – the functionality on a top-drive rig is handled by the top-drive
- the Master Bushing (Item 10) – the functionality on a top-drive rig is handled by the top-drive
- the Rotary Table (not shown in Figure 9.02d) – the functionality on a top-drive rig is handled by the top-drive
- the Mousehole (Item 11) – used to connect single joints on a top-drive or rotary table rig
- the Rat Hole (Item 12)
- the Rotary Hose (Item 17)
- the Drill String (not shown in Figure 9.02d)
- the Bottom-Hole Assembly (not shown in Figure 9.02d)
- the Drill Bit (not shown in Figure 9.02d)

A schematic of the rotary system is shown in Figure 9.07. As we can see in Figure 9.07, the rotary system shares many components with the circulation system. This is because in the rotary system, these components rotate in support of causing the bit to rotate, while in the circulation system, these components act as conduits for the drilling fluid.

In Lesson 8, we saw that the rotary table imparted the torque for the drill string in a conventional rotary table rig, while the top-drive imparted this torque on a top-drive rig. We also saw that drill pipe was added to the drill string one joint at a time on a rotatory table rig, while a top-drive could add multiple joints of drill pipe during one connection operation.
The Bottom-Hole Assembly is comprised of any bottom hole equipment required to drill the current section of the well. A bottom-hole assembly may be as simple as a Drilling Collar. Drill collars are sections of heavy, thick walled pipe used to add weight-on-bit to the drill string. More complicated bottom-hole assemblies may include Jars, downhole directional steering and positioning equipment, logging-while-drilling, and measure-while-drilling equipment.
Jars are mechanical devices that deliver a transfer of kinetic energy to another piece of downhole equipment as the result of an impact. They are typically used to loosen a piece of downhole equipment with an impact (jarring action). You can think of a jar as comparable to a hammer used to loosen two boards that are nailed together by hitting one of the boards in the direction opposite of the head of the nail.
At the end of the drill string and bottom-hole assembly is the drill bit. There are many types of drill bits, but we will focus on two types of drilling bits, the Tri-Cone (or Roller Cone) Bit and Fixed-Cutter Bit. In addition, we will be discussing two variants of the tri-cone bit: the milled-tooth bit and the insert bit. All of these bits can be classified as in the following bullet list:
- tri-cone bits
- milled-tooth bits
- insert bits
- fixed-cutter bits
Tri-cone bits are the most common drilling bits and, historically, have been the workhorse of the drilling industry. As the name implies, tri-cone bits contain three cones, each of which contain cutting teeth.
The two-cone bit (an early version of the tri-cone bit) was invented by Howard Hughes Jr.’s father (Howard Sr.). The tri-cone bit and the formation of the Hughes Tool Co. (now part of Baker-Hughes, a subsidiary of the General Electric Corporation) was the source of the Hughes family wealth. In case you do not know who Howard Hughes Jr. was, he was an award winning pilot in the 1920s and 1930s (holder of several aerial speed records and subject of the movie “The Aviator”), a filmmaker (had controlling interest of RKO Studios and actively produced several notable silent and early “talkie” films), airplane designer (owner of Hughes Aircraft – contractor for the world’s largest wooden airplane, “The Spruce Goose,” with Howard as its only pilot in 1947), and a billionaire by the 1970s and 1980s (back when a billion dollars had some value).
In a milled-tooth bit, the teeth of the bit are machine-milled along with the rest of the cone. The cones of the tri-cone bit, including the teeth, are formed from a single, solid piece of steel. An example of a milled-tooth bit is shown in Figure 9.08.

In this figure, we can see that the teeth of the bit are intrinsic parts of the cones; they are milled from the same piece of steel. These bits, as do all tri-cone bits, drill through the rock by exerting the full weight-on-bit on only a few contact points (the sharpened teeth) between the bit and the rock. This exerts extremely high levels of stress at the contact points causing the rock to fail catastrophically (almost explosively). We will see this in a YouTube video later in the lesson.
One design feature of the tri-cone bit is the interaction of the teeth on the different cones helping to remove any small cuttings or sticky shales/clays (Gumbo Shales) that may get lodged between the teeth and reduce the efficiency of the bit. This phenomenon of cuttings and clays getting lodged between bit teeth is referred to as Bit Balling and results in slower Rates-of-Penetration (ROP) of the drilling process. The self-cleaning action of the teeth in a tri-cone bit is designed to reduce the bit balling.
Milled-tooth tri-cone bits are mainly used for drilling through soft rock formations. This is because, no matter how strong the steel used in the construction of the cone, hard rock can cause excessive wear and degradation of the teeth.
Insert drill bits, on the other hand, are bits in which the teeth are made from materials stronger than the steel used in the cone and are inserted into cone. Example of insert tri-cone bits are shown in Figure 9.09.

While the insert bit shown in Figure 9.09 may superficially look like the milled-tooth bit; careful inspection reveals that the teeth in the insert bit are not milled but are inserted into the cone. Typically, the teeth in an insert bit are made from tungsten-carbide steel (Tungsten Carbide Insert bit or TCI bit) which is a much stronger alloy of steel than the alloys used for the cones. Other design features included on insert bits include the length and the shape of the teeth (short, round-shaped teeth for hard rock formations or long, chisel-shaped teeth soft formations). These designs allow for a range of lithologies for these bits to be used: in hard rock formations that would be inappropriate for milled-tooth bits or in soft rock formations for extended bit-life.
While the insert bit helps to alleviate the issues with tooth-wear, there is an additional source of wear that can shorten the life of a drilling bit. Due to the moving parts associated with a tri-cone (or roller) bit, the bit requires a bearing where the moving parts meet and move past one another. Thus, the wear on the bearings may also shorten the life of the bit.
Fixed cutter bits are bits that do not contain any moving parts. These bits are designed to drill by shearing and scraping the rock formations as opposed to the gouging action used by a tri-cone bit. These bits typically use industrially made diamonds for the teeth and are also known as Polycrystalline Diamond Compact (PDC) bits. Figure 9.10 shows an example of a PDC bit.

The PDC bits are used to drill through very hard rock formations or for extended bit-life drilling. These bits have a large initial cost but because of the hard teeth and lack of any moving parts have a longer bit-life. One recent innovation for PDC bits in geologic basins with many shallow (short-footage) drill sites is the ability to rent the drill bit from the drilling company rather than to purchase it from a tool company. This innovation allows for an operating company to rent the bit and to use it for the footage that they require before relinquishing it to another operating company.
We have discussed that the tri-cone bits and the fixed cutter bits have different drilling actions. Here is a YouTube video, "Drill Bits - Oil and Gas Drilling: From Planning to Production" (3:26), that demonstrates the differences of the explosive, gouging, and crushing action of the tri-cone bit and the scraping action of the fixed cutter bits:
9.2.5: The Well Control System (Blowout Prevention System)
The Well Control System or the Blowout Prevention System on a drilling rig is the system that prevents the uncontrolled, catastrophic release of high-pressure fluids (oil, gas, or salt water) from subsurface formations. These uncontrolled releases of formation fluids are referred to as Blowouts. Due to the explosive nature of oil and gas, any spark on the surface can result in the ignition of the fluids and an explosion on the rig. An explosive blowout and the failure of the Well Control System were the causes of the Mocondo Well disaster that killed eleven of the rig crew on the Deep Water Horizon Rig on April 20, 2010 and resulted in 35,000 to 60,000 bbl/day of crude oil to spill into the Gulf of Mexico. We will discuss this later in the lesson.
In the detailed rig schematic (Figure 9.02e), the well control system is comprised of:
- the Accumulator (Item 18)
- the Blowout Preventer (not shown in Figure 9.02e)

A picture of a Blowout Preventer (BOP), pronounced “B-O-P” not “bop”, is shown in Figure 9.11.

The blowout preventers are the principal piece of equipment in the well control system and are operated hydraulically; pressurized fluids are used to operate pistons and cylinders to open or close the valves on the BOP. The Accumulators (Item 18 in Figure 9.02) are used to store pressurized, non-explosive gas and pressurized hydraulic fluid to run the hydraulics systems on the rig. The accumulators store enough compressed energy to operate the blowout preventers even if the Power System of the rig is not operating.
The blowout preventer is a large system of valves each of which is capable of isolating the subsurface of the well from the rig to provide control over the well. These valves are typically stacked as shown in the Figure 9.11 and sit below the rig floor on land wells or some offshore wells; or they may sit on the seabed on other offshore wells.
A schematic diagram of a blowout preventer is shown in Figure 9.12.
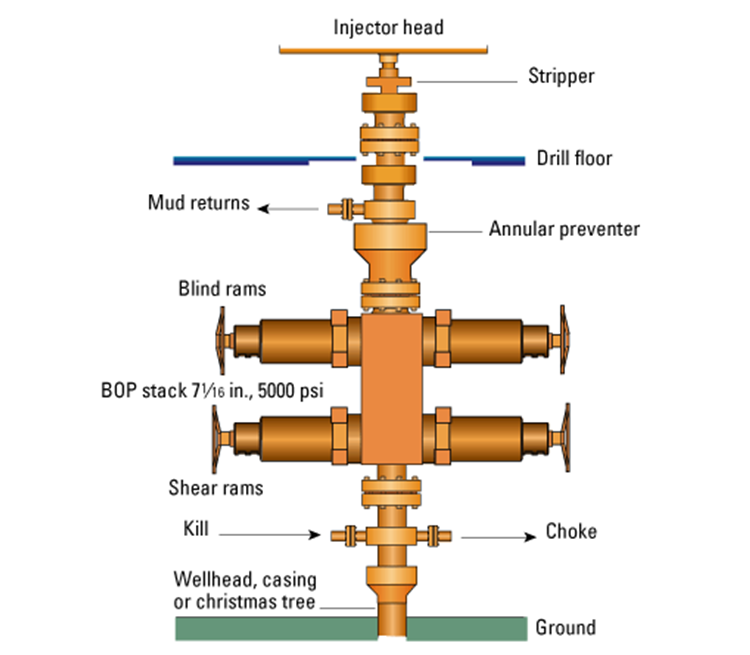
Figure 9.12 shows three type of valves (there are others) – an Annular Preventer, Blind Rams, and Shear Rams. The Annular preventer is the ring-shaped piece of equipment on the top of the BOP in Figure 9.11. As the name implies, the annular preventer is used to prevent flow through the annular space between the drill string or casing and the annular preventer. The annular preventer can also be used for non-cylindrical pipe, such as the kelly, or open hole. The annular preventer consists of a doughnut shaped bladder that when in the open position allows the drill pipe to rotate but in the closed position seals the annulus. Figure 9.13 provides a schematic of the annular preventer.
In Figure 9.13, the blue area represents the doughnut-shaped bladder. As mentioned earlier, in the open position, (A), the drill pipe can be rotated or can be run up or down; while in the closed position, (B), the bladder pushes out, closing off the drill pipe, kelly, or open hole. The bladder based sealing element is not as effective as the ram type sealing elements; however, almost all blowout preventer stacks include at least one annular preventer.
Schematics of the ram-type preventers: the blind rams, the shear rams, and the pipe rams (pipe rams are not shown in Figure 9.12) are shown in Figure 9.14.

This figure shows that:
- blind rams isolate both the pipe and the annular space by crushing the pipe and it pinching-off when closed;
- shear rams isolate both the pipe and the annular space by shearing-off the pipe when closed;
- blind shear rams isolate both the pipe and the annular space by shearing-off and crushing the pipe when closed;
- pipe rams isolate the annular space by wrapping around the pipe when closed.
A blowout begins as a Kick (entry of subsurface formation fluids into the wellbore). What distinguishes a kick from a blowout is that a kick can be controlled while a blowout is uncontrollable. We have already discussed two of the defenses against kicks when we discussed drilling fluids when we listed the objectives of the drilling fluid:
- control formation pore pressures to assure desired well control (apply hydrostatic and hydrodynamic pressures in excess of the formation pore pressures to prevent fluids from entering the wellbore);
- deposit an impermeable filter cake onto the wellbore walls to further prevent fluids from permeable formations from entering the wellbore.
In the first objective re-quoted above, if we can keep the pressure exerted by the drilling mud greater than the pore pressure, then we know that fluids will flow in the direction of the mud to the formation. This cannot always be achieved. For example, if we drill through a natural fracture or if our mud density is too great and we inadvertently fracture one formation, then we may lose large quantities of the drilling fluid into the fracture (Lost Circulation). In this situation, instead of having the full weight of the mud column exerting pressure on a second (porous and permeable) formation, we may only have a fraction of the oil column height exerting a lower pressure on that second formation.
In the second objective re-quoted above, if we deposit an impermeable Drill Cake (filter cake) across an otherwise porous and permeable formation, then for a slightly Underbalanced Pressure (drilling fluid pressure lower than the formation pressure) we have created a seal between the wellbore and the formation. Again, this is not a Failsafe System because at greater underbalanced pressures, the higher formation pressures may be able to displace the drill cake.
The two previously discussed methods are used to help prevent a kick from occurring, but as mentioned they are not always successful, and kicks may still occur. The causes of a kick include:
- insufficient mud weight (density): the hydrostatic pressure exerted by the mud column is not greater than the formation pore pressure;
- improper mud replacement during tripping: while tripping out of the hole mud volumes must be pumped into the wellbore at high enough rates to replace drill pipe being removed from the wellbore;
- swabbing: removing drill pipe from the wellbore can create a negative pressure (suction) if the drill pipe is removed too quickly;
- cut mud: if gas is entering the wellbore, then it may effectively reduce the wellbore pressure gradient;
- lost circulation: as discussed earlier if large volumes of drilling fluid enter the subsurface in (1) high permeability formations, natural fractures, or drilling-induced fractures, then the effect is a shortened height and weight of the mud column.
The following are Indicators/Warning Signs of a kick:
- increase in the rate of flow of the drilling fluid returns at constant pump rates (primary indicator of a kick): The increased rate is caused by formation fluids entering the wellbore and is a strong indication of a kick. In addition, if it is a gas kick, due to the compressible nature of gas, as the gas bubble travels up-hole and hydrostatic pressures decrease, the volume of the bubble will increase due to expansion.
- volume of mud in the mud pit increases when no additional drilling fluids are added to the mud system (primary indicator of a kick): For the same reasons as mentioned above, if the volume of mud in the mud pits increases when no additional fluids have intentionally added, then the increased volume is caused by formation fluids entering the wellbore and is a strong indication of a kick.
- drilling fluids returns continue to flow when the mud pumps are turned off (primary indicator of a kick): Drilling fluid returns when the mud pumps are shut-off indicate that formation fluids are entering the wellbore and displacing the mud.
- improper wellbore fill-up/volume-balance on trips (primary indicator of a kick): If the drill pipe is removed from the wellbore, then the change in volume in the mud pits should equal the volume of the drill pipe removed from the hole. An improper volume balance is a strong indicator of a kick.
- pump pressure decrease and pump stroke increase (secondary indicator of a kick): If low density fluids are displacing heavier drilling fluid in the annulus, then this will cause the pump pressure to decrease (the annular side of the u-tube is lighter than the drill pipe side of the u-tube which contains the mud pump pressure gauge). The imbalance in the u-tube, just described, will cause the heavier drilling fluid in the drill pipe to fall due to gravity, causing the mud pump to increase the number of strokes to keep up with the pressure imbalance.
- change in the apparent weight-on-bit (secondary indicator of a kick): If the weight-on-bit indicator in the rig’s Dog House shows a change in the weight-on-bit that is not explainable by the current drilling operations, then this may be an indication of a kick. The apparent weight-on-bit is affected by the buoyance caused by the wellbore fluid, which in turn, is affected by the density of the wellbore fluid. If a lighter formation fluid begins to replace the heavier, more dense drilling fluid, then an apparent increase in the weight-on-bit will occur.
- occurrence of a Drill Break or Bit Drop (secondary indicator of a kick): A Drill Break (sudden change in the rate-of-penetration) or Bit Drop (sudden increase in the drill bit depth) typically occur at a change in the lithology of the formation being drilled. In particular, a large bit drop may be an indication of drilling through a natural facture system. Both drill breaks and bit drops are normally recorded in the drilling records. When working on naturally fracture reservoirs, these drilling records may be useful for mapping natural fractures. I personally worked in a field where we had a 12 meter (~ 36 ft) bit drop in one well in the reservoir – think about it, you are drilling away at a certain rate-of-penetration and, all of a sudden, the bit drops 36 feet for no apparent reason. This was caused by drilling through a solution enhanced fracture which over geologic time formed a cavern in the reservoir (this occurred several years prior to my arrival, but it was in the drilling records).
- reduction in the mud weight (secondary indicator of a kick): The Mud Man may observe a reduction or Cut in the mud density at the rig-site mud laboratory. This again may be an indication of a kick.
When a kick occurs, the Operating Company and Drilling Company always have well-specific plans in-place for all wells to ensure that any controllable kick does not turn into an uncontrollable blowout. I cannot go into the details of a well-specific procedures, but they will include some of the following features if a kick occurs during drilling operations:
- Stop drill pipe rotation.
- Pick the drill bit off-bottom and Space Out (Spacing out refers to pulling the drill pipe out the hole so that the top connection – the thickest part of the drill string containing the threads and joints – is several feet above the rig floor. Spacing out ensures that the smaller diameter section of the drill string is inside the BOP, so that pipe rams can close and seat properly or blind rams or shear rams are opposite the smallest diameter section of steel. See Figure 9.15B)
- Stop the mud pumps and check for continued Mud Returns (flow of mud from the well).
- If mud returns continue:
- Shut-in the well with the annular preventer or pipe rams:
- Hard shut-in (choke in Figure 9.12 is closed)
- Soft shut-in (choke in Figure 9.12 is opened)
- If a hard shut-in was used, open the choke
- Weight Up (add the mud weighting additives) to the desired density – this is the Kill Fluid used to Kill the Well
- Circulate the kill fluid through the kill line, down the wellbore, and out of the choke (see Figure 9.12) using an industry standard method:
- The Driller’s Method
- The Weight and Wait Method
- Shut-in the well with the annular preventer or pipe rams:
Other procedures will be used if the kick occurs while tripping into or out of the well. The details of some aspects of this procedure such as hard or soft shut-ins and the circulation methods, The Driller’s Method and The Weight and Wait Method, will be discussed in detail in your later drilling classes. More importantly, for every well that you are involved with, there will always be Daily Safety Meetings that discuss the current status of the well and the important safety aspects of all drilling activities related to that day’s operations.
So, we have discussed the role of drilling fluid to exert pressure on porous and permeable formations and to coat them with an impermeable filter cake to help prevent kicks from occurring. We have also discussed the role of the blowout preventer and company procedures to control a kick once one occurs. So, how do blowouts happen?
Perhaps you remember the Macondo Blowout (Deep Water Horizon Rig) disaster. The name Macondo was the Prospect name (remember, we discussed prospects and well proposals in a previous lesson) while the Deep Water Horizon was the name of the rig. This was the largest oil spill in the Gulf of Mexico. When the disaster occurred, eleven members of the rig crew were killed by the explosion when the natural gas ignited.

The following YouTube video, "Deepwater Horizon Blowout Animation" (11:22), describes the Deep Water Horizon disaster and what its root causes were:
After learning about offshore drilling rigs, drilling crews, components of the drilling rig, kicks, and blowouts, I would highly recommend watching the movie “Deep Water Horizon” and use your knowledge about oil and gas well drilling to identify some of the technical aspects of the film. Ask yourselves some technical questions:
- What type of offshore drilling rig was the Deep Water Horizon?
- What type of well was being drilled (exploration, appraisal/delineation, or development well)?
- What part of the rig crew were the main characters (both the “good guys” and the “bad guys”)?
- What companies (operating companies, drilling companies, or service companies) did these characters work for?
- What were the root causes of the disaster?
- Why were running Cement Bond Logs (CBL) – well logs showing the quality of the cement job –and pressure-testing the cement so important to averting this disaster?
- What is “real” and what is “Hollywood”?
9.3: The Drilling Process
We have discussed the components of the drilling rig, now let’s discuss the drilling process itself. An oil or gas well is drilled in a very ordered sequence. The steps in this sequence are almost universally applied to the drilling of all wells.
- Plan the Well: As we have discussed, exploration well prospects are generated by exploration geologists; while development wells locations and objectives are generated by development geologists. Once the surface locations and well objectives are known, the geologists work with the drilling engineers to develop the detail drilling proposals. In addition, all permits (environmental, safety, regulatory, etc.) are acquired during the final stages of the planning process when a solid well proposal is developed.
- Perform Shallow Gas Survey: To ensure there are no shallow gas hazards which may result in a kick or blow out, a shallow gas survey is performed to identify the locations and depths of any potential shallow gas hazards. Preliminary surface locations and well trajectories may be altered from the original well proposal to avoid these shallow gas hazards.
- Prepare the Wellsite: The site preparation involves building clearing land for use by the rig, building access roads to the well site or well pad, construct infrastructure for water, water disposal, and electricity, dig and line all mud pits to prevent ground water or water table contamination, dig reserve pits for cutting storage (for eventual disposal), and drill the holes which will eventually become the rat hole and the mousehole. The site preparation may involve multiple contractors and companies to perform all of the required work. As we discussed in earlier lessons, a lot of site-preparation time and the environmental footprint can be minimized if multi-well pads are used in the field development.
- Set the Conductor Casing: Prior to the arrival of the drilling rig, an Auger Unit (in hard rock regions) will drill a large diameter hole capable of accommodating 18 in. to 36 in. conductor casing (see Figure 9.16). In soft rock regions or at offshore locations, a diesel hammer may be used to hammer the conductor casing into place. The conduct casing may go to depths of 40 to 300 ft depending on the location. The conductor casing is typically set through the top soil and loose rocks to the bed rock. The objective of the conductor casing is to isolate the wellbore from the top soil to ensure that loose debris does not enter the well during early drilling operations. The conductor casing is then cemented into place.
- Move-In and Rig Up (MIRU): Once the wellsite is prepared and the conductor casing is in-place, the rig is brought on location. Most land rigs, particularly those in North America, are transported on multiple trucks. Once on the well site or well pad, the rigging-up process begins. Rigging up the well consists of taking the rig modules from the trucks and assembling the rig. Included in the rigging up process is setting-up all of the rig systems and testing these systems. Here is a YouTube video, "Rigging up Land Drilling Rig" (3:35), showing the Rigging Up process of the derrick:
Pioneer Drilling 60 Series Rig-up Animation | Drilling Animation | Land Rig Animation | Oil & Gas. This video contains only background music with no words.Source: Industrial3D Inc | I3D [120].
Transporting and assembling the rig may take 50-75 workers (two crews), 35 – 40 vehicles, and take up to four days. If a multi-well pad is used, once the rig is rigged-up for the first well, then the rig can simply be skidded over to the next location without having to dig-down. - Spud the Well: After the rig has been inspected and all of the systems tested the well can be Spudded. Spudding a Well refers to starting the rotary drilling operations for that well.
- Drill Down to the Surface Casing Depth: The first section of the well to be drilled is the section that goes down to the pre-determined surface casing depth (Casing Point). Obviously, for this section of the wellbore, the drill bit diameter must be smaller than the ID (inner diameter) of the conductor casing. In this shallow section of the wellbore, fresh water aquifers (both for personal and municipal use) exist. As discussed earlier, shallow gas hazards may also exit. The objectives of drilling this first section of the well is to allow the setting and cementing of the surface casing to:
- protect the fresh water aquifers by placing a steel and concrete barrier to isolate the water table from the well;
- protect the well from the aquifer (cutting of the drilling fluids with fresh water);
- protect the well from shallow gas hazards.
- Run and Cement the Surface Casing: Once the surface casing point is reached, the surface casing is run into the wellbore and cemented into place. This process is performed by:
- Pulling Out of Hole (POOH): Tripping out of the hole with the drill pipe to remove it from the wellbore during cementing operations;
- running the surface casing;
- pumping a cement slurry down the interior of the casing;
- chasing the cement with drilling fluid to displace the cement up into the annular space between the casing string and the wellbore (rock);
- allowing time for the cement to Cure (harden).
The BOP is then installed on the surface casing string. - Continue this Process to Drill to the Next Casing Point: This drilling process is continued to the next pre-determined casing point. The selection of these intermediate-string casing points is beyond the scope of the class, but the criteria are based on the mud weight, the Fracture Pressure of the formations to be drilled (the pressure that causes the formation to fracture), the locations of any Lost Circulation Zones, and the locations of any High Pressure Zones. As we discussed earlier, any of these situations may result in a kick and a potential blowout. The objectives of the intermediate casing strings are:
- isolate unstable hole sections behind pipe;
- isolate lost circulation zones behind pipe;
- isolate under-pressured zones behind pipe (prevent lost circulation);
- isolate over-pressured zones behind pipe (prevent a kick);
- isolate multiple producing zones
- Continue this Process to Drill to each Casing Point: This process is repeated for each of the planned casing points. Obviously, as successive casing strings are run and cemented into place, smaller diameter tools and drill bits must be used for continued drilling operations. As we discussed earlier, the two most important drilling parameters within the Driller’s control to maximize the Rate of Penetration (ROP) of the drill bit are the weight-on-bit and the rotational speed of the rotary system in Revolutions per Minute (RPM).
- Continue this Process to Drill to Total Depth (TD): Once the final intermediate casing string is run and cemented, the drilling process is continued until the well reaches the TD (Total Depth) of the well. At this point, the well is said to be TD’ed.
- Log the Well with Open-Hole Logs: At this point, the sand face is exposed to the well and Open-Hole Logging Tools can be run in the well. Open-hole logs are used to measure certain properties of the subsurface formation that are of interest to the geologists and engineers working on the well and the reservoir.
- Run and Cement the Production Casing String or Liner: If a production casing string or production liner is to be used in the completion, then they are run and cemented at this time.
- Compete the Well: Install the well completion as discussed in earlier lessons:
- tubing
- gravel packs
- packers
- sliding sleeves
- stimulation
- acidize the well
- hydraulically fracture the well
- artificial lift
- Rig Down and Move Out

Finally, here is a YouTube video, "Drilling Animation" (5:58), showing the entire drilling process. This animation is from Chesapeake Energy, and it discusses the drilling process for a Marcellus Shale well:
9.4: Key Learnings
- There are five major systems on a modern rotary drilling rig:
- the Power System
- the Hoisting System
- the Circulation System
- the Rotary System
- the Well Control System (Blowout Prevention System)
- The power system is the system is the system that provides all power to the rig. On a modern rotary rig, this power is generated with the Prime Mover which is an electrical generator that is fueled with either diesel fuel or lease fuel. The electrical power is transmitted to the other systems and sub-systems on the rig by mechanical means (older rigs), direct current (DC), or alternating current (AC).
- The hoisting system is the system that does the heavy lifting on the rig. It is responsible for lifting drill pipe during tripping operations; and lifting and suspending the drill pipe during drilling operations, and lifting and installing the casing, tubing strings, and completion equipment into the well. In addition, the braking system on the hoisting system controls the weight-on-bit by taking up some of the load of the drill pipe.
- The circulation system of the drilling rig is responsible for circulating the drilling fluid from the mud pit to the drill bit and back. It is a continuous system of pumps, distribution lines, storage tanks, storage pits, and cleansing units that allows the drilling fluid to fulfill its primary objectives (these will be discussed later in this lesson). The main sub-systems of the circulation system are:
- the mud pit
- the mud pump
- the swivel
- the drill string
- the solids control system:
- the shale shaker
- the desander
- the desilter
- the degaser
- The drilling fluid itself is most often called mud. The drilling fluids discussed in these lesson notes are:
- water-based muds (WBM): mixtures of water, bentonite clay, and additives;
- oil-based muds (OBM): mixtures of with diesel oil, mineral oil, or synthetic oils as a continuous phase and water as a dispersed phase in an emulsion. In addition, additives such as emulsifiers and gelling agents are also used;
- foams: comparable to shaving cream; and
- air.
- Drilling fluids are critical in modern drilling operations. There are many objectives for using a drilling fluid. These include:
- lift drill cuttings from the bottom of the wellbore to the surface;
- suspend cuttings to prevent them from falling downhole if circulation is temporarily ceased;
- release the cuttings when they are brought to the surface;
- stabilize the borehole during drilling operations (exert hydrostatic or hydrodynamic pressure on the borehole to prevent rock caving into the wellbore);
- control formation pore pressures to assure desired well control (apply hydrostatic and hydrodynamic pressures in excess of the formation pore pressures to prevent fluids from entering the wellbore);
- deposit an impermeable filter cake onto the wellbore walls to further prevent fluids from permeable formations from entering the wellbore;
- minimize reservoir damage (assure low skin values) when drilling through the reservoir section of the well;
- cool the drill bit during drilling operations;
- lubricate the drill bit during drilling operations;
- allow for pressure signals from Logging While Drilling (LWD) or Measurement While Drilling (MWD) tools to be transmitted to the surface (LWD and MWD data are transmitted to the surface using pressure pulses in the drilling fluid);
- allow for pressure signals to be sent to the bottom of the well to pressure actuate certain downhole equipment;
- minimize environmental impact on subsurface natural aquifers.
- The rotary system of the drilling rig provides the torque for the drilling process. This torque is provided by the rotary table on a conventional rotatory rig or the top-drive unit on a top-drive rotary rig. This torque is conveyed through the drill pipe and the bottom-hole assembly to the drill bit.
- The lesson notes discussed three types of drill bits used on the drilling industry:
- milled-tooth tri-cone bit
- insert tri-cone bit
- fixed-cutter bit
- The drilling action of the tri-cone bits is due to an explosive gouging, crushing action; while the drilling action of the fixed-cutter bits are due to a scraping action.
- In a milled-tooth tri-cone bit, the teeth of the bit are milled from the same steel as the cone. Due to the grade of the steel used in the cones, the milled-tooth bits are typically used to drill through soft rock formations.
- In an insert tri-cone bit, the teeth inserts are made from stronger grades of steel than the cone. Typically, tungsten-carbide steel is used to create the teeth in an insert bit. The insert bits are used to drill through moderately hard formations or to extend the bit-life through soft formations.
- Fixed-cutter bits are bits that contain no moving parts. The cutters on fixed-cutter bits are typically polycrystalline (synthetic) diamonds which are used to form polycrystalline diamonds compact (PDC) bits. PDC bits are used to drill through hard rock formations.
- The Well Control System or the Blowout Prevention System is the system on a drilling rig that prevents the uncontrolled, catastrophic release of high-pressure fluids (oil, gas, or salt water) from subsurface formations. The well control system is comprised of:
- the Accumulator: stores compressed gas and compressed hydraulic fluids for the rig’s hydraulic systems;
- the Blowout Preventer: large stacked system of high-pressure valves that can be closed around or through drill pipe to isolate the subsurface formations from the rig.
- The well control system provides well control by:
- mud system: helps prevent kicks by exerting high hydrostatic and hydrodynamic pressures on the formations and depositing an impermeable mud cake across permeable formations;
- blowout preventer (BOP): helps to control a kick if one occurs.
- A kick is an unwanted but controllable entry of subsurface fluids into the wellbore; while a blowout is a catastrophic (usually) and uncontrollable entry of subsurface fluids into the wellbore. Blowouts can be catastrophic because of the combustible nature of hydrocarbons.
- The causes of a kick include:
- insufficient mud weight (density): the hydrostatic or hydrodynamic pressure exerted by the mud column is less than the formation pore pressure (the pressure is underbalanced);
- improper mud replacement during tripping: while tripping out of the hole mud volumes must be pumped into the wellbore at high enough rates to replace drill pipe being removed from the wellbore;
- swabbing: removing drill pipe from the wellbore can create a negative pressure (suction) if the drill pipe is removed too quickly;
- cut mud: if gas is entering the wellbore, then it may effectively reduce the wellbore pressure gradient;
- lost circulation: as discussed earlier if large volumes of drilling fluid enter the subsurface in (1) high permeability formations, natural fractures, or drilling-induced fractures, then the effect is a shortened height and weight of the mud column.
- The indicators/warning signs of a kick include:
- increase in the rate of flow of the drilling fluid returns at constant pump rates (primary indicator of a kick);
- volume of mud in the mud pit increases when no additional drilling fluids are added to the mud system (primary indicator of a kick);
- drilling fluids returns continue to flow when the mud pumps are turned off (primary indicator of a kick);
- improper wellbore fill-up/volume-balance on trips (primary indicator of a kick);
- pump pressure decrease and pump stroke increase (secondary indicator of a kick);
- change in the apparent weight-on-bit (secondary indicator of a kick);
- occurrence of a Drill Break or Bit Drop (secondary indicator of a kick);
- reduction in the mud weight (secondary indicator of a kick).
- The drilling company and operating company will always have a detailed, well-specific procedure in place in the advent of a kick.
- All wells are drilled with a set sequence of operations.
9.5: Summary and Final Tasks
Summary
We began this lesson by discussing the five major systems on a modern rotary drilling rig. These are:
- the Power System
- the Hoisting System
- the Circulation System
- the Rotary System
- the Well Control System (Blowout Prevention System)
We discussed each of these systems along with the more important sub-systems that comprise these systems.
The power system on a drilling rig provides the for the other main systems on the rig and other ancillary systems, such as electrical systems, pumps, etc. The system typically consists of a prime mover (the component of the power system that generates the raw power) and a means to transmit the raw power to the end-use components on the rig. The sub-systems of the power system that were discussed in detail or listed and shown in Figure 9.02 include:
- the Fuel Storage
- the Engines and Generators
- means of power transmission
- mechanical
- direct current
- alternating current
The hoisting system on a drilling rig does the heavy lifting on the rig. It is used to raise, lower, and suspend the drill string and lift casing and tubing for installation into the well. The sub-systems of the hoisting system that were discussed in detail or listed and shown in Figure 9.02 include:
- the Crown Block
- the Mast/Derrick
- the Monkey Board
- the Traveling Block
- the Hook
- the Swivel
- the Drawworks
- the Weight Indicator
- the Drilling Line
The circulation system on a drilling rig allows for circulation of the Drilling Fluid or Mud down through the hollow drill string and up through the annular space between the drill string and wellbore. It is a continuous system of pumps, distribution lines, storage tanks, storage pits, and cleansing units that allows the drilling fluid to fulfill its primary objectives. The sub-systems of the circulation system that were discussed in detail or listed and shown in Figure 9.02 include:
- the Swivel
- the Rotary Hose
- the Mud Return Line
- the Shale Shaker
- the Choke Manifold
- the Mud Gas Separator
- the Degasser
- the Reserve Pit
- the Mud Pits
- the Desander
- the Desilter
- the Mud Pumps
- the Mud Discharge Line
- the Bulk Mud Components Storage
- the Mud House
- the Water Tank
The drilling fluid (mud) is a critical part of the drilling process. Muds can be water-based fluids, oil-based fluids, foam, or air. The objectives/functions of the mud are:
- lift drill cuttings from the bottom of the wellbore to the surface;
- suspend cuttings to prevent them from falling downhole if circulation is temporarily ceased;
- release the cuttings when they are brought to the surface;
- stabilize the borehole during drilling operations (exert hydrostatic or hydrodynamic pressure on the borehole to prevent rock caving into the wellbore);
- control formation pore pressures to assure desired well control (apply hydrostatic and hydrodynamic pressures in excess of the formation pore pressures to prevent fluids from entering the wellbore);
- deposit an impermeable filter cake onto the wellbore walls to further prevent fluids from permeable formations from entering the wellbore;
- minimize reservoir damage (assure low skin values) when drilling through the reservoir section of the well;
- cool the drill bit during drilling operations;
- lubricate the drill bit during drilling operations;
- allow for pressure signals from Logging While Drilling (LWD) or Measurement While Drilling (MWD) tools to be transmitted to the surface (LWD and MWD data are transmitted to the surface using pressure pulses in the drilling fluid);
- allow for pressure signals to be sent to the bottom of the well to pressure actuate certain downhole equipment;
- minimize environmental impact on subsurface natural aquifers.
The rotary system on a drilling rig is the system that causes the drill bit rotate at the bottom of wellbore. We have discussed some components of the rotary system when we discussed rotary table and top-drive rigs, but we have not yet discussed the entire system. The sub-systems of the rotary system that were discussed in detail or listed and shown in Figure 9.02 include:
- the Swivel
- the Kelly or (Top-Drive Unit on a top-drive rig)
- the Kelly Bushing or (Top-Drive Unit on a top-drive rig)
- the Master Bushing or (Top-Drive Unit on a top-drive rig)
- the Rotary Table or (Top-Drive Unit on a top-drive rig)
- the Mousehole
- the Rat Hole
- the Rotary Hose
- the Drill String
- the Bottom-Hole Assembly
- the Drill Bit
Drill bits come in different shapes and sizes. The choice of the appropriate bit depends on the formations to be drilled. The drill bits that we discussed in this lesson include:
- milled-tooth tri-cone bit (for drilling through soft rock formations)
- insert tri-cone bit (for drilling through medium to hard rock formations)
- fixed-cutter bit (for drilling through hard rock formations)
The well control system or the blowout prevention system on a drilling rig prevents the uncontrolled, catastrophic release of high-pressure fluids (oil, gas, or salt water) from subsurface formations. The sub-systems of the well control system that were discussed in detail or listed and shown in Figure 9.02 include:
- the Accumulator
- the Blowout Preventer
A kick is an unwanted but controllable entry of subsurface fluids into the wellbore; while a blowout is a catastrophic (usually) and uncontrollable entry of subsurface fluids into the wellbore. Blowouts can be catastrophic because of the volatile, combustible nature of hydrocarbons.
The causes of a kick include:
- insufficient mud weight (density): the hydrostatic or hydrodynamic pressure exerted by the mud column is less than the formation pore pressure (the pressure is underbalanced);
- improper mud replacement during tripping: while tripping out of the hole mud volumes must be pumped into the wellbore at high enough rates to replace drill pipe being removed from the wellbore;
- swabbing: removing drill pipe from the wellbore can create a negative pressure (suction) if the drill pipe is removed too quickly;
- cut mud: if gas is entering the wellbore, then it may effectively reduce the wellbore pressure gradient;
- lost circulation: as discussed earlier, if large volumes of drilling fluid enter the subsurface in (1) high permeability formations, natural fractures, or drilling-induced fractures, then the effect is a shortened height and weight of the mud column.
The indicators/warning signs of a kick include:
- increase in the rate of flow of the drilling fluid returns at constant pump rates (primary indicator of a kick);
- volume of mud in the mud pit increases when no additional drilling fluids are added to the mud system (primary indicator of a kick);
- drilling fluids returns continue to flow when the mud pumps are turned off (primary indicator of a kick);
- improper wellbore fill-up/volume-balance on trips (primary indicator of a kick);
- pump pressure decrease and pump stroke increase (secondary indicator of a kick);
- change in the apparent weight-on-bit (secondary indicator of a kick);
- occurrence of a Drill Break or Bit Drop (secondary indicator of a kick);
- reduction in the mud weight (secondary indicator of a kick).
Safety is of the utmost importance in the oil and gas industry, and detailed well procedures are developed for each well. In addition, daily safety meetings discussing the status of the well, the day’s operations, and the safety concerns for that day’s operations are typically performed by all responsible drilling companies and operating companies.
Finally, we discussed the steps in the drilling procedure (Making Hole). An oil or gas well is drilled in a very ordered sequence. The steps in this sequence are almost universally applied to the drilling of all wells. These include:
- plan the Well
- perform Shallow Gas Survey
- prepare the Wellsite
- Set the Conductor Casing
- Move-In and Rig Up
- Spud the Well
- Drill Down to the Surface Casing Depth
- Run and Cement the Surface Casing
- Continue this Process to Drill to the Next Casing Point
- Continue this Process to Drill to each Casing Point
- Continue this Process to Drill to Total Depth (TD)
- Log the Well with Open-Hole Logs
- Run and Cement the Production Casing String or Liner (if part of the completion design)
- Compete the Well – install the well completion:
- Tubing
- Gravel packs
- Packers
- Sliding sleeves
- Stimulation
- Acidize the well
- Hydraulically fracture the well
- Artificial lift
- Rig Down and Move Out
Final Tasks
Complete all of the Lesson 9 tasks!
You have reached the end of Lesson 9! Double-check the to-do list on the Lesson 9 Overview page [121] to make sure you have completed all of the activities listed there before you begin the Final Exam Review week.








