Click here for a transcript.
Hello and welcome to this new lesson on confidence intervals. Before we get into confidence intervals, we're going to talk about sampling distributions. Because we ultimately perform the confidence interval on the sampling distribution. So we need to talk about how we actually get those sampling distributions. And so, in this video series, we're going to be using some simulated dice rolls. And so, you can imagine a situation in which you roll two dice, you take the total, and then you record that total. And ultimately we did this four times, but 10 rules in each time. So, we've got four different samples of 10 data points. So with that, let's go ahead and jump in to the video.
So, we are here in Google Codelab. We're going to be using two main libraries in this series of videos. The first is going to be pandas and the second is plot nine. And then, as I mentioned, we're going to go over sampling distributions. So I went ahead and preloaded this sampling data and as I mentioned we've got four samples here, and we've got 10 dice rolls in each sample, and we recorded the total. What we're actually doing here with these curly brackets is essentially creating a dictionary and then converting it in to a data frame right away. So if you recall in lesson one, we talked about dictionaries and data frames and how we can convert between the two. Here we're just doing it all in one step. So we've got our data underscore DF for data frame. however, we're going to convert this into a long form data frames, which will allow us to help with plotting down the line. So we're going to be using that melt command that we talked about in lesson three.
So, I'm just going to rename override the data DF name and say data df dot melt. And then, we need to give it our value vars. So, which values do we want to maintain and in this case we want to maintain sample One, sample two. Each of these samples is a column, so we want to keep them as they are. So those are going to be our value vars and I forgot an equal sign, right there, and then we also need to give it a var name. So what do we want these new values to be called? We'll call them sample, and we give it a value name. What do we want what's in them could be called? And we'll call that outcome.
And so then I'll just print the data frame. We'll just show the first five rows using this dot head command. And so we can see here we've got our sample, and we've got our outcomes. And so, we can use this to create plots. And so, as we talked about in lesson three, it's often a lot easier to plot using this long form, especially when we're working with gg plot. So our first visualization is to just look at how these different samples relate, and so we're going to do a histogram with filled bars. So we're going to have our basic histogram, and then we're going to add a variable using the fill command. So I'll start with the gg plot command. So we say gg plot data underscore DF.
And then we give our geom. So geom underscore histogram and then we give our AES. So this is the requirement. So we need an x value which we will call, which will plot our outcome so our actual dice rolls. And then, it's a histogram, so we don't need a y value because it's just going to give us the count. But we will add a fill based off of sample within the AES statement because we want to attach it to a variable. And then I'm going to specify that I want 12 bins we want one bin per possible dice roll and I want each of those bins to be one long. So if we run this, we can see our plot here. We've got each of our samples has been automatically put into a legend. And then we can see sort of the distribution and because we've done fill. It's stacked each of these samples on top of each other, so we can see as the whole group of samples. All 40 data points that we ran. The most common was seven across all the samples. And it does tend to follow you know vaguely normal distribution. But we can see that, for example, sample 4 was heavily skewed towards the lower values. It looks like sample two and three might have more of the higher values, and so we do see that there are differences there between our samples. So this is just a good way to get an idea about what your samples exist.
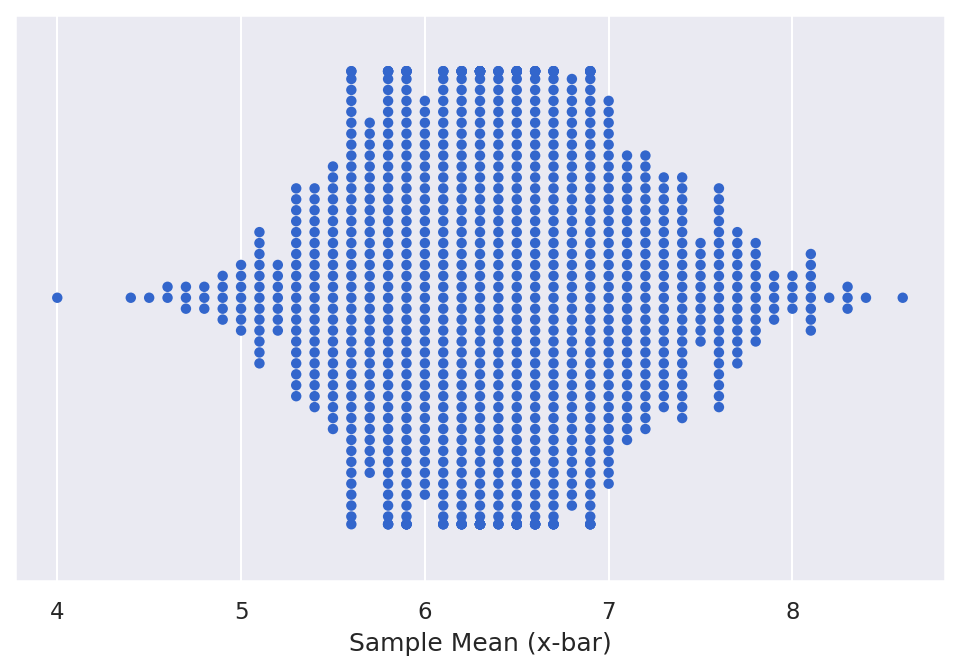
But we still need to determine the sampling distribution. And so we have two steps to determine the sampling distribution. The first is to find the mean of each sample, and then we're going to plot it. So the sampling distribution is the distribution of statistics, and in this case we're going to say x bar is our statistic. So we need to first find the mean of each sample. So we say data means, and we are going to use a group by function. So we want to group by sample. So we want to group first we're going to group by sample. Then we're going to take the mean of each of those rows in the now grouped sample. And then we're going to tag on a rename function. So here we just will rename our outcome column to sample means. Which just is a little bit more descriptive because it'll no longer be the outcome. It'll be the means of the outcome. So we can print that and in theory you can do each of these steps individually. But one of the benefits of working with pandas, is that you can just sort of tag on these additional commands using this period or dot right here. So we can do dot group by dot mean dot rename, and it'll integrate them all in order. So if we print this, we can now see our sample means here. So we've got sample one with a mean of six, sample two 6.3, 7.5, and 5.7. So this is our sampling distribution, it's our sample means or distribution of the sample means. To visualize that, we'll often use what's called a Dot Plot, and so it will function very similarly to a histogram. But we'll start with just plotting data means. And now the geom is geom dot plot. It still requires an AES.
Here we want our sample means. There's no other data that we're doing. We're not adding a fill. No need to specify any y-axis, but normally we will specify the dot size. Just so that the dots don't overwhelm the plot, and so here we can see that it's plotted a single dot for each of our sample means. But it stacked them into bins the way that a histogram would. And so you can use this as a way to see the distribution of data the way you would a histogram, but you can also see how frequently a certain points are. Where they are each located and if we wanted to we can add additional variables to show the fill. To show lines that can make this a bit more descriptive. So with that, this is how we can create a sampling distribution from a small subset of samples.
 Read It: Sampling Distributions
Read It: Sampling Distributions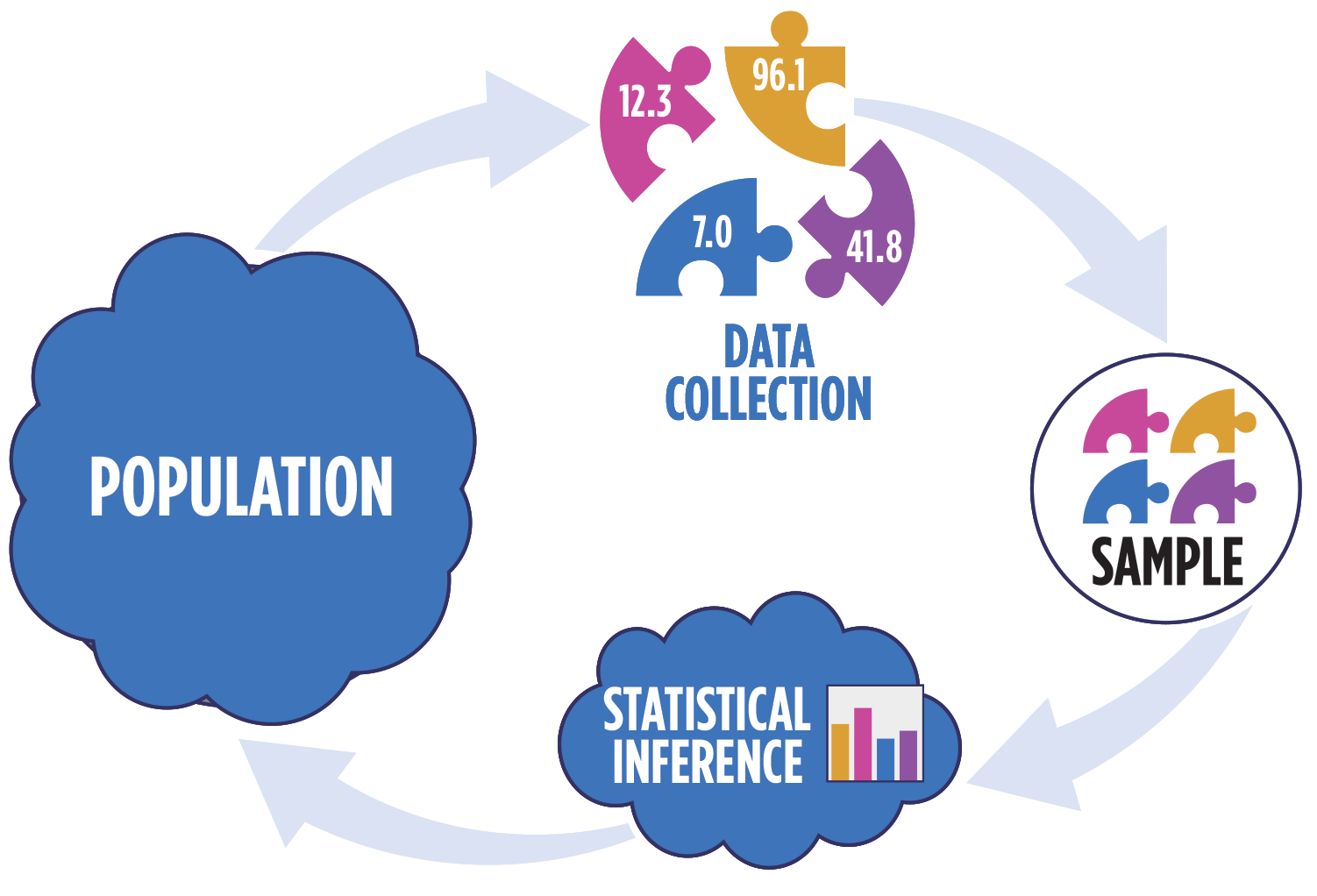
 Watch It: Video - Introduction to Sampling Distributions (10:33 minutes)
Watch It: Video - Introduction to Sampling Distributions (10:33 minutes) Watch It: Video - Comparing Samples to Population (13:51 minutes)
Watch It: Video - Comparing Samples to Population (13:51 minutes) Try It: Apply Your Coding Skills in Google Colab
Try It: Apply Your Coding Skills in Google Colab Assess It: Check Your Knowledge
Assess It: Check Your Knowledge FAQ
FAQ