 Read It: Measures of Spread: Standard Deviation
Read It: Measures of Spread: Standard Deviation
In addition to knowing the center of a distribution of data values, it is often useful to know how dispersed or spread-out the distribution it. A common measure of this spread is the standard deviation:
Standard Deviation: the typical distance of a data value from the mean.
A larger standard deviation indicates a more dispersed collection of values, whereas a smaller standard deviation indicates a narrower distribution. To make the interpretation of the standard deviation more quantitative: a new, randomly drawn value from the population will have a 95% chance of being within the range -2 to +2 standard deviations from the mean (i.e., ). This is depicted in the example image below.
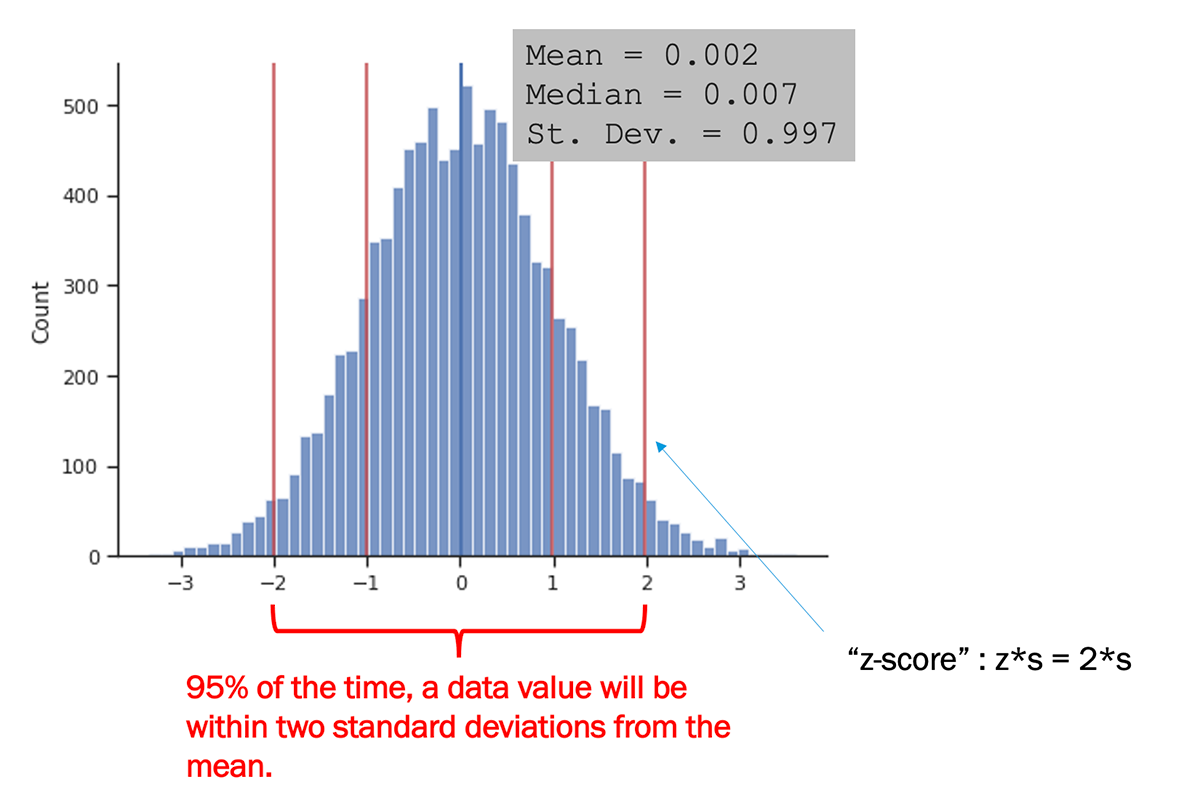
The image above also introduces the z-score, which we will come back to later in the course. The z-score, , is simply the number (or fraction) of standard deviations that a value is from the mean. The z-score can be reported for a data point, or for a hypothetical value, such as the far right red line in the example above (where ).
A Note on Notation
The formula above gives the standard deviation for a sample, noted s. The standard deviation for the entire population is noted with (or "sigma", a Greek letter).
 Watch It: Video - Measures of Spread (4:36 minutes)
Watch It: Video - Measures of Spread (4:36 minutes)
The above video demonstrates how to calculate standard deviation using the std function from Pandas. There is also a std function from Numpy, however in order to use that function to calculate standard deviation as given in the above formula, you need to specify the argument ddof=1 to represent the 1 being subtracted from n in the denominator:
1 | numpy.std(x, ddof=1) |
where x is an array of values.
 Try It: DataCamp - Find the standard deviation
Try It: DataCamp - Find the standard deviation
You already found the mean and median of the total electricity consumed in a year (KHW) in the previous page.
| HOME ID | DIVISION | KWH |
|---|---|---|
| 10460 | Pacific | 3491.900 |
| 10787 | East North Central | 6195.942 |
| 11055 | Mountain North | 6976.000 |
| 14870 | Pacific | 10979.658 |
| 12200 | Mountain South | 19472.628 |
| 12228 | South Atlantic | 23645.160 |
| 10934 | East South Central | 19123.754 |
| 10731 | Middle Atlantic | 3982.231 |
| 13623 | East North Central | 9457.710 |
| 12524 | Pacific | 15199.859 |
* Data Source: Residential Energy Consumption Survey (RECS)(link is external), U.S. Energy Information Administration (accessed Nov. 15th, 2021)
Now can you find the standard deviation using Python?
 Assess It: Check Your Knowledge
Assess It: Check Your Knowledge
Use the table below to answer the following questions.
| Make | Model | Type | City MPG |
|---|---|---|---|
| Audi | A4 | Sport | 18 |
| BMW | X1 | SUV | 17 |
| Chevy | Tahoe | SUV | 10 |
| Chevy | Camaro | Sport | 13 |
| Honda | Odyssey | Minivan | 14 |
 FAQ
FAQ