Hypothesis Test for Single Mean

If you have a single sample, and are concerned with showing that its mean is significantly larger or smaller than some value (which will be the null value), then you want to perform a "single mean test".

Read It: Hypothesis Test for Single Mean

In a single mean test, your statistical hypotheses will take the following form, and your statistic, computed on both the original sample and the randomized samples, is $\bar{x}$ :

Test	Hypotheses	Statistic	Randomization Procedure
Single Mean	$H_{o} : μ = null value$ $H_{a} : μ < null value or μ > null value$ or $μ \neq null value$	Sample mean, $\bar{x}$	Shift sample so that mean agrees with null value

The null value will typically be some threshold or standard that you are comparing your sample mean against. Going back to the PM2.5 example earlier in this lesson, the null value for that single mean test is 12.5 micrograms per cubic meter.

Randomization Procedure

The randomization procedure that we will use for a test of a single mean involves shifting all the values in the original sample by a uniform amount, such that the resulting sample mean equals the null value, $μ$ . The amount to shift all values by is the difference between $μ$ and the original sample mean, $\bar{x}$ . The pseudo-code for this procedure is:

Obtain a sample of size n
Calculate: $x_{s} = x + (μ - \overset{―}{x})$
For i in 1, 2, ..., N
1. Randomly draw a new sample, of size n, with replacement from the shifted sample, $x_{s}$ .
2. Calculate the sample mean for this new randomized sample
3. Store this value as the ith randomized statistic
Combine all N randomized statistics into the randomization distribution

Random drawing of values with replacement allows for the possibility of values being drawn more than once, and with equal probability each time.

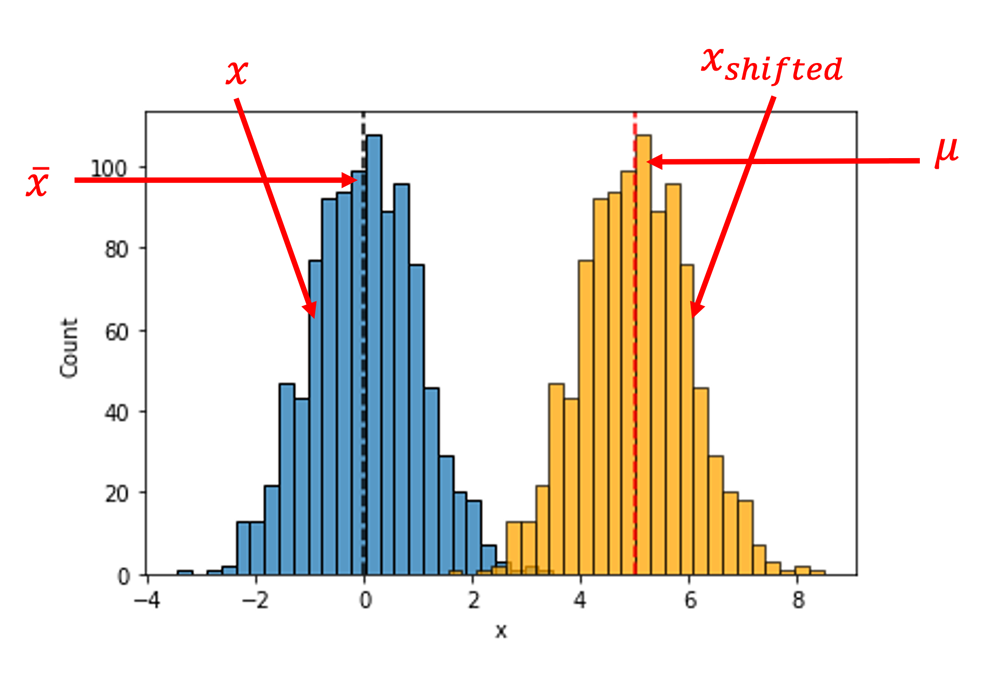
The figure below provides an example of this randomization procedure. The blue histogram represents the original sample data, centered at $\bar{x}$ , and the yellow histogram depicts the shifted sample which is now centered at the null value, $μ$ . Note that the two histograms share the exact same shape, and thus the same spread.

Enter image and alt text here. No sizes!

Example of this randomization procedure

Credit: © Penn State is licensed under CC BY-NC-SA 4.0

The following video demonstrates how to implement this procedure in Python, using the 2021 Texas Power Crisis as an example.

Watch It: Video - Hypothesis Test for Single Mean (15:34 minutes)

Click here for a transcript.

All right, in this series of videos we're going to shift back into hypothesis testing. And in particular, we're going to focus on the one-line tests that you can do to do all of the hypothesis testing that we learned in the previous lesson, but in just a single line. And while a lot of times we'll still want to do the randomization procedures, these one-line tests can be a good way to to check your answer. Because although they may be slightly different, a lot of times they should actually follow the same pattern as your randomization distribution. So, let's go ahead and jump right in. So, we're here in the code for hypothesis testing. And in particular, I'm going to focus on the hypothesis test for a single mean in this video.

And so, when we write our hypotheses, we say that mu equals in this case 6.1, the capacity. And then our alternative is that mu is less than that. So in essence, we're going to test whether or not wind actually met the capacity in, during the Texas 2021 cold snap. And so, in the previous lesson we went through these steps: we shifted the data, we initialized the variable, and we implemented this randomized random choice function where we set replace equal to true and focused on the shifted data. And then, eventually we calculated the p-value as the proportion of data that was less than our original mean. And we got a p-value of zero, which leads us to reject the null hypothesis in favor of the alternative, that the capacity of wind, that the average wind was less than the capacity. And so, this one-liner test, we're going to use a library, the stats library in Python. And in particular, this library is the stat SCI Pi stats, which is the same library that we used when we were writing our normal or working with the normal distributions in the previous videos.

And so, in order to do the single mean hypothesis test, I'm going to put the results into a variable called results. And we say stats dot ttest underscore one - the number one - samp. So effectively, a one sample ttest. Then we give it our data, which is wind - which is the observed wind generation. We give it our population mean, which is what we expect. So this is our capacity in this case, or whatever value you have set in the null hypothesis. And then we give it the alternative. And in this case, we specify the alternative as less. Meaning that we are doing a test in which we're looking at less than, we're using a left-tailed test. And then to actually see the p-value we can just say results dot p-value at the end. And so, we can run this. And we can see that the p-value is still less than our significance level. It's very, very close to zero. But as what often happens in these one-liner tests, that is more specific. So, instead of just staying zero, we've got you know quite a few digits, but still very, very, very close to zero given the e to the negative seven. And this is a very common result when we're using these one-liners and comparing them to randomization procedures, because what this one-liner test is actually doing is conducting that same randomization procedure that we went over, but with a lot more data. And so, essentially, it does something very similar to this. And instead of being a thousand, is maybe a million, 10 million. It essentially generates a lot more iterations, which allow it to become a lot more specific in the results.

The Google Colab Notebook use in the above video is available here(link is external), and the data are here(link is external). For the Colab file, remember to click "File" then "Save a copy in Drive". For the data, it is recommended to save to your Google Drive.

Try It: Tesla Range Scandal

A class-action lawsuit(link is external), filed August 2nd, 2023, essentially alleges that Tesla, the electric vehicle company, grossly exaggerated the ranges on some of its vehicles. Plaintiffs claim that the rated ranges on their Tesla cars are much larger than actual ranges they get under normal driving conditions. The lawsuit includes several Tesla models, one of which being the Model S. Plug In America collects self-reported survey data on EV performance, including the Model S(link is external). In this example, we'll look at the 70 kWh, dual motor ("70D") version of the Model S, with a rated range of 240 miles. We will exclude any cars with more than 10,000 miles on the odometer. As of this writing, the dataset includes a sample of 5 of these cars.

Our question here is "Do the actual ranges of the Model S 70D fall significantly below the rated range of 240 miles?" Our hypothesis could be: "Yes, they do fall below." Thus, our statistical hypotheses are:

$H_{o} : μ = 240 m i l e s$
$H_{a} : μ < 240 m i l e s$

Develop Python code below to test these hypotheses, and calculate a p-value. The knowledge check will then ask about the conclusion of this test.

Hypothesis Test for Single Mean